-
摘要: 为了探讨无限弹性土体内圆柱形洞室在突加反平面冲击荷载作用下的瞬态响应,利用Laplace变换及围道积分逆变换,得到土体位移和应力的一般解析表达式,并给出了数值解。在时域内分析了无限弹性土体内圆柱形孔洞在轴向荷载作用下的动力响应,并将计算结果与采用拉普拉斯数值反变换得到的结果以及静力情况下的结果作了比较。研究结果显示:波到达后,该点土体的应力和位移均瞬间增大,随后慢慢减小,并逐渐趋于静力值;波向外发散传播,并沿半径方向衰减,衰减速度比静力情况的应力衰减慢。Abstract: To explore the transient response of a cylindrical cavity in an infinite elastic soil body to sudden anti -plane impact, the general analytical expressions were given for the displacement and stress of the soil, respectively, by using the Laplace transform.And the corresponding numerical solutions were presented.In the time domain, the dynamic responses of the infinite elastic soil to the impact load along the axial of the cavity were analyzed, and the computed results were compared with those from the numerical inversion proposed by Durbin and the static results.And there are some understandings of shear wave propagation as follows: the stress and displacement of the soil can increase instantaneously when the shear wave arrives here, then decrease gradually and tend to the static values; the shear wave spreads outward and attenuates along the radial directions, the attenuation rate is lower than that under static conditions.
-
Key words:
- solid mechanics /
- dynamic responses /
- Laplace transform /
- cylindrical cavity /
- anti -plane /
- impact load
-
深埋洞室常用于地下隧道、流体运输。随着地下交通的发展, 地下洞室在外力作用下的动力响应成为诸多领域的重要课题之一。相关研究者[1-5]利用波函数展开法、积分变换和数值方法等研究了圆柱形洞室对波的散射和衍射。然而, 洞室表面受到突加荷载作用而引起的波的传播问题越来越引起注意。G.Eason[6-7]、张庆元等[8]和刘国利等[9]运用Laplace变换及其逆变换, 得到了球形空腔及圆柱形洞室表面受均匀且仅为时间的函数的外力作用所引起的弹性波的传播规律及动力响应; H.Herman等[10]、T.L.Geers[11]和杨俊等[12]基于积分变换研究了无限长圆柱形壳体在突加压力作用下的瞬态动力响应; M.J.Forrestal等[13]求得了内源Heaviside荷载作用下, 以初等函数形式表示的流体介质中无限长弹性柱壳动力响应的精确解; T.B.Moodie等[14-15]运用积分变换及数值方法, 研究了圆柱形洞室表面受突加外荷载作用时膨胀波的传播, 得到了渐进的波震面展开式; N.Akkas等[16], U.Zakout等[17]运用残余变量法将二阶扩散方程降为一阶, 得到了Heaviside荷载作用下, 不同模态下圆柱孔洞的表面位移; V.R.Feldgun等[18]采用变分差分的方法研究了内爆炸荷载作用下球形和圆柱形孔洞动力响应问题, 分析了弹性波在壳体和土体中的传播; 高盟等[19-20]和蔡袁强等[21]采用拉普拉斯变换, 得到圆柱形孔洞在内源荷载作用下的动力响应问题, 并运用逆拉普拉斯变换的数值方法, 给出了问题的数值解。
上述研究均是圆柱形或球形洞室表面受到突加的径向外力作用而引起的膨胀波的传播, 对洞室表面受轴向力作用下引起的剪切波的传播的影响比较少。J.B.Haddow等[22-23]用数值的方法研究了非线性轴向剪切波的传播, 分析了洞室表面剪切应力引起的有限振幅方位剪切波的传播; K.Watanabe等[24]研究了圆柱形各向异性固体在点源SH波入射下的瞬态响应, 得到了任意圆柱形各向异性体的一般解决办法; D.W.Barclay[25-27]采用波震面展开的方法研究了圆柱形洞室表面在轴向剪切应力的作用下轴向剪切波传播, 得到了近似的解析解答。由于数学分析上的困难, 对剪切波传播的研究都是基于数值方法或是半解析的, 但是解析解答仍然非常必要。
本文中, 将列车急刹车时对隧道产生的冲击简化为无限弹性体中施加在圆柱形洞室表面沿轴线方向的均布荷载, 利用Laplace变换, 讨论无限弹性土体内圆柱形孔洞在轴线方向冲击荷载的作用下的瞬态响应, 采用围道积分[1]进行Laplace逆变换, 求解土体位移和应力的一般解析表达式, 并将计算结果与静力情况下的响应和采用F.Durbin[28]提出的拉普拉斯数值逆变换得出的结果进行比较。
1. 计算模型与求解
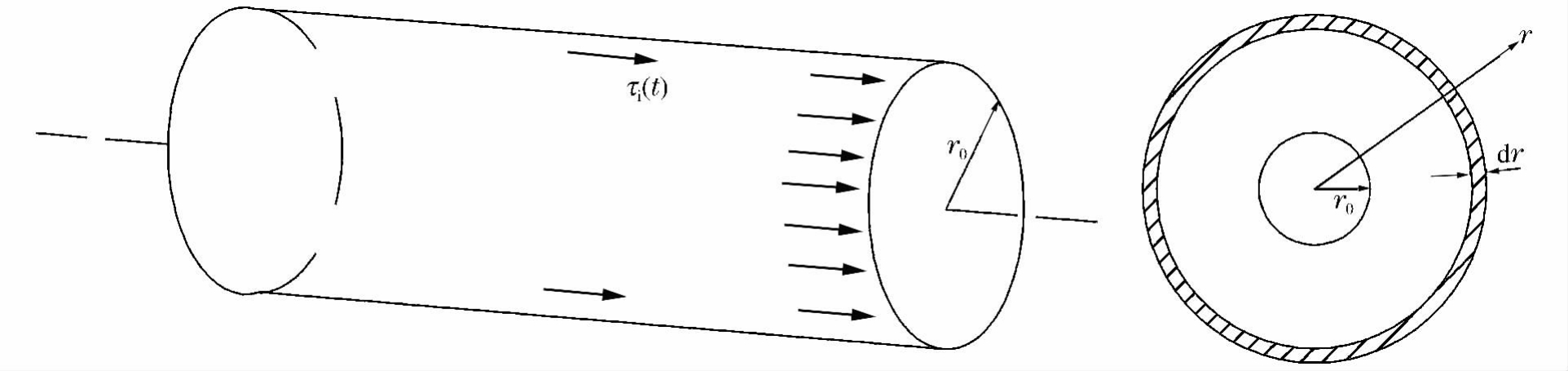
将土体视为无限弹性匀质各向同性材料。地下洞室受到刹车荷载力, 荷载先传递给衬砌, 再由衬砌传递给外部土体, 衬砌的模量远大于土体的模量, 因此可以认为冲击通过衬砌均匀地传递给外部土体, 列车急刹车时对洞室产生的冲击近似沿轴线方向的均布荷载。该问题简化为无限空间弹性土体中一半径为r0的无限长圆柱形孔洞内部有一沿洞室轴线方向的均布突加荷载τi(t), 如图 1所示。
1.1 控制方程
作为反平面问题, 以位移表示的控制方程为:
∂2w(r,t)∂r2+1r∂w(r,t)∂r=1v2s∂2w(r,t)∂t2 (1) 式中:r为土体中一点到洞室圆心的距离, w(r, t)为土体的轴线方向的位移, vs为剪切波在弹性土体中的传播速度, vs=(G/ρs)1/2, G为材料的Lame常数, ρs为土体的密度。
1.2 边界条件和初始条件
该问题中, 应满足在无穷远处应力为0, 因此应力τ满足边界条件:
{τ=τi(t)r=r0τ=0r=∞ (2) 初始时刻, 土体的位移和速度均应为0, 因此有初始条件:
{w(r,t)=0t=0∂w(r,t)∂t=0t=0 (3) 1.3 求解频域解
式(1)中同时含有空间变量r和时间变量t, 边界条件(3)中包含时间函数τi(t), 在物理平面上不易求解。利用Laplace变换法, 可将式(1)写为:
∂2W(r,s)∂r2+1r∂W(r,s)∂r=s2v2sW(r,s) (4) 式中:W(r, s)为w(r, t)关于t的Laplace变换, 记为W(r, s)=L[w(r, t)], s为变换参数, s=a+ib, a为任意正值, 且a > Re W。式(4)为零阶虚宗量的Bessel方程, 令k=s/vs, 则式(4)的通解[29]为:
W(r,s)=C1(s)I0(kr)+C2(s)K0(kr) (5) 式中:I0(kr)、K0(kr)分别为第一类和第二类零阶虚宗量Bessel函数, C1(s)、C2(s)为待定系数, 由虚宗量Bessel函数的渐近性质与递推关系[29], 可知C1(s)=0。
以Heaviside荷载为例, τi(t)=τ0H(t)(其中H(x)为Heaviside函数), L[τi(t)]=τ0/s。经Laplace变换后, 结合应力位移关系, 式(2)变为:
∂W(r,s)∂r=τ0Gs (6) 结合(5)式可得, 未知系数C2(s)=τ0/[ksGK1(kr0)], K1(kr0)为第二类一阶虚宗量Bessel函数。
由以上得到无限弹性土体中圆柱形孔洞反平面内源问题的频域表达式:
{W(r,s)=−τ0vsGs2K0(sr/vs)K1(sr0/vs)T(r,s)=τ0sK1(kr)K1(kr0) (7) 式中:Τ(r, s)=L[τ(r, t)]。
1.4 解析法求解时域解
为了在物理空间内获得时域解, 须对频域解施以Laplace逆变换, 记:
{D(ζ)=K0(ζr/r0)ζ2K1(ζ)eζγE(ζ)=K1(ζr/r0)ζK1(ζ)eζγ (8) 式中:ζ=kr0, γ=vst/r0。为了计算式(7)的Laplace逆变换, 要选择合适的积分路线。考察D(ζ)和E(ζ)的奇异性可知, ζ=0是D(ζ)和E(ζ)的支点, 另外I0(kr)和K0(kr)没有零点, 因此采用围道积分的方法计算式(7)的积分。图 2给出了所选取的积分围道, 其中L1和L5为半径无穷大的圆弧, L3为半径趋于0的圆, L2和L4为分支割线。
在积分围道内部, D(ζ)和E(ζ)是解析的, 由留数定理知:
(9) 式中:
 和
和 分别为D(ζ)和E(ζ)的留数。
分别为D(ζ)和E(ζ)的留数。
可以证明[1]:
∫L1+L5D(ζ)dζ=0,∫L1+L5E(ζ)dζ=0 (10) 沿L3计算积分。ζ=ρeiθ。应用虚宗量Bessel函数的近似公式[30], 当ρ→0时, K0(ζ)~-ln(ζ/2), K1(ζ)~1/ζ。根据留数定理[29], D(ζ)和E(ζ)沿L3的积分可以写成:
{∫L3D(ζ)dζ∼−∫L3ln(rζ/2r0)ζeξγdζ=−2πilim (11) 计算D(ζ)和E(ζ)沿分支割线L2和L4的积分。沿L2和L4, ζ=ρe±iπ=-ξ, 对于ρ > 0, Kν(-ξ)=(-1)-νKν(ξ)∓iπIν(ξ)[1], 其中Kν(ξ)和Iν(ξ)为ν阶虚宗量贝赛尔函数。由此得到:
\left\{\begin{array}{l} \int_{L_{2}+L_{4}} D(\zeta) \mathrm{d} \zeta=\int_{0}^{-\infty} \frac{2 \pi \mathrm{i}\left[K_{1}(\xi) I_{0}\left(\xi r / r_{0}\right)+K_{0}\left(\xi r / r_{0}\right) I_{1}(\xi)\right]}{\xi^{2}\left[K_{1}^{2}(\xi)+\pi^{2} I_{1}^{2}(\xi)\right]} \mathrm{e}^{-\xi \gamma} \mathrm{d} \xi \\ \int_{L_{2}+L_{4}} E(\zeta) \mathrm{d} \zeta=\int_{0}^{+\infty} \frac{2 \pi \mathrm{i}\left[K_{1}(\xi) I_{0}\left(\xi r / r_{0}\right)-K_{1}\left(\xi r / r_{0}\right) I_{1}(\xi)\right]}{\xi\left[K_{1}^{2}(\xi)+\pi^{2} I_{1}^{2}(\xi)\right]} \mathrm{e}^{-\xi \gamma} \mathrm{d} \xi \end{array}\right. (12) 根据式(9)~(12)可以得到时域内土体位移和应力的解析表达式:
\left\{\begin{aligned} w(r, t)=& -\frac{\tau_{0} r_{0}}{G} \int_{0}^{+\infty} \frac{\left[K_{0}\left(\xi(r+\delta r) / r_{0}\right)-K_{0}\left(\xi r / r_{0}\right)\right] I_{1}(\xi)}{\xi^{2}\left[K_{1}^{2}(\xi)+\pi^{2} I_{1}^{2}(\xi)\right]} \mathrm{e}^{\xi v_{s} t / r_{0}} \mathrm{~d} \xi-\\ & \frac{\tau_{0} r_{0}}{G} \int_{0}^{+\infty} \frac{K_{1}(\xi)\left[I_{0}\left(\xi(r+\delta r) / r_{0}\right)-I_{0}\left(\xi r / r_{0}\right)\right]}{\xi^{2}\left[K_{1}^{2}(\xi)+\pi^{2} I_{1}^{2}(\xi)\right]} \mathrm{e}^{\xi v_{s} t / r_{0}} \mathrm{~d} \xi+\frac{\tau_{0} r_{0}}{G} \ln \frac{r+\delta r}{r} \\ \tau(r, t)=& \tau_{0} \int_{0}^{+\infty} \frac{K_{1}(\xi) I_{1}\left(\xi r / r_{0}\right)-K_{1}\left(\xi r / r_{0}\right) I_{1}(\xi)}{\xi\left[K_{1}^{2}(\xi)+\pi^{2} I_{1}^{2}(\xi)\right]} \mathrm{e}^{-\xi v_{s} t / r_{0}} \mathrm{~d} \xi+\tau_{0} \frac{r_{0}}{r} \end{aligned}\right. (13) 2. 数值计算
用MATLAB计算工具可得到数值解, 计算参数如下:孔洞半径r0=6m, τ0=100kPa, G=76 MPa, ρs=1 900kg/m3。为方便讨论计算结果, 将位移、应力和时间均进行量纲一化处理:
w^{*}=w G /\left(\tau_{0} r_{0}\right), \quad \tau^{\star}=\tau / \tau_{0}, \quad t^{\star}=t v_{\mathrm{s}} / r_{0} (14) 图 3为r=10, 20, 30m处土体的应力时程曲线。在反平面阶跃荷载作用下, 波的起跳时间为波由波源传播至该点所需要的时间, 当波传播到该点, 此处土体的应力和位移瞬间增大并达到最大值, 应力波离开后, 该处应力逐渐减小并逐渐趋于稳定值, 该稳定值与静力计算结果相吻合。3种不同半径处应力波起跳时间间隔为弹性波在此段距离传播需要的时间。由于应力波的发散传播, 距离波源越远, 应力值越小, 这符合弹性波的性质。
图 4为r=10, 20, 30m处土体位移时程曲线。在波到达之前, 该点的位移为零, 当波到达时, 此处位移瞬间增大到最大值, 随后逐渐减小并趋向于静力响应状态下的位移而保持不变。在r=10, 20, 30 m处最大量纲一位移分别为0.125 04、0.081 80和0.064 90, 相对应的量纲一时间为1.63、3.23和4.90, 由此同样可以得出与图 3相同的结论:3种不同半径处位移达到最大值的时间间隔为弹性波在此段距离传播需要的时间。结合图 3可知, 应力和位移的变化是同步的, 这也符合弹性波动理论中弹性波的传播性质。
由图 3~4还可以看出, 土体应力和位移最后的稳定值分别为被积函数D(ζ)和E(ζ)沿L3的积分值, 早期解的贡献主要是沿分支割线的积分, 这与文献[1]中关于压缩波入射的结论一致。
图 5和图 6分别为土体位移和应力的最大值以及静力值随半径的变化规律。由图 5~6可以看出, 土体所受动应力和动位移的最大值随距离波源距离的增大呈现衰减趋势, 这是由于弹性波的发散传播的特性, 其趋势与静力下的衰减趋势相近, 且相同情况下动力响应的衰减更慢, 随着传播距离的增大, 动力值与静力值之比越来越大, 因此在实际工程中动荷载的破坏性要大得多。
3. 计算结果验证
为了验证本文中计算结果的正确性, 用本文中的计算方法和F.Durbin[28]提出的拉普拉斯数值逆变换分别计算r=10m处的土体的应力和位移, 并将2种方法得出的结果做了比较, ,如图 7~8所示, 可以看出两者吻合较好。
4. 结论
利用Laplace变换和围道积分, 讨论了土体内圆柱形孔洞的瞬态响应问题, 求得了问题的解析表达式。可以得出以下结论:(1)通过将本文的计算结果与用F.Durbin[28]提出的拉普拉斯数值逆变换的计算结果和静力结果相比较, 验证了本文方法在研究洞室在反平面冲击荷载作用下的瞬态响应时的适用性和正确性。(2)土体应力和位移最后的稳定值由被积函数沿原点附近小圆的积分值贡献, 早期解的贡献主要是沿分支割线的积分, 即初始时刻, 分支割线上各点的贡献最大。(3)在波到达之前, 该处土体应力和位移都保持为零, 波到达之后, 应力和位移瞬间增大到最大值, 接着慢慢减小并逐渐趋于稳定值, 不同半径处应力和位移到达峰值的间隔即为弹性波在此段距离传播需要的时间。由于波沿径向发散传播, 距离波源越远, 应力和位移值越小, 相同的半径处应力和位移值相同。孔洞的该稳定值与静力下的受力相接近, 且应力和位移的变化是同步的。(4)在反平面动荷载作用下, 土体动应力和动位移的最大值随距离波源距离的增大呈现衰减趋势, 其趋势与静力值的衰减相近, 且相同情况下动力响应的衰减更慢, 因此在实际工程中危害性更大。
-
[1] Pao Yih-hsing, Mow C C. Diffraction of elastic waves and dynamic stress concentrations[M]. New York, USA: Adam Hilger Limited, 1973. [2] Lee J, Mal A K. A volume integral equation technique for multiple scattering problems in elastodynamics[J]. Applied Mathematics and Computation, 1995, 67(1/2/3): 135-159. https://www.sciencedirect.com/science/article/pii/009630039400057B [3] Davis C A, Lee V W, Bardet J P. Transverse response of underground cavities and pipes to incident SV waves[J]. Earthquake Engineering and Structural Dynamics, 2001, 30(3): 395-410. doi: 10.1002/eqe.14 [4] Iakovlev S. Interaction of a spherical shock wave and a submerged fluid-filled circular cylindrical shell[J]. Journal of Sound and Vibration, 2002, 255(4): 615-633. doi: 10.1006/jsvi.2001.4181 [5] Manolis G D. Elastic wave scattering around cavities in inhomogeneous continua by the BEM[J]. Journal of Sound and Vibration, 2003, 266(2): 281-305. https://www.sciencedirect.com/science/article/pii/S0022460X03001755 [6] Eason G. Propagation of waves from spherical and cylindrical cavities[J]. The Journal of Applied Mathematics and Physics, 1963, 14(1): 12-23. doi: 10.1007/BF01601142 [7] Eason G. The propagation of waves from a cylindrical cavity[J]. Journal of Composite Materials, 1973, 7(1): 90-99. doi: 10.1177/002199837300700107 [8] 张庆元, 战人瑞.爆轰载荷作用下球形空腔的动力响应[J].爆炸与冲击, 1994, 14(2): 182-185. http://www.bzycj.cn/article/id/10625Zhang Qing-yuan, Zhan Ren-rui. Dynamic response of a spherical cavity subjected to blast loads[J]. Explosion and Shock Waves, 1994, 14(2): 182-185. http://www.bzycj.cn/article/id/10625 [9] 刘国利, 赵会滨, 许贻燕.阶跃SH波作用下半圆形凹陷地形的瞬态反应:长期解[J].地震工程与工程振动, 1995, 15(1): 92-99.Liu Guo-li, Zhao Hui-bin, Xu Yi-yan. Transient response of semi-circular canyon under step SH wave: Long term solution[J]. Earthquake Engineering and Engineering Vibration, 1995, 15(1): 92-99. [10] Herman H, Klosner J M. Transient response of a periodically supported cylindrical shell Immersed in a fluid medium[J]. Journal of Applied Mechanics, 1965, 32(3): 562-568. doi: 10.1115/1.3627259 [11] Geers T L. Excitation of an elastic cylindrical shell by a transient acoustic wave[J]. Journal of Applied Mechanics, 1969, 36(3): 459-469. doi: 10.1115/1.3564702 [12] 杨峻, 宫全美, 吴世明, 等.饱和土体中圆柱形孔洞的动力分析[J].上海力学, 1996, 17(1): 37-45.Yang Jun, Gong Qun-mei, Wu Shi-ming, et al. Dynamic analysis of cylindrical holes in saturated soil[J]. Shanghai Mechanics, 1996, 17(1): 37-45. [13] Forrestal M J, Sagartz M J. Radiated pressure in an acoustic medium produced by pulsed cylindrical and spherical shells[J]. Journal of Applied Mechanics, 1971, 38(4): 1057-1060. doi: 10.1115/1.3408916 [14] Moodie T B, Barclay D W. Wave propagation from a cylindrical cavity[J]. Acta Mechanica, 1977, 27(1/2/3/4): 103-120. [15] Moodie T B, Haddow J B, Mioduchowski A, et al. Plane elastic waves henerated by dynamical loading applied to edge of circular hole[J]. Journal of Applied Mechanics, 1981, 48(3): 577-581. doi: 10.1115/1.3157677 [16] Akkas N, Erdogogan F. The residual variable method applied to the diffusion equation in cylindrical coordinates[J]. Acta Mechanic, 1989, 79(3/4): 207-219. doi: 10.1007/BF01187263 [17] Zakout U, Akkas N. Transient response of a cylindrical cavity with and without a bonded shell in an infinite elastic medium[J]. International Journal of Engineering Science, 1997, 35(12/13): 1203-1220. https://www.sciencedirect.com/science/article/pii/S0020722597000116 [18] Feldgun V R, Kochetkov A V, Karinski Y S, et al. Internal blast loading in a buried lined tunnel[J]. International Journal of Impact Engineering, 2008, 35(3): 172-183. doi: 10.1016/j.ijimpeng.2007.01.001 [19] 高盟, 高广运, 王滢, 等.内部荷载作用下圆柱形孔洞的动力响应解答[J].力学季刊, 2009, 30(2): 266-272.Gao Meng, Gao Guang-yun, Wang Ying, et al. Solution on dynamic response of a cylindrical cavity under internal load[J]. Chinese Quarterly of Mechanics, 2009, 30(2): 266-272. [20] 高盟, 高广运, 王滢, 等.饱和土与衬砌动力相互作用的圆柱形孔洞内源问题解答[J].固体力学学报, 2009, 30(5): 481-488.Gao Meng, Gao Guang-yun, Wang Ying, et al. Dynamic solutions of cylindrical cavities with the lining under internal load in the saturated soil[J]. Chinese Journal of Solid Mechanics, 2009, 30(5): 481-487. [21] 蔡袁强, 陈成振, 孙宏磊.黏弹性饱和土中隧道在爆炸荷载作用下的动力响应[J].浙江大学学报:工学版, 2011, 45(9): 1657-1663. doi: 10.3785/j.issn.1008-973X.2011.09.024Cai Yuan-qiang, Chen Cheng-zhen, Sun Hong-lei. Dynamic response of tunnel in viscoelastic saturated soil subjec-ted to blast loads[J]. Journal of Zhejiang University: Engineering Science, 2011, 45(9): 1657-1663. doi: 10.3785/j.issn.1008-973X.2011.09.024 [22] Haddow J B, Lorimer S A, Tait R J. Nonlinear axial shear wave propagation in a hyperelastic incompressible solid[J]. Acta Mechanica, 1987, 66(1/2/3/4): 205-216. doi: 10.1007/BF01184294 [23] Haddow J B, Jiang L. Finite amplitude azimuthal shear waves in a compressible hyperelastic solid[J]. Journal of Applied Mechanics, 2001, 68(2): 145-152. doi: 10.1115/1.1334862 [24] Watanabe K, Payton R G. SH wave in a cylindrically anisotropic elastic solid a general solution for a point source[J]. Wave Motion, 1996, 25(2): 197-212. https://www.sciencedirect.com/science/article/pii/S0165212596000418 [25] Barclay D W. Wavefront expansion for non-linear axial shear wave propagation[J]. International Journal of Nonlinear Mechanics, 1998, 33(2): 259-274. doi: 10.1016/S0020-7462(97)00016-4 [26] Barclay D W. Shock front analysis for axial shear wave propagation in a hyperelastic incompressible solid[J]. Acta Mechanica, 1999, 133(1/2/3/4): 105-129. doi: 10.1007%2FBF01179013 [27] Barclay D W. Shock calculations for axially symmetric shear wave propagation in a hyperelastic incompressible solid[J]. International Journal of Non-linear Mechanics, 2004, 39(1): 101-121. doi: 10.1016/S0020-7462(02)00141-5 [28] Durbin F. Numerical inversion of Laplace transformation: An efficient improvement to Durbin and Abatep's method[J]. The Computer Journal, 1974, 17(4): 371-376. doi: 10.1093/comjnl/17.4.371 [29] 梁昆淼.数学物理方法[M].北京: 高等教育出版社, 2010. [30] Watson G N. Theory of Bessel function[M]. Cambridge, UK: Cambridge University Press, 1995. -








 下载:
下载:









 下载:
下载: