A compressible model of radial crater growth by shaped-charge jet penetration
-
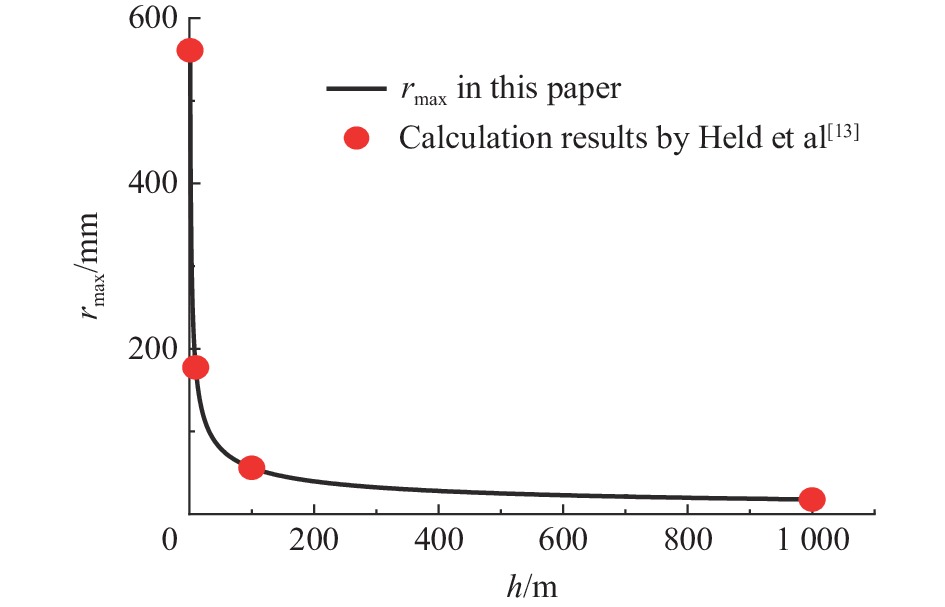
摘要: 聚能射流侵彻厚靶时，对靶材同时进行轴向和径向挤压进而发生轴向侵彻和径向扩孔。本文中基于聚能射流侵彻可压缩模型并结合Szendrei-Held扩孔方程，推导给出考虑弹/靶材料可压缩性的聚能射流扩孔方程。为简化完整可压缩模型繁琐的计算过程，又基于Murnaghan状态方程给出可压缩模型的近似解。与水中聚能射流扩孔的实验研究对比分析，表明该模型预测优于Szendrei-Held扩孔方程。模型分析表明，射流半径、驻点压力、靶材强度、驻点处靶材密度以及聚能射流速度是影响聚能射流扩孔的主要因素。本文模型可以更准确地预测聚能射流侵彻可压缩性较强的靶材的扩孔情况。相关工作可为含液密闭结构干扰聚能射流侵彻提供理论基础。Abstract: A shaped-charge jet compresses the target axially and radially simultaneously when the jet penetrates into a thick target, and then the axial penetration and radial crater growth occur. The research on axial penetration is abundant, but the research on radial crater growth is less and there is a certain error between theoretical prediction and experimental results. The radial crater growth equation of the shaped-charge jet was derived by considering the compressibility of the jet and target materials based on the compressible model of shaped-charge jet penetration and the Szendrei-Held equation. The main changes of equations are the stagnation pressure adopted value of the compressible model and the density changed with jet velocity. An approximate solution of the compressible model was given based on the Murnaghan equation of state in order to simplify the tedious calculation process of the complete compressible model, i.e., the calculation processes of stagnation pressure and density change were simplified. The prediction by this model is better than that by the Szendrei-Held equation compared with the experimental study of the shaped-charge jet crater growth in water. The main factors affecting the radial crater growth by the shaped-charge jet include jet radius, stagnation point pressure, target strength, target density at the stagnation point and shaped-charge jet velocity. This model can more accurately predict the crater growth of the shaped-charge jets penetrating into the compressible targets. It may be helpful to study the interference of shaped-charge jet penetration with liquid-confined structures.
-
Key words:
- shaped-charge jet /
- radial crater growth /
- compressible model /
- thick target
-
图 1 侵彻速度与扩孔速度分布及侵彻过程中的流场
Figure 1. Distribution of penetration velocity and radial crater velocity, flow field during penetration
图 2 不同方法获得的扩孔孔径随时间变化的比较
Figure 2. Comparison of crater radius varying with time among different methods
图 3 靶材最大扩孔半径与水深度的关系
Figure 3. Relationship between the maximum target crater radius and the water depth
图 4 靶材最大扩孔半径与射流半径的关系（h=10 m）
Figure 4. Relationship between the maximum target crater radius and the jet radius (h=10 m)
图 5 水、铝和铜的Hugoniot压力曲线
Figure 5. Hugoniot pressure curves for water, aluminium and copper
图 6 射流侵彻靶材的驻点压力随射流速度的变化
Figure 6. Stagnation point pressure of jets penetrating targets varying with jet velocity
表 1 材料的Mie-Grüneisen状态方程和Murnaghan状态方程参数
Table 1. Material parameters of Mie-Grüneisen and Murnaghan equations of state
下载: 导出CSV
-
[1] SONG W J, CHEN X W, CHEN P. Effect of compressibility on the hypervelocity penetration [J]. Acta Mechanica Sinica, 2018, 34(1): 82–98. DOI: 10.1007/s10409-017-0688-1. [2] BIRKHOFF G, MACDOUGALL D P, PUGH E M, et al. Explosives with lined cavities [J]. Journal of Applied Physics, 1948, 19(6): 563–582. DOI: 10.1063/1.1698173. [3] EICHELBERGER R J. Experimental test of the theory of penetration by metallic jets [J]. Journal of Applied Physics, 1956, 27(1): 63–68. DOI: 10.1063/1.1722198. [4] ALLISON F E, VITALI R. A new method of computing penetration variables for shaped-charge jets: BRL Report No. 1184 [R]. Aberdeen Proving Ground, USA: Ballistic Research Laboratories, 1963. [5] HAUGSTAD B S. Compressibility effects in shaped charge jet penetration [J]. Journal of Applied Physics, 1981, 52(3): 1243–1246. DOI: 10.1063/1.329745. [6] HAUGSTAD B S, DULLUM O S. Finite compressibility in shaped charge jet and long rod penetration: the effect of shocks [J]. Journal of Applied Physics, 1981, 52(8): 5066–5071. DOI: 10.1063/1.329450. [7] FLIS W J, CHOU P C. Penetration of compressible materials by shaped-charge jets [C]//Proceedings of the 7th International Symposium on Ballistics. Hague, Netherlands: International Ballistics Society, 1983: 617–625. [8] FLIS W J. A model of compressible jet penetration [C]//Proceedings of the 26th International Symposium on Ballistics. Miami, Florida, USA: International Ballistics Society, 2011: 1124–1132. [9] SONG W J, CHEN X W, CHEN P. A simplified approximate model of compressible hypervelocity penetration [J]. Acta Mechanica Sinica, 2018, 35(5): 910–924. DOI: 10.1007/s10409-018-0769-9. [10] SZENDREI T. Analytical model for crater formation by jet impact and its application on penetration curves and profiles [C]//Proceedings of the 7th International Symposium on Ballistics. Hague, Netherlands: International Ballistics Society, 1983: 575–583. [11] HELD M, JIANG D C M, CHANG C C, et al. Crater-growing process in water by shaped-charge perforation [C]//Proceedings of the SPIE 2513, 21st International Congress on High-Speed Photography and Photonics. Taejon, Korea: International Society for Optical Engineering, 1995: 1017–1027. DOI: 10.1117/12.209562. [12] HELD M. Verification of the equation for radial crater growth by shaped charge jet penetration [J]. International Journal of Impact Engineering, 1995, 17(1/2/3): 387–398. DOI: 10.1016/0734-743X(95)99864-N. [13] HELD M, HUANG N S, JIANG D, et al. Determination of the crater radius as a function of time of a shaped charge jet that penetrates water [J]. Propellants, Explosives, Pyrotechnics, 1996, 21(2): 64–69. DOI: 10.1002/prep.19960210203. [14] 肖强强, 黄正祥, 顾晓辉. 冲击波影响下的聚能射流侵彻扩孔方程 [J]. 高压物理学报, 2011, 25(4): 333–338. DOI: 10.11858/gywlxb.2011.04.008.XIAO Q Q, HUANG Z X, GU X H. Equation of penetration and crater growth by shaped charge jet under the influence of shock wave [J]. Chinese Journal of High Pressure Physics, 2011, 25(4): 333–338. DOI: 10.11858/gywlxb.2011.04.008. [15] GUO M, ZU X D, SHEN X J, et al. Study on liquid-filled structure target with shaped charge vertical penetration [J]. Defence Technology, 2019, 15(6): 861–867. DOI: 10.1016/j.dt.2019.05.003. [16] ZU X D, HUANG Z X, GUAN Z W, et al. Influence of a liquid-filled compartment structure on the incoming shaped charge jet stability [J]. Defence Technology, 2021, 17(2): 571–582. DOI: 10.1016/j.dt.2020.03.009. [17] LI G, CHEN X W, SONG W J. Compressible models of shaped charge jet in water [J]. Mechanics of Solids, in press, 2022. DOI: 10.3103/S0025654422040112. [18] MEYERS M A. Dynamic behavior of materials [M]. New York, USA: Wiley, 1994. [19] FLIS W J. A simplified approximate model of compressible jet penetration [C]//Proceedings of the 27th International Symposium on Ballistics. Freiburg, Germany: International Ballistics Society, 2013: 1252–1263. [20] HELD M, KOZHUSHKO A A. Radial crater growing process in different materials with shaped charge jets [J]. Propellants, Explosives, Pyrotechnics, 1999, 24(6): 339–342. DOI: 10.1002/(SICI)1521-4087(199912)24:6<339::AID-PREP339>3.0.CO;2-5. -
计量
- 文章访问数: 684
- HTML全文浏览量: 308
- PDF下载量: 112
- 被引次数: 0