Analysis on dynamic compressive behavior of concrete based on a 3D mesoscale model
-
摘要: 通过建立混凝土的3D细观模型,在细观尺度上分析动态压缩荷载作用下混凝土材料内部裂缝的产生和发展、损伤演化和动态强度及其影响因素。首先,基于传统的“生成-投放”法生成粒径、形状和空间分布均随机的凸多面体粗骨料模型,并通过骨料沉降和粒径缩放实现粗骨料的大体积率(达50%)和可调控;使用四面体网格划分骨料和砂浆表征其真实物理形状;使用界面粘结接触表征界面过渡区(ITZ)提升计算效率。进一步通过对比不同粗骨料粒径混凝土的分离式霍普金森压杆(SHPB)试验数据与模拟结果,如杆上应变时程、试件动态应力-应变曲线和试件损伤破坏模式,验证了建立的混凝土3D细观有限元模型、参数确定方法和数值仿真方法的准确性。最后,分析了30~100 s−1应变率范围内骨料粒径(4~8、10~14和22~26 mm)、体积率(20%、30%和40%)和类型(石灰岩、花岗岩和玄武岩)对混凝土动态压缩强度的影响。结果表明:粗骨料粒径增大,混凝土动态压缩强度先增大后减小;粗骨料体积率越高,混凝土动态压缩强度越大;混凝土动态压缩强度随粗骨料强度的增加而提高。Abstract: As the most widely used construction material, concrete is common in military protection and civil transportation infrastructures. During its services life, concrete may bear dynamic loads such as high-speed penetration, blast and impact of vehicle, ship, rockfall and so on. On the mesoscale, concrete is three-phase material composed of mortar, coarse aggregates and interface transition zone (ITZ). The concrete 3D mesoscale model was established to analyze the crack generation and development, damage evolution, dynamic strength and its influencing factors of concrete. Firstly, randomly distributed convex polyhedron aggregates of random shapes and sizes were modeled based on the conventional “take-and-place” method and Monte Carlo algorithm, and drop of aggregates under gravity were simulated in finite element software LS-DYNA to make aggregates more dense, improving aggregate volume fraction to 50%. After that, aggregate size was reduced by a trial value to control aggregate volume fraction conveniently. Then, aggregates and mortar were meshed with tetrahedral elements to display their actual physical shapes. Besides, ITZ was represented by interface cohesive contact which equals zero-thickness bonding elements to improve computational efficiency. Furthermore, SHPB simulations of different coarse aggregates sizes concrete were conducted and the accuracy of finite element model, parameter determination method and numerical simulation methods were proved by comparing test and simulated bar strain-time history, dynamic stress-strain curves and failure patterns of specimens. Finally, influences of the aggregate size (4−8, 10−14 and 22−26 mm), volume fraction (20%, 30% and 40%) and type (limestone, granite and basalt) on concrete dynamic compressive strength under the strain rate within 30−100 s−1 were analyzed. It shows that the dynamic compressive strength of concrete increases first and then decreases with the increase of aggregate size; the dynamic compressive strength of concrete increases with the increase of volume fraction; the dynamic compressive strength of concrete increases with the increase of aggregate strength.
-
Key words:
- concrete /
- 3D mesoscale model /
- dynamic mechanical behavior /
- cohesive contact /
- strain rate effect
-
混凝土作为最常用的建筑材料,广泛应用于军事防护工程和民用交通基础设施中,其在服役期内可能承受弹体和破片的高速侵彻、爆炸以及车、船和落石冲击等动态荷载作用。因此,混凝土的动态力学行为一直是防护工程领域重点关注的研究方向之一。
大量试验表明,混凝土的动态强度高于其准静态强度[1-7],即呈现明显的应变率效应。分离式霍普金森压杆(split Hopkinson pressure bar, SHPB)装置是研究混凝土材料动态力学行为的常用试验装置[8],通常试验应变率范围为10~103 s−1。Hao等[9]对最大骨料粒径分别为4和8 mm的混凝土试件开展了SHPB试验,结果表明混凝土动态压缩强度随着骨料粒径的减小和体积率的增大而增大。而王江波等[10]对不同骨料粒径混凝土开展了SHPB试验,发现混凝土动态压缩强度随着骨料粒径的增大呈现先增大后减小的趋势。上述工作表明粗骨料对混凝土的动态压缩性能影响较大,然而采取试验手段分析粗骨料影响实施较为复杂且结果存在一定离散性,较难得出规律性结论。
混凝土在细观尺度上由砂浆、粗骨料和界面过渡区(interface transition zone, ITZ)三相成分组成。从细观尺度研究混凝土的动态力学性能可以直观地展示混凝土内部骨料和砂浆的损伤破坏情况。因此,部分学者通过建立混凝土细观模型研究其动态力学行为。郭瑞奇等[11]建立了包括球形粗骨料和砂浆的混凝土3D二相细观模型,即忽略ITZ并假定砂浆和骨料间为理想粘结,进一步基于上述模型分析了骨料体积率和粒径对混凝土动态压缩强度和应力均匀性的影响。结果表明骨料体积率越高,粒径越小,混凝土试件整体的应力均匀性越好且动态强度越高。Zhou等[12]使用2D轴对称三相细观模型研究了混凝土在应变率10~104 s−1范围内的动态压缩行为,其中混凝土细观模型包括砂浆、圆形骨料和50 μm厚度的ITZ,采用映射法划分网格,网格尺寸为50 μm。结果表明在高应变率下试件出现更多裂缝且剪切破坏更为明显。Pająk等[13]通过建立包括砂浆、球形骨料和ITZ的3D细观模型,对68~236 s−1应变率范围内混凝土的动态力学性能进行了数值仿真分析,发现应变率低于200 s−1时惯性效应对动态增强因子(dynamic increase factor, DIF, 记为F,为动态强度与准静态强度之比)的贡献不足10%。Lv等[14]和Wu等[15]基于包括多面体骨料、砂浆和ITZ,并采用映射法划分网格的3D三相细观模型研究了混凝土的动态力学性能,其中Lv等[14]将10~150 s−1应变率范围内混凝土的破坏模式分为剥落、破裂、碎裂和粉碎四种,Wu等[15]得出混凝土强度越大,DIF越小。Zhou等[16]建立了包括多面体骨料、砂浆和ITZ,并采用四面体网格划分的3D三相细观模型,考察了骨料在混凝土动态损伤破坏中的作用,发现在试件应变率高于50 s−1时,骨料自身发生断裂。
然而,上述基于细观模型的混凝土动态力学性能研究还存在以下不足:(1) 细观建模方面,郭瑞奇等[11]、Zhou等[12]和Pająk等[13]使用圆形或球形模拟粗骨料,与实际形状不符;真实ITZ厚度为20~50 μm,Pająk等[13]、Lv等[14]和Wu等[15]为便于建模,将其厚度简化为0.5~2 mm,与真实情况不符;尽管Zhou等[12]使用50 μm网格,尽可能还原ITZ厚度,然而上述网格尺寸严重影响了计算效率;Lv等[14]和Wu等[15]使用映射法划分网格,对骨料边缘进行锯齿状处理,这也与真实骨料物理形状相悖;基于传统的“生成-投放”法得到的多面体骨料体积率一般低于30%[17-18],远低于真实混凝土40%~50%的粗骨料体积率;(2) 3D细观模型方面,对不同加载速率尤其是较高应变率(10~102 s−1)下不同骨料粒径混凝土动态压缩行为的验证工作还比较缺乏,从而对于粗骨料粒径、体积率和类型对混凝土动态压缩行为的影响还没有定量的结论。
本文基于混凝土3D细观模型对混凝土的动态压缩力学行为以及粗骨料参数的影响开展数值模拟。首先,基于传统的“生成-投放”法在给定空间区域内随机投放随机多面体骨料;对骨料进行重力沉降实现其密实分布,进一步进行骨料缩放得到目标骨料体积率;使用显式有限元分析程序LS-DYNA建立包含随机多面体粗骨料、砂浆和ITZ的混凝土3D有限元模型,其中砂浆和骨料使用四面体网格划分并采用Riedel-Hiermaier-Thoma (RHT)[19-20]材料模型描述其动态力学性能和损伤演化,ITZ采用粘结接触表征,并确定模型参数取值。进一步基于建立的混凝土3D细观有限元模型,对王江波等[10]开展的纯砂浆以及不同粒径粗骨料(4~8、10~14和22~26 mm)混凝土的SHPB试验进行数值仿真,通过对比反射波和透射波引起的入射杆和透射杆上的应变时程,以及试件材料的动态应力-应变曲线和破坏模式,对建立的混凝土3D细观有限元模型、参数取值和数值仿真方法的可靠性进行评估。最后,开展混凝土骨料粒径、体积率和类型对其动态压缩强度的参数影响分析,并与已有相关试验结论进行对比验证。
1. 随机骨料建模方法
本节基于传统“生成-投放”参数化建模方法,在球体内接多面体生成随机多面体粗骨料,并使用蒙特卡洛算法将骨料投放到预定空间中的随机位置。通过外接球判断准则确保骨料不超出边界且互相不侵入。进一步对随机分布骨料模型进行重力沉降和粒径缩放,得到目标骨料体积率。
1.1 随机凸多面体骨料生成
使用随机多面体表征混凝土碎石粗骨料的不规则形状。首先根据Fuller级配公式确定各粒径范围内的骨料百分比,即粒径小于da的骨料质量占比为
(da/da,max)0.5 ,其中da,max为最大骨料直径。然后按照粒径从大到小的顺序生成骨料。基于MATLAB软件,在骨料的粒径范围内,通过蒙特卡洛算法随机确定骨料粒径2R0,得到直径为2R0的球体。进一步使用延拓法在该球体内接多面体生成随机骨料,如图1(a)所示。首先以坐标系原点为圆心,在xOy平面内生成半径为R0的基圆,在基圆上随机确定4个顶点A(−R0, 0, 0)、B(xB, yB, 0)、C(R0, 0, 0)和D(xD, yD, 0)连成随机四边形。为避免出现尖角状畸形四边形,通过以下条件约束B和D点的坐标:{x2B+y2B=R200.7R0<xB≤R0−R0<yB<R0,{x2D+y2D=R20−R0≤xD<−0.7R0−R0<yD<R0 (1) 在以原点为球心、半径为R0的球体上,沿着z轴正负方向分别随机生成E点(xE,yE,zE)和F点(xF,yF,zF),连接E和F点与A、B、C和D点,生成随机八面体。为防止尖角状和片状畸形八面体的出现,E和F点坐标需满足:
{x2E+y2E+z2E=R20−0.2R0<xE<0.2R0−0.2R0<yE<0.2R00<zE≤R0{x2F+y2F+z2F=R20−0.2R0<xF<0.2R0−0.2R0<yF<0.2R0−R0≤zF<0 (2) 检索该八面体的所有边,找出其中的最长边,假设为AE边,在AE边上随机取一点P,其坐标为:
→OP=→OA+α→AE (3) 为避免生成畸形多面体,限制
0.3≤α≤0.7 。假设与AE边相邻的两个面的单位外法向量分别为v1和v2,v1+v2=v,沿着v方向向外延伸P点与球相交于G点。删除最长边AE及其两个相邻面,连接G点与A、B、D和E点,得到随机凸十面体。循环上述操作N次,可生成面数为10+2N的随机凸多面体。需要指出的是,本文不讨论骨料面数的影响,粗骨料均为二十四面体。进一步以原点为基点,将上述生成的多面体分别绕x、y和z轴旋转0~2π范围内的随机角度
γx 、γy 和γz 以增加随机骨料空间分布的多样性。至此,在原点处生成了粒径和形状随机的多面体骨料。1.2 骨料随机投放
生成一个粒径和形状随机的多面体骨料后,需要将其随机投放到指定区域内以实现骨料的空间随机分布。以边长分别为Lx、Ly和Lz的棱柱体空间为例,通过蒙特卡洛算法随机生成一组坐标作为骨料投放后的中心点位置,基于外接球法判断骨料投放至该位置后是否在边界以内,并且不侵入其他骨料,判断条件分别为:
{Ri<Xi<Lx−RiRi<Yi<Ly−RiRi<Zi<Lz−Ri (4) √(Xi−n−Xi)2+(Yi−n−Yi)2+(Zi−n−Zi)2>Ri−n+Ri (5) 式中:i为目前正在投放的骨料编号;(Xi−n,Yi−n,Zi−n)为先前投放的第i−n个骨料的外接球球心坐标,且1≤n≤i−1;Ri和Ri−n分别为第i和i−n个骨料外接球的半径。如果该骨料位置满足以上两个条件,则接受该骨料位置,若不满足,则重新生成骨料,并重复以上步骤。
1.3 骨料沉降与缩放
上述“生成-投放”算法生成的随机多面体粗骨料模型的骨料体积率最高可达25%,为提高粗骨料体积率,目前主要有几何法和动力法两种方法。其中几何法基于纯几何运算,通过计算骨料间的距离、移动骨料缩小骨料间距,从而实现骨料密实,该方法对圆形和球体骨料适用度较高,而对于距离计算较为复杂的多面体骨料适用性较差;动力法基于动力计算,引入骨料重力和碰撞接触力的作用,但自编动力计算算法难度较高。本文基于LS-DYNA,提出一种结合骨料重力沉降和粒径缩放的方法,实现骨料体积率在0~50%范围内可调控。
首先在高度为目标投放区域高度三倍的区域内随机投放骨料,体积率约为20%,然后将上述模型导入有限元前处理软件Hypermesh,为骨料赋予刚体材料模型。对骨料施加重力使其向下方密实沉降,从而获得完全密实的骨料模型。同时为避免骨料沉降过程中超出指定区域,在骨料外建立实体围挡,如图1(b)所示。为围挡赋予弹性材料,骨料和围挡的密度和弹性模量均分别取8000 kg/m3和200 GPa。骨料之间以及骨料与围挡之间通过关键字*CONTACT_AUTOMATIC_SURFACE_TO_SURFACE定义接触,摩擦因数取0.1。
图1(b)给出了沉降前后的骨料模型,密实沉降后骨料模型的体积率约为50%。为得到与目标体积率一致的骨料模型,进一步对骨料进行粒径缩放处理,如图2(a)所示。即将各骨料所有顶点沿着顶点与中心点连线方向内移一定值q,q由目标体积率确定。骨料中心点Q坐标为各顶点坐标之和的平均值,即:
(xQ,yQ,zQ)=1mm∑j=1(xj,yj,zj) (6) 式中:m为骨料节点数量,(xj,yj,zj)为第j个节点的坐标。节点P经过骨料粒径缩放得到新的节点
P′ 与中心点Q的连线向量为:→OP′=→QP(1−q/|→QP|) (7) O为坐标原点,
P′ 点坐标为:(xP′,yP′,zP′)=→OQ+→QP′=→OP−q→QP|→QP|=(xj,yj,zj)−q⋅(xj−xQ,yj−yQ,zj−zQ)√(xj−xQ)2+(yj−yQ)2+(zj−zQ)2 (8) 该方法可得到0~50%之间任意体积率的随机骨料分布模型,如图2(b)~(e)所示,实现了骨料体积率的可调控。
2. 混凝土3D细观有限元模型
在上述生成的随机分布粗骨料模型基础上,根据骨料节点信息生成骨料几何模型,通过布尔运算生成砂浆几何模型,并使用四面体网格划分砂浆和骨料。进一步使用Riedel-Hiermaier-Thoma (RHT) 材料模型描述砂浆和骨料的力学行为,采用等效于零厚度粘结单元的粘结接触表征ITZ,建立混凝土的3D细观有限元模型。
2.1 3D细观有限元模型
在随机分布骨料模型的基础上,首先导出骨料的节点坐标信息和面信息,编写ANSYS APDL命令流文件生成骨料的几何模型。将骨料几何模型导入前处理软件Hypermesh,通过布尔运算减除的操作分离出砂浆的几何模型,如图3(a)所示。进一步对骨料进行网格划分,如图3(b)所示,由于六面体网格对骨料和砂浆边缘进行锯齿状近似处理,而四面体可以准确地表征骨料的物理形状,因此本文采用四面体网格划分砂浆和骨料,如图3(c)所示。ITZ采用等效于零厚度粘结单元的粘结接触表征。
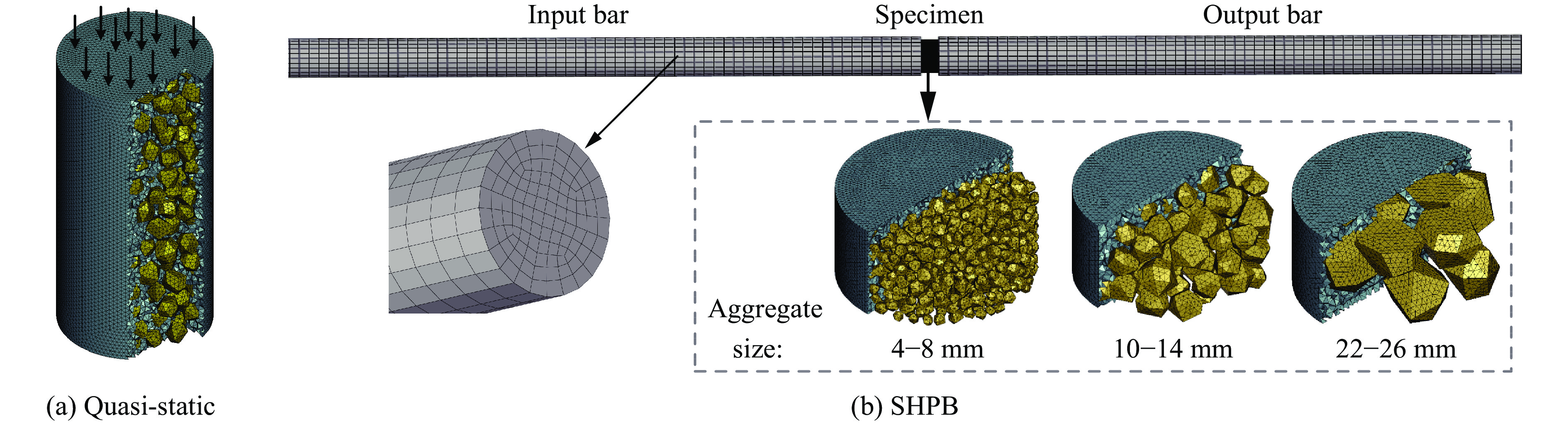
已有混凝土材料的SHPB试验大多未明确给出粗骨料粒径范围,因此选取王江波等[10]开展的纯砂浆基体和粗骨料粒径范围分别为4~8、10~14和22~26 mm的混凝土准静态压缩和SHPB动态压缩试验,分别记为M、G6、G12和G24。图4给出了准静态试验和动态SHPB试验的3D细观模型,其中SHPB装置由入射杆、透射杆和试件组成,入射杆和透射杆的直径均为80 mm,长度分别为6000和4000 mm,沿径向和轴向网格尺寸分别取6和20 mm。通过将混凝土试件网格尺寸分别取为1~4 mm进行网格敏感性分析,得到的反射和透射波如图5所示。可以看出网格尺寸为1~3 mm时应力波形基本重合,综合考虑损伤模拟效果和计算效率,取试件网格尺寸为2 mm。
2.2 砂浆和骨料材料模型及参数
本文采用了适用于描述混凝土类材料在强动载作用下的动态响应和损伤破坏的RHT材料模型[19-20]描述砂浆和骨料的动态力学行为。该模型在主应力空间引入了3个强度极限面,即:弹性屈服面、最大失效面和残余强度面,并使用静水压p、有效应力σeff和罗德角θ定义,如图6(a)所示。相应的材料偏应力-应变关系分为3个阶段,即弹性阶段(S1S2)、应变硬化阶段(S2S3)和软化阶段(S3S4),如图6(b)所示,其中
σe 、σf 和σr 分别为弹性屈服面、最大失效面和残余强度面强度。(1) 最大失效面描述材料可承受的最大应力,表达式为:
σf(p∗,θ,˙εp)=fcσ∗f[p∗,F(˙εp,p∗)]R3(θ,p∗) (9) 式中:fc为圆柱体单轴压缩强度;
p∗=p/fc 为归一化静水压力;˙εp 为塑性应变率;σ*f 表示θ=0即压缩的归一化失效应力;F为动态增强因子(DIF),用于描述应变率效应;R3为考虑应力三轴性的William-Warnke函数。σ*f 和F的表达式为:σ*f(p∗,F)={Af[p∗−F/3+(Af/F)−1/n]np*≥F/3Ff*s/Q1+3p∗(1−f*s/Q1)F/3>p∗≥0Ff*s/Q1−3p∗[1/Q2−f*s/(Q1f*t)]0>p∗>p*t0p*t>p∗ (10) F(˙εp)={(˙εp/˙ε0)β˙εp≤˙εc,tpγ(˙εp)1/3˙εp>˙εc,tp (11) 式中:Af为失效面参数;
f*s 为剪压强度比;f*t 为拉压强度比;p*t=FQ2f*sf*t/3(Q1f*t−Q2f*s) 为归一化失效截止压力,Q1和Q2分别控制剪切和拉伸子午线;β为应变率指数,表示压缩和拉伸时分别记为βc 和βt ;γ为应变率系数,表示拉伸和压缩时分别记为γc 和γt ;˙εc,tp 为压缩/拉伸过渡应变率。具体的:βc=15+(3/4)fc,βt=110+(1/2)fc,lgγc=6βc−0.492,lgγt=7βt−0.492 (12) (2) 弹性屈服面描述材料开始进入塑性时的强度,表达式为:
σe(p∗,θ,˙εp)=σf(p∗,θ,˙εp)Fe(p∗)Fh(p∗) (13) 式中:Fe为弹性系数,Fh为帽盖函数。
(3) 残余强度面描述材料残余强度,表达式为:
σr(p∗)={fcAr(p∗)nrp∗>00p∗≤0 (14) 式中:Ar和nr分别为残余强度参数和指数。
(4) RHT模型中的损伤为塑性应变的累积,损伤因子定义为
D=∑(Δεp/εfp) (15) 式中:
εfp 为最大塑性应变,表达式为εfp=max{D1(p∗−(1−D)p*t)D2,εmp} (16) 式中:D1和D2分别为损伤系数与损伤指数,
εmp 为最小失效应变。如图7所示,与王江波等[10]由60 MPa砂浆材料的SHPB试验获得的DIF对比发现,RHT材料模型默认压缩应变率指数βc=0.02高估了砂浆的应变率效应。根据试验数据对式(11)进行拟合,参考欧洲国际混凝土委员会规范[22],取过渡压缩应变率
˙εcp =30 s−1,得到压缩应变率指数βc=5.64×10−3。砂浆抗压强度为60 MPa,弹性模量为28 GPa,其他RHT模型参数见表1所示。骨料抗压强度取110 MPa,弹性模量为50 GPa,其他RHT参数取默认值。表 1 砂浆的RHT模型参数Table 1. RHT model parameters of mortar参数类型 参数 符号 取值 参数类型 参数 符号 取值 基本强度参数 拉压强度比 f*t 0.18 失效面参数 失效面参数 Af 1.6 剪压强度比 f∗s 0.1 失效面指数 N 0.61 弹性屈服面参数 压缩屈服面参数 g∗c 0.53 拉压子午比 Q0 0.6805 拉伸屈服面参数 g∗t 0.7 罗德角相关系数 BL 0.0105 残余强度面参数 残余强度参数 Ar 1.4 压缩应变率指数 βc 5.64×10−3 残余强度指数 nr 0.61 拉伸应变率指数 βt 0.02 硬化段参数 剪切模量缩减系数 ξ 0.9 参考压缩应变率 ˙εc0 3×10−5 s−1 软化段参数 损伤参数 D1 0.02 参考拉伸应变率 ˙εt0 3×10−6 s−1 损伤指数 D2 1 过渡压缩应变率 ˙εcp 30 s−1 最小失效应变 εmp 0.01 过渡拉伸应变率 ˙εtp 30 s−1 2.3 ITZ表征及参数
在LS-DYNA R11中,ITZ可通过接触表征,使用关键字*CONTACT_AUTOMATIC_ SURFACE_TO_SURFACE_TIEBREAK定义,OPTION选项为9时等效于使用138号材料模型的零厚度粘结单元[20]。如图8所示,该接触引入法向张开(Ⅰ型)、切向滑移(Ⅱ型)以及同时受法向和切向力的混合模式。使用双线性牵引-分离关系描述界面的拉伸和剪切性能,包括线性加载段和线性软化段。在未损伤的加载段刚度恒定,接触应力与界面滑移的关系为:
[σnσs]=[Kn00Ks][δnδs] (17) 式中:σn和σs分别为法向和切向应力,Kn和Ks分别为法向和切向刚度。当界面滑移超过初始损伤滑移后进入线性软化段,随着界面滑移增大,接触应力线性减小,并且在界面滑移超过完全破坏滑移时降为零,即粘结接触失效。失效后接触转变为普通的面面接触,可同时传递压力和摩擦力。
对于Ⅰ型和Ⅱ型,界面的初始损伤滑移
δ(0) 和完全破坏滑移δ(F) 分别为δ(0)Ⅰ=TKn,δ(0)Ⅱ=SKs,δ(F)Ⅰ=2GCⅠT,δ(F)Ⅱ=2GCⅡS (18) 式中:T和S分别为法向和切向强度,
GCⅠ 和GCⅡ 分别为法向和切向断裂能。对于混合模式,接触界面相对位移为δm=√δ2Ⅰ+δ2Ⅱ ,界面初始损伤和完全破坏的相对位移δ(0) 和δ(F) 表达式分别为δ(0)=δ(0)Ⅰδ(0)Ⅱ√1+β2(δ(0)Ⅱ)2+(βδ(0)Ⅰ)2,δ(F)=2(1+β2)1/γ[GCⅠ+(GCⅡ−GCⅠ)(β2KsKn+β2Ks)a]δ(0)(Kγn+β2Kγs)1/γ (19) 式中:
β=δⅠ/δⅡ ,可反映混合度;a=2为混合指数;γ =2为无量纲有效分离参数[20]。ITZ被视为多孔的砂浆,其特征参数取值通常劣化为砂浆的50%~90%[23-24]。在准静态情况下,ITZ的法向强度取砂浆拉伸强度的70%,对于王江波等[10]试验取4.2 MPa。在动态荷载情况下,由于该接触无法描述应变率效应,故通过试算确定合适的ITZ强度值。与准静态情况下相同,ITZ的动态法向强度也取砂浆动态拉伸强度的70%。欧洲国际混凝土委员会规范[22]给出混凝土的拉伸DIF为:
Ftr={(˙εt/˙εt0)0.018˙εt≤10 s−10.0062(˙εt/˙εt0)1/3˙εt>10 s−1 (20) 式中:
˙εt 为拉伸应变率,˙εt0 =1×10−6 s−1为参考拉伸应变率。基于式(20)可得拉伸应变率˙εt 在30~100 s−1范围时,砂浆的拉伸DIF范围为1.93~2.87,则ITZ的动态法向强度与准静态法向强度的比值也应在上述变化范围。基于文献[10]中粗骨料粒径为10~14 mm、应变率为40 s−1的工况试算发现:当ITZ的动态法向强度(9 MPa)为静态法向强度的2.14倍时,模拟结果与试验较为吻合。进一步参照Wang等[25]验证的一套ITZ参数(法向强度3.5 MPa,切向强度10.5 MPa,法向断裂能0.03 N/mm和切向断裂能0.09 N/mm)线性缩放获得本文一系列ITZ参数,即:法向强度T=9 MPa,切向强度S=27 MPa,法向断裂能GCⅠ =0.08 N/mm,切向断裂能GCⅡ =0.24 N/mm。后续的数值模拟中均采用上述ITZ参数。3. 混凝土SHPB试验模拟
王江波等[10]开展的SHPB试验中混凝土应变率范围为30~100 s−1。本文通过直接在入射杆端输入试验加载波形对试件施加动态压缩荷载;入射杆和透射杆均赋予弹性材料,密度为7850 kg/m3,弹性模量为210 GPa,泊松比为0.22;使用RHT材料模型表征砂浆和骨料的力学性能,材料参数见2.2节;为重现冲击荷载作用下试件的断裂,砂浆和骨料的失效应变均取0.2。
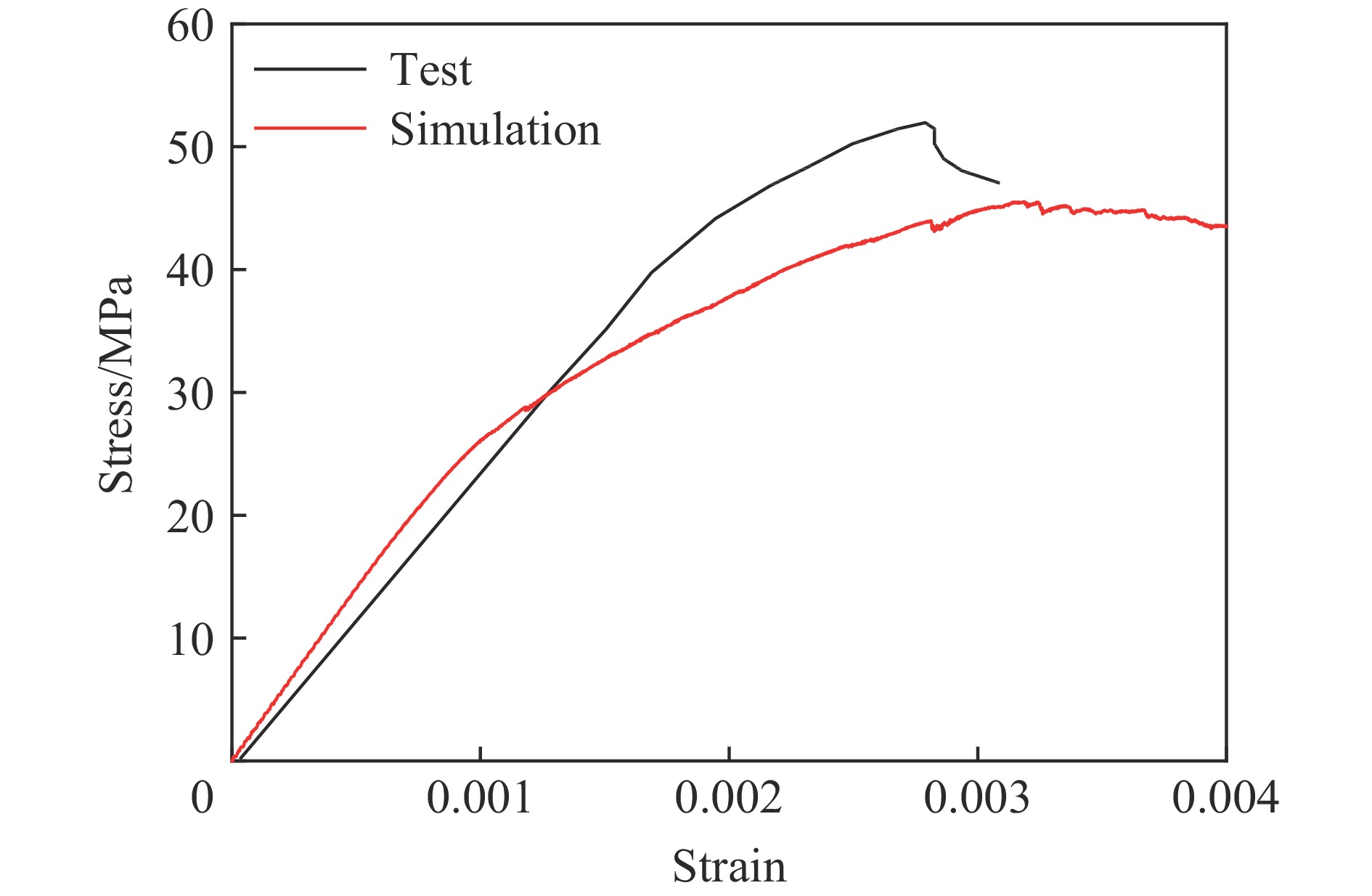
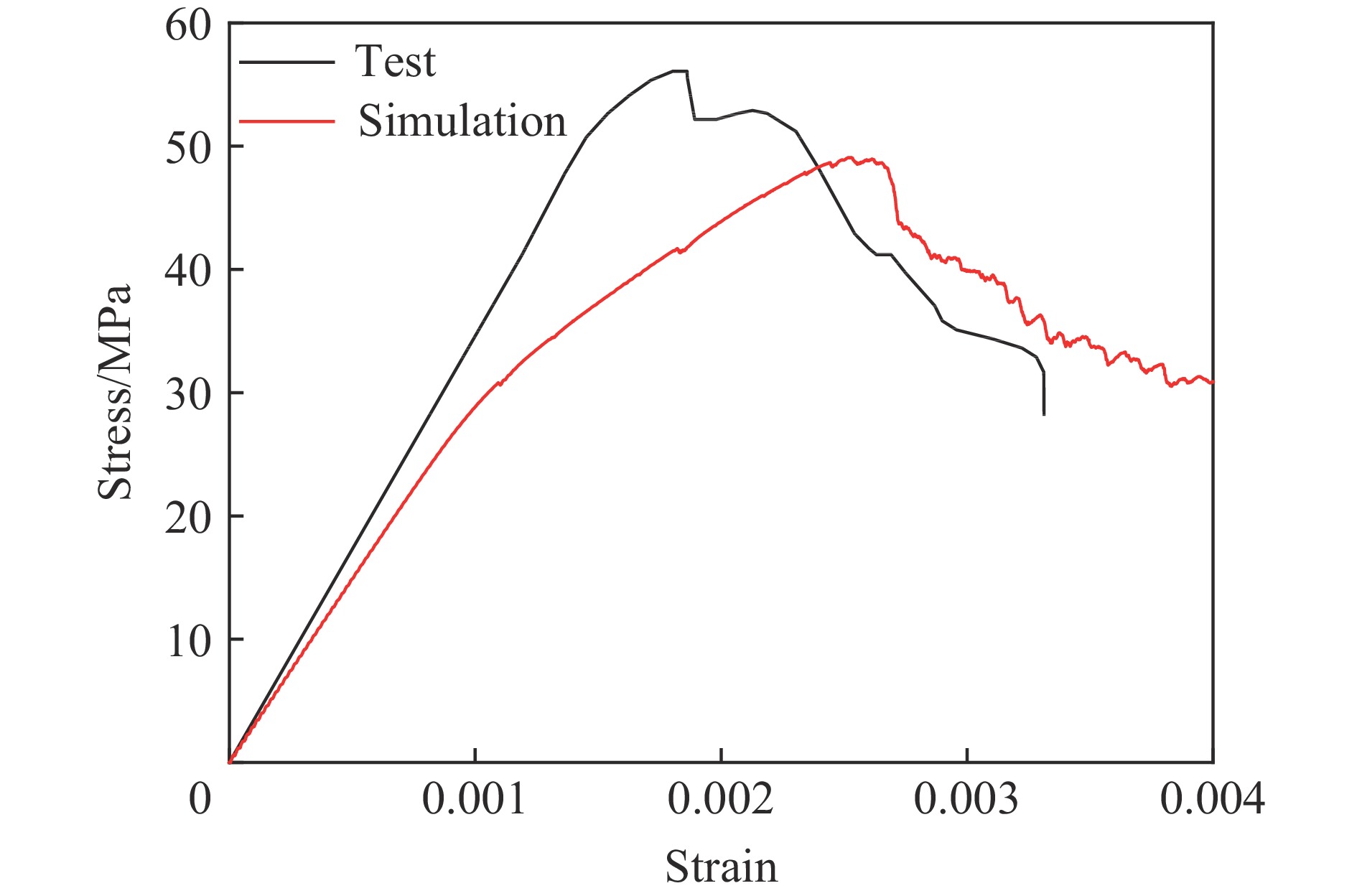
图9~图12对比了准静态试验与数值模拟得到的试件应力-应变曲线,可以看出,各配比混凝土单轴压缩强度的预测结果均与试验数据吻合较好,峰值应力的最大相对误差为15%。
进一步对比SHPB试验[10]中反射波和透射波引起的入射杆和透射杆上的应变时程
εR(t) 和εT(t) ,以及试件材料的动态应力-应变曲线。根据一维弹性波理论[26],试件的动态应力σs(t) 和动态应变εs(t) ,以及应变率˙εs(t) 为{σs(t)=EA0εT(t)/Asεs(t)=2C0∫t0[εI(t)−εT(t)]dt/ls˙εs(t)=2C0[εI(t)−εT(t)]/ls (21) 式中:E、A0和C0=5172 m/s分别为SHPB杆的弹性模量、横截面面积和弹性波波速;As和ls分别为试件的横截面面积和初始长度。上述公式适用的前提条件是试件达到应力平衡状态,即:
εT=εI+εR (22) 式中:
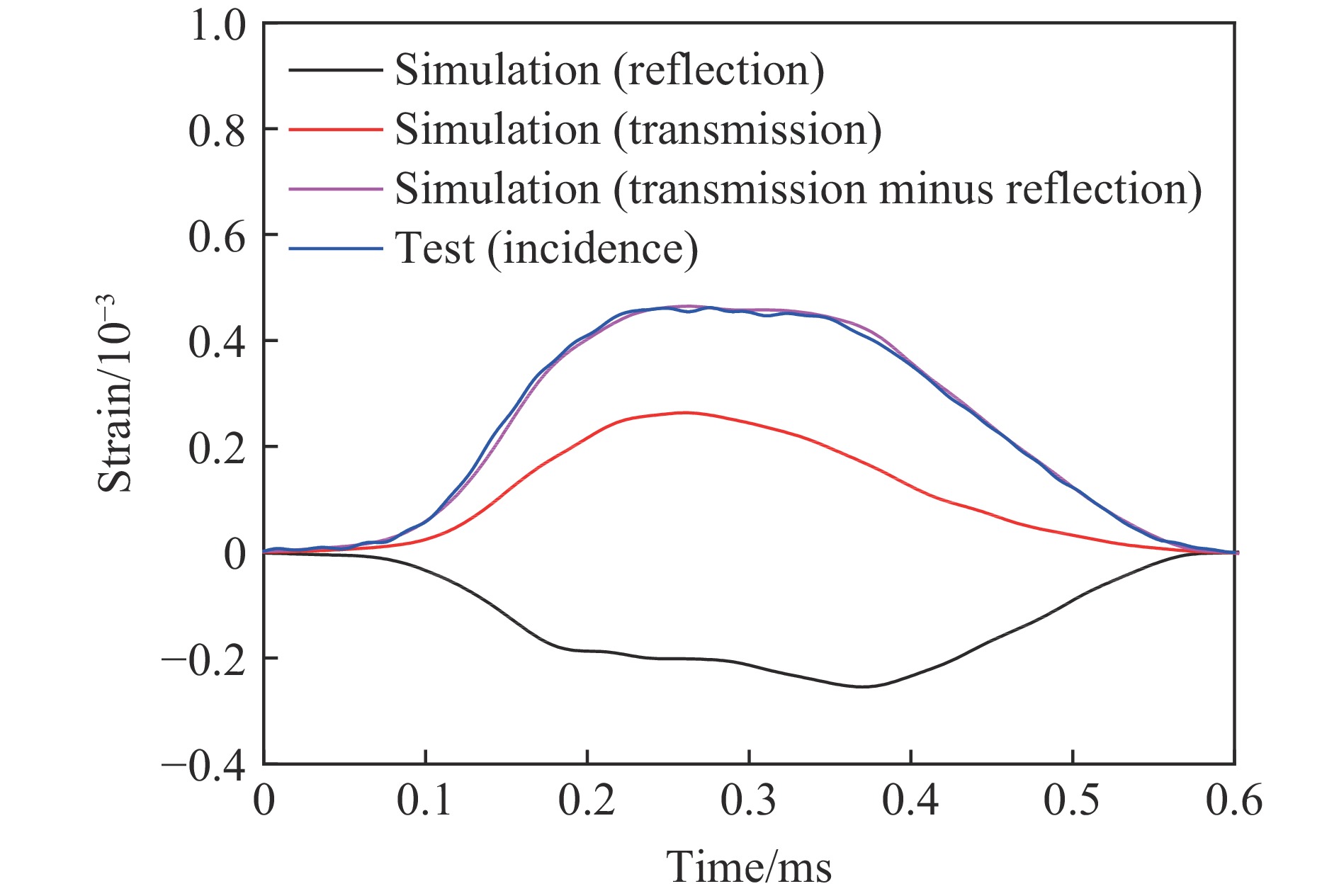
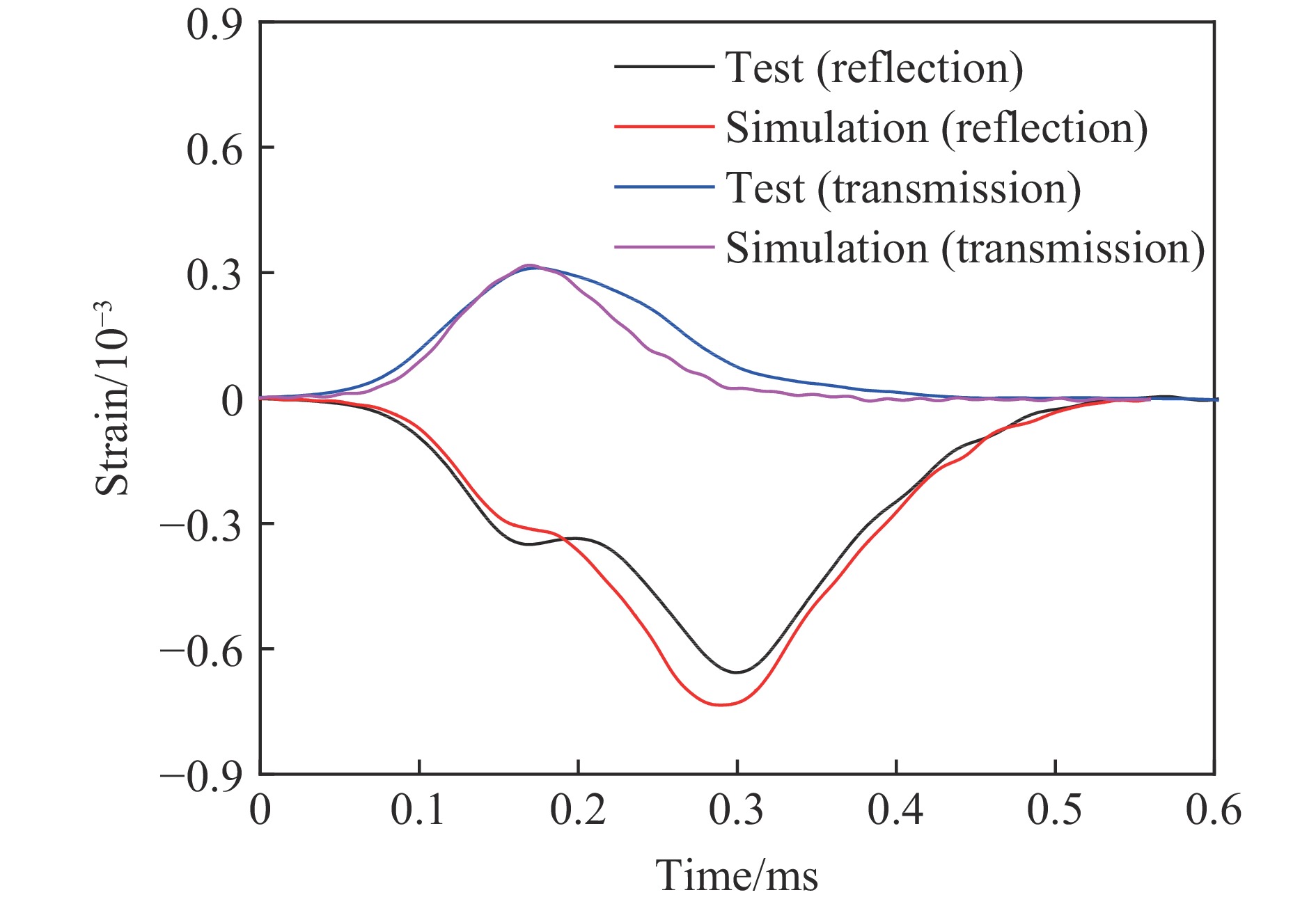
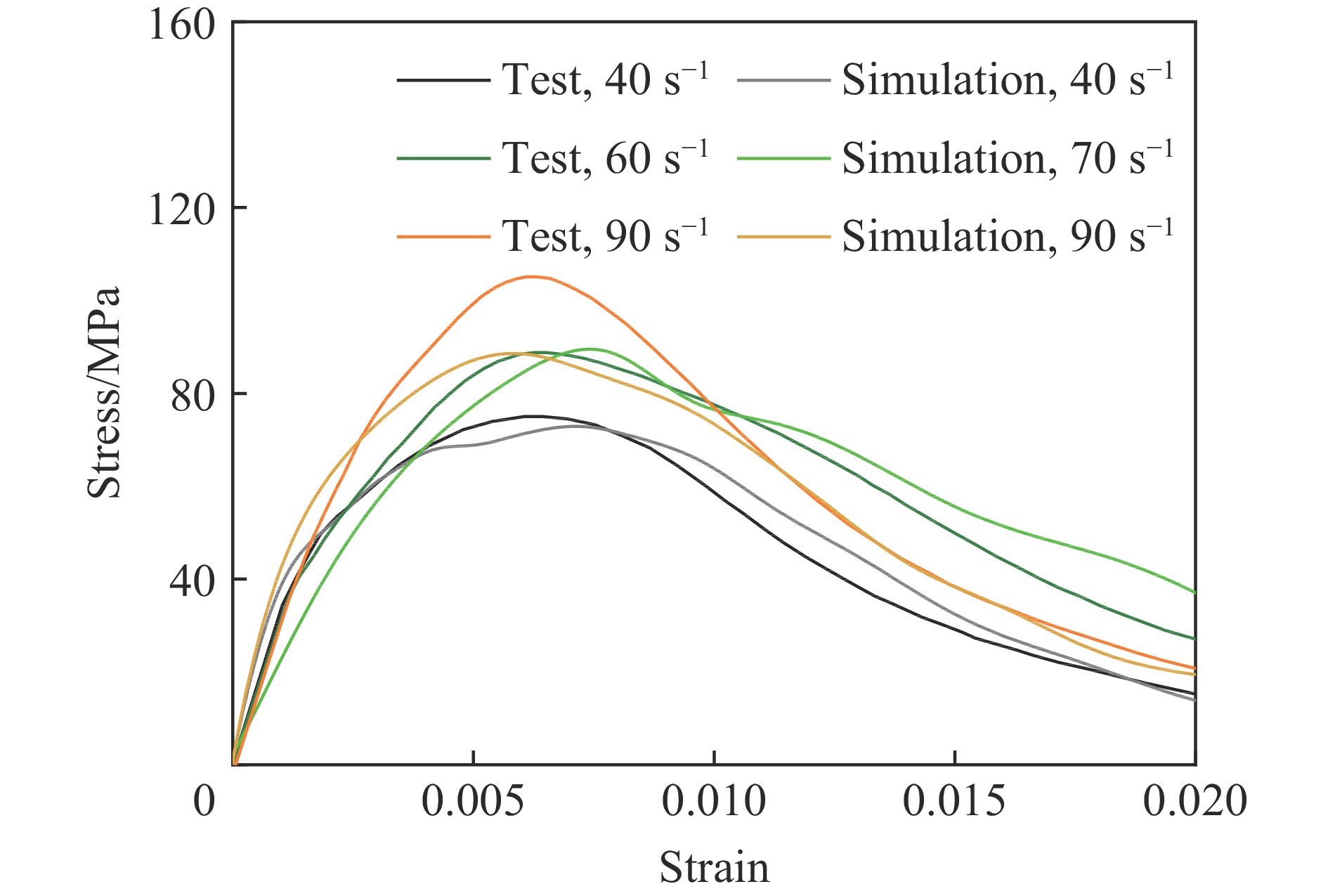
εI 为入射波在入射杆上引起的应变时程。以试件G12应变率为55 s−1的试验工况为例,如图13所示,数值模拟中透射波和反射波之差与试验入射波应变时程曲线基本重合,说明建立的SHPB有限元模型满足应力平衡要求。本文应变率取应变率平台段初始至试件达到最大应力范围内的平均应变率,如图14所示。图15~图18给出了砂浆和3种骨料粒径混凝土典型应变率下试验与模拟得到的入射杆和透射杆上的反射(负)和透射(正)应变时程对比结果,其中工况编号M-65 s−1表示纯砂浆试件且应变率为65 s−1。可以看出试验和模拟得到的波形接近,透射应变峰值最大误差小于15%,且反射波平台段数值和出现时刻均与试验接近。图19~图22进一步对比了各试件的动态应力-应变曲线,可以看出预测结果和试验数据吻合较好,峰值应力的最大相对误差为18%。
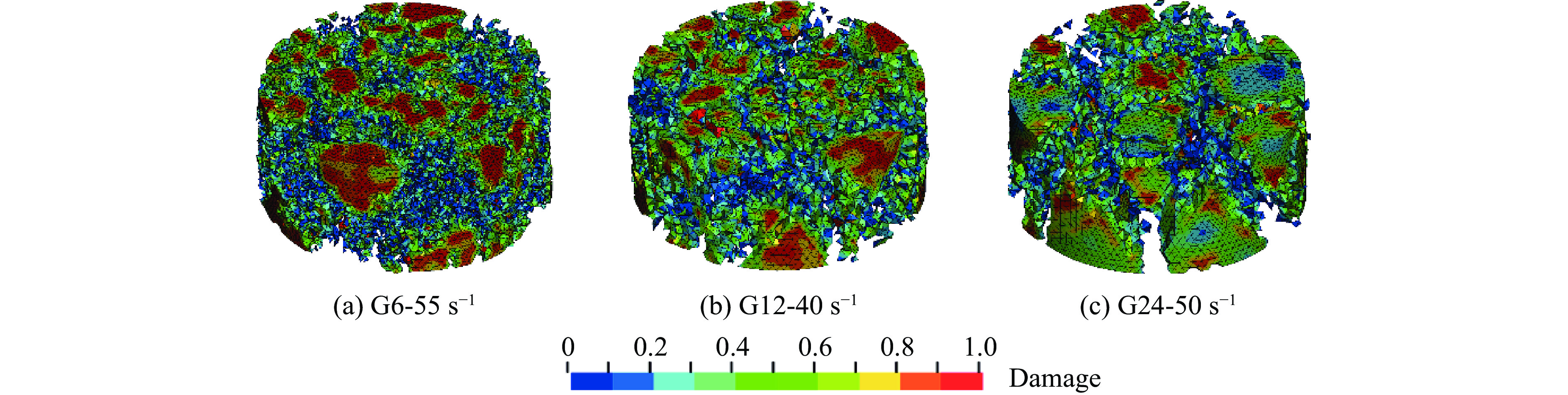
图23和图24给出了数值模拟得到的试件破坏模式。可以看出:随着应变率增大,砂浆和混凝土试件破坏更加严重。当应变率低于和高于60 s−1时试件分别呈现碎裂和粉末化破坏模式,这与Lv等[27]的SHPB试验结果吻合。图24给出了不同骨料粒径混凝土的破坏模式。可以看出,在几乎相同应变率下,小骨料粒径混凝土中骨料数量更多,砂浆和骨料的交界面更复杂,将混凝土分割成较多小区域,由于大部分裂缝均沿骨料和砂浆界面发展,混凝土碎裂成更小块。
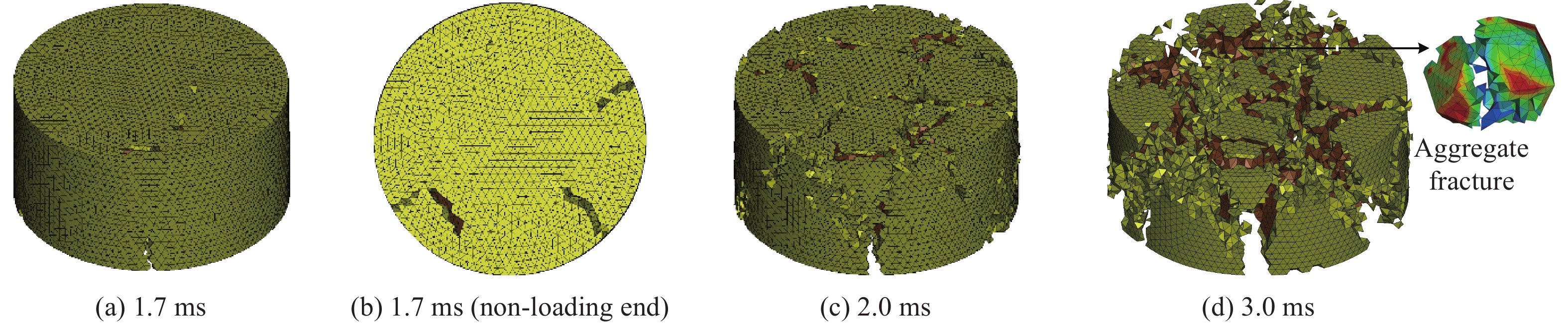
图25给出了应变率为50 s−1时G24试件不同时刻的破坏过程。可以看出:裂缝从混凝土试件非加载端角部开始发展直至贯通,且破坏均始于薄弱的ITZ区域。在动态压缩荷载下,裂缝来不及寻找薄弱区域开展,会同时经过砂浆和坚硬的骨料,导致砂浆开裂和骨料断裂,如图25(d)所示,引起混凝土动态强度提高,与Al-Salloum等[28]试验结论一致。
综上,通过对比砂浆和不同粗骨料粒径混凝土试件的SHPB试验数据以及数值仿真结果,包括杆上应变时程、试件材料动态应力-应变曲线以及试件的损伤破坏模式,验证了建立的混凝土3D细观有限元模型、参数取值和数值仿真方法对于描述混凝土动态压缩行为的准确性。
4. 参数影响分析
本节基于上述验证的混凝土3D细观模型和数值仿真方法,进一步讨论粗骨料粒径、体积率和类型对混凝土动态压缩应力-应变曲线的影响。
4.1 骨料粒径
以文献[10]试验中粗骨料体积率30%的工况为基准工况,保持粗骨料体积率不变,分别了开展骨料粒径范围为4~8、10~14和22~26 mm的混凝土试件的SHPB模拟。图26分别给出了应变率约为40、55和70 s−1时相应的混凝土动态应力-应变曲线。可以看出:随着骨料粒径变大,混凝土动态压缩强度先变大后变小;混凝土粗骨料最大粒径从8 mm增大到14和26 mm时,其动态压缩强度分别提高了17.3%和20.8%(应变率为40 s−1),6.7%和10.7%(应变率为55 s−1),以及27.5%和30.5%(应变率为70 s−1),这与王江波等[10]试验结论一致。其原因在于随着粗骨料粒径的逐渐增大,骨料颗粒对裂缝的阻碍作用增大,导致材料消耗的能量变多,从而表现出其动态强度增大;当粗骨料粒径进一步增大时,混凝土材料在细观尺度上的不均匀性进一步加剧,从而导致其宏观上动态强度的降低。
4.2 骨料体积率
以王江波等[10]试验中粗骨料粒径范围为10~14 mm的工况为基准工况,保持粗骨料粒径不变,分别开展了骨料体积率为20%、30%和40%的混凝土试件的SHPB模拟,其动态应力-应变曲线如图27所示。可以看出:骨料体积率在20%~40%范围变化时,骨料体积率越大,混凝土动态强度越高;骨料体积率从20%增加到30%和40%时,其动态压缩强度分别提高了10.2%和11.7%(应变率为40 s−1),7%和9.4%(应变率为55 s−1),以及7.5%和10.3%(应变率为90 s−1),这与苏新春等[29]试验结论一致。其原因在于随着骨料体积率增大,裂缝经过的骨料变多,其消耗的能量增大,从而导致其动态强度增大。
4.3 骨料类型
以王江波等[10]试验中粗骨料粒径范围和体积率分别为10~14 mm和30%的工况为基准工况,分别开展了骨料类型为石灰岩、花岗岩和玄武岩的混凝土试件的SHPB模拟。需要指出的是,考虑到上述骨料模型参数的获取,本节采用了Holmquist-Johnson-Cook材料模型[30]描述骨料的力学行为,材料参数见表2[31-32]所示。图28分别给出了三种应变率下相应的混凝土动态应力-应变曲线。可以看出:玄武岩骨料混凝土的动态压缩强度分别比石灰岩和花岗岩骨料混凝土提高了9%和2.4%(应变率为35 s−1)、15.2%和7.1%(应变率为55 s−1)以及21.6%和4.7%(应变率为80 s−1),即混凝土动态压缩强度随粗骨料强度的增加而提高,这与Zhang等[33]的试验结论一致。其原因在于,相对于石灰岩(60 MPa)和花岗岩(154 MPa)骨料强度,玄武岩骨料强度较高(200 MPa),动态荷载下使其断裂需要消耗更多的能量,因此玄武岩骨料对混凝土动态强度的提高作用最大。
岩石 ρ0/(kg·m−3) fc/MPa G/GPa T/MPa A0 B0 石灰石[31] 2300 60 10.1 4 0.55 1.23 花岗岩[31] 2660 154 28.7 12.2 0.3 2.5 玄武岩[32] 2800 200 25.2 14.65 0.79 2.5 N σ∗max C0 ˙ε0 D1 D2 ef,min 0.89 20 0.0097 1×10−6 0.04 1 0.01 0.79 15 0.0097 1×10−6 0.04 1 0.01 0.7 15 0.007 1×10−6 0.04 1 0.01 Pc/MPa Pl/GPa K1/GPa K2/GPa K3/GPa μc μl 20 2 39 −223 550 0.00125 0.174 51 1.2 12 25 42 0.00162 0.012 67.7 1.2 12 25 42 0.0012 0.012 注:ρ0为密度,fc为压缩强度,G为剪切模量,T为最大拉伸静水压力,A0、B0、N、σ∗max、C0为强度面参数,˙ε0为应变率效应参数,D1、D2、ef,min为损伤参数,Pc、Pl、K1、K2、K3、μc、μl为状态方程参数。 5. 结 论
本文通过提出一种混凝土3D细观有限元建模方法,对动态荷载作用下混凝土的压缩行为开展了数值仿真分析,主要工作和结论有:
(1)通过传统的“生成-投放”法生成粒径、形状和空间分布均随机的凸多面体骨料模型,并通过提出的骨料重力沉降和粒径缩放方法,实现了粗骨料体积率在50%范围内可调控;
(2)采用四面体网格划分砂浆和骨料以表征其真实形状;采用等效于零厚度粘结单元的粘结接触表征ITZ,解决了20~50 μm厚度ITZ的网格划分问题;采用RHT材料模型描述砂浆和骨料的力学行为和损伤演化,建立了混凝土3D细观有限元模型;
(3)基于建立的混凝土3D细观模型,对动态压缩荷载作用下混凝土试件的力学行为开展了有限元模拟;通过与纯砂浆和不同粗骨料粒径混凝土试件的SHPB试验数据对比,包括杆上应变时程、试件材料动态应力-应变曲线以及试件的损伤破坏模式,验证了建立的混凝土3D细观有限元模型、参数取值和数值仿真方法对于描述混凝土动态压缩行为的准确性;
(4)基于验证的混凝土3D细观模型和数值仿真方法,开展的骨料的参数影响分析,得出随粗骨料粒径增大,混凝土动态压缩强度先增大后减小;粗骨料体积率越高,混凝土动态压缩强度越大;混凝土动态压缩强度随粗骨料强度的增加而提高,并得到已有试验[10, 29, 33]的验证。
-
表 1 砂浆的RHT模型参数
Table 1. RHT model parameters of mortar
参数类型 参数 符号 取值 参数类型 参数 符号 取值 基本强度参数 拉压强度比 f*t 0.18 失效面参数 失效面参数 Af 1.6 剪压强度比 f∗s 0.1 失效面指数 N 0.61 弹性屈服面参数 压缩屈服面参数 g∗c 0.53 拉压子午比 Q0 0.6805 拉伸屈服面参数 g∗t 0.7 罗德角相关系数 BL 0.0105 残余强度面参数 残余强度参数 Ar 1.4 压缩应变率指数 βc 5.64×10−3 残余强度指数 nr 0.61 拉伸应变率指数 βt 0.02 硬化段参数 剪切模量缩减系数 ξ 0.9 参考压缩应变率 ˙εc0 3×10−5 s−1 软化段参数 损伤参数 D1 0.02 参考拉伸应变率 ˙εt0 3×10−6 s−1 损伤指数 D2 1 过渡压缩应变率 ˙εcp 30 s−1 最小失效应变 εmp 0.01 过渡拉伸应变率 ˙εtp 30 s−1 岩石 ρ0/(kg·m−3) fc/MPa G/GPa T/MPa A0 B0 石灰石[31] 2300 60 10.1 4 0.55 1.23 花岗岩[31] 2660 154 28.7 12.2 0.3 2.5 玄武岩[32] 2800 200 25.2 14.65 0.79 2.5 N σ∗max C0 ˙ε0 D1 D2 ef,min 0.89 20 0.0097 1×10−6 0.04 1 0.01 0.79 15 0.0097 1×10−6 0.04 1 0.01 0.7 15 0.007 1×10−6 0.04 1 0.01 Pc/MPa Pl/GPa K1/GPa K2/GPa K3/GPa μc μl 20 2 39 −223 550 0.00125 0.174 51 1.2 12 25 42 0.00162 0.012 67.7 1.2 12 25 42 0.0012 0.012 注:ρ0为密度,fc为压缩强度,G为剪切模量,T为最大拉伸静水压力,A0、B0、N、σ∗max、C0为强度面参数,˙ε0为应变率效应参数,D1、D2、ef,min为损伤参数,Pc、Pl、K1、K2、K3、μc、μl为状态方程参数。 -
[1] GROTE D L, PARK S W, ZHOU M. Dynamic behavior of concrete at high strain rates and pressures: I. experimental characterization [J]. International Journal of Impact Engineering, 2001, 25(9): 869–886. DOI: 10.1016/S0734-743X(01)00020-3. [2] KLEPACZKO J R, BRARA A. An experimental method for dynamic tensile testing of concrete by spalling [J]. International Journal of Impact Engineering, 2001, 25(4): 387–409. DOI: 10.1016/S0734-743X(00)00050-6. [3] BRARA A, CAMBORDE F, KLEPACZKO J R, et al. Experimental and numerical study of concrete at high strain rates in tension [J]. Mechanics of Materials, 2001, 33(1): 33–45. DOI: 10.1016/S0167-6636(00)00035-1. [4] DIAMARUYA M, KOBAYASHI H, NONAKA T. Impact tensile strength and fracture of concrete [J]. Journal de Physique Archives IV, 1997, 7(C3): 253–258. DOI: 10.1051/jp4:1997345. [5] REINHARDT H W, ROSSI P, VAN MIER J G M. Joint investigation of concrete at high rates of loading [J]. Materials and Structures, 1990, 23(3): 213–216. DOI: 10.1007/bf02473020. [6] TEDESCO J W, ROSS C A, MCGILL P B, et al. Numerical analysis of high strain rate concrete direct tension tests [J]. Computers & Structures, 1991, 40(2): 313–327. DOI: 10.1016/0045-7949(91)90357-R. [7] WEERHEIJM J, VAN DOORMAAL J C A M. Tensile failure of concrete at high loading rates: new test data on strength and fracture energy from instrumented spalling tests [J]. International Journal of Impact Engineering, 2007, 34(3): 609–626. DOI: 10.1016/j.ijimpeng.2006.01.005. [8] KOLSKY H. An investigation of the mechanical properties of materials at very high rates of loading [J]. Proceedings of the Physical Society, Section B, 1949, 62(11): 676–700. DOI: 10.1088/0370-1301/62/11/302. [9] HAO Y, HAO H, JIANG G P, et al. Experimental confirmation of some factors influencing dynamic concrete compressive strengths in high-speed impact tests [J]. Cement and Concrete Research, 2013, 52: 63–70. DOI: 10.1016/j.cemconres.2013.05.008. [10] 王江波, 丁俊升, 王晓东, 等. 粗骨料粒径对混凝土动态压缩行为的影响研究 [J]. 爆炸与冲击, 2022, 42(2): 023101. DOI: 10.11883/bzycj-2021-0147.WANG J B, DING J S, WANG X D, et al. Effect of coarse aggregate size on the dynamic compression behavior of concrete [J]. Explosion and Shock Waves, 2022, 42(2): 023101. DOI: 10.11883/bzycj-2021-0147. [11] 郭瑞奇, 任辉启, 张磊, 等. 基于混凝土细观骨料模型的SHPB仿真模拟研究 [J]. 振动与冲击, 2019, 38(22): 107–116. DOI: 10.13465/j.cnki.jvs.2019.22.015.GUO R Q, REN H Q, ZHANG L, et al. Simulation for SHPB tests based on a mesoscopic concrete aggregate model [J]. Journal of Vibration and Shock, 2019, 38(22): 107–116. DOI: 10.13465/j.cnki.jvs.2019.22.015. [12] ZHOU X Q, HAO H. Modelling of compressive behaviour of concrete-like materials at high strain rate [J]. International Journal of Solids and Structures, 2008, 45(17): 4648–4661. DOI: 10.1016/j.ijsolstr.2008.04.002. [13] PAJĄK M, BARANOWSKI P, JANISZEWSKI J, et al. Experimental testing and 3D meso-scale numerical simulations of SCC subjected to high compression strain rates [J]. Construction and Building Materials, 2021, 302: 124379. DOI: 10.1016/j.conbuildmat.2021.124379. [14] LV T H, CHEN X W, DENG Y J, et al. Further numerical investigation on concrete dynamic behaviors with considering stress non-equilibrium in SHPB test based on the waveform features [J]. Acta Mechanica Sinica, 2020, 36(4): 873–886. DOI: 10.1007/s10409-020-00974-z. [15] WU Z Y, ZHANG J H, YU H F, et al. Experimental and mesoscopic investigation on the dynamic properties of coral aggregate concrete in compression [J]. Science China Technological Sciences, 2021, 64(6): 1153–1166. DOI: 10.1007/s11431-020-1739-y. [16] ZHOU R X, SONG Z H, LU Y. 3D mesoscale finite element modelling of concrete [J]. Computers & Structures, 2017, 192: 96–113. DOI: 10.1016/j.compstruc.2017.07.009. [17] WANG X F, ZHANG M Z, IVKOV A P. Computational technology for analysis of 3D meso-structure effects on damage and failure of concrete [J]. International Journal of Solids and Structures, 2016, 80: 310–333. DOI: 10.1016/j.ijsolstr.2015.11.018. [18] SHENG P Y, ZHANG J Z, JI Z. An advanced 3D modeling method for concrete-like particle-reinforced composites with high volume fraction of randomly distributed particles [J]. Composites Science and Technology, 2016, 134: 26–35. DOI: 10.1016/j.compscitech.2016.08.009. [19] GRUNWALD C, SCHAUFELBERGER B, STOLZ A, et al. A general concrete model in hydrocodes: verification and validation of the Riedel-Hiermaier-Thoma model in LS-DYNA [J]. International Journal of Protective Structures, 2017, 8(1): 58–85. DOI: 10.1177/2041419617695977. [20] LSTC. LS-DYNA keyword user's manual volume I-II, version R11 [R]. CA, USA: Livermore Software Technology Corporation, 2018. [21] CHEN D, WU H, FANG Q. Simplified micro-model for brick masonry walls under out-of-plane quasi-static and blast loadings [J]. International Journal of Impact Engineering, 2023, 174: 104529. DOI: 10.1016/j.ijimpeng.2023.104529. [22] Federation Internationale du Beton. FIB model code for concrete structures [S]. Switzerland: Comite Euro-International du Beton, 2010. DOI: 10.1002/9783433604090. [23] JIN L, YU W X, DU X L, et al. Meso-scale modelling of the size effect on dynamic compressive failure of concrete under different strain rates [J]. International Journal of Impact Engineering, 2019, 125: 1–12. DOI: 10.1016/j.ijimpeng.2018.10.011. [24] MALEKI M, RASOOLAN I, KHAJEHDEZFULY A, et al. On the effect of ITZ thickness in meso-scale models of concrete [J]. Construction and Building Materials, 2020, 258: 119639. DOI: 10.1016/j.conbuildmat.2020.119639. [25] WANG J M, LI X, JIVKOV A P, et al. Interfacial transition zones in concrete meso-scale models: balancing physical realism and computational efficiency [J]. Construction and Building Materials, 2021, 293: 123332. DOI: 10.1016/j.conbuildmat.2021.123332. [26] CHEN W N, SONG B. Split Hopkinson (Kolsky) bar: design, testing and applications [M]. Beijing: National Defense Industry, 2011. [27] LV T H, CHEN X W, CHEN G. Analysis on the waveform features of the split Hopkinson pressure bar tests of plain concrete specimen [J]. International Journal of Impact Engineering, 2017, 103: 107–123. DOI: 10.1016/j.ijimpeng.2017.01.004. [28] AL-SALLOUM Y, ALMUSALLAM T, IBRAHIM S M, et al. Rate dependent behavior and modeling of concrete based on SHPB experiments [J]. Cement and Concrete Composites, 2015, 55: 34–44. DOI: 10.1016/j.cemconcomp.2014.07.011. [29] 苏新春, 蒋国平. 混凝土材料骨料效应SHPB实验研究 [J]. 四川建材, 2017, 43(10): 22–23. DOI: 10.3969/j.issn.1672-4011.2017.10.011.SU X C, JIANG G P. SHPB experimental study on aggregate effect of concrete materials [J]. Sichuan Building Materials, 2017, 43(10): 22–23. DOI: 10.3969/j.issn.1672-4011.2017.10.011. [30] HOLMQUIST T J, JOHNSON G R, COOK W H. A computational constitutive model for concrete subjected to large strains, high strain rates, and high pressures [C]// Proceedings of the 14th International Symposium on Ballistics. Quebec, Canada: IBC, 1993: 591–600. [31] WANG X H, ZHANG S R, DAI J G, et al. Evaluation of base damage and stability of concrete gravity dam subjected to underwater explosion [J]. Structures, 2022, 38: 1502–1514. DOI: 10.1016/j.istruc.2022.03.012. [32] 宫俊, 吴昊, 方秦, 等. 刚玉骨料超高性能水泥基材料抗侵彻试验和细观数值模拟 [J]. 振动与冲击, 2017, 36(1): 55–63. DOI: 10.13465/j.cnki.jvs.2017.01.008.GONG J, WU H, FANG Q, et al. Test and mesoscale numerical simulation for corundum-aggregate ultra-high performance cementitious composites against projectile penetration [J]. Journal of Vibration and Shock, 2017, 36(1): 55–63. DOI: 10.13465/j.cnki.jvs.2017.01.008. [33] ZHANG W H, ZHANG Y S. Research on the static and dynamic compressive properties of high performance cementitious composite (HPCC) containing coarse aggregate [J]. Archives of Civil and Mechanical Engineering, 2015, 15(3): 711–720. DOI: 10.1016/j.acme.2014.12.006. 期刊类型引用(1)
1. 吴昊,张瑜,程月华,岑国华. 典型战斗部侵彻爆炸下块石混凝土的遮弹层设计. 爆炸与冲击. 2025(04): 111-124 .  本站查看
本站查看其他类型引用(4)
-









 下载:
下载:






















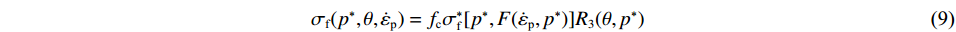














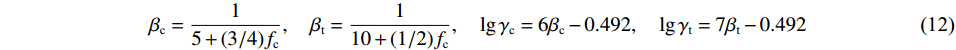
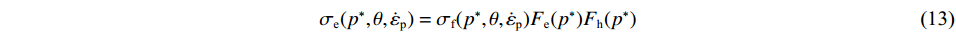



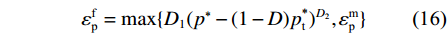



















































 下载:
下载: