Influence of incident angle on precursor wave characteristics at specific thermal-layer temperature
-
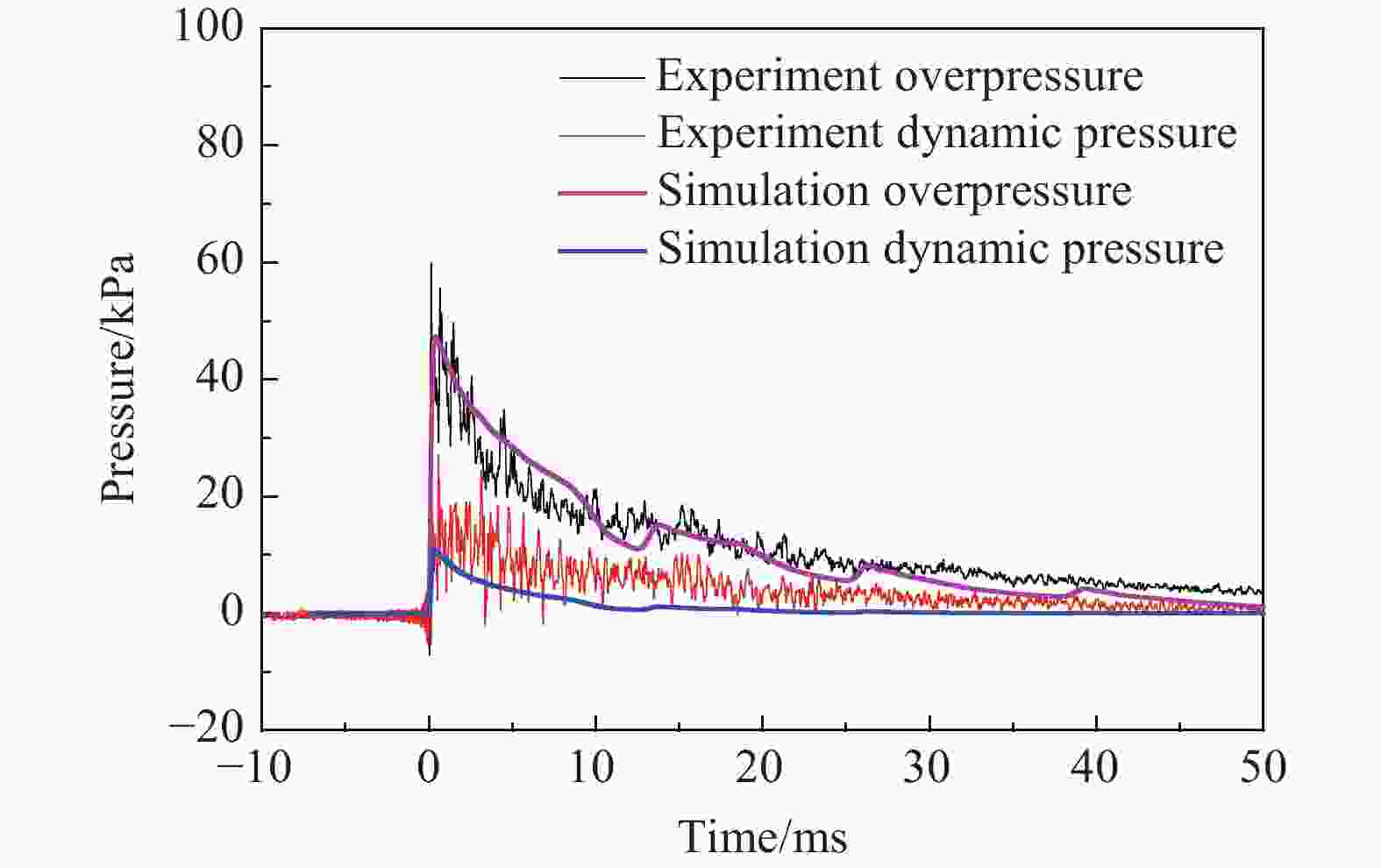
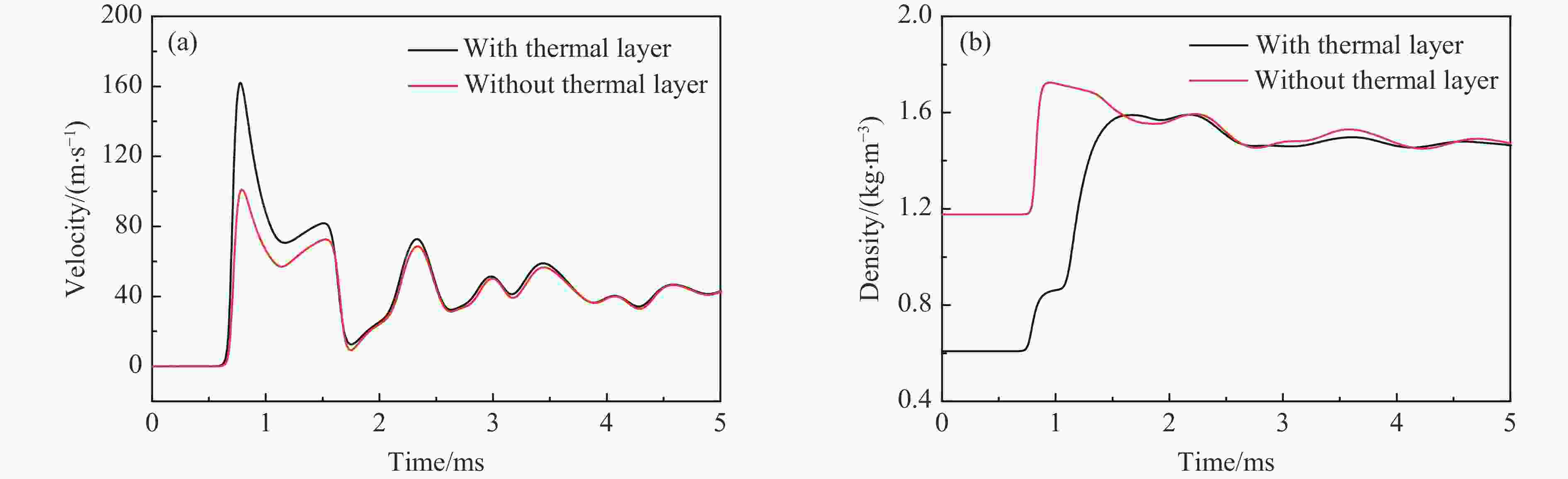
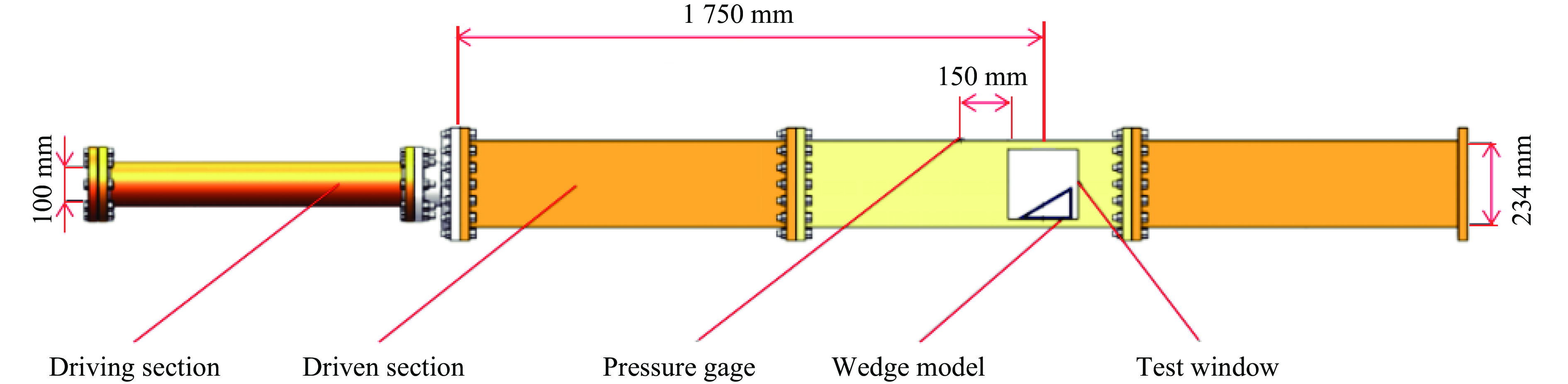
摘要: 空中强爆炸会释放热辐射使地表形成热层，冲击波进入热层后传播速度加快，形成前驱波。冲击波入射角是影响前驱波特性的重要因素，但目前相关工作大多依赖理论推导，实验研究较少。利用爆炸波模拟激波管平台，开展了热层温度为300 ℃时入射角对前驱波形成影响的研究实验，结合实验构型建立了数值仿真模型，并将实验、数值仿真结果与已有理论结果进行了对比。结果表明：实验获得的前驱波形成临界角范围与理论计算结果一致；入射角越大，前驱波超过马赫杆的距离越大，到时提前越多；前驱波会导致超压峰值减小，且随着入射角的增大，超压峰值减小程度先增大后减小；整体上看，前驱波动压峰值随入射角的增大而增大，当入射角达到一定阈值后，动压峰值增大程度开始在一定范围内波动，这是由气流密度和粒子速度的峰值到时不同所导致的；动压冲量的增大程度随入射角的增大逐渐增大。Abstract: An intense explosion in the air releases heat radiation to form a thermal layer on the earth’s surface, and the shock wave propagates faster when it enters the thermal layer, forming a precursor wave. The incidence angle is an important factor affecting the characteristics of the precursor wave, but at present, most of the related work depends on theoretical derivation, and the experimental research is few. The influence of the incident angle on the precursor wave formation at 300 ℃ is studied using an explosion wave simulation shock tube platform. A thick iron plate is heated to 300 ℃ and fixed in the shock tube test section, the surface of which produces a thermal layer of 1 cm thick. The interaction between the shock wave generated by the shock tube and the thermal layer is captured by a high-speed camera. The influence of different incident angles on the precursor wave is studied. A numerical simulation model is established based on the experimental configuration. First, a complete axial symmetric shock tube model is established, and a data monitoring point is set at the position corresponding to the pressure measurement point in the model. Then, a plane model is built. The data of total pressure, static pressure, and total temperature calculated in the first step are the input, and the cloud diagram and pressure curve at the measuring point of the model are the output. The results show that the critical angle range of the precursor wave is consistent with the theoretical results. The greater the angle of incidence, the greater the distance of the precursor wave over the Mach stem, and the earlier the arrival time. The precursor wave will lead to a decrease in the peak overpressure, and as the incident angle increases, the decrease degree of overpressure peak increases first and then decreases. Overall, the peak dynamic pressure increases with the incident angle. When the incident angle reaches a certain threshold, the peak dynamic pressure begins to fluctuate in a certain range, the reason is that the peak arrival time of airflow density and particle velocity are different. The increase degree of dynamic pressure impulse increases with the increase of incident angle.
-
图 4 不同入射角度、有无热层实验纹影图像对比
Figure 4. Comparison of experimental schlieren images with thermal layer with ones without thermal layer at different incident angles
图 5 前驱波超前马赫杆的距离示意图
Figure 5. Diagram of the distance of the precursor wave leading the Mach stem
图 6 在完整二维轴对称模型中截取部分模型
Figure 6. Interception of the partial model from a complete two-dimensional axisymmetrical model
图 7 部分模型中添加斜面及高温热层
Figure 7. Addition of inclined plane and high-temperature thermal layer in the partial model
图 8 入射波超压和动压随时间的演化
Figure 8. Evolution of incident overpressure and dynamic pressure with time
图 9 有无热层时压力云图数值仿真结果
Figure 9. Numerically-simulated pressure clouds with and without thermal layer
图 10 入射角对冲击波到时及其提前程度的影响
Figure 10. Influences of incident angle of shock wave on arrival time and its advance degree
图 11 入射角对超压峰值及其减小程度的影响
Figure 11. Influence of incident angle of shock wave on peak overpressure and its decreasing degree
图 12 入射角对动压峰值及其增大程度的影响
Figure 12. Influence of incident angle of shock wave on peak dynamic pressure and its increase degree
图 13 入射角为60°时测点的粒子速度和气流密度随时间的演化
Figure 13. Evolutions of particle velocity and airflow density with time at the measured point when the incident angle of shock wave is 60°
图 14 入射角对动压冲量及其增大程度的影响
Figure 14. Influences of incident angle of shock wave on dynamic pressure impulse and its increase degree
表 1 实验条件
Table 1. Experimental conditions
实验
编号入射冲击波
压力/kPa入射角
β/(°)温度/
℃有无
热层1-1 50 75 15 无 1-2 300 有 2-1 50 60 15 无 2-2 300 有 3-1 50 45 15 无 3-2 300 有 4-1 50 30 15 无 4-2 300 有 
下载: 导出CSV
表 2 不同入射角时前驱波、马赫波波速及波速差
Table 2. Precursor and Mach wave velocities as well as their differences at different incident angles
β/(°) vp/(m∙s−1) vM/(m∙s−1) Δv/(m∙s−1) 75 493.36 447.53 45.83 60 500.77 478.98 21.79
下载: 导出CSV
-
[1] GLASSTONE S, DOLAN P J. The effects of nuclear weapons: TID-28061 [R]. 3rd ed. Washington: Department of Defense, 1977. [2] ARTEM’EV V I, BERGEL’SON V I, MEDVEDYUK S A, et al. Amplification of intense blast pressure in a medium with this rarefied channels [J]. Fluid Dynamics, 1996, 31(1): 121–126. DOI: 10.1007/BF02230756. [3] ETHRIDGE N H, KEEFER J H, CREPEAU J E, et al. Real surface (non-ideal) effects on nuclear explosion airblast from PRISCILLA-type events, part 1: comparison and evaluation of ideal and non-ideal airblast from priscilla computations; and part 2: sharc hydrocode calculations of the priscilla event (phase 1). Final report, 12 March 1992-30 May 1995: AD-A-302079/9/XAB [R]. Aberdeen: Applied Research Associates, Inc. , 1995. [4] FRY M A, KAMATH P, BOOK D L. Priscilla calculations and comparison with data: AD-A155 666 [R]. Washington: Naval Research Laborarory, 1985. [5] SWIFT L M, SACHS D C, KRIEBEL A R. Air-blast phenomena in the high-pressure region: WT-1403 [R]. Menlo Park, California: Stanford Research Institute, 1960. [6] BRYANT E J , ALLEN F. Dynamic pressure impulse for near ideal and non-ideal blast waves: DNA-82-C-0287 [R]. Alexandria, VA: Defense Nuclear Agency, 1983. [7] NEEDHAM C E. Blast waves [M]. Berlin, Heidelberg: Springer, 2010. [8] ZASLAVSKII B I, MOROZKIN S Y, PROKOF’EV A A, et al. Flow of a planar shock wave around a thermal layer at a rigid wall [J]. Journal of Applied Mechanics and Technical Physics, 1990, 31(3): 354–361. DOI: 10.1007/BF00864563. [9] 乔登江. 核爆炸物理概论 [M]. 北京: 国防工业出版社, 2003. [10] 贾雷明, 田宙. 平面冲击波与热层作用数值研究 [J]. 现代应用物理, 2015, 6(4): 305–311. DOI: 10.3969/j.issn.2095-6223.2015.04.013.JIA L M, TIAN Z. Numerical simulation of the interactions between planar shocks and thermal layer [J]. Modern Applied Physics, 2015, 6(4): 305–311. DOI: 10.3969/j.issn.2095-6223.2015.04.013. [11] GRIFFITH W C. Interaction of a shock wave with a thermal boundary layer [J]. Journal of the Aeronautical Sciences, 1956, 23(1): 16–22. DOI: 10.2514/8.3495. [12] GION E J. Plane shock interacting with thermal layer [J]. Physics of Fluids, 1977, 20(4): 700–702. DOI: 10.1063/1.861928. [13] BEN-DOR G. Shock wave reflection phenomena [M]. 2nd ed. Berlin: Springer, 2007. DOI: 10.1007/978-3-540-71382-1. [14] 王福军. 计算流体动力学分析: CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004. [15] NEEDHAM C E, EKLER R G, KENNEDY L W. Extended desert calculation results with comparisons to PRISCILLA experimental data and a near-ideal calculation: ARL-CR-235 [R]. Albuquerque: S-Cubed, 1995. [16] EKLER R G, NEEDHAM C E, KENNEDY L W. Extended grassland calculation results with comparisons to PRISCILLA experimental data and a near-ideal calculation: AD-A-298081/1/XAB [R]. Albuquerque: S-Cubed, 1995. -
计量
- 文章访问数: 129
- HTML全文浏览量: 29
- PDF下载量: 38
- 被引次数: 0