Response analysis of liquid sloshing in a tank with rigid baffles
-
摘要: 部分充液罐体内的液体在外部激励的作用下容易出现晃动现象,由液体晃动产生的附加力和力矩会对载液罐车产生不利影响。为了避免液罐车制动时其罐内液体产生较大幅度的晃动,提出了几种类型的防波板,并研究了防波板及其几何参数对液罐车内液体晃动的影响。首先,建立了基于有限体积法的液体晃动的数值模型。其次,对液体晃动现象进行了一系列的实验,通过将实验获得的液面波形与同等条件下数值模拟获得的结果进行对比,验证数值模型的有效性。最后,将验证后的数值模型用于分析防波板的几何参数对液体晃动响应的影响。研究结果表明,开孔防波板不仅可以有效降低罐内晃动响应参数的峰值,还可以明显缩短罐内晃动液体达到稳定的时间;防波板的开孔位置和孔的数量在车辆制动过程中对罐体内液体晃动引起的纵向力的峰值影响差别不大,但是对液体晃动引起的俯仰力矩的峰值的影响比较明显;晃动响应参数峰值的下降率会随着充液高度的增加呈先下降后上升的趋势,液体晃动引起的俯仰力矩的峰值取得最大值时,防波板对罐体内的液体晃动的抑制效果最差。Abstract: The liquid in partially filled tanks is prone to slosh under external excitation, and the additional forces and moments generated by liquid sloshing can have adverse effects on tank trucks. In order to avoid significant sloshing of the liquid in the tank when the tank truck brakes, several types of baffles were proposed, and the influence of baffles and their geometric parameters on the liquid sloshing inside the tank truck was studied. Firstly, a numerical model of liquid sloshing based on the finite volume method was established. Secondly, a series of liquid sloshing experiments were conducted. The effectiveness of the numerical model was verified by comparing the free surface waveforms obtained from the experiments at different times with those obtained from numerical simulations under the same conditions. Finally, the validated numerical model was used to analyze the influence of the geometric parameters of the baffle on the liquid sloshing response parameters under different liquid-filling conditions. The research results indicate that the perforated baffle can not only effectively suppress the peak of the sloshing response parameters in the tank but also significantly shorten the time for liquid sloshing to reach stability. The position and number of baffle orifices have little effect on the peak longitudinal force caused by liquid sloshing during vehicle braking, while the peak pitch moment is more significantly affected by the geometric parameters of the baffle. By studying liquid sloshing in the tank at different filling heights, it is found that the decrease rate of the peak value of the sloshing response parameter will first decrease and then increase with the increase of the filling height. When the peak value of pitch moment reaches its maximum value, the baffle has the worst suppression effect on liquid sloshing in a partially filled tank.
-
Key words:
- liquid sloshing /
- tank truck /
- baffle /
- longitudinal force /
- pitch moment
-
充液罐体内的液体晃动现象广泛存在于海洋运输[1-2]、航空航天[3-5]和公路运输[6-8]等领域。当罐体运动状态发生改变时,内部液体会发生复杂的运动,由此产生的晃动力将对罐体结构以及罐车运行的稳定性产生不利影响[9]。
目前研究液体晃动主要有数值模拟法、实验法[10]和解析法[11]。其中数值模拟方法包括有限体积法(finite volume method,FVM)、有限元法(finite element method,FEM)、有限差分法(finite difference method,FDM)、光滑粒子流体动力学(smoothed particle hydrodynamics,SPH)方法、半隐式运动粒子法(moving particle method,MPS)和格子玻尔兹曼方法(lattice Boltzmann method,LBM)等。如Fan等[12]采用FVM研究了等比例缩小的船体模型在不同外部激励条件下的俯仰运动和横摇运动,发现船体在无装载和较高充液比情况下,其俯仰角度变化受波长的影响较小,同时通过研究不同载液船体的运动,发现改变船体横摇的固有频率会影响载液船体横摇的幅度。Ye等[13]利用FEM研究了带防波板的圆柱形罐体内的液体晃动特性,结果表明,防波板上孔的几何尺寸和分布位置对罐内液体的晃动特性影响较大。Shao等[14]采用SPH方法研究了水平激励作用下隔板对罐内液体晃动的影响,结果表明,相较于水平防波板,竖直隔板对波高的抑制效果更明显。Bai等[15]通过FDM建立了海浪冲击下的船舶模型,发现共振频率下激发的自由液面高度会随着充液高度的增加而下降。Wen等[16]采用改进的MPS研究了充液罐内剧烈的液体晃动,发现晃动程度越剧烈,空穴或气泡现象[17-18]对晃动液体的能量耗散越明显。Ma等[19]采用LBM研究了双竖直防波板对液体晃动的影响,发现防波板等间距布置在罐体内时对液体的晃动幅值的抑制更有效。
抑制液体晃动的措施主要有隔板、防波板和柔性板。Rakheja等[20]研究了车辆转弯过程中带有隔板的罐体的侧翻极限,发现由于罐内隔板的存在,充液比为50%时液罐车与刚性货车的侧翻极限非常接近。Fang等[21]研究了地震激励下环形防波板对液体晃动的影响,发现水平环形防波板的宽度与罐体直径的比值为0.125~0.175、防波板的布置高度与罐体高度的比值为0.125~0.220时,防波板可以有效抑制晃动液体的波高。Wang等[22]研究了刹车激励下组合防波板对液体晃动的影响,发现组合防波板结构可以有效地降低晃动力的峰值并削弱晃动液体对罐壁的冲击,且在装载液体总质量一定的前提下,充液比越高,罐车的稳定性越好。Xue等[23]研究了顶部与自由液面重合的悬浮防波板在罐内不同位置对液体晃动的影响,结果表明,在防波板靠近罐体中心时,可以通过降低液体的流速实现对罐壁附近波高的抑制。曾宪君等[24]研究了横摇激励下防波板对贮箱内液体晃动的影响,发现在贮箱内部两侧安装防波板可以有效降低晃动液体的质心高度和作用在箱体壁面上的压力。Jin等[25]研究了带有水平防波板的矩形罐内的液体晃动,结果表明,等宽度与不等宽度的防波板都具有更好的减小罐体受力的能力,但是较宽的防波板对罐壁受到的液体冲击力抑制效果更好。Zhang等[26]对布置在燃油箱内不同高度和不同开孔形状的防波板进行了研究,发现防波板上的圆形孔对罐体中心点处的晃动压力有明显的抑制作用。Tsao等[27]研究了脉冲激励下多孔防波板对充液罐内液体晃动的影响。在脉冲激励作用下,测得带有相同孔隙率的不同多孔防波板液罐内的波高具有较高的相似性,并且发现交错排列的多孔结构可以对晃动液体产生较大的阻尼力。Ren等[28]对正弦激励下带有弹性板的矩形罐内的液体晃动进行了研究,结果表明,与自由液面等高的弹性板在变形时会引起液体飞溅,飞溅的液体可以通过对空气的捕捉耗散罐内波浪的能量。除隔板、防波板和柔性板外,Wang等[29]研究了弹性膜在刹车激励作用下对罐内液体晃动的影响,结果表明,弹性膜对晃动引起的纵向力和横向力矩具有很好的抑制作用,显著降低了液体晃动的幅度,并且由于膜的存在,罐内液体不会出现较强的水波和飞溅液体。
综上可知,目前关于防波板的研究大多只针对固定充液比下防波板的数量和防波板的放置位置对液体晃动的影响,鲜有研究一定开孔面积和不同充液高度下防波板的开孔位置和开孔数量对液体晃动的影响,而且上述研究未对防波板的开孔面积进行限制,但是国家标准[30]对液罐车防波板开孔面积有明确的规定。基于此,本文中,首先建立液体晃动的动力学模型,并通过实验验证该模型的有效性;利用验证的数值模型对具有20%固定开孔面积的多孔防波板进行研究,详细分析多种充液高度下防波板的开孔数量和开孔位置对罐内液体晃动的影响。
1. 数值模拟方法与实验准确性检验
1.1 数值模拟方法
有限体积法是计算流体力学领域较成熟的算法,具有对网格适应性较强、稳定性较好以及求解过程可以开启并行计算缩短求解时间的优点,实验中采用内置有限体积法和流体体积法求解器的开源软件OpenFOAM进行数值模拟研究。求解器中控制方程为N-S方程(Navier-Stokes equations)和连续性方程,分别表示为:
∂ρui∂t+∂ρuiuj∂xj=−∂p∂xi+∂∂xj[μ(∂ui∂xj+∂uj∂xi)]+fi (1) ∂ρ∂t+∂ρui∂xi=0 (2) 式中:u为流体的速度,ρ为流体的密度,p为流体压力,μ为动力黏度,fi为作用在液体上的体积力,t为时间,x为坐标,下标i和j代表流场的方向。
为准确捕捉罐体内自由液面的变形,数值模型采用了VOF(volume of fluid)法监测自由液面的变化,VOF法追踪自由液面的原理表达式为:
∂H∂t+∇⋅(uH)+∇[urH(1−H)]=0 (3) 式中:H为流体的相分数,u为流体的速度矢量,ur为流体的相对速度。
VOF法中计算两相交界面的混合密度ρ和动力黏度μ的表达式分别为:
ρ=Hρl+(1−H)ρg (4) μ=Hμl+(1−H)μg (5) 式中:μl和ρl分别为液体的动力黏度和密度,μg和ρg分别为气体的动力黏度和密度。
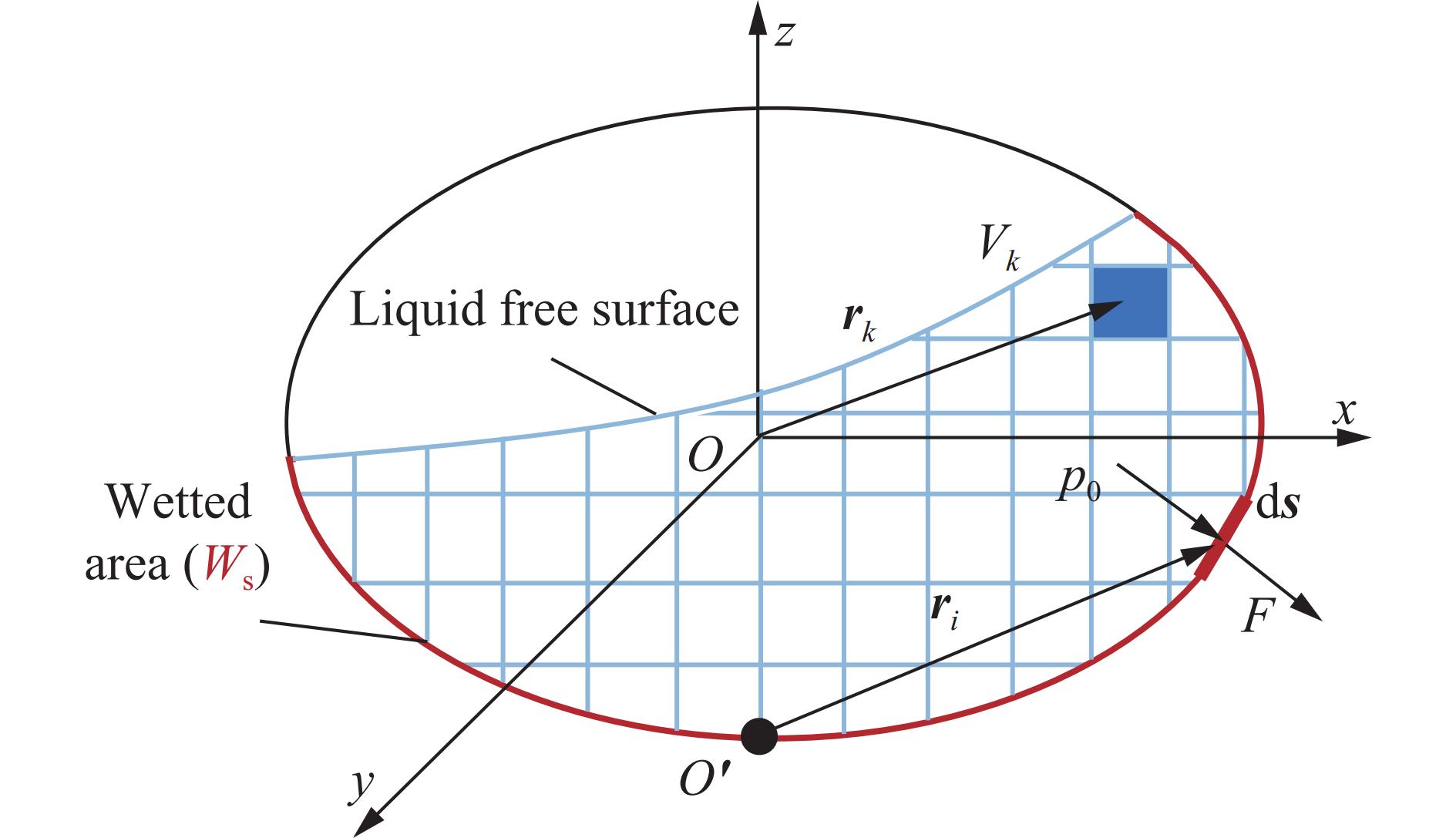
如图1所示,对作用在固-液交界面(湿周)Ws上的压强进行积分,可以求得液体晃动引起的晃动力F:
F=∭p0ds (6) 式中:p0为晃动液体作用在湿周网格上的压强;ds为湿周上网格的面积矢量,方向指向容器壁面外法线方向。
对从参考点O'指向湿周上网格中心处的位置矢量和网格单元上合力的向量积进行积分,可得力矩M:
M=ri×F=∭p0⋅rids (7) 式中:ri为从参考点指向湿周上网格中心的位置矢量。
将容器的充液区域划分为如图1所示的n个网格后,液体质心的空间坐标表示为:
r=1Vn−1∑k=0Vkrk (8) 式中:V为晃动液体的总体积,Vk为第k个网格内液体的体积,rk为从坐标原点指向第k个网格中心的位置矢量。
在数值模拟研究中,罐壁和内部防波板均设置为无厚度且不可变形的壁面,壁面边界设置为无滑移边界条件。无滑移边界条件为:
∂un∂n=0 (9) 式中:un为模型中垂直壁面的速度分量,n为壁面的法线方向。
使用有限体积法进行仿真研究时,需要通过库朗数(C)对网格尺寸和时间步长进行选择:
C=|u|ΔtΔx (10) 式中:|u|为网格内流体速度矢量的模,∆t为时间步长,∆x为网格在速度方向上的距离。
建立数值模型时,计算质量流量(Qm)和体积通量(Q)的表达式为:
Qm=ρ∫udA (11) Q=Qmρ (12) 式中:dA为两相邻网格公共面的面积。
实验中采用了层流模型,并假设流体的运动是无旋的和不可压的。液体晃动数值模型的计算流程如下。
(1) 将t时刻的收敛解(或者初始猜测值)作为t+∆t时刻的初始猜测值,包括速度u、压强p、密度ρ和黏度μ。
(2) 基于式(11)和(12)求解质量流量Qm和体积通量Q。
(3) 基于式(3)更新相分数H。
(4) 基于式(4)和(5)求解密度ρ和动力黏度μ。
(5) 基于式(1)和(2),采用PIMPLE算法求解速度u、压强p和通量场,直至收敛。
(6) 若未超过设定的结束时间,则重复(1)~(5),否则计算结束。
数值模型的具体建立流程如图2所示,图中使用2次判断来表示液体晃动数值模型中的PIMPLE算法和时间步的更新。在第1个判断中,PIMPLE算法会对速度,压强和通量场的收敛性进行判断,若不收敛,则重复步骤(5)的计算,反之完成PIMPLE算法并进入下一步判断。在第2个判断中,需要对当前仿真时间tc是否等于仿真结束时间te进行判断,若tc不等于te,则更新时间步并继续进行下一时间步的仿真,反之结束当前仿真。
1.2 数值模拟方法准确性检验
使用数值模拟方法对车辆制动时液罐内的液体晃动进行研究之前,需要通过实验验证数值模拟方法的有效性。将数值模拟方法获得的液体晃动频率、壁面压强和波高以及仿真得到的自由液面波形与实验进行对比,以验证数值模拟方法的有效性。实验中空气的密度和黏度参数分别设置为1 kg/m3和14.8 mm2/s,水的密度和黏度参数分别设置为1 000 kg/m3和1 mm2/s。
1.2.1 液体晃动频率
研究首先对照Romero等[31]在不同充液比下测得水平放置的直径DR=0.25 m的圆柱形罐体的固有频率。数值实验中,最小网格尺寸设置为5 mm,时间步长设置为0.010 s。对仿真测得的横向力进行快速傅里叶变换(fast Fourier transform,FFT)得到如图3(a)所示的频谱图。将变换后得到的频率与实验和解析结果进行对比(见图3(b)),可以看出,充液比为50%时,对应的仿真测得的频率与实验和解析结果的最大误差分别为4.73%和4.27%,表明仿真实验测得的结果比较可靠。
1.2.2 壁面压强和波高
对比Xue等[32]的三维液体晃动实验测得的压强和波高,对数值模型的准确性进行验证。通过实验对水平余弦激励作用下带有矩形开孔防波板的立方体液罐进行了研究,实验加速度表示为:
¨x=Aω2cos(ωt) (13) 式中:振幅A=0.03 m,角频率ω=6.582 3 rad/s。数值实验中最小网格尺寸为5 mm,时间步长为0.010 s。
该实验测得了壁面P1点处的压力曲线(见图4(a)),从图中可以看到,仿真与实验在P1点的压力曲线基本一致。图4(b)所示的波高曲线中,仿真获得的波高曲线与实验获得的波高曲线基本吻合,较高的重合度证明了数值模拟结果具有较高的可靠性。
1.2.3 自由液面波形
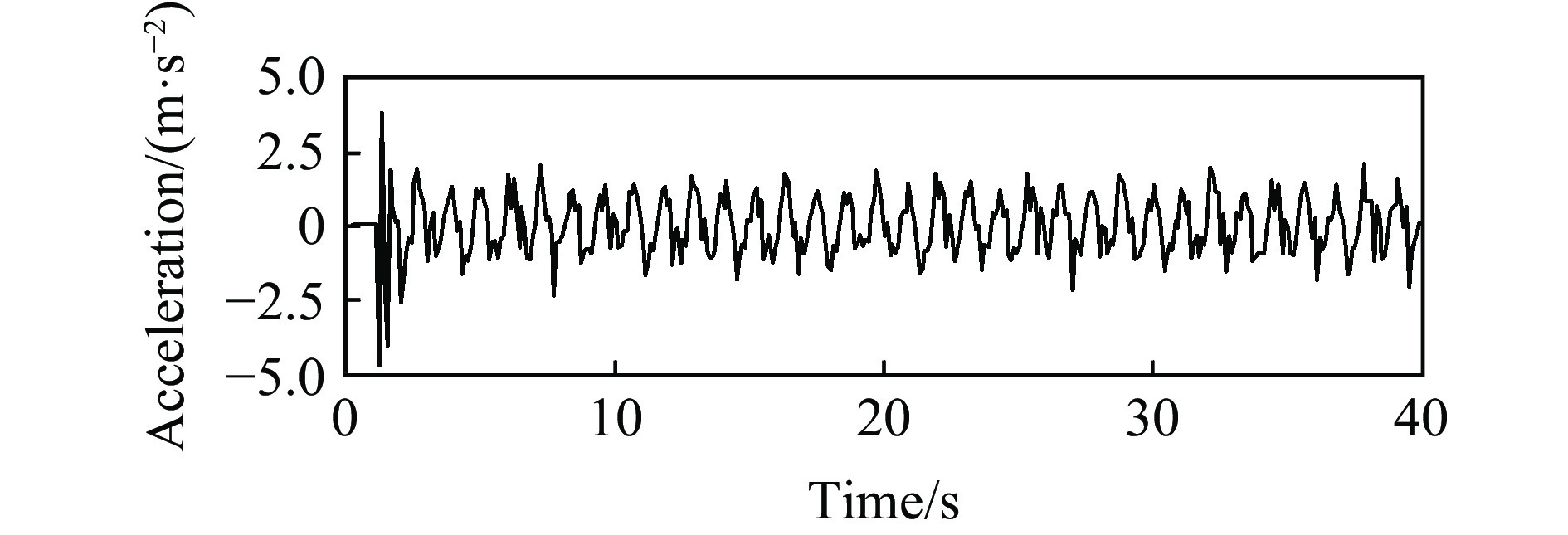
对照实验与数值模拟得到的不同时刻的自由液面图像验证数值模型的准确性。实验中设置了尺寸为300 mm×395 mm×40 mm的矩形液罐,液罐的材质为经特殊处理的有机玻璃,如图5所示。将矩形液罐底部固定在振动台的水平滑块上,通过控制电机的转速对矩形液罐施加不同的外部激励,激励平台的最大水平位移设置为70 mm,实验采用的液体为添加染色剂的水,传感器测得的加速度曲线如图6所示,数值实验中的最小网格尺寸为5 mm,时间步长设置为0.005 s。
相同激励条件下,数值模拟和实验得到的自由液面图像如图7所示。从图7可以看出,仿真图像能准确地捕捉到自由液面的变形及液体撞击罐壁时的爬升过程,与晃动实验得到的自由液面图像吻合程度较高。这表明数值模拟可以准确地反映罐内液体的运动状态,仿真结果具有较高的参考意义。
2. 实验模型和网格无关性检验
2.1 实验模型
实验采用如图8所示的长L=7.55 m、直径D=2.03 m的圆柱形罐体,罐体内部设置3块等间距分布的防波板B1、B2、B3(L1=1.887 5 m)。纵向力为采用式(6)计算所得的合力沿图8中x轴方向的分力。俯仰力矩由式(7)计算得到,式(7)中,位置矢量ri的起点设置在图8所示的罐体截面O处。载荷转移是罐内晃动液体的质心位移,可由式(8)所得的位置矢量r表示。
王琼瑶等[33]在研究中发现,防波板的开孔面积为20%时,其对液体晃动具有较明显的抑制效果,因此,本实验研究了7种横向防波板在20%的开孔面积下,防波板上的开孔数量和孔的分布对液体晃动的影响。如图9所示,将具有不同防波板的罐体命名为T0、T1、T2a、T2b、T3a、T3b、T4a和T4b罐,所有防波板的半径R均为1.015 m。其中T0罐为不添加任何防波板的罐,T1罐内安装了在中心开1个半径r1=0.454 m圆孔的传统防波板。除T1罐内的防波板外,其余防波板上的孔均匀分布在半径r0=0.507 5 m的圆上,T2a-b罐内防波板开有2个半径r2=0.321 m的圆孔,T3a-b罐内防波板开有3个半径r3=0.262 m的圆孔,T4a-b罐内防波板开有4个半径r4=0.227 m的圆孔。
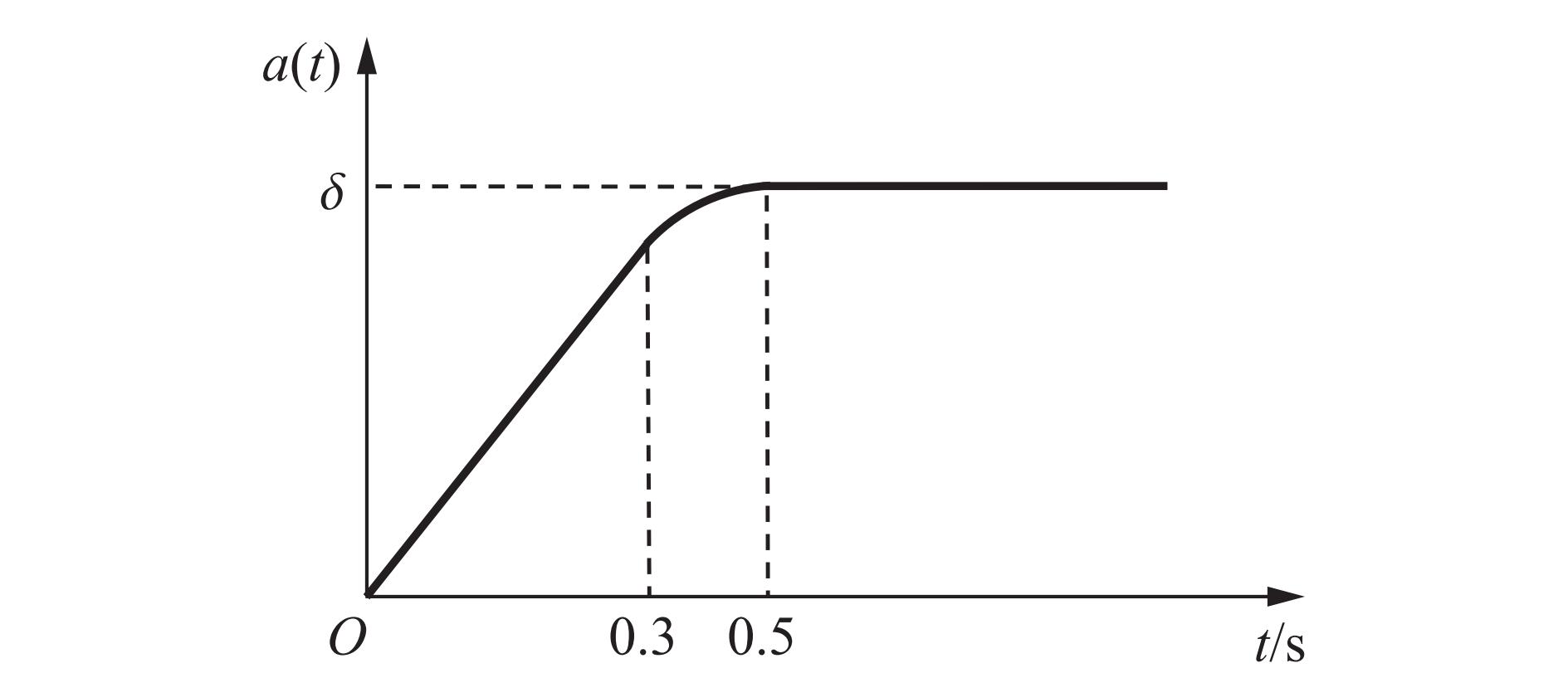
选择如图10所示的加速度曲线来模拟装载柴油的罐车的制动过程。实验中,采用常温下的柴油作为填充介质,其密度为821.25 kg/m3,黏度为5.05 mm2/s。
刹车过程中的加速度变化表示为:
a(t)={αtt≤0.3δ−σ+√σ2−(t−0.5)20.3<t≤0.5δt>0.5 (14) 式中:a(t)为纵向加速度;δ为0.3g加速度时的稳态值;α为加速上升速率,取9.14;加速度上升期到稳定期的过度系数σ的取值为0.2。
2.2 网格无关性检验
数值实验的结果对网格尺寸和时间步长的依赖性非常大,因此在进行数值实验之前需要进行网格尺寸与时间步长的无关性检验。
根据库朗数选用粗网格(最小网格尺寸∆x=6 cm)、中等网格(最小网格尺寸∆x=5 cm)和细网格(最小网格尺寸∆x=4 cm)等3种不同的网格尺寸,在0.005 s的时间步长下进行网格无关性验证。图11为刹车激励下充液比为50%时纵向力的变化曲线。由局部放大图可知:网格尺寸为6和5 cm时对应的曲线具有较高的重合度,为保证数值结果的准确性,选择最小网格尺寸为5 cm的数值模型进行时间步长的选择较合理。
在最小网格尺寸∆x=5 cm的基础上,根据库朗数选择了0.010、0.005和0.002 s 等3种时间步长进行无关性验证。图12显示了不同时间步长下纵向力的变化曲线,观察局部放大图像发现:0.005和0.010 s时间步长对应的纵向力曲线具有较高的重合度。考虑到计算结果的准确性,后续研究选择中等网格尺寸与0.005 s的时间步长较合理。
3. 结果与讨论
实验研究了防波板的开孔数量和开孔位置对罐内液体晃动的影响,根据晃动响应参数(纵向力、俯仰力矩和载荷转移)的峰值和晃动响应参数的下降率评估不同防波板对液体晃动的影响。
3.1 防波板对液体晃动的影响
由于纵向力和俯仰力矩直接影响罐车运行的稳定性,因此,选择纵向力和俯仰力矩对防波板抑制液体晃动的能力进行评估。
图13为充液比为40%、60%和80%时不同罐体内晃动液体产生的纵向力和俯仰力矩的峰值。如图13(a)所示,纵向力峰值随着充液比的增加而增大,带有防波板的罐体内晃动液体的纵向力峰值明显小于相同充液比下T0罐内晃动液体的纵向力峰值,但带有不同防波板的液罐内的纵向力峰值在数值上没有显著差别。这表明在防波板面积一定时,防波板的开孔数量和位置对纵向力的影响并不明显。图13(b)显示了不同充液比下防波板对俯仰力矩的影响,其中T2a对应的俯仰力矩峰值在所有带防波板的液罐中最大,而T2b对应的俯仰力矩峰值在所有带防波板的液罐中最小,表明T2b防波板可以有效地抑制俯仰力矩的峰值,同时也说明开孔位置对俯仰力矩的峰值有较大的影响。
为具体了解T2b防波板对液体晃动的影响,以T0和T2b罐在充液比为60%时晃动响应参数的变化为例。从图14(a)~(b)看出,防波板对罐内纵向力和俯仰力矩峰值的抑制非常明显,并且罐内液体晃动的持续时间也大大缩短。由于液体晃动导致的载荷转移会影响液罐车的行驶安全[9],所以对T2b罐内液体的载荷转移进行研究是有必要的。从图14(c)~(d)可以看出,T2b防波板会大幅降低晃动液体在纵向和竖直方向的转移距离以及晃动液体达到稳定状态的时间。
T1和T2b防波板的开孔数量和开孔位置都存在区别,为评估2种防波板的性能差距,将T1和T2b罐内晃动响应参数的峰值相对于T0罐内晃动响应参数峰值的下降率进行了统计,如表1所示。结果表明:T2b罐晃动响应参数的下降率基本都大于T1罐的下降率,并且随着充液比的增加,T1罐和T2b罐对应的俯仰力矩和载荷转移的下降率呈现出先下降后上升的趋势。
表 1 T1和T2b晃动响应参数峰值相对于T0罐的下降率Table 1. Decrease rate of the peak sloshing response parameters of T1 and T2b relative to T0 tank充液比/% T1相对于T0的下降率/% T2b相对于T0的下降率/% 纵向力 俯仰力矩 载荷转移 纵向力 俯仰力矩 载荷转移 40 27.8 23.6 26.6 29.6 31.9 34.4 60 29.3 21.9 19.4 29.7 29.6 28.8 80 30.0 38.0 45.4 32.4 53.4 68.2 3.2 充液高度对液体晃动的影响
为研究防波板对液体晃动的影响,对T1和T2b液罐进行了不同充液高度的晃动实验,选择自由液面分别过防波板上孔的上、下顶点和圆心3种液面高度,结果如图15所示。充液高度为1.015 m时,2种防波板对液体晃动的抑制效果均较差。这可能是因为充液高度靠近防波板的开孔位置时,晃动液体可以更容易通过圆孔进行纵向转移,造成防波板对液体晃动的抑制能力下降。
为进一步研究充液高度与下降率之间的关系,通过观察现有数据,决定以充液高度0.715 m处为起点,考虑到网格尺寸对计算精度的影响,以0.100 m为增量,进行7组对照实验。表2显示了不同充液高度下T1罐和T2b罐的晃动响应参数,随着充液高度的增加,纵向力和载荷转移峰值分别呈上升和下降趋势,而俯仰力矩峰值则先上升后下降,充液高度为1.115 m时T1罐和T2b罐的俯仰力矩峰值同时取得最大值。
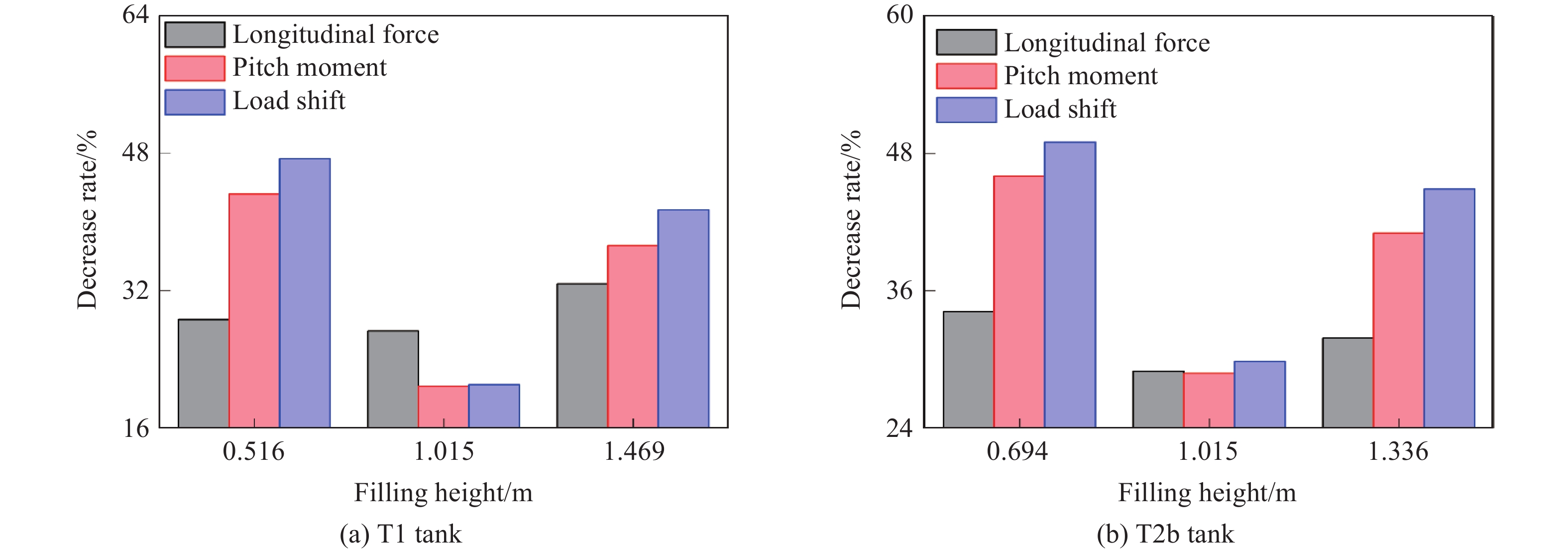
表 2 T1和T2b罐晃动响应参数峰值Table 2. Peak values of sloshing response parameters of T1 and T2b tanks充液高度/m T1罐晃动响应参数峰值 T2b罐晃动响应参数峰值 纵向力/kN 俯仰力矩/(kN·m) 载荷转移/m 纵向力/kN 俯仰力矩/(kN·m) 载荷转移/m 0.715 23.7 105.8 1.56 23.4 88.1 1.26 0.815 28.6 130.6 1.58 27.7 112.5 1.35 0.915 32.9 147.0 1.50 33.0 133.8 1.35 1.015 38.5 153.6 1.34 37.6 138.2 1.19 1.115 42.7 155.7 1.18 42.2 142.3 1.06 1.215 46.7 149.1 0.97 45.9 130.1 0.82 1.315 50.4 135.8 0.75 48.3 113.6 0.60 图16评估了不同充液高度下防波板的表现,发现随着充液高度增加,T2b罐和T1罐内晃动响应参数峰值的下降率基本满足先下降后增高的规律。这是因为在较低的充液高度下,防波板的未开孔部分可以有效抑制液体的纵向晃动。随着充液高度的增加,罐内晃动液体可以通过防波板上的圆孔纵向转移,导致防波板对液体晃动的抑制效果减弱。在较高的充液情况下,受液体晃动的影响,隔间内较易形成密闭空间并引起隔间内气压上升,隔间内升高的气压可以有效抑制罐内液体的纵向晃动[33]。
对比表2与图16发现,T2b罐内俯仰力矩峰值出现时,罐内晃动响应参数的下降率取得最小值,而T1罐俯仰力矩出现时,晃动响应参数下降率的最小值并未同时出现。考虑T1和T2b罐的不同表现,选择对T1罐晃动响应参数下降率取得最小值是对应的充液高度取平均值后进行晃动实验。结果表明:充液高度为1.065 m时,T1罐内的俯仰力矩峰值为155.8 kN∙m,T1罐的3种晃动响应参数的峰值下降率分别为25.81%(纵向力)、20.42%(俯仰力矩)和19.75%(载荷转移),低于图16中1.015和1.115 m对应的下降率。通过研究自由液面高度对液体晃动的影响,发现T1和T2b罐内俯仰力矩峰值出现时对应的液高位置不同,当俯仰力矩峰值出现时,防波板对液体晃动的抑制能力最差。这是因为当充液高度接近防波板上的圆孔时,罐内晃动液体更容易通过圆孔进行纵向转移,造成防波板对晃动响应参数峰值的抑制能力下降,导致晃动响应参数峰值的下降率减小。
为观察T1和T2b防波板对液体晃动的影响,图17显示了充液比为50%时T1罐和T2b罐内自由液面在t=2.9 s时的变形,发现在T1罐最右端舱室内形成了较强的行波并冲击罐顶,并且T1罐最右端隔间内的液体明显多于T2b罐,这是T1罐内晃动响应参数峰值较大的原因。
4. 结 论
在刹车激励作用下,罐体内会出现液体晃动现象,为了削弱液体晃动现象带来的不利影响,使用固定开孔面积为20%的全尺寸防波板进行研究,得到以下主要结论。
(1) 在20%的固定开孔面积下,防波板的开孔位置和开孔数量对纵向力峰值的影响不大。
(2) 在20%的固定开孔面积下,防波板的开孔位置对俯仰力矩峰值的影响较明显。低充液比下,开孔位置越低,俯仰力矩峰值越小;充液比大于60%时,开孔位置越高,俯仰力矩峰值越大。
(3) 开孔防波板不仅可以有效抑制罐内晃动响应参数的峰值,还可以明显缩短罐内晃动液体达到稳定的时间。
(4) 对于长7.55 m、直径2.03 m的圆柱形罐体,其内部等间距分布的3块防波板上分别开2个半径为0.321 m的圆孔,且圆孔水平分布在半径为0.507 5 m的圆上时,防波板对罐内液体晃动的抑制最有效。
-
表 1 T1和T2b晃动响应参数峰值相对于T0罐的下降率
Table 1. Decrease rate of the peak sloshing response parameters of T1 and T2b relative to T0 tank
充液比/% T1相对于T0的下降率/% T2b相对于T0的下降率/% 纵向力 俯仰力矩 载荷转移 纵向力 俯仰力矩 载荷转移 40 27.8 23.6 26.6 29.6 31.9 34.4 60 29.3 21.9 19.4 29.7 29.6 28.8 80 30.0 38.0 45.4 32.4 53.4 68.2 表 2 T1和T2b罐晃动响应参数峰值
Table 2. Peak values of sloshing response parameters of T1 and T2b tanks
充液高度/m T1罐晃动响应参数峰值 T2b罐晃动响应参数峰值 纵向力/kN 俯仰力矩/(kN·m) 载荷转移/m 纵向力/kN 俯仰力矩/(kN·m) 载荷转移/m 0.715 23.7 105.8 1.56 23.4 88.1 1.26 0.815 28.6 130.6 1.58 27.7 112.5 1.35 0.915 32.9 147.0 1.50 33.0 133.8 1.35 1.015 38.5 153.6 1.34 37.6 138.2 1.19 1.115 42.7 155.7 1.18 42.2 142.3 1.06 1.215 46.7 149.1 0.97 45.9 130.1 0.82 1.315 50.4 135.8 0.75 48.3 113.6 0.60 -
[1] JIANG Z, SHI Z, JIANG H, et al. Investigation of the load and flow characteristics of variable mass forced sloshing [J]. Physics of Fluids, 2023, 35(3): 033325. DOI: 10.1063/5.0142148. [2] KIM S P, CHUNG S M, SHIN W J, et al. Experimental study on sloshing reduction effects of baffles linked to a spring system [J]. Ocean Engineering, 2018, 170: 136–147. DOI: 10.1016/j.oceaneng.2018.10.001. [3] MARTINEZ-CARRASCAL J, GONZALEZ L M. On the experimental scaling and power dissipation of violent sloshing flows [J]. Journal of Fluids and Structures, 2022, 115: 103763. DOI: 10.1016/j.jfluidstructs.2022.103763. [4] 刘汉武, 张华, 胡震宇, 等. 基于SPH方法航天器含贮箱液体晃动分离动力学研究 [J]. 中国科学: 技术科学, 2021, 51(8): 938–947. DOI: 10.1360/SST-2021-0123.LIU H W, ZHANG H, HU Z Y, et al. Simulation analysis of liquid sloshing separation in spacecraft with tank based on SPH method [J]. Scientia Sinica Technologica, 2021, 51(8): 938–947. DOI: 10.1360/SST-2021-0123. [5] 林晓冬, 张锐, 刘芳, 等. 基于变分模态分解的复杂航天器姿态扰动分析 [J]. 振动与冲击, 2023, 42(13): 303–309. DOI: 10.13465/j.cnki.jvs.2023.13.036.LIN X D, ZHANG R, LIU F, et al. Attitude disturbance analysis for complex spacecraft based on variational mode decomposition [J]. Journal of Virbation and Shock, 2023, 42(13): 303–309. DOI: 10.13465/j.cnki.jvs.2023.13.036. [6] LI X S, REN Y Y, ZHENG X L, et al. Model-free adaptive control for tank truck rollover stabilization [J]. Mathematical Problems in Engineering, 2021, 2021: 1–16. DOI: 10.1155/2021/8417071. [7] 杨秀建, 吴相稷, 邢云祥, 等. 非满载液罐半挂汽车列车侧向耦合动力学模型 [J]. 中国公路学报, 2018, 31(11): 244–254. DOI: 10.3969/j.issn.1001-7372.2018.11.026.YANG X J, WU X J, XING Y X, et al. Lateral dynamics modeling for partly filled tractor sem-trailer tank vehicle [J]. China Journal of Highway and Transport, 2018, 31(11): 244–254. DOI: 10.3969/j.issn.1001-7372.2018.11.026. [8] 包文红, 张应龙, 班涛, 等. 液罐车内液体晃动对防波板的冲击仿真 [J]. 油气储运, 2022, 41(9): 1087–1094. DOI: 10.6047/j.issn.1000-8241.2022.09.012.BAO W H, ZHANG Y L, BAN T, et al. Simulation on impact of liquid sloshing on baffles in liquid tankers [J]. Oil & Gas Storage and Transportation, 2022, 41(9): 1087–1094. DOI: 10.6047/j.issn.1000-8241.2022.09.012. [9] IRANITALAB A, KHATTAK A, BAHOUTH G. Statistical modeling of cargo tank truck crashes: rollover and release of hazardous materials [J]. Journal of Safety Research, 2020, 74: 71–79. DOI: 10.1016/j.jsr.2020.04.010. [10] CAVALAGLI N, BISCARINI C, FACCI A L, et al. Experimental and numerical analysis of energy dissipation in a sloshing absorber [J]. Journal of Fluids and Structures, 2017, 68: 466–481. DOI: 10.1016/j.jfluidstructs.2016.11.020. [11] POGULURI S K, CHO I H. Liquid sloshing in a rectangular tank with vertical slotted porous screen: based on analytical, numerical, and experimental approach [J]. Ocean Engineering, 2019, 189: 106373. DOI: 10.1016/j.oceaneng.2019.106373. [12] FAN X S, HU Z H, ZHENG X. Research on influence of tank sloshing on ship motion response under different wavelengths [J]. Applied Sciences, 2022, 12(17): 8647. DOI: 10.3390/app12178647. [13] YE W B, LIU J, LIN G, et al. High performance analysis of lateral sloshing response in vertical cylinders with dual circular or arc-shaped porous structures [J]. Applied Ocean Research, 2018, 81: 47–71. DOI: 10.1016/j.apor.2018.09.017. [14] SHAO J R, LI S M, LI Z R, et al. A comparative study of different baffles on mitigating liquid sloshing in a rectangular tank due to a horizontal excitation [J]. Engineering Computations, 2015, 32(4): 1172–1190. DOI: 10.1108/ec-12-2014-0251. [15] BAI W, LIU X, KOH C G. Numerical study of violent LNG sloshing induced by realistic ship motions using level set method [J]. Ocean Engineering, 2015, 97: 100–113. DOI: 10.1016/j.oceaneng.2015.01.010. [16] WEN X, ZHAO W W, WAN D C. Multi-phase moving particle semi-implicit method for violent sloshing flows [J]. European Journal of Mechanics-B/Fluids, 2022, 95: 1–22. DOI: 10.1016/j.euromechflu.2022.04.002. [17] ZHANG A M, LI S M, CUI P, et al. A unified theory for bubble dynamics [J]. Physics of Fluids, 2023, 35(3): 033323. DOI: 10.1063/5.0145415. [18] LI S M, ZHANG A M, CUI P, et al. Vertically neutral collapse of a pulsating bubble at the corner of a free surface and a rigid wall [J]. Journal of Fluid Mechanics, 2023, 962: A28. DOI: 10.1017/jfm.2023.292. [19] MA C L, XIONG C W, MA G W. Numerical study on suppressing violent transient sloshing with single and double vertical baffles [J]. Ocean Engineering, 2021, 223: 108557. DOI: 10.1016/j.oceaneng.2020.108557. [20] RAKHEJA S, SANKAR S, RANGANATHAN R. Roll plane analysis of articulated tank vehicles during steady turning [J]. Vehicle System Dynamics, 1988, 17(1/2): 81–104. DOI: 10.1080/00423118808968896. [21] FANG Q, SUN J, QIU H X, et al. Experimental investigation of liquid sloshing in cylindrical tank with ring baffles under seismic excitation [J]. Arabian Journal for Science and Engineering, 2022, 48(4): 4785–4794. DOI: 10.1007/s13369-022-07182-w. [22] WANG Q Y, LIN G M, JIANG L, et al. Numerical and experimental study of anti-slosh performance of combined baffles in partially filled tank vehicles [J]. International Journal of Pressure Vessels and Piping, 2022, 196: 104555. DOI: 10.1016/j.ijpvp.2021.104555. [23] XUE M A, ZHENG J, LIN P, et al. Violent transient sloshing-wave interaction with a baffle in a three-dimensional numerical tank [J]. Journal of Ocean University of China, 2017, 16(4): 661–673. DOI: 10.1007/s11802-017-3383-8. [24] 曾宪君, 黄志涛, 邵家儒, 等. 基于SPH方法的罐式贮箱动力响应及稳定性研究 [J]. 机床与液压, 2021, 49(14): 24–30, 59. DOI: 10.3969/j.issn.1001-3881.2021.14.005.ZENG X J, HUANG Z T, SHAO J R, et al. Dynamic response and stability analysis of storage tank based on SPH method [J]. Machine Tool & Hydraulics, 2021, 49(14): 24–30, 59. DOI: 10.3969/j.issn.1001-3881.2021.14.005. [25] JIN X, LIU M, ZHANG F, et al. Mitigation of liquid sloshing by multiple layers of dual horizontal baffles with equal/unequal baffle widths [J]. Ocean Engineering, 2022, 263: 112184. DOI: 10.1016/j.oceaneng.2022.112184. [26] ZHANG E H, ZHU W Y, WANG L H. Influencing analysis of different baffle factors on oil liquid sloshing in automobile fuel tank [J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2020, 234(13): 3180–3193. DOI: 10.1177/0954407020919584. [27] TSAO W H, HUANG L H, HWANG W S. An equivalent mechanical model with nonlinear damping for sloshing rectangular tank with porous media [J]. Ocean Engineering, 2021, 242: 110145. DOI: 10.1016/j.oceaneng.2021.110145. [28] REN Y, KHAYYER A, LIN P, et al. Numerical modeling of sloshing flow interaction with an elastic baffle using SPHinXsys [J]. Ocean Engineering, 2023, 267: 113110. DOI: 10.1016/j.oceaneng.2022.113110. [29] WANG Q Y, JIANG L, CHAI M, et al. Numerical and experimental analysis of the effect of elastic membrane on liquid sloshing in partially filled tank vehicles [J]. Mechanics Based Design of Structures and Machines, 2021, 51(3): 1741–1757. DOI: 10.1080/15397734.2021.1875844. [30] 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 液化气体汽车罐车: GB/T 19905—2017 [S]. 北京: 中国标准出版社, 2017. [31] ROMERO J A, HILDEBRAND R, MARTINEZ M, et al. Natural sloshing frequencies of liquid cargo in road tankers [J]. International Journal of Heavy Vehicle Systems, 2005, 12(2): 121–138. DOI: 10.1504/IJHVS.2005.006379. [32] XUE M A, ZHENG J, LIN P. Numerical simulation of sloshing phenomena in cubic tank with multiple baffles [J]. Journal of Applied Mathematics, 2012, 2012: 1–21. DOI: 10.1155/2012/245702. [33] 王琼瑶, 蒋开洪, RAKHEJA S, 等. 部分充液罐车内液体晃动的瞬态响应分析 [J]. 振动与冲击, 2018, 37(17): 1–8. DOI: 10.13465/j.cnki.jvs.2018.17.001.WANG Q Y, JIANG K H, RAKHEJA S, et al. Transient response analysis of liquid slosh in a liquid-partially filled tank truck [J]. Journal of Vibration and Shock, 2018, 37(17): 1–8. DOI: 10.13465/j.cnki.jvs.2018.17.001. 期刊类型引用(3)
1. 张晓军,张银,王有利,汤振齐. 基于流固耦合法的运输罐车不同制动激励下液体晃动研究. 专用汽车. 2025(02): 23-29 .  百度学术
百度学术2. 郭佩杰,陈雨,陈宇翔,汪海英,肖爱萍,陈军,钟培林. 液态粪肥施肥机肥罐防浪板的设计与试验. 农业工程学报. 2025(02): 47-57 .  百度学术
百度学术3. 张杰,罗雪鹏,曾云. 车载液氢储罐运输晃动行为及防晃结构设计. 中国安全科学学报. 2024(11): 81-88 .  百度学术
百度学术其他类型引用(3)
-













 下载:
下载:



























 下载:
下载:















 百度学术
百度学术















