Numerical research on fragment impact damage of typical aircraft structures based on an adaptive FEM-SPH coupling algorithm
-
摘要: 针对飞机典型部位在遭到高速破片攻击后结构整体的战伤状态及破片的剩余行为开展数值模拟。应用LS-DYNA软件，结合有限单元方法（finite element method, FEM）和光滑粒子流体动力学（smoothed particle hydrodynamics, SPH）两者的优势，建立自适应的FEM-SPH耦合模拟方法，并构建2种飞机典型部位的计算模型，采用六面体网格局部细化方法实现了核心位置的精确模拟，并进行试验来验证数值模型；开展了一系列高速冲击战伤模拟，对比了不同工况下破片高速冲击结构后形成的碎片云和破口形貌，并对破片的剩余速度和质量进行分析，确定了破片在结构蒙皮上的临界跳飞角。结果表明：自适应FEM-SPH耦合算法的计算结果与试验结果吻合良好，能够对破片高速冲击战伤进行有效准确模拟；碎片云分布形状随破片速度增加变得狭长，冲击角度会改变碎片云和结构破口形状朝向；碎片云高度和扩散速度随破片速度或角度的变化趋势基本一致并都呈线性关系；破片的速度减少量不随初始速度变化，质量减少量则与冲击速度正相关，两者与冲击角度都负相关；破片临界跳飞角与冲击速度大小基本呈线性关系。
-
关键词:
- 自适应FEM-SPH耦合算法 /
- 高速冲击 /
- 碎片云 /
- 破片冲击
Abstract: A numerical simulation study is carried out on the overall battle damage circumstances of structures and the residual behavior of fragments after the typical parts of aircraft are attacked by high-velocity fragments. An adaptive FEM-SPH coupling simulation method is established by using the LS-DYNA software and combining the advantages of finite element method (FEM) and smoothed particle hydrodynamics (SPH). Using this coupling simulation method, the computational model of two typical parts of the aircraft is set up, and the accurate simulation of the core position is realized by a local refinement method of hexahedral FEM grids. Experiments were carried out to verify the numerical model. A series of high-velocity impact (HVI) battle damage simulations are carried out. The debris cloud and crater appearance formed after fragment impacting on structure at high velocity under different working conditions are compared, while the residual velocity and mass of the fragment are analyzed. The critical ricochet angles of the fragment on the skin are also determined. The major conclusions are given below. The calculation results of the adaptive FEM-SPH coupling algorithm are in good agreement with the experimental results, and it can simulate fragment HVI damage effectively and precisely. The distribution shape of debris cloud becomes narrow and long with the increase of fragment incident velocity, and the incidence angle can change the shape orientation of debris cloud and crater on the structure. The variation trends of height and spread velocity of debris cloud with incident velocity or angle are basically consistent and linear. The velocity reduction of the fragment does not change with the incident velocity, and the mass reduction is positively correlated with it, both of which are negatively correlated with the incidence angle. The critical ricochet angle of fragment varies almost linearly with the incident velocity. The research results can provide a reference for the damage prediction and rapid maintenance of aircraft after air combat. -
在空战中，飞机不仅面临着机载枪炮与导弹的威胁，还要应对这些战斗部爆炸后产生的大量高速破片，飞机在这些高速杀伤元攻击下战伤后的生存力关乎飞行员的生命和空战的结果。在研究有关战伤数据后可以发现，机翼被击中后多数仍可以安全返航，而发动机和油箱中弹后会直接引起机械故障甚至爆炸，严重的会导致机毁人亡。因此，在发动机和油箱这两处典型部位遭受战伤后，其蒙皮破损情况与炮弹破片剩余行为对飞机能否继续安全服役有着至关重要的影响。
一些学者依托试验技术对这些敏感部位的损伤作出了一些分析[1-2]，而受限于高速入射物对气炮能量级和摄像设备灵敏度的高要求，低成本且可重复的数值模拟技术成为了对其进行多工况规模性研究的合适手段。目前，结构遭到高速冲击后的损伤模拟与入射物剩余行为分析相关数值研究多基于有限单元类方法。Jin等[3]建立了双轴经编复合材料的有限单元法（finite element method, FEM）模型，并对冲击后弹丸的剩余速度和复合材料上的损伤进行了分析。邓云飞等[4]使用FEM方法研究了弹体攻角对撞击过程、弹体动能变化和靶板破口及变形的影响。袁潇洒[5]建立了钛/复合材料层板的FEM靶板模型，并分析了层板厚度和弹丸质量对其抗冲击性能和弹道极限的影响。邓希旻等[6]构建了刚体椭圆弹的正穿甲数值模型，分析得到了弹体的高速穿甲阻力函数及剩余速度曲线。有限单元类方法能够满足分析结构损伤形貌和入射物剩余速度的要求，但其通常无法较好地模拟出碎片云的完整形貌轮廓，而且在材料失效后通常使用的删除单元的手段也会带来质量丢失的问题。考虑到无网格粒子法在计算大变形时的显著优势，也有一些研究者在结构建模时直接使用粒子来更好地模拟结构在冲击后产生的碎片云。杨扬[7]采用FEM和光滑粒子流体动力学（smoothed particle hydrodynamics, SPH）方法分别建模对C/SiC复合材料的高速冲击问题进行研究，分析了冲击后的碎片云团和结构损伤破坏模式。强洪夫等[8]引入了一种基于拟流体模型的SPH方法来模拟弹丸在超高速碰撞薄板后形成的碎片云，并分析了弹坑和碎片云的几何特征。Wu等[9]通过分子动力学（molecular dynamics, MD）和SPH模拟研究了超高速撞击下宏观和微观结果之间碎片特征的差异。Cheng等[10]采用FEM和光滑粒子伽辽金（smoothed particle Galerkin, SPG）方法分别对高强度装甲钢进行建模和穿孔数值模拟对比，讨论了2种方法在模拟目标破坏模式和预测弹丸剩余速度时各自的优势。但是大面积地使用粒子法会降低计算精度，而且存在材料边界识别困难等问题，如何处理高应变率下2种不同算法之间固接界面的接触与耦合也是一个不小的挑战。
本文中利用LS-DYNA软件，基于自适应的FEM-SPH耦合方法建立计算模型，对飞机机身几个典型部位遭受高速冲击后的战伤情况进行数值模拟，并开展试验以验证数值模拟模型的准确性和有效性，分析各典型部位在炮弹破片的不同冲击模式下的破口情况和破片剩余行为，以期为发动机和油箱等飞机典型部位的带蒙皮易损结构的优化设计提供参考。
1. 数值模拟模型建立
1.1 自适应FEM-SPH耦合算法原理与软件实现
自适应FEM-SPH耦合算法最早由Johnson等[11-13]提出并应用在高速冲击问题中，其基本思想是将超过应变阈值的FEM单元转化为SPH粒子并与相邻网格连接。近年来，学者们将这一耦合算法应用在航天防护[14-15]、海冰破碎[16]、采煤工程[17]、特殊材料损伤分析[18]等冲击相关领域，都得到了较好的模拟效果。
如图1所示，自适应FEM-SPH耦合算法的实现原理是：首先，在初始化阶段，以自适应的方式在拉格朗日网格实体单元内自动生成一个或多个SPH粒子，这些粒子具有与当地单元相同的物理属性，但处于被约束的状态。接着，在前期FEM单元进行计算时，这些被约束的粒子附着在单元上并随其变形运动，在每一时间步后都从单元上同步更新其速度、压力、密度等场量；当单元上产生的应力或应变超过所给定的材料失效准则的阈值时，这一单元破坏并被删除，此时释放单元处的SPH粒子，继承单元失效前的物理场信息，以活性粒子的状态在光滑域内搜索其他粒子和单元进行耦合计算。最后，被释放的SPH粒子在相互接触和运动的过程中，由于其只能承受压缩应力并相互排斥[19]，粒子在光滑域内搜索到的其他粒子越来越少，计算域逐渐形成稳定的边界。
本文中采用商业软件LS-DYNA中内置的*DEFINE_ADAPTIVE_SOLID_TO_SPH关键字，来实现这一自适应FEM-SPH耦合算法。在软件中，这一耦合算法的计算结果主要由3个控制参数来调节，分别用来控制单元内生成的粒子数量、是否将粒子与周围单元相耦合计算以及设置粒子与周围单元相耦合计算的起始时间。
1.2 FEM网格局部细化
在工程中实际应用自适应FEM-SPH耦合算法时，通常重点关注的问题域相比起整个模型计算域来说很小，因此更为精细化的网格可以得到更加准确的破口毁伤形貌。但相应地，减小单元尺寸带来的单元数量迅速增加会大幅降低计算效率，所以在建模初期进行有限元网格划分时可以采用FEM六面体网格局部细化技术，对2种不同网格尺寸区域之间的相互连接进行共节点处理，实现计算时的直接传力，在保证效率的同时最大限度提高问题域的求解精度。
六面体网格局部细化方法的基本思路是：从3D密网格一侧（图2(a)中区域①）向3D疏网格一侧（图2(a)中区域②）连接的过程中（以正六面体单元作演示），在第1个过渡层内保持纵向面层数不变（图2(a)中区域③），仅在水平面使用四边形单元进行两侧不对等过渡连接（图2(a)中区域④），这样，在第1次过渡处理后结果面就由正方形变为了扁长型单元（图2(a)中区域⑤）；在第2个过渡层内保持水平面不变，对纵向面进行相同的两侧不对等过渡连接（图2(a)中区域⑥），就完成了最基本的疏密过渡。在拐角（图2(b)中区域⑦）等复杂情况处还需要在这基础上作一些其他处理。理论上来说，此方法可实现任意整数比的疏密六面体网格过渡，并且同样适用于更为简化的2D网格。
1.3 数值模拟设置
1.3.1 数值模拟模型
选取飞机典型部位的金属结构模型进行高速冲击的数值模拟。入射破片为半径4 mm的10钢弹塑性球；被冲击的靶板结构分别为取自某型飞机后机身附近的截面OT-4钛合金结构（模型A）和进气道附近的工字型截面7075铝合金结构（模型B），其最大特征长度为250 mm，板厚为1～2 mm，进行有限元离散后的模型如图3所示。
1.3.2 材料模型与接触设置
数值模拟结构模型中：钢使用的材料本构是双线性弹塑性本构模型；钛合金和铝合金所用的是Johnson-Cook (J-C)本构模型，其采用累积损伤来模拟材料的破坏失效，在材料单元的损伤累积参数值达到1时，材料发生破坏，单元删除并激活当地SPH粒子参与后续计算。此外，由于存在较大的密度和温度变化，机身结构材料采用Grüneisen状态方程来计算单元压力。J-C本构模型中计算材料单元屈服强度与断裂塑性应变以及Grüneisen状态方程的具体表达式见文献[8]。所用钢、钛合金和铝合金的材料模型参数见表1，其中ρ、E和ν分别为材料的密度、弹性模量和泊松比，σy为屈服强度，ET为切线模量，cS、SS、Γ为状态方程参数，所用的J-C本构参数见文献[20-21]。
表 1 材料的本构模型和状态方程参数Table 1. Material parameters of constitutive model and quation of state材料 ρ/(kg·m−3) E/GPa ν σy /GPa ET /GPa cS /(m·s−1) SS Γ 10钢 7850 207.0 0.30 1.05 20 OT-4钛 4550 115.0 0.30 5350 1.340 1.97 7075 铝2810 71.7 0.33 5120 1.028 1.23 在模型的破片与结构之间设置面面侵蚀接触和点面侵蚀接触，以保证在整个由高速侵彻导致的表面材料损失过程中的接触有效，防止非物理穿透，分别由关键字*CONTACT_ERODING_SURFACE/ NODES_TO_SURFACE来实现，摩擦因数设置为0.1；使用绑定接触来简化模拟结构板件之间的铆接关系，达到直接传力的效果；由于结构较为复杂，还设置自接触来防止同一部件的碎片自穿透。采用前述的自适应FEM-SPH耦合算法，以准确地模拟出碎片云分布等战伤效果。
2. 破片高速冲击结构的试验与验证
2.1 试验设置
试验采用二级轻气炮作为发射装置，如图4所示。发射的破片使用与数值模拟模型中尺寸和材料相同的实心钢球，其与弹托粘接在一起组成入射物，见图5(a)；被冲击的靶板结构为与数值模拟模型B同尺寸的7075-T6铝合金工字型铆接结构，见图5(b)，板厚为2 mm，通过夹具斜30°固定在靶箱中，见图5(c)。在试验过程中，采用高速相机来捕捉金属剧烈碰撞时产生的大片爆炸碎屑云的形态分布特征。
2.2 数值模拟模型验证
2.2.1 数值收敛性验证
对数值模拟模型B进行网格收敛性验证，提取不同网格单元尺寸下结构体上的最大von Mises等效应力σmax随时间t的变化见图6。
从图6中可以看出，对于较粗尺寸的网格来说，其应力极值震荡不定、变化不够连续（如图6中①～③处），而较细尺寸的网格上应力极值的变化幅度就会小很多（如图6中④处），说明其网格质量较高、收敛性较好。在这里所选取的单一尺寸网格中，0.5 mm单元尺寸的网格稳定性最好，但实际上其计算的时间成本已非常高；另外可以看到，采用了前述局部细化技术的1.5/0.5 mm混合网格的计算结果与0.5 mm的非常相近，且其能大大减少单元和粒子数，减少计算时间，提高计算效率。后面的数值模拟计算中均采用1.5/0.5 mm这一局部细化的混合尺寸网格，模型A和B两种结构所使用的单元总数分别为61万和35万。入射破片整体尺寸相对较小，选用的单元长度为0.2 mm，离散其所使用的单元总数为5万。
2.2.2 试验对比验证
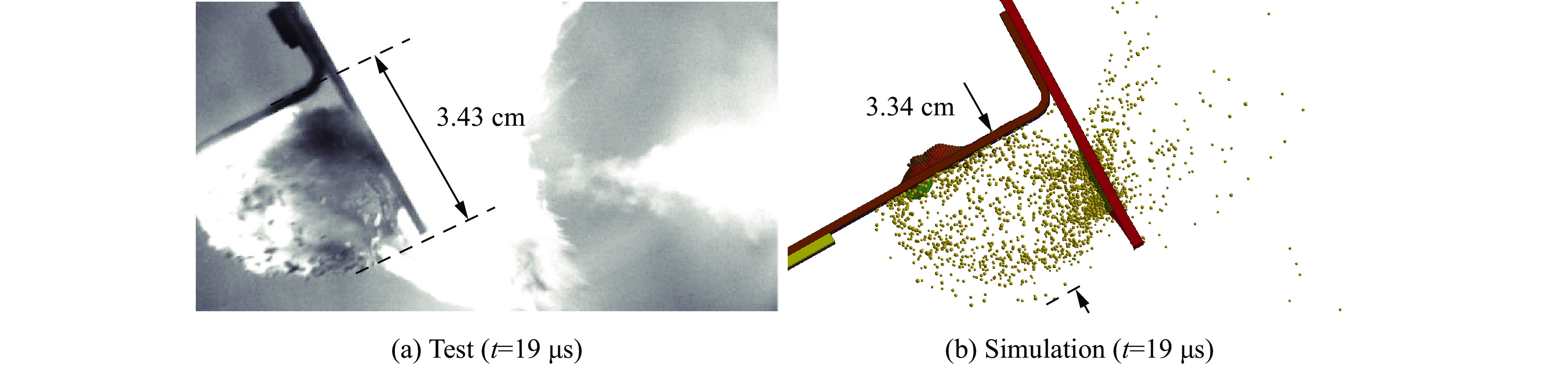
将模型B的数值模拟计算结果与试验所得碎片云进行对比，如图7所示。入射破片的速度均为v0=2.4 km/s，入射方向与外蒙皮法线的夹角为θ0=30°。从对比图可看出，应用了自适应FEM-SPH耦合算法的数值模拟能够很好地模拟出真实的碎片云分布，其宽度尺寸的误差只有3%，这验证了数值模拟方法和模型的有效性，为后续研究分析提供了支撑。
图 7 试验与数值模拟的碎片云分布对比Figure 7. Comparison of debris clouds obtained between test and simulation3. 高速冲击问题数值分析
3.1 结构在高速冲击后的战伤情况
3.1.1 不同入射速度下结果对比
取模型A，破片入射路径为从蒙皮外侧向蒙皮内侧筋条处打击，入射角θ0=30°，并设置以2.6～1.8 km/s、梯度为0.2 km/s递减的不同初始入射速度v0来展开研究。
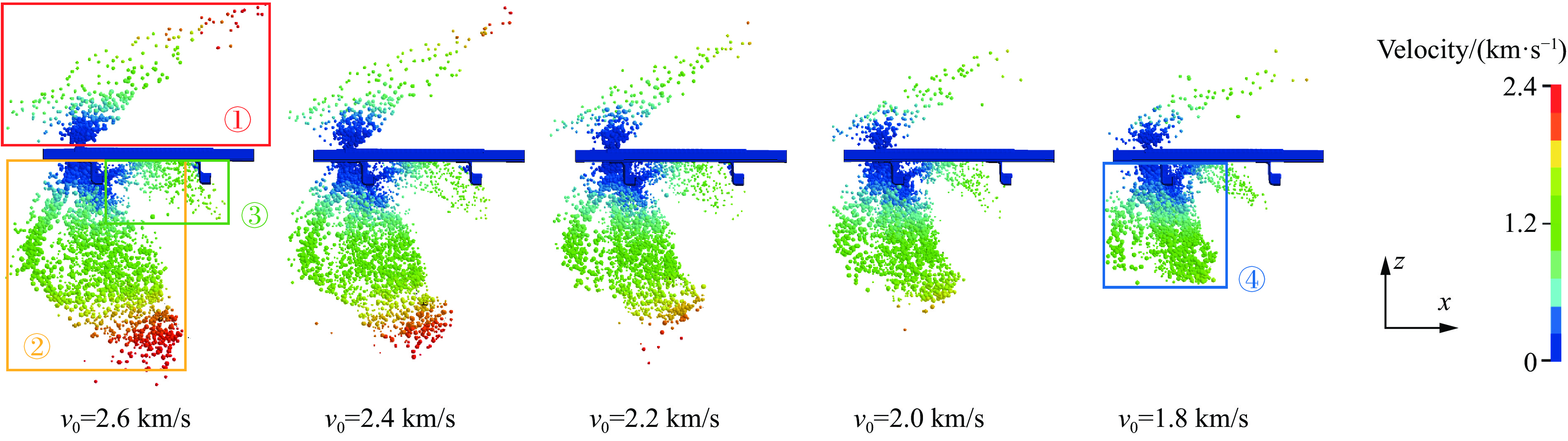
从图8中可看出，在同一时刻（t=100 μs时碎片云扩散状态已稳定，后续云图和碎片云曲线分析均为这一时刻的结果），由于是斜冲击，不同v0下形成的碎片云都大致呈现出直角三角形的分布，蒙皮上方为斜入射溅起的长三角形碎片云（图8中区域①），下方分为两部分，左侧是大量团状碎片粒子（图8中区域②），右上侧为破片冲击到筋条上产生的横向飞溅粒子（图8中区域③）。随着v0的减小，粒子云形状更趋于正三角形（图8中区域④），原因是在高速情况下飞溅粒子在入射轨迹方向获得的分速度比例更大；并且其尺寸也偏小，这是由于同一时刻低速冲击后粒子还未来得及扩散开来。
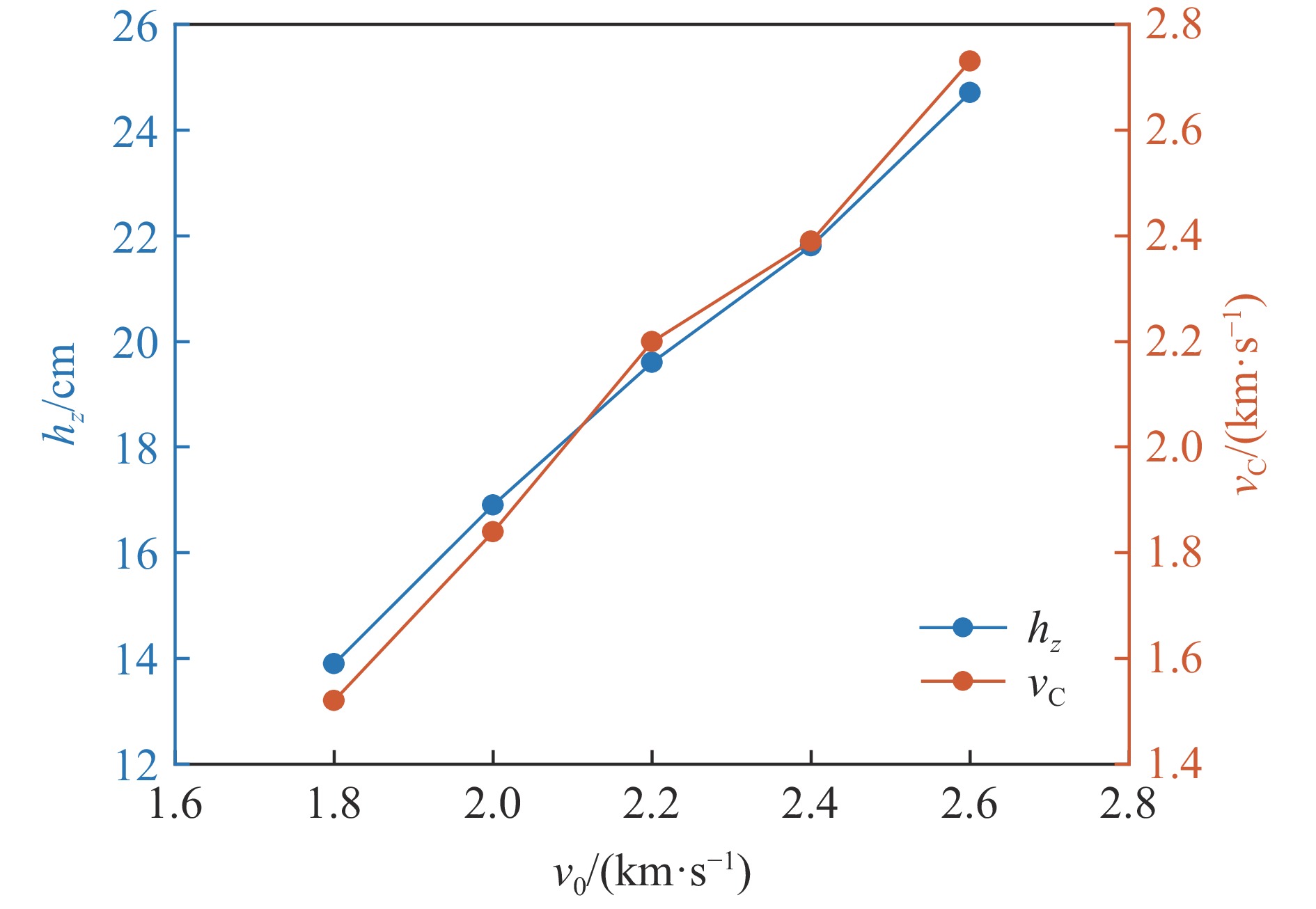
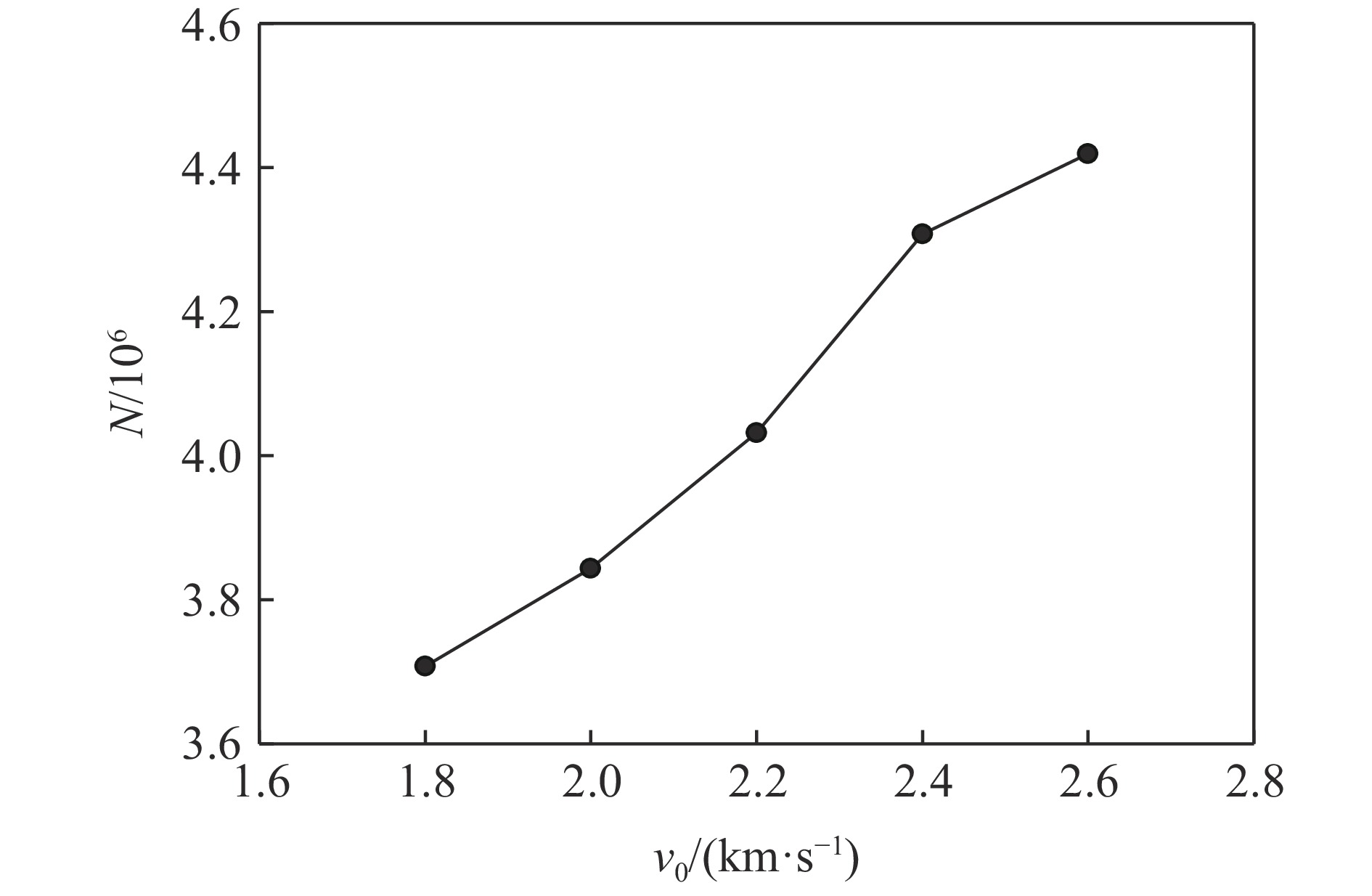
图 8 不同入射速度下的碎片云分布Figure 8. Distributions of debris cloud at different incident velocities图9～10所示为碎片云高度hz、扩散速度vC与其中碎片数量N随初始入射速度v0的变化趋势，其中碎片云高度hz指蒙皮内侧的部分在z方向上的长度，碎片云扩散速度vC指碎片云最外侧粒子的最大速度。可以看到，hz与vC的变化趋势是一致的，3个量基本都与v0呈线性关系。
图 9 不同入射速度下碎片云高度和扩散速度变化曲线Figure 9. Curves of debris cloud height and spread velocity at different incident velocities
图 10 不同入射速度下碎片数量变化曲线Figure 10. Curve of the number of fragments at different incident velocities在高速侵彻过程中，入射破片在与结构摩擦时，动能会转化为热能等其他能量。图11～12给出了不同入射速度v0下破片速度v和质量m随时间t的变化曲线。从图11中可以看出，破片经历了2次速度下降，第1次是在0～8 μs，对应其连续侵彻蒙皮和筋条上缘的过程，速度下降350～400 m/s；第2次是在12～30 μs，对应其连续侵彻筋条中部和下缘的过程，速度同样下降350～400 m/s。值得注意的是，5种情况下v0不同，但经过2次侵彻过程后，速度总减少量基本一致。同样，在高速侵彻过程中，破片的质量也会有所损失，在数值模拟中表现为部分单元失效后转为SPH粒子而导致的有限元部分质量减少。从图12中曲线可以看出，破片经历了2次质量减少，同前述速度变化过程一致，第1次是破片侵彻蒙皮的过程，质量都减少了约1/2；第2次是破片侵彻筋条的过程，其中破片在更高速情况下碰撞摩擦更为剧烈，质量损失量较大，差距较第1次侵彻明显得多。
图 11 不同入射速度下破片速度时间历程曲线Figure 11. Time histories of fragment velocity at different incident velocities
图 12 不同入射速度下破片质量时间历程曲线Figure 12. Time histories of fragment mass at different incident velocities3.1.2 不同入射角度下结果对比
取模型B，破片入射路径为沿中间框平面从斜上到斜下，入射速度为v0=2.4 km/s，并设置竖直平面内从30～80°变化、角度梯度为15°或20°递增的不同初始入射角度θ0来展开研究。
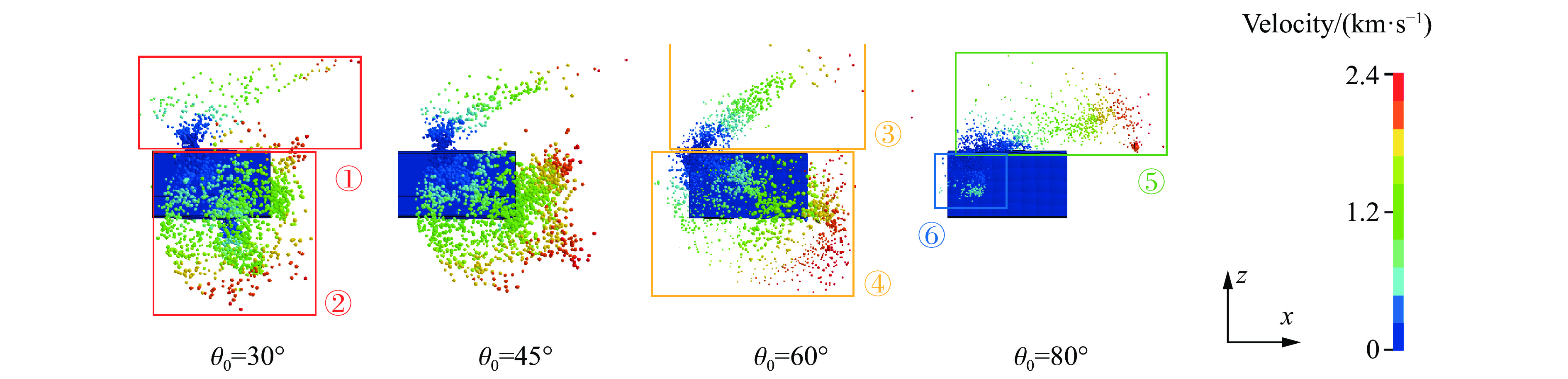
从图13中可以看出，在同一时刻，破片在框上侵彻造成的指状斜破口（图13中区域①～③）也随着θ0的增加而变化，且指尖前方区域由于受到高速挤压而有着较高的应力（图13中区域④～⑥）；到80°入射角时，由于角度过大，破片未能穿透蒙皮并被弹飞，呈现为蒙皮上的一个带裂缝鼓包（图13中区域⑦）。从图14中可以看出，在同一时刻，小入射角情况下，碎片主要集中在入射路径附近（图14中区域①～②）；θ0逐渐增大后，粒子开始变得团状发散（图14中区域③～④）；到了80°的弹飞工况，破片主体未穿透蒙皮，使得粒子碎片云主要分布在外蒙皮板的上方和斜上方（图14中区域⑤），入射点的正下方区域也有少部分剥离带来的小碎片（图14中区域⑥）。
图 14 不同入射角度下的碎片云分布Figure 14. Distributions of debris cloud at different incident angles从图15中可以看出，与前文中类似，碎片云高度hz和扩散速度vC都与破片入射角度θ0基本呈线性关系。图16为不同θ0下碎片数量N与θ0的关系，可以看到，对于复杂结构来说，碎片数量与入射路径是密切相关的。在80°大角度入射情况下，由于破片未穿透蒙皮，仅有少量剥离的碎片粒子，所以其hz与vC值都偏小，碎片数量更是仅有穿透工况的一半。
图 15 不同入射角度下碎片云高度和扩散速度变化曲线Figure 15. Variation of debris cloud height and spread velocity with incident angles
图 16 不同入射角度下碎片数量变化曲线Figure 16. Variation of the number of fragments with incident angles从图17中可以看出，由于速度大小相等，尽管速度方向不同，不同入射角度θ0下入射破片的第1阶段侵彻框导致的速度下降所用的时间差别不大，在第2阶段侵彻内蒙皮的过程中，则表现出了由于θ0不同带来的速度下降量的较大差异，对于80°的弹飞工况更是不存在第2阶段，其速度损失仅有10%。总的来说，随着破片θ0的增加，其速度损失量在逐渐减小。从图18中可以看出，由于与结构体产生了长路径的磨损，前3个工况都经过了多次质量下降的过程，最后的稳定质量都在5%以下，入射破片所剩无几，尤其是45°侵彻的工况中破片剩余质量更是仅有1.6%；80°大角度工况的破片质量下降过程则比较平缓，其质量还剩下1/2。
图 17 不同入射角度下破片速度时间历程曲线Figure 17. Histories of fragment velocity at different incident angles
图 18 不同入射角度下破片质量时间历程曲线Figure 18. Histories of fragment mass at different incident angles3.2 破片临界跳飞角的确定
对于给定的破片入射速度v0，随着初始入射角θ0的逐渐增大，破片在垂直方向（z轴）上的剩余速度vz会降低至零（刚好不穿透），此为穿透阶段；之后进入弹飞阶段，破片在垂直方向上的弹飞速度开始升高，达峰后再降至零。本节中将对确定破片穿透与弹飞的临界跳飞角θc展开研究。
取模型B，在入射破片4组不同入射速度v0下分别计算初始入射角θ0，在vz=0附近选取9个点，使用二次函数vz=aθ02+bθ0+c进行拟合，以确定破片在铝合金制外蒙皮上的临界跳飞角θc，其拟合系数见表2，各速度下拟合曲线的R2均在0.89以上，拟合结果见图19。
表 2 各速度下临界跳飞角拟合曲线的参数Table 2. Parameters of fitting curves to define the critical ricochet angle under different velocitiesv0/(km·s−1) a/(km·s−1) b/(km·s−1) c/(km·s−1) R2 θc/(°) 2.4 −20.2 3001 − 111233 0.9817 72.13 2.2 −7.8 1179 − 44504 0.9497 71.70 2.0 −7.0 1059 − 39745 0.9093 70.69 1.8 −14.3 2105 − 77215 0.8971 70.22 
图 19 各速度下确定临界跳飞角的拟合曲线Figure 19. Fitting curves to define the critical ricochet angle at different velocities将破片的θc与v0关系绘制成曲线，得到图20，可以看出两者基本呈线性变化。
图 20 临界跳飞角与初始入射速度的关系Figure 20. Relation between the critical ricochet angles and initial incident velocities4. 结 论
本文中针对高速破片冲击下飞机典型部位战伤情况展开数值模拟研究，建立一种基于单元失效判定的FEM-SPH自适应转换耦合模拟方法，使用六面体网格局部细化方法建立了计算模型，并对耦合算法和数值模型的有效性和准确性进行试验验证，在此基础上对破片冲击后的战伤情况展开一系列工况的数值模拟，得到的主要结论如下。
(1) 结构的碎片云分布形状随着破片入射速度的降低而变得更为规则，如对于椭圆状的碎片云来说，较低速入射下其偏心率更小；破片入射角度主要影响碎片云的形状朝向，在较大角度入射时由于未穿透蒙皮而导致碎片云只出现在蒙皮一侧。
(2) 初始入射速度不同的情况下，破片的速度降低量基本不变，而剩余质量则随初始入射速度的降低而减小；由于初始入射角度的变化会导致穿过的结构位置不同，速度和质量变化各有不同，但都呈现出入射角越大，剩余速度和质量越小的规律。
(3) 碎片云高度和扩散速度随不同破片入射速度或角度的变化趋势基本一致，其随入射速度增大而增大，随入射角度增大而减小。
(4) 不同的破片初始入射速度下，临界跳飞角与入射速度大小基本呈线性关系。
-
图 7 试验与数值模拟的碎片云分布对比
Figure 7. Comparison of debris clouds obtained between test and simulation
图 8 不同入射速度下的碎片云分布
Figure 8. Distributions of debris cloud at different incident velocities
图 9 不同入射速度下碎片云高度和扩散速度变化曲线
Figure 9. Curves of debris cloud height and spread velocity at different incident velocities
图 10 不同入射速度下碎片数量变化曲线
Figure 10. Curve of the number of fragments at different incident velocities
图 11 不同入射速度下破片速度时间历程曲线
Figure 11. Time histories of fragment velocity at different incident velocities
图 12 不同入射速度下破片质量时间历程曲线
Figure 12. Time histories of fragment mass at different incident velocities
图 14 不同入射角度下的碎片云分布
Figure 14. Distributions of debris cloud at different incident angles
图 15 不同入射角度下碎片云高度和扩散速度变化曲线
Figure 15. Variation of debris cloud height and spread velocity with incident angles
图 16 不同入射角度下碎片数量变化曲线
Figure 16. Variation of the number of fragments with incident angles
图 17 不同入射角度下破片速度时间历程曲线
Figure 17. Histories of fragment velocity at different incident angles
图 18 不同入射角度下破片质量时间历程曲线
Figure 18. Histories of fragment mass at different incident angles
图 19 各速度下确定临界跳飞角的拟合曲线
Figure 19. Fitting curves to define the critical ricochet angle at different velocities
图 20 临界跳飞角与初始入射速度的关系
Figure 20. Relation between the critical ricochet angles and initial incident velocities
表 1 材料的本构模型和状态方程参数
Table 1. Material parameters of constitutive model and quation of state
材料 ρ/(kg·m−3) E/GPa ν σy /GPa ET /GPa cS /(m·s−1) SS Γ 10钢 7850 207.0 0.30 1.05 20 OT-4钛 4550 115.0 0.30 5350 1.340 1.97 7075 铝2810 71.7 0.33 5120 1.028 1.23 
下载: 导出CSV
表 2 各速度下临界跳飞角拟合曲线的参数
Table 2. Parameters of fitting curves to define the critical ricochet angle under different velocities
v0/(km·s−1) a/(km·s−1) b/(km·s−1) c/(km·s−1) R2 θc/(°) 2.4 −20.2 3001 − 111233 0.9817 72.13 2.2 −7.8 1179 − 44504 0.9497 71.70 2.0 −7.0 1059 − 39745 0.9093 70.69 1.8 −14.3 2105 − 77215 0.8971 70.22
下载: 导出CSV
-
[1] 陈远富. 杀伤战斗部作用下典型飞机目标易损性研究[D]. 南京: 南京理工大学, 2016: 49–52. [2] 徐梓熙, 刘彦, 闫俊伯, 等. 不同破片对典型飞机目标的毁伤效应 [J]. 兵工学报, 2020, 41(S2): 63–68. DOI: 10.3969/j.issn.1000-1093.2020.S2.008.XU Z X, LIU Y, YAN J B, et al. Experimental investigation on the damage of aircraft subjected to different fragments loading [J]. Acta Armamantarii, 2020, 41(S2): 63–68. DOI: 10.3969/j.issn.1000-1093.2020.S2.008. [3] JIN L M, HU H , SUN B Z, et al. A simplified microstructure model of bi-axial warp-knitted composite for ballistic impact simulation [J]. Composites Part B: Engineering, 2010, 41(5): 337–353. DOI: 10.1016/j.compositesb.2010.03.006. [4] 邓云飞, 袁家俊. 攻角对卵形头弹撞击铝合金薄板影响的数值研究 [J]. 高压物理学报, 2018, 32(4): 127–133. DOI: 10.11858/gywlxb.20170601.DENG Y F, YUAN J J. Numerical research of influence of attack angle on thin aluminum alloy plate impacted by ogival-nosed projectile [J]. Chinese Journal of High Pressure Physics, 2018, 32(4): 127–133. DOI: 10.11858/gywlxb.20170601. [5] 袁潇洒. TC4/PEEK/Cf层板抗高速冲击性能数值模拟与试验研究[D]. 南京: 南京航空航天大学, 2021: 46–87. [6] 邓希旻, 武海军, 董恒, 等. 椭圆截面截锥弹体的高速穿甲特性及阻力模型 [J]. 爆炸与冲击, 2023, 43(9): 091406. DOI: 10.11883/bzycj-2023-0074.DENG X M, WU H J, DONG H, et al. A study of high-velocity penetration characteristics and resistance model of elliptical cross-section truncated ogive projectile [J]. Explosion and Shock Waves, 2023, 43(9): 091406. DOI: 10.11883/bzycj-2023-0074. [7] 杨扬. C/SiC复合材料抗冲击特性及其数值模拟中的核心算法研究[D]. 西安: 西北工业大学, 2015: 41–68. [8] 强洪夫, 范树佳, 陈福振, 等. 基于拟流体模型的SPH新方法及其在弹丸超高速碰撞薄板中的应用 [J]. 爆炸与冲击, 2017, 37(6): 990–1000. DOI: 10.11883/1001-1455(2017)06-0990-11.QIANG H F, FAN S J, CHEN F Z, et al. A new smoothed particle hydrodynamics method based on the pseudo-fluid model and its application in hypervelocity impact of a projectile on a thin plate [J]. Explosion and Shock Waves, 2017, 37(6): 990–1000. DOI: 10.11883/1001-1455(2017)06-0990-11. [9] WU W D, LIU J M, XIE W, et al. Microscopic and macroscopic fragmentation characteristics under hypervelocity impact based on MD and SPH method [J]. Nanomaterials, 2021, 11(11): 2953. DOI: 10.3390/nano11112953. [10] CHENG Y H, WU H, JIANG P F, et al. Ballistic resistance of high-strength armor steel against ogive-nosed projectile impact [J]. Thin-Walled Structures, 2023, 183: 110350. DOI: 10.1016/j.tws.2022.110350. [11] JOHNSON G R. Linking of Lagrangian particle methods to standard finite element methods for high velocity impact computations [J]. Nuclear Engineering and Design, 1994, 150(2/3): 265–274. DOI: 10.1016/0029-5493(94)90143-0. [12] JOHNSON G R, STRYK R A, BEISSEL S R. An algorithm to automatically convert distorted finite elements into meshless particles during dynamic deformation [J]. International Journal of Impact Engineering, 2002, 27(10): 997–1013. DOI: 10.1016/S0734-743X(02)00030-1. [13] JOHNSON G R, STRYK R A. Conversion of 3D distorted elements into meshless particles during dynamic deformation [J]. International Journal of Impact Engineering, 2003, 28(9): 947–966. DOI: 10.1016/S0734-743X(03)00012-5. [14] HE Q G, CHEN X W, CHEN J F. Finite element-smoothed particle hydrodynamics adaptive method in simulating debris cloud [J]. Acta Astronautica, 2020, 175: 99–117. DOI: 10.1016/j.actaastro.2020.05.056. [15] 杨玉好, 郭香华, 张庆明. 动能块超高速碰撞多层防护结构的毁伤特性数值模拟 [J]. 高压物理学报, 2022, 36(4): 044204. DOI: 10.11858/gywlxb.20220533.YANG Y H, GUO X H, ZHANG Q M. Numerical simulation of damage characteristics of multi-layer protective structure under hypervelocity impact of kinetic energy block [J]. Chinese Journal of High Pressure Physics, 2022, 36(4): 044204. DOI: 10.11858/gywlxb.20220533. [16] CHEN Z, HE Y P, HUANG C, et al. Numerical simulation of sloping structure-level ice interaction based on SPH-FEM conversion algorithm [C]//Proceedings of the 13th International Ocean and Polar Engineering Conference. Shanghai, China: 731–735. [17] 高耀东, 武卫晓. 基于FEM-SPH算法矸石层对采煤机截齿的影响分析 [J]. 煤矿机械, 2020, 41(1): 78–81. DOI: 10.13436/j.mkjx.202001027.GAO Y D, WU W X. Influence analysis of gangue layer on bit of shearer based on FEM-SPH algorithm [J]. Coal Mine Machinery, 2020, 41(1): 78–81. DOI: 10.13436/j.mkjx.202001027. [18] YU S X, FAN Q B, CHENG X W, et al. Numerical simulation of the process of Zr58Nb3Cu12Ni12Al15 bulk glasses fragment penetrating into two separated plates and forming debris cloud [J]. Journal of Materials Research and Technology, 2022, 19: 2115–2125. DOI: 10.1016/j.jmrt.2022.05.142. [19] JOHNSON G R, STRYK R A, GERLACH C A, et al. A quantitative assessment of computational results for behind armor debris [C]//23rd International Symposium on Ballistics. Tarragona, Spain: International Ballistics Society, 2007: 1165–1172. [20] BUZYURKIN A E, GLADKY I L, KRAUS E I. Determination of parameters of the Johnson-Cook model for the description of deformation and fracture of titanium alloys [J]. Journal of Applied Mechanics and Technical Physics, 2015, 56(2): 330–336. DOI: 10.1134/S0021894415020194. [21] BRAR N S, JOSHI V S, HARRIS B W, et al. Constitutive model constants for Al7075-T651 and Al7075-T6 [C]//16th Conference of the American-Physical-Society-Topical-Group on Shock Compression of Condensed Matter. Nashville, TN, US: American Institute of Physics, 2009: 945–948. 期刊类型引用(0)
其他类型引用(1)
-
下载:
计量
- 文章访问数: 126
- HTML全文浏览量: 192
- PDF下载量: 60
- 被引次数: 1