无论是在国防工业还是在民用设施领域，工程结构的抗冲击防护能力都十分重要。金属点阵夹层结构相比于等质量的实体板或梁结构在抗冲击防护方面具有独特的性能优势，主要归因于3个方面：(1) 对于爆炸冲击载荷，由于流固耦合作用，使得传递到夹层结构上的冲量相比于实体结构而言更小，这在水爆中更加明显；(2) 夹层结构具有更大的抗弯刚度；(3) 夹层结构的芯体可以压缩吸能，从而耗散掉载荷带来的部分能量^[1-5]。目前，人们发展了夹层结构多种多样的芯体^[6-8]，其中，金属波纹点阵结构因其制备简单、高比强度、性能稳定等诸多优势^[9-11]而备受研究者青睐，并且得到了广泛的工程应用，尤其是在舰船舱壁结构中^[12-14]。

针对波纹点阵结构的研究开展得很早，1951年，Libove等^[15]就基于Mindlin-Ressiner板理论推导了梯形波纹夹芯板的等效弹性常数。随后，人们针对不同形状波纹及其夹层板结构不同方向的静态弹性参数进行了全面分析^[16-21]，并对结构的动态振动特性开展了相应研究^[21-22]。此外，研究者们对波纹及其夹层结构的屈曲特性、强度特性及大变形吸能能力产生了浓厚兴趣：Nordstrand^[23]分析了波纹夹层结构的后屈曲特性并进行了参数化讨论；Lu等^[24]研究了正弦型波纹结构在准静态面外压缩下的强度及大变形特性，并且讨论了边界条件、几何参数及母材性能的影响；Côté等^[9]将实验、理论与数值仿真相结合，对三角形波纹及菱形棱柱点阵结构的准静态压缩、横纵剪切强度和大变形吸能特性进行了系统分析。同时，波纹夹层结构的三点弯曲强度和大变形行为也被详细研究，并且讨论了波纹取向的影响^[25]。在动态力学性能方面，Tilbrook等^[26]研究了波纹结构和Y型棱柱点阵结构从准静态到200 m/s速度动态撞击下的压溃力学行为，发现这类点阵结构的变形在低速下主要受惯性效应影响，而在高速下受塑性波效应影响较大，其中惯性效应对Y型棱柱点阵结构的影响小于对波纹结构的影响。

在对波纹点阵结构的力学性能有了相对系统的认识后，波纹夹层结构逐渐走向工程应用，而面向工程结构的防护需求，研究者们对波纹芯体夹层结构在各类动态冲击载荷下的力学行为也开展了广泛研究。Hou等^[27]研究了波纹夹层板的准静态压溃性能，在此基础上进一步探究了波纹夹层板在低速局部冲击和平面冲击载荷下的力学性能，发现在所探究的载荷下，三角波纹动态力学性能略优于梯形波纹。Radford等^[10]研究了波纹夹层梁在泡沫子弹冲击下的动态力学性能，发现了其相对于均质板的抗冲击性能优势。Rubino等^[13]进一步探究了波纹夹层梁和Y型芯体夹层梁在泡沫子弹冲击下的响应特点，并且分析了芯体取向的影响，指出沿梁轴向布置芯体的夹层梁的抗冲击性能要优于横向布置芯体的梁结构。研究者们还深入分析了波纹及Y型芯体夹层梁的低速冲击性能^[28]、动态压痕特性^[29]以及夹层板在泡沫子弹冲击下的力学行为^[30]。在实爆载荷方面，研究者们探究了三角形和梯形波纹在球形爆炸波和平面爆炸波作用下结构的变形大小、失效模式等关键指标，并且建立了高精度的仿真模型^[14,31-32]。总体而言，已有研究较为全面地揭示了波纹夹层结构的抗冲击力学特性。

日益复杂严苛的服役环境对工程装备的基础承载及防护性能提出了更高的要求，因此研究者们期望对波纹夹层结构开展强化设计，以进一步增强其静/动态力学性能。常见的设计方法有面板强化^[3,33]、固液耦合^[34]、混杂芯体^[2,35-36]、多级结构^[37-40]等，其中多级结构设计相比其他设计往往不需要引入新的材料体系，并且可以保留波纹结构的通孔特性。对于波纹夹层结构的多级设计，可以从多级芯体^[37]的角度和多级夹层^[38-40]的角度开展。对于大规模工程应用而言，多级芯体的制备存在一定的困难，而多级夹层设计制备工艺更加方便。目前，针对从多级夹层角度设计的多级波纹夹层结构，研究者们深入探讨了其在准静态三点弯曲载荷下的力学性能，发现了其抗弯性能优势^[38-40]。然而，目前仍鲜有研究揭示其动态力学性能，其抗冲击防护能力仍不明晰。因此，本文从多级夹层的角度出发，研究多级波纹夹层梁结构在泡沫子弹冲击下的动态力学行为，与单级波纹夹层结构的抗冲击性能进行对比，比较两者抗冲击性能的优劣，并探究相应的力学机理。

1.   多级金属波纹夹层结构

广义上，如果一个结构由多个层次的子结构组成，且每个层次的子结构具有独立的功能和特征，则这个结构被称为多级结构^[41-42]。自然界中存在许多多级结构的例子。如图1(a)所示，将植物的根茎放大来看，其本身是一个多孔结构；同时，其根茎内外表面由更细小的多孔结构构成，包络着内部较大的多孔结构，从而构成了“多级夹层结构”。人们也开展了一些多级工程结构的设计，如著名的埃菲尔铁塔，如图1(b)所示，其大的桁架结构内部又有小的桁架结构支撑，组成了稳定坚固的整体结构。

图  1  现实中的多级结构^[43-44]

Figure  1.  Hierarchical structures in reality^[43-44]

下载: 全尺寸图片 幻灯片

多级金属波纹结构几何构型如图2所示，其整体由上下板材和内部波纹芯体组成，其中上下板材本身就是单级波纹夹层结构，由波纹芯体和上下面板组成。将整体的波纹夹层结构定义为第一级，构成第一级夹层结构的上下波纹夹层结构板材定义为第二级。结构的几何参数如图中所标注，包括：整体结构长度L，整体结构宽度W，整体结构高度H；第一级波纹夹层结构中内部波纹芯体的斜杆长度l_c1，平台长度l_p1，壁厚t_c1，以及斜杆夹角α₁；第二级波纹夹层结构中内部波纹芯体的斜杆长度l_c2，平台长度l_p2，壁厚t_c2，斜杆夹角α₂，以及上下面板壁厚t_f2。

图  2  多级波纹夹层梁几何图示

Figure  2.  Geometry of the hierarchical corrugated sandwich beam

下载: 全尺寸图片 幻灯片

2.   数值仿真

利用有限元方法对多级波纹夹层结构在泡沫铝子弹冲击下的动态力学性能进行数值计算分析。泡沫子弹冲击方法^[45]一般采用轻气炮发射圆柱形泡沫子弹冲击测试结构，分析结构的动态力学响应，可以在实验室尺度下观测结构在强动冲量载荷下的力学性能及特点^{[10, 46-48]}，大大降低了实验周期，节省了实验成本，提高了实验安全性及可观测性。泡沫子弹的密度为${\rho }_{\mathrm{p}}$，直径为d₀，长度为l₀，当其以初速度v₀沿轴向出射时，单位面积的初始动量为

当子弹冲击到被测结构时，一种类似于空爆或水爆载荷产生的压强时间曲线作用到被测结构^[43]。当被冲击结构为具有有限屈服强度的可变形体时，作用到结构上的单位面积名义冲量可以通过一些可观测的变量进行估算：

式中：v_r为泡沫子弹反弹速度（取正值进行计算）。在实际实验测试中，当子弹的反弹速度相对于子弹初始出射速度而言较小时，则作用到结构上的单位面积名义冲量的估算可以简化为

即作用到结构上的冲量与泡沫子弹的初始动量近似相等。

接下来对数值仿真模型及计算结果进行详细的描述。

2.1   有限元模型

在Abaqus-Explicit分析模块中建立单级波纹夹层结构（ECB）和多级波纹夹层结构（HCB）受泡沫子弹冲击的有限元模型，如图3所示。单级波纹夹层结构的几何尺寸与文献[35]中的空波纹夹层结构尺寸一致，多级波纹夹层结构的几何尺寸在表1中给出。泡沫铝子弹的直径d₀=57 mm，长度l₀=85 mm。

图  3  单级波纹夹层梁（左）和多级波纹夹层梁（右）泡沫子弹冲击有限元模型

Figure  3.  Finite element model of foam projectile impact on the single-level empty corrugated sandwich beam (left) and the hierarchical corrugated sandwich beam (right)

下载: 全尺寸图片 幻灯片

表  1  多级波纹夹层结构几何尺寸

Table  1.  Geometric parameters of the hierarchical sandwich beam

L/mm	W/mm	lc1/mm	lp1/mm	tc1/mm	α1/(°)	lc2/mm	lp2/mm	tc2/mm	α2/(°)	tf2/mm
300	60	20	5	0.5	60	8	2	0.5	60	0.5

下载: 导出CSV 

| 显示表格

为了简化计算，根据对称性，仅建立了四分之一模型，如图3所示。在模型蓝色引线所指示的两个边界处分别设置x方向和y方向的对称边界条件。同时，在蓝色引线所指示的夹层梁末端设置固定边界条件，限制边界上所有节点的转动和平移，用于模拟固支状态。泡沫铝子弹采用实体单元建模，网格类型为线性缩减积分六面体单元（C3DR8），网格大小为2 mm。夹层结构的芯体和面板均采用四边形壳单元（S4R）建模，网格大小为0.5 mm。不考虑面板与芯体之间的脱粘或脱焊现象，故波纹芯体和面板之间通过绑定约束设置为理想连接状态。另外，对所有部件设置通用接触和自接触，由于摩擦力对能量消耗的贡献非常小，所以在仿真中忽略摩擦力的影响。在仿真起始分析步中定义泡沫铝子弹垂直朝向夹层梁结构的初始冲击速度v₀。

2.2   材料属性

模拟时，泡沫铝子弹的材料模型简化为各向同性强化本构模型，利用Abaqus软件中描述可压碎泡沫的Deshpande-Fleck本构模型^[49]进行建模，其中^[35]：泡沫铝密度${\rho }_{\mathrm{p}}$为378 kg/m³，杨氏模量为1 GPa，弹性泊松比为0.3，塑性泊松比为0，压缩屈服应力比为1.732。硬化曲线取自文献[35]。

夹层结构面板和芯体母材均为304不锈钢材料，利用各向同性双线性弹塑性材料模型进行建模。其中，材料的弹性变形行为由弹性模量和泊松比表征，塑性变形行为由切线模量计算得到的塑性应力应变关系定义。具体材料力学性能参数为^[35]：304不锈钢材料密度为7800 kg/m³，杨氏模量为200 GPa，泊松比为0.3，屈服强度为180 MPa，切线模量为2 GPa；通过Cowper-Symonds准则考虑材料的应变率相关性，其关系式为

式中：${\sigma _{\text{d}}}$和${\sigma _0}$分别为动态和静态屈服应力；$\dot \varepsilon$为塑性应变率；C和P为材料应变率相关的力学性能参数，分别取 3398.47 s⁻¹和 6.17。

2.3   数值模拟方法验证

利用数值模拟对夹层结构在泡沫子弹冲击下的过程进行可视化分析时，首先需要对数值仿真模型的可靠性进行验证。将单级波纹夹层结构的计算结果与文献[35]的实验与数值模拟结果进行对比验证。图4给出了单级波纹夹层结构在泡沫子弹以173 m/s的出射速度冲击下的前后面板的跨中挠度时程曲线。结果表明，本文计算结果与文献计算结果吻合较好，其前后面板跨中挠度时程曲线均先迅速增大，达到最大值后由于回弹作用开始轻微下降，然后在一个恒定值附近作弹性波动。取其弹性波动期间最后几个波峰波谷的平均值作为最终挠度，两者的计算结果亦误差较小。进一步地，将本文模拟计算得到的不同子弹动量下单级波纹夹层结构前后面板最终跨中挠度与实验测试结果进行对比。如图5所示，本文模拟结果与实验结果吻合较好，前后面板的最终跨中挠度随子弹初始动量的增加而增加，并且前面板挠度的增加幅度由于芯体压溃程度增加的原因而略大于后面板的增加幅度。

图  4  单级波纹夹层梁的前后面板跨中挠度时程曲线的结果可靠性验证

Figure  4.  Validation of mid-span deflection time histories of impact and rear face sheets for single-level empty corrugated sandwich beam

下载: 全尺寸图片 幻灯片

图  5  单级波纹夹层梁在不同子弹动量作用下前后面板最终跨中挠度值的数值仿真结果与实验结果对比

Figure  5.  Comparison of numerical and experimental results for permanent mid-span deflection values of impact and rear face sheets of single-level empty corrugated sandwich beams under different projectile momentum

下载: 全尺寸图片 幻灯片

图6给出了单级波纹夹层结构在不同子弹动量作用下最终变形模式的数值模拟结果和实验结果（样件编号与文献[35]一致）。结果表明，模拟结果可以对夹层结构在泡沫子弹冲击下的变形破坏模式进行较为精确的预测，能够捕捉到冲击区域芯体压溃、冲击边界到固支边界跨梁区域的芯体剪切、夹层梁整体的非弹性大变形等。当子弹初始动量较小时，冲击区域芯体压溃程度也较小，夹层梁整体呈现出类似弯曲的非弹性大变形。随着初始动量的增加，芯体压溃程度逐渐增大，跨梁区域的芯体剪切程度也有所增加，夹层梁整体变形逐渐呈现拉伸状态，并且由于高冲量作用下的惯性作用，梁的轮廓逐渐由直线变为弧线状态。

图  6  单级波纹夹层梁在不同子弹动量作用下最终变形模式的数值仿真结果与实验结果对比

Figure  6.  Comparison of numerical and experimental results for final deformation modes of single-level empty corrugated sandwich beams under different projectile momentum

下载: 全尺寸图片 幻灯片

虽然本文的结果与之前的实验和数值结果吻合较好，但仍有一些小的误差，如芯体的压溃程度存在微小误差、前后面板最终跨中挠度值存在微小误差、未能模拟芯体和面板之间脱焊的局部变形模式。这些误差大致可以归因于：(1) 本文的模型采取了简化的1/4模型，在相应位置设置了理想的对称边界和固支边界条件，相比于真实的实验测试和全模型计算仍存在小的差异；(2) 模拟中的几何尺寸为理想建模，不考虑实际制备中的几何误差和缺陷；(3) 模拟中不考虑实验中钎焊所增加的焊料质量和体积，且不考虑脱粘或者脱焊现象；(4) 模拟中采用的材料本构是对材料力学行为的数学抽象与简化，与材料真实的力学行为不可避免地存在一些偏差等。

为了分析泡沫子弹冲击过程中的冲量作用过程，图7(a)给出了泡沫铝子弹与单级（ECB）和多级（HCB）波纹夹层结构冲击侧面板的接触压强-时间曲线。选取了泡沫铝子弹冲击速度为100、200、300 m/s共3个值下的结果进行分析。结果表明，当泡沫子弹撞击到夹层结构时，接触压强迅速上升到最大值，然后开始下降，大约在1.2~1.5 ms之间下降到零。单级波纹夹层结构和多级波纹夹层结构与泡沫子弹的接触压强时程曲线的形态基本一致。对该压力曲线进行积分，得到了传递到结构上的单位面积冲量-时间曲线（图7(b)）。可以看出，在相同的子弹初始动量条件下，传递到单级波纹夹层结构和多级波纹夹层结构上的冲量大小基本保持一致。计算最终传递的冲量结果与子弹初始动量的比值，得到了冲量转化比率（图7(c)）。结果表明，与之前讨论一致，作用到结构上的冲量与泡沫子弹的初始动量近似相等，冲量转化比约为1。换句话说，在本文所讨论的冲量范围内，可以直接通过泡沫子弹的初始动量来评估施加到单级和多级波纹夹层结构上的载荷水平。

图  7  泡沫子弹冲击夹层结构的冲量传递过程

Figure  7.  Impulse transfer process of foam projectile impacting sandwich structures

下载: 全尺寸图片 幻灯片

3.   结果与讨论

3.1   结构动态冲击响应

图8给出了多级波纹夹层结构在泡沫子弹冲击下的动态变形过程。从图中可以看出，当泡沫子弹初始动量较小时（图8(a)，M₀=3.21 kPa·s），冲击侧与背侧面板的二级波纹芯体和内部的一级波纹芯体的压溃程度都较小。子弹接触到多级波纹夹层梁后，夹层梁开始变形，但是由于初始动量水平低、芯体压溃程度小，夹层结构的塑性铰传播过程不明显，发生了更加类似于整体弯曲的动态变形响应。随着子弹动量水平增加（图8(b)，M₀=6.43 kPa·s），波纹芯体压溃程度增大，子弹接触到多级波纹夹层梁后，冲击侧面板的二级波纹芯体和内部的一级波纹芯体开始压缩，并在冲击边界处形成塑性铰。随后，塑性铰向中间及两边传播，从冲击边界到固支边界梁跨区域的内部一级波纹芯体发生剪切变形。当塑性铰传播到梁的跨中中心及两边的固支边界处后，停止传播，形成驻行铰（大约在 0.9 ms 处）。之后，梁进一步发生整体的拉伸变形，在大约 1 ms 后达到最大变形，随后开始反弹并进入弹性振动阶段。当泡沫子弹初始动量水平较大时（图8(c)，M₀=9.64 kPa·s），波纹芯体压溃程度进一步增大，并且可以看出压溃过程具有明显的阶段性，大致可以分为2个阶段：第一阶段，泡沫子弹冲击结构后，冲击侧面板的二级波纹芯体率先开始压缩，约 0.1 ms 时受冲击区域的二级波纹芯体被完全压实；第二阶段，继续压缩内部的一级波纹芯体，至 0.4 ms 左右一级波纹芯体也被完全压溃，而背侧面板的二级波纹芯体压溃程度仍然不明显。除此之外，其塑性铰传播、形成驻行铰、整体拉伸至最大变形的动态过程与M₀=6.43 kPa·s条件下类似。

图  8  模拟计算得到的多级波纹夹层梁在泡沫子弹冲击下的动态变形过程

Figure  8.  Numerical simulated structural evolution of hierarchical corrugated sandwich beams under foam projectile impacts

下载: 全尺寸图片 幻灯片

3.2   定量挠度结果

图9 给出了不同子弹动量水平下多级波纹夹层结构受到冲击之后其背侧面板跨中挠度时程曲线。可以看出，与单级波纹夹层结构的跨中挠度时程响应曲线（图4）类似，多级波纹夹层结构中心点挠度在受到冲击之后先迅速上升，达到最大值后开始回弹，然后进入弹性波动阶段。随着子弹初始动量的增加，结构背板中心点挠度最大值和弹性波动稳定值都不断增加，结构响应到达挠度最大值的时间先轻微增大然后基本稳定，但都在 1 ms 左右。

图  9  不同子弹初始动量水平下多级波纹夹层梁背侧面板跨中挠度时程曲线

Figure  9.  Mid-span deflection time histories of the rear face of hierarchical corrugated sandwich beams under different projectile initial momentum

下载: 全尺寸图片 幻灯片

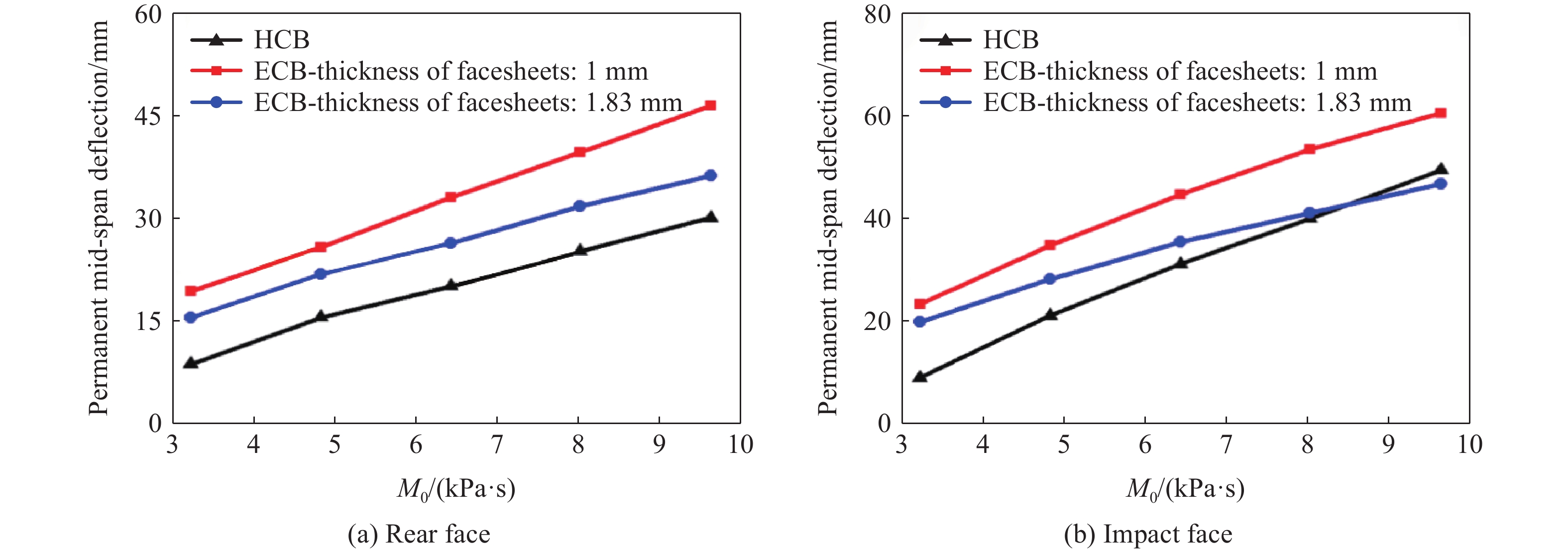
计算单级波纹（ECB）与多级波纹夹层结构（HCB）冲击侧和背侧面板中心点的最终挠度，绘制最终挠度与子弹初始动量的关系曲线，如图10所示。针对 ECB，设计了两种结构尺寸：两种波纹芯体壁厚均与多级波纹夹层结构保持一致为 0.5 mm，设计其中一种的两块面板厚度为 1 mm（与参考文献[35]尺寸一致），另一种面板厚度为 1.83 mm（与多级波纹夹层结构保持等质量）。从图10(a) 中可以看出，对于梁结构背板最终跨中挠度，在本文所探究的子弹初始动量范围内，多级波纹夹层结构挠度值均小于单级波纹夹层结构挠度值（无论是 1 mm 厚度面板条件下还是等质量条件下），表明多级波纹夹层结构具有明显的抗强动冲击防护优势。在较低的冲量水平下（M₀=3.21 kPa·s），其挠度减小的百分比甚至高达51%。如图10(b)所示，对于冲击侧面板的最终跨中挠度而言，多级波纹夹层结构的挠度值始终小于1 mm 厚度面板的单级波纹夹层结构的挠度值，而相对于等质量条件下的单级波纹夹层结构，其挠度值在子弹动量较低的水平下减小明显，但是随着子弹初始动量增加，两者挠度值逐渐趋于近似水平。

图  10  不同子弹初始动量下多级波纹夹层梁（HCB）和两种不同厚度面板的单级波纹夹层梁（ECB）最终跨中挠度

Figure  10.  Mid-span deflection of the hierarchical corrugated sandwich beam (HCB) and two kinds of single-level empty corrugated sandwich beams with different face thicknesses (ECB) impacted by projectiles with different momentum

下载: 全尺寸图片 幻灯片

此外，进一步考虑单级波纹夹层结构与多级波纹夹层结构等质量且等梁高的情形。这种情形下，同样设计了两种结构尺寸：一种是将原单级波纹夹层结构中的波纹芯体等比例放大至目标芯层厚度，调整壁厚使其与多级波纹夹层结构等质量，如此一来改变了梁结构包含的波纹个数；另一种是保持波纹个数不变，改变波纹斜杆倾角及长度使波纹芯体达到目标芯层高度，调整壁厚使其与多级波纹夹层结构等质量。两种单级波纹夹层结构的几何图示如图11所示，波纹芯体具体的几何参数如表2所示。通过数值模拟研究两种夹层梁冲击侧和背侧面板永久跨中挠度与子弹初始动量的关系，结果如图12所示。可以看出，在所研究的子弹动量范围内，两种等芯层厚度的夹层梁的冲击侧与背侧面板跨中挠度均大于多级波纹夹层梁，表明本文所提出的多级波纹夹层结构的抗冲击性能在等质量、等梁高的情形下依然优于单层波纹夹层结构。

图  11  梁ECB-S1（左）和ECB-S2（右）的几何图例

Figure  11.  Geometry of ECB-S1 (left) and ECB-S2 (right)

下载: 全尺寸图片 幻灯片

表  2  单层波纹夹层梁ECB-S1和ECB-S2的几何参数

Table  2.  The geometry parameters of the empty corrugated sandwich beams ECB-S1 and ECB-S2

梁	lp/mm	lc/mm	tc/mm	α/(°)	tf/mm
ECB-S1	9.12	36.46	2.10	60	0.5
ECB-S2	5.00	34.88	1.31	73.34	0.5

下载: 导出CSV 

| 显示表格

图  12  不同子弹初始动量下多级波纹夹层梁（HCB）和等质量等梁高单级波纹夹层梁（ECB）的最终跨中挠度

Figure  12.  Mid-span deflection of the hierarchical corrugated sandwich beam (HCB) and two kinds of single-level empty corrugated sandwich beams with the mass and beam height same to the HCB (ECB) impacted by projectiles with different momentum

下载: 全尺寸图片 幻灯片

3.3   最终变形破坏模式

不同子弹初始动量水平下多级波纹夹层结构遭受强动冲击之后的最终变形破坏模式在图13中给出。当子弹动量较小时（M₀=3.21 kPa·s），夹层梁整体呈现出类似弯曲的变形形态，梁冲击区域至固支边界的跨梁区域内的一级波纹芯体具有明显的剪切变形，同时，冲击侧和背侧面板的二级波纹芯体及内部的一级波纹芯体的压溃程度均不明显。随着子弹动量增加（M₀=4.82, 6.43 kPa·s），夹层梁整体的弯曲变形程度及跨梁区域内部的一级波纹芯体的剪切变形程度均明显增加，夹层梁冲击区域的内部一级波纹芯体产生了明显的压溃，但是冲击侧和背侧面板的二级波纹芯体的压溃程度依旧不明显。当子弹动量继续增加时（M₀=8.03 kPa·s），夹层梁结构整体拉伸的大变形形态逐渐显现，夹层梁冲击区域的内部一级波纹芯体压溃程度进一步增加，冲击侧面板的二级波纹芯体也出现了明显的压溃，压溃程度小于一级波纹芯体，然而背侧面板的二级波纹芯体仍没有明显压溃。当子弹动量水平更大时（M₀=9.64 kPa·s），夹层梁结构整体的大变形进一步增大，夹层梁冲击区域的内部一级波纹芯体几乎已经压实，冲击侧面板的二级波纹芯体压溃程度也大幅增加，背侧面板的二级波纹芯体压溃程度依然很小。总体来看，波纹芯体的压溃变形顺序及变形程度为：夹层结构内部的一级波纹芯体大于冲击侧面板的二级波纹芯体大于背侧面板的二级波纹芯体。

图  13  多级波纹夹层梁在不同动量水平冲击条件下的最终变形破坏模式

Figure  13.  Final deformation modes of hierarchical corrugated sandwich beams under different projectile momentum

下载: 全尺寸图片 幻灯片

3.4   能量吸收分析

不同初始子弹动量冲击下，多级波纹夹层梁各部件的最终塑性应变能如图14所示。图14(a)表明，随着子弹动量的增加，多级波纹夹层梁整体的塑性应变能不断增加，代表着结构的塑性大变形不断增大。结构各部件中，内部的一级波纹芯体和冲击侧面板的二级波纹芯体吸收能量较多，而背侧三明治面板整体吸收能量均比较少。进一步计算多级波纹夹层梁各部件塑性应变能的能量占比，如图14(b)所示，当子弹动量较小时（M₀=3.21 kPa·s），夹层结构内部的一级波纹芯体塑性应变能占比最大，高达36%，而背侧夹层面板各部件能量占比最小，总体占比仅为26%。随着子弹初始动量的增加，夹层结构内部的一级波纹芯体的能量占比逐步降低，从36%降至23%。而冲击侧夹层面板整体的能量占比不断增大，其中冲击侧面板内部的二级波纹芯体能量占比上升明显，从12%上升至28%，替代了夹层结构内部的一级波纹芯体，成为多级波纹夹层梁结构塑性应变能占比最大的部件。而对于冲击侧夹层面板的子面板，其靠近冲击侧的子面板能量占比几乎不变，远离冲击侧的子面板能量占比有轻微增加。背侧夹层面板整体的塑性应变能占比有轻微下降，其中靠近冲击侧的子面板和内部的二级波纹芯体变化不大，主要是远离冲击侧的子面板能量占比下降导致的。该结果与第3.3节的变形模式分析结果相互印证，对于多级波纹夹层梁而言，其内部的一级波纹芯体和冲击侧夹层面板中的二级波纹芯体压溃程度明显大于背侧面板中的二级波纹芯体，并且随着冲量水平的增加，芯体压溃水平增加。同时，跨梁区域的芯体产生剪切变形，而冲击侧夹层面板中的波纹芯体的剪切变形沿着波纹芯体的轴向产生，随着冲量水平的增加，其可以吸收更多的能量，因此冲击侧夹层面板中的二级波纹芯体塑性应变能占比不断增大，最终超过梁结构内部的一级波纹芯体的塑性应变能占比。

图  14  多级波纹夹层梁各部件最终塑性应变能及能量比率对比

Figure  14.  Final plastic strain energy and energy ratio of each part of hierarchical corrugated sandwich beams

下载: 全尺寸图片 幻灯片

3.5   增强机理分析

当夹层梁结构受到局部冲击强动载荷之后，其内部芯体的吸能能力和结构整体的极限抗弯能力与极限抗拉能力是影响结构最终变形挠度大小的关键因素^{[2-3, 50]}。对于本文研究的多级波纹夹层梁结构而言，由于在夹层结构的前后面板中引入了多级夹层设计，增加了夹层结构的多孔吸能部件。并且，根据前文分析结果可知，冲击侧夹层面板在压溃吸能中发挥了较大作用，随着子弹动量水平的增加，其吸能占比也不断增大。其与夹层结构内部的一级波纹芯体的压溃吸能共同作用，对背侧面板提供了很好的保护。另外，多级波纹夹层结构的设计中，两侧夹层面板中的二级波纹芯体的轴向与夹层结构轴向平行，从而保持了夹层结构的极限抗拉性能。与此同时，多级的设计增加了夹层梁的总厚度，从而增大了夹层梁的极限抗弯能力，扩大了夹层结构的塑性屈服面^{[2, 50]}，增强了结构的抗强动冲击性能。

4.   结　论

本文研究了多级波纹夹层梁结构在泡沫子弹冲击作用下的动态力学行为，重点分析了结构的动态变形过程、变形大小、最终变形破坏模式和能量吸收特性，讨论了结构抗冲击性能的内在力学机理。结果表明：

(1) 多级波纹芯体夹层梁在受到泡沫子弹冲击后，冲击侧夹层面板内部的二级波纹芯体先开始压溃，内部的一级波纹芯体紧接着开始压缩变形，背侧夹层面板内部的二级波纹芯体压溃不明显；在冲击边界形成塑性铰后，塑性铰向中间及两边开始传播，达到中心点和固支边界后，形成驻行铰，结构整体开始拉伸变形，达到最大变形后，进入回弹阶段；

(2) 多级波纹芯体夹层梁背侧面板的最终跨中挠度在本文所研究的子弹动量水平范围内始终小于单级波纹夹层梁背侧面板的最终跨中挠度，即使在等质量条件下，仍然具有明显的抗冲击防护性能优势；对于冲击侧面板的最终跨中挠度，多级波纹芯体夹层梁在较小冲量水平下挠度减小明显，随着子弹冲量水平增加，多级波纹芯体夹层梁和等质量单级波纹芯体夹层梁冲击侧面板的最终跨中挠度趋于近似水平；

(3) 多级波纹芯体夹层梁受到泡沫子弹冲击后的最终变形破坏模式主要包括——夹层梁整体的非弹性大变形（如子弹动量较小时，呈现类似弯曲变形形态，子弹动量较大时，呈现梁整体的拉伸大变形形态）、冲击区域一二级波纹芯体的压缩变形、梁跨区域一二级波纹芯体的剪切变形；在所研究的子弹动量水平范围内，背侧夹层面板内部的二级波纹芯体的变形始终不明显；

(4) 多级波纹芯体夹层梁的最终塑性应变能随着子弹动量水平增加而不断增大，表明塑性变形不断增大；对于各部件塑性应变能占比，一级波纹芯体和冲击侧夹层面板内的二级波纹芯体两者占比较高，并且随着子弹动量水平增加，一级波纹芯体的能量占比下降，而冲击侧夹层面板，尤其是其内部的二级波纹芯体的能量占比上升；

(5) 多级波纹芯体夹层梁相比于等质量单级波纹芯体夹层梁具有明显的抗冲击防护性能优势，主要归因于——(a) 多级夹层设计增加了结构的多孔芯体，冲击侧夹层结构内部的二级波纹芯体和一级波纹芯体的压溃吸能为背侧面板提供了很好的保护；(b) 冲击侧和背侧夹层面板内部的二级波纹芯体的轴向与夹层梁的轴向平行，很好地保持了夹层结构的极限抗拉性能；(c) 当单级波纹夹层结构不与其等梁高时，多级夹层设计增加了夹层梁的总厚度，从而增大了夹层梁的极限抗弯性能，扩大了夹层梁的塑性屈服面。

感谢中国水利水电建设工程咨询西北有限公司对本文的支持。