Bending waves excited by bending fractures of brittle beams
-
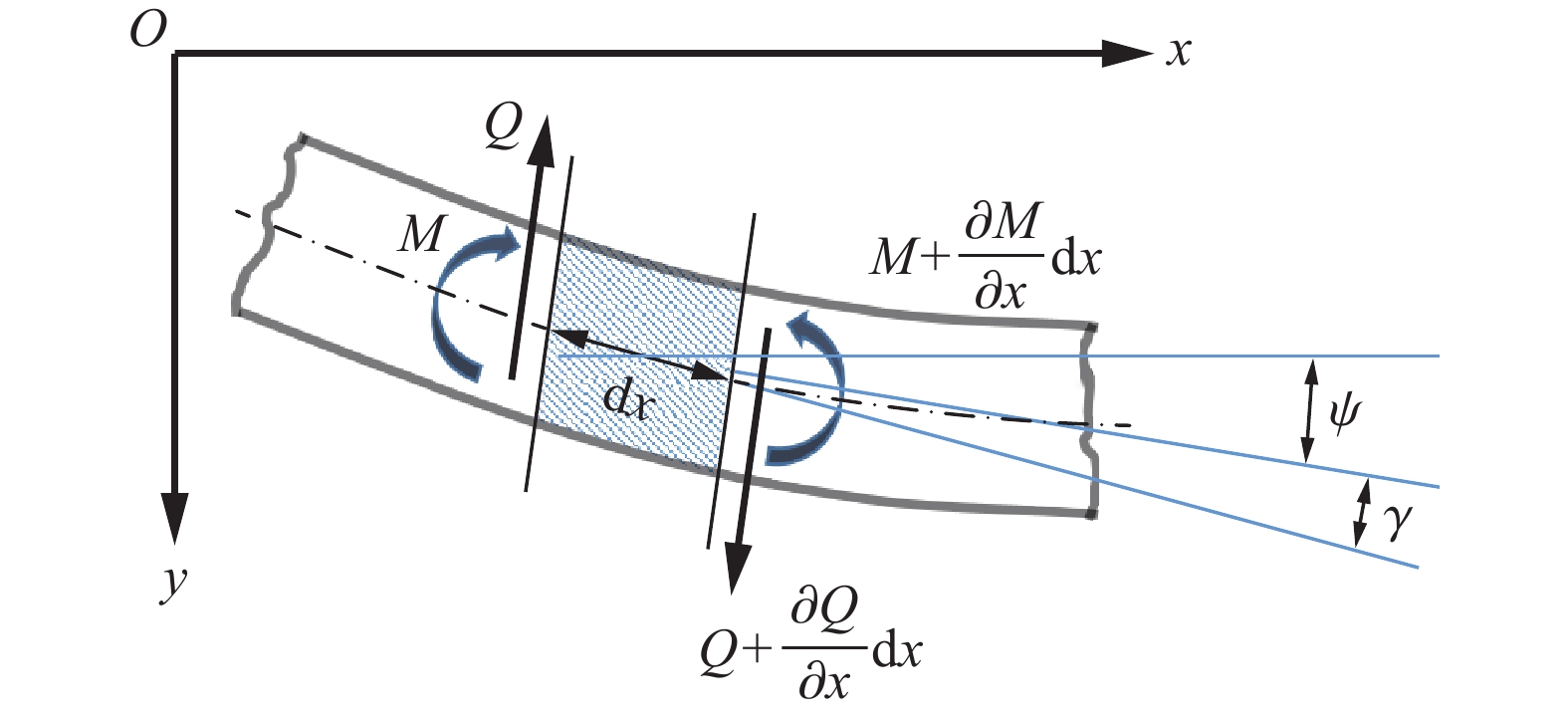
摘要: 脆性细长结构在弯曲载荷作用下突然断裂，可能导致断裂点附近出现二次断裂。传统的Euler-Bernoulli梁理论难以描述突加载荷或突卸载荷所导致的波动现象，而Timoshenko梁中的弯曲波速度为有限值，具有一个内禀特征时间，因此基于Timoshenko梁理论来分析弹性梁的弯曲断裂问题。使用Timoshenko梁理论，结合一个包含断裂能的脆性内聚力弯曲断裂模型，建立一维弯曲波传播问题的初边值问题，采用特征线方法求解3种边界条件下半无限长梁中卸载弯曲波的传播问题；进一步分析了断裂能对断裂时间以及峰值弯矩的影响，然后通过数值计算给出这3种情况下梁的动力学响应过程。研究结果表明：处于纯弯曲状态的梁一旦发生瞬时断裂，二次断裂发生点距离初次断裂点的最短距离为梁截面回转半径的5倍，因为该距离以内的弯矩不会出现过冲；最有可能发生二次断裂的位置与无量纲断裂能和无量纲开裂角度有关，在距离初始断裂点17.7个特征长度的位置会产生幅值达到1.67倍初始弯矩的峰值弯矩；较大的断裂能将延长断裂时间，导致弯矩峰值点位置偏远，相应的峰值载荷也降低。Abstract: Under pure bending, a brittle slender beam may undergo sudden fracture, leading to the occurrence of secondary fractures near the initial fracture point. Studies suggest that the secondary fractures are induced by the unloading bending wave released from the initial fracture. Unloading causes an overshoot of the bending moment near the location of the initial fracture. Traditional Euler-Bernoulli beam theory cannot describe the wave propagation phenomena resulting from sudden loading or unloading. In this paper, the bending fracture problem is analyzed based on Timoshenko beam theory. In this theory, the bending wave velocity is finite, and it possesses an intrinsic characteristic time. Utilizing Timoshenko beam theory and incorporating a brittle cohesive bending fracture model containing fracture energy, an initial-boundary value problem is established for the one-dimensional propagation of bending waves. The problem with three boundary conditions is solved using the characteristic line method: (1) the beam is suddenly applied with a boundary transverse velocity; (2) the beam is suddenly applied with a boundary bending moment; (3) the beam initially bears a constant moment, which is released according to a cohesive bending fracture law. Through numerical calculations, the dynamic responses of the beam under these three conditions are presented. Initially, the problems (1) and (2) are calculated using the characteristic line method, validating the feasibility of this approach. Subsequently, by calculating problem (3), the impact of fracture energy on fracture time and peak moment is analyzed. The study reveals that once a beam in a pure bending state undergoes instantaneous fracture, the shortest distance between the point of secondary fracture and the point of primary fracture is 5 times characteristic length. When the non-dimensional fracture energy is 1.4×10−4, the location at 17.7 characteristic lengths from the initial fracture point exhibits a peak moment with an amplitude of 1.67, making it the most likely position for secondary fracture. Larger fracture energy prolongs the fracture time, resulting in a more distant peak moment position and a corresponding reduction in peak load.
-
图 4 初始静止、不受力梁左端受突加载荷作用问题
Figure 4. Left end of unstressed beam subjected to a sudden applied load with initial static state
图 5 本文与文献[11]在
$ x=0, 5 $ 位置的剪力时程对比图Figure 5. Variation with time of the shear force at
$ x=0, 5 $ compared with analytical solution in reference [11]
图 6 本文与文献[11]在
$ t=5, 10 $ 时刻的剪力波形对比Figure 6. Variation with position of the shear force at
$ t=5, 10 $ compared with analytical solution in reference [11]
图 7 本文与文献[11]在
$ t=5 $ 时刻的速度和弯矩波形对比Figure 7. Variation with position of the velocity and the bending moment at
$ t=5 $ compared with analytical solution in reference [11]
图 8 不受力梁边界受突加弯矩作用时的弯曲波传播对比
Figure 8. Bending wave propagations in a Timoshenko beam subjected to a suddenly applied boundary moment compared with analytical solution
图 9 静止梁边界受突加弯矩作用时的剪力传播对比
Figure 9. Shear wave propagations in a Timoshenko beam subjected to a suddenly applied boundary moment compared with analytical solution
图 10 初始静止处于纯弯曲状态的梁突然断裂时与卸载波相关的弯矩分布
Figure 10. Bending moment profiles in a Timoshenko beam suddenly broken under pure bending
图 11 耦合裂纹开裂角度与所受弯矩的内聚力断裂模型
Figure 11. Cohesive fracture model coupling bending moment and cracking opening angle
图 12 不同断裂能下的线性弯曲断裂模型
Figure 12. Model of linear flexural fracture at different fracture energies
图 13 断裂点（边界点）的弯矩
$ M\left(t\right) $ 时程曲线Figure 13. History curves of bending moment
$ M\left(t\right) $ at the break point (boundary)
图 14 不同断裂能下各个时刻的弯矩波形
Figure 14. Bending wave propagations at different fracture energies
图 15 不同断裂能下断裂导致邻近区域弯矩过冲峰值的空间分布包络线
Figure 15. Envelope of the overshot bending moment in a brittle beam when it breaks with different cohesive fracture energy
表 1 不同断裂能（开裂角度）下峰值弯矩极值的时空坐标
Table 1. Positions and time of peak bending moment extremes at different fracture energies (cracking angles)
开裂角度
θc归一化峰值弯矩极值
Mp = Mmax/m0峰值弯矩
位置xc峰值弯矩
时间tc0.004 1.668 17.67 32.95 0.008 1.657 17.68 34.33 0.012 1.639 17.72 35.90 
下载: 导出CSV
表 2 意大利面断裂峰值弯矩极值的时空坐标
Table 2. Positions and time of peak bending moment extremes of spaghetti
开裂角度θc/rad 断裂能Gc/μJ 峰值弯矩位置xc/mm 峰值弯矩时间tc/μs 0.004 12.8 5.10 5.97 0.008 25.6 5.10 6.23 0.012 38.4 5.12 6.51
下载: 导出CSV
-
[1] FEYNMAN R P, SYKES C. No ordinary genius: the illustrated Richard Feynman [M]. New York: Norton, 1994: 180–181. [2] SCHINDLER H J, KOLSKY H. Multiple fractures produced by the bending of brittle beams [J]. Journal of the Mechanics and Physics of Solids, 1983, 31(5): 427–436. DOI: 10.1016/0022-5096(83)90008-X. [3] AUDOLY B, NEUKIRCH S. Fragmentation of rods by cascading cracks: why spaghetti does not break in half [J]. Physical Review Letters, 2005, 95(9): 095505. DOI: 10.1103/PhysRevLett.95.095505. [4] TIMOSHENKO S P. On the correction for shear of the differential equation for transverse vibrations of prismatic bars [J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1921, 41(245): 744–746. DOI: 10.1080/14786442108636264. [5] 龙龙, 郑宇轩, 周风华, 等. 铁木辛柯梁中的卸载弯曲波及二次断裂 [J]. 力学学报, 2021, 53(6): 1658–1670. DOI: 10.6052/0459-1879-21-106.LONG L, ZHENG Y X, ZHOU F H, et al. Unloading flexural stress wave in a Timoshenko beam and the secondary fracture of the beam [J]. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(6): 1658–1670. DOI: 10.6052/0459-1879-21-106. [6] 李永池. 波动力学[M]. 2版. 合肥: 中国科学技术大学出版社, 2018: 9–10. [7] 李凤云. 脆性梁的弯曲波传播问题研究[D]. 浙江宁波: 宁波大学, 2018: 8–28.LI F Y. Flexural wave propagation in brittle material[D]. Ningbo University. 2018: 8–28. [8] LEONARD R W, BUDIANSKY B. On traveling waves in beams: NACA-TR-1173 [R]. USA: NASA, 1954. [9] AL-MOUSAWI M M. Transient response of Timoshenko beams with discontinuities of cross-section [J]. International Journal of Mechanical Sciences, 1984, 26(4): 277–292. DOI: 10.1016/0020-7403(84)90048-1. [10] AL-MOUSAWI M M. On experimental studies of longitudinal and flexural wave propagations: an annotated bibliography [J]. Applied Mechanics Reviews, 1986, 39(6): 853–865. DOI: 10.1115/1.3149516. [11] BOLEY B A, CHAO C C. Some solutions of the Timoshenko beam equations [J]. Journal of Applied Mechanics, 1955, 22(4): 579–586. DOI: 10.1115/1.4011158. [12] MORTON K W, MAYERS D F. Numerical solution of partial differential equations [M]. New York: Cambridge University Press, 2005: 89–93. [13] KIPP M E, GRADY D E. Dynamic fracture growth and interaction in one dimension [J]. Journal of the Mechanics and Physics of Solids, 1985, 33(4): 399–415. DOI: 10.1016/0022-5096(85)90036-5. [14] HEISSER R H, PATIL V P, STOOP N, et al. Controlling fracture cascades through twisting and quenching [J]. Proceedings of the National Academy of Sciences, 2018, 115(35): 8665–8670. DOI: 10.1073/pnas.1802831115. [15] 龙龙. 弯曲断裂和弯曲应力波的相关问题研究[D]. 浙江宁波: 宁波大学, 2021: 75–108.LONG L. Research on flexural fracture and flexural stress wave [D]. Ningbo University, 2021: 75–108. -
计量
- 文章访问数: 58
- HTML全文浏览量: 25
- PDF下载量: 25
- 被引次数: 0