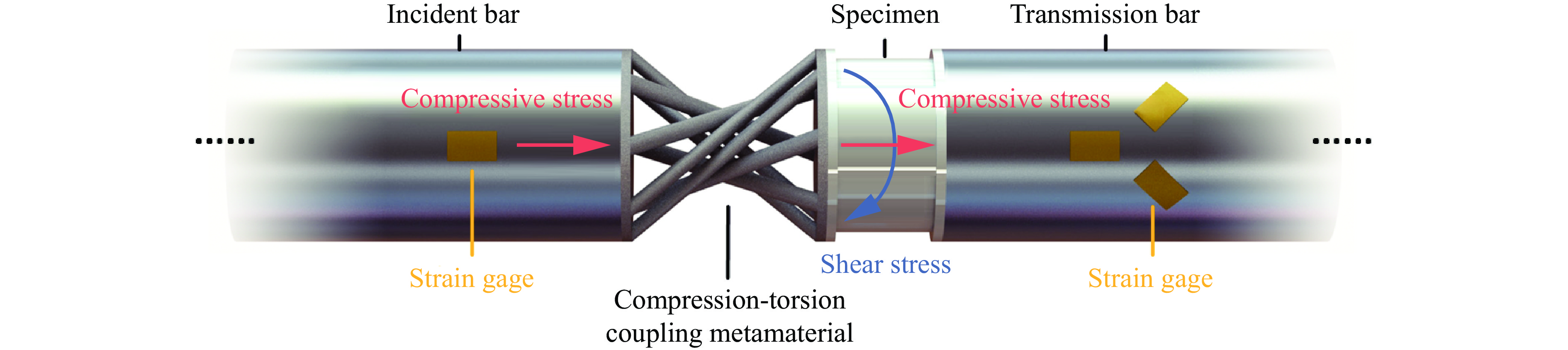
A new experimental technique of dynamic compression-shear combined loading based on metamaterials
-
摘要: 材料或结构在动态压剪复合加载条件下的力学性能对于其工程应用具有重要影响。然而，现有的动态复合加载实验技术存在压缩波和剪切波难以同步施加到试件、实验设备昂贵等问题。本文中利用压扭超材料进行应力波转化，在一维分离式霍普金森压杆（split Hopkinson pressure bar，SHPB）上实现动态压剪同步复合加载。该实验技术具有荷载精准同步、剪压比可控、简单便捷、低成本等优点。针对当压扭超材料转化出来的扭转波幅值较大，透射杆惯性约束不足情况下出现的扭转信号三角波的问题进行详细讨论，并提出相应的解决方案。选用屈服应力各不相同的金属钛、304不锈钢和316L不锈钢等3种材料进行了实验测试，证实了动态压剪同步复合加载技术的有效性。借助有限元模型，深入分析压扭超材料的几何参数对其压扭系数及承载能力的影响，并结合实验结果讨论了该实验技术的适用范围，预测动态压剪同步复合加载技术能测试的材料强度可达约1 GPa，施加给试件的剪压比可达1.18。Abstract: The mechanical properties of materials or structures under dynamic compression-shear combined loading conditions significantly influence their engineering applications. However, existing experimental methodologies for dynamic combined loading confront challenges, such as the difficulty in synchronously applying compression and shear waves to test specimens, in addition to the high cost of experimental equipment. This study introduces a novel experimental technique that utilizes compression-torsion coupling metamaterials for the conversion of stress waves, enabling synchronous dynamic compression-shear combined loading on a one-dimensional Hopkinson pressure bar. This technique offers several advantages, including precise load synchronization, a controllable shear-compression ratio, simplicity, convenience, and low cost. A detailed discussion is presented on the issue of triangular torsion signals that arise when the amplitude of torsional waves converted from compression-torsion metamaterials reaches considerable levels, coupled with insufficient inertial confinement in the transmission bar of the split Hopkinson pressure bar system. Additionally, corresponding solutions to this issue are proposed. Experimental tests were conducted on three materials with distinct yield stresses: titanium, 304 stainless steel, and 316L stainless steel, validating the effectiveness of this experimental technique. Furthermore, leveraging finite element models, an in-depth analysis was conducted on the influence of the geometric parameters of the compression-torsion coupling metamaterials on their compression-torsion coefficients and load-bearing capacities. By integrating these findings with experimental results, the applicability of this experimental technique was discussed, predicting its capability to test materials with strengths up to approximately 1 GPa and to apply shear-compression ratios up to 1.18 to specimens, providing a reference for its application in a broader range of fields. This innovative integration of metamaterials with traditional experimental equipment opens up new avenues for realizing more complex dynamic loading experiments.
-
图 2 压扭超材料的几何参数约束
Figure 2. Geometric parameter constraints of the compression-torsion metamaterials
图 3 压扭超材料的准静态有限元模型示例
Figure 3. Example of the quasi-static finite element model of the compression-torsion metamaterial
图 4 准静态有限元计算结果分析示例
Figure 4. Examples of quasi-static finite element calculation results analysis
图 5 承载能力和压扭系数与斜杆数量关系曲线
Figure 5. Relation of bearing capacity and compression-torsion coefficient with respect to the number of inclined rods number
图 6 承载能力和压扭系数与斜杆倾斜角度关系
Figure 6. Relation of bearing capacity and compression-torsion coefficient with the tilt angle of inclined rods
图 7 承载能力和压扭系数与斜杆直径关系
Figure 7. Relation of bearing capacity and compression-torsion coefficient with respect to the diameter of inclined rods
图 8 承载能力和压扭系数与斜杆长度关系
Figure 8. Relation of bearing capacity and compression-torsion coefficient with respect to the length of inclined rods
图 9 不同斜杆倾斜角度下压扭系数与斜杆长度关系
Figure 9. Relationship curves between the compression-torsion coefficient and the length of inclined rods under different tilt angles of inclined rods
图 10 压扭超材料和SHPB有限元模型示例
Figure 10. Example of the finite element model of compression-torsion metamaterial and SHPB
图 11 Ti6Al4V钛合金的准静态拉伸实验曲线及其拟合曲线
Figure 11. Quasi-static tensile experiment curve and its fitting curve of Ti6Al4V titanium alloy
图 12 SHPB系统的有限元模拟与实验结果对比 （D=20 mm）
Figure 12. Comparison between FEM and experimental results in SHPB system (D=20 mm)
图 13 不同斜杆直径和透射杆直径的SHPB系统有限元分析结果
Figure 13. FEM results of SHPB systems with different diameters of inclined rods and different diameters of transmission bars
图 14 SHPB系统的有限元模拟与实验结果对比（D=50 mm）
Figure 14. Comparison between FEM and experimental results in SHPB system (D=50 mm)
图 16 动态压缩-扭转实验下弹性应变范围内（压缩应变0.002 8）薄壁圆筒钛试件的DIC压缩应变云图和剪切应变云图
Figure 16. Cloud maps of compression strain and shear strain obtained from DIC for a thin-walled cylinder titanium specimen in elastic strain range (compression strain 0.002 8) under dynamic compression-torsion experiments
图 17 动态压缩-扭转实验下塑性应变范围内（压缩应变0.004 9）薄壁圆筒钛试件的DIC压缩应变和剪切应变云图
Figure 17. Cloud maps of compression strain and shear strain obtained from DIC for a thin-walled cylinder titanium specimen in plastic strain range (compression strain 0.004 9) under dynamic compression-torsion experiments
图 18 钛动态压缩-扭转实验的应变率-应变曲线
Figure 18. Strain rate-strain curves of titanium under dynamic compression-torsion experiments
图 19 钛动态压缩-扭转实验的应力-应变曲线
Figure 19. Stress-strain curves of titanium under dynamic compression-torsion experiments
图 20 准静态条件下304不锈钢的压缩应力-应变曲线
Figure 20. Compressive stress-strain curves of 304 stainless steel under quasi-static conditions
图 21 304不锈钢动态压缩-扭转实验的应力-应变曲线
Figure 21. Stress-strain curves of 304 stainless steel under dynamic compression-torsion experiments
图 22 316L不锈钢动态压缩-扭转实验的应力-应变曲线
Figure 22. Stress-strain curves of 316L stainless steel under dynamic compression-torsion experiments
图 23 压扭超材料能提供的扭矩和轴向载荷范围
Figure 23. Range of torque and axial loads that compression-torsion metamaterials can provide
图 24 基于压扭超材料的动态复合加载技术应用范围
Figure 24. Application range of the dynamic combined loading technique based on the compression-torsion metamaterials
表 1 有限元模型采用的材料参数
Table 1. Material parameters used in the finite element model
材料 密度/
(g∙cm−3)弹性模量/
GPa屈服应力/
MPa泊松比 7075铝合金 2.85 71 0.33 Ti6Al4V钛合金 4.40 120 910 0.33 
下载: 导出CSV
表 2 钛的动态压缩-扭转实验结果
Table 2. Dynamic compression-torsion experiment results of titanium
试件编号 $ \theta $/(°) $ {\sigma }_{\mathrm{s}} $/MPa $ {\tau }_{\mathrm{s}} $/MPa $ {\sigma }_{\mathrm{y}} $/MPa 1 70 453.58 117.01 496.80 2 70 429.49 126.49 482.15 3 60 374.31 174.72 481.34 4 60 382.43 180.40 493.84 5 50 346.23 198.34 487.74
下载: 导出CSV
表 3 304不锈钢的动态压缩-扭转实验结果
Table 3. Dynamic compression-torsion experiment results of 304 stainless steel
试件编号 $ \theta $/(°) $ {\sigma }_{\mathrm{s}} $/MPa $ {\tau }_{\mathrm{s}} $/MPa $ {\sigma }_{\mathrm{y}} $/MPa 1 70 350.08 125.87 412.42 2 60 305.43 160.12 412.56
下载: 导出CSV
表 4 316L不锈钢的动态压缩-扭转实验结果
Table 4. Dynamic compression-torsion experiment results of 316L stainless steel
试件编号 $ \theta $/(°) $ {\sigma }_{\mathrm{s}} $/MPa $ {\tau }_{\mathrm{s}} $/MPa $ {\sigma }_{\mathrm{y}} $/MPa 1 70 471.19 172.86 558.27 2 60 440.02 221.21 583.45 3 50 402.85 237.92 576.28
下载: 导出CSV
-
[1] 胡时胜, 王礼立, 宋力, 等. Hopkinson压杆技术在中国的发展回顾 [J]. 爆炸与冲击, 2014, 34(6): 641–657. DOI: 10.11883/1001-1455(2014)06-0641-17.HU S S, WANG L L, SONG L, et al. Review of the development of Hopkinson pressure bar technique in China [J]. Explosion and Shock Waves, 2014, 34(6): 641–657. DOI: 10.11883/1001-1455(2014)06-0641-17. [2] SILVA C M A, ROSA P A R, MARTINS P A F. An innovative electromagnetic compressive split Hopkinson bar [J]. International Journal of Mechanics and Materials in Design, 2009, 5: 281–288. DOI: 10.1007/s10999-009-9101-y. [3] 谢若泽, 卢子兴, 田常津, 等. 聚氨酯泡沫塑料动态剪切力学行为的研究 [J]. 爆炸与冲击, 1999, 19(4): 315–321. DOI: 10.11883/1001-1455(1999)04-0315-7.XIE R Z, LU Z X, TIAN C J, et al. Studies of dynamic shear mechanical properties of PUR foamed plastics [J]. Explosion and Shock Waves, 1999, 19(4): 315–321. DOI: 10.11883/1001-1455(1999)04-0315-7. [4] DUFFY J, CAMPBELL J D, HAWLEY R H. On the use of a torsional split Hopkinson bar to study rate effects in 1100-0 aluminum [J]. 1971, 38(1): 83–91. DOI: 10.1115/1.3408771. [5] CAMPBELL J D, DOWLING A R. The behaviour of materials subjected to dynamic incremental shear loading [J]. Journal of the Mechanics and Physics of Solids, 1970, 18(1): 43–63. DOI: 10.1016/0022-5096(70)90013-X. [6] BAKER W E, YEW C H. Strain-rate effects in the propagation of torsional plastic waves [J]. 1966, 33(4): 917–923. DOI: 10.1115/1.3625202. [7] ELIBOL C, WAGNER M F X. Strain rate effects on the localization of the stress-induced martensitic transformation in pseudoelastic NiTi under uniaxial tension, compression and compression-shear [J]. Materials Science and Engineering: A, 2015, 643: 194–202. DOI: 10.1016/j.msea.2015.07.039. [8] 秦彩芳, 许泽建, 窦旺, 等. 金属材料在复杂应力状态下的塑性流动特性及本构模型 [J]. 爆炸与冲击, 2022, 42(9): 091404. DOI: 10.11883/bzycj-2021-0308.QIN C F, XU Z J, DOU W, et al. Plastic flow properties and constitutive model of metallic materials under complex stress states [J]. Explosion and Shock Waves, 2022, 42(9): 091404. DOI: 10.11883/bzycj-2021-0308. [9] 姚国文, 刘占芳, 黄培彦. 压剪复合冲击下氧化铝陶瓷的剪切响应实验研究 [J]. 爆炸与冲击, 2005, 25(2): 119–124. DOI: 10.11883/1001-1455(2005)02-0119-06.YAO G W, LIU Z F, HUANG P Y. Experimental study on shear response of alumina under combined compression and shear loading [J]. Explosion And Shock Waves, 2005, 25(2): 119–124. DOI: 10.11883/1001-1455(2005)02-0119-06. [10] LEWIS J L, GOLDSMITH W. A biaxial split Hopkinson bar for simultaneous torsion and compression [J]. Review of Scientific Instruments, 1973, 44(7): 811–813. DOI: 10.1063/1.1686253. [11] HARTMANN K H, KUNZE H D, MEYER L W. Shock waves and high-strain-rate phenomena in metals: concepts and applications [M]. Boston: Springer, 1981: 325–337. DOI: 10.1007/978-1-4613-3219-0_21. [12] RITTEL D, LEE S, RAVICHANDRAN G. A shear-compression specimen for large strain testing [J]. Experimental Mechanics, 2002, 42: 58–64. DOI: 10.1007/BF02411052. [13] MEYER L W, STASKEWITSCH E, BURBLIES A. Adiabatic shear failure under biaxial dynamic compression/shear loading [J]. Mechanics of Materials, 1994, 17(2/3): 203–214. DOI: 10.1016/0167-6636(94)90060-4. [14] HOU B, ONO A, ABDENNADHER S, et al. Impact behavior of honeycombs under combined shear-compression. Part Ⅰ: experiments [J]. International Journal of Solids and Structures, 2011, 48(5): 687–697. DOI: 10.1016/j.ijsolstr.2010.11.005. [15] 郑文, 徐松林, 蔡超, 等. 基于Hopkinson压杆的动态压剪复合加载实验研究 [J]. 力学学报, 2012, 44(1): 124–131. DOI: 10.6052/0459-1879-2012-1-lxxb2011-103.ZHENG W, XU S L, CAI C, et al. A study of dynamic combined compression-shear loading technique based on Hopkinson pressure bar [J]. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(1): 124–131. DOI: 10.6052/0459-1879-2012-1-lxxb2011-103. [16] 崔云霄, 卢芳云, 林玉亮, 等. 一种新的高应变率复合压剪实验技术 [J]. 实验力学, 2006(5): 584–590. DOI: 10.3969/j.issn.1001-4888.2006.05.007.CUI Y X, LU F Y, LIN Y L, et al. A new combined compression-shear loading technique at high strain rates [J]. Journal of Experimental Mechanics, 2006(5): 584–590. DOI: 10.3969/j.issn.1001-4888.2006.05.007. [17] 赵鹏铎, 卢芳云, 陈荣, 等. 光通量法在SHPSB剪切应变测量中的应用 [J]. 爆炸与冲击, 2011, 31(3): 232–236. DOI: 10.11883/1001-1455(2011)03-0232-05.ZHAO P D, LU F Y, CHEN R, et al. Luminous flux method for measuring shear strain of the specimen in SHPSB [J]. Explosion and Shock Waves, 2011, 31(3): 232–236. DOI: 10.11883/1001-1455(2011)03-0232-05. [18] NIE H L, SUO T, SHI X P, et al. Symmetric split Hopkinson compression and tension tests using synchronized electromagnetic stress pulse generators [J]. International Journal of Impact Engineering, 2018, 122: 73–82. DOI: 10.1016/j.ijimpeng.2018.08.004. [19] LIU C L, WANG W B, SUO T, et al. Achieving combined tension-torsion split Hopkinson bar test based on electromagnetic loading [J]. International Journal of Impact Engineering, 2022, 168: 104287. DOI: 10.1016/j.ijimpeng.2022.104287. [20] 王维斌, 索涛, 郭亚洲, 等. 电磁霍普金森杆实验技术及研究进展 [J]. 力学进展, 2021, 51(4): 729–754. DOI: 10.6052/1000-0992-20-024.WANG W B, SUO T, GUO Y Z, et al. Experimental technique and research progress of electromagnetic Hopkinson bar [J]. Advances in Mechanics, 2021, 51(4): 729–754. DOI: 10.6052/1000-0992-20-024. [21] JOHNSON J N. Shock propagation produced by planar impact in linearly elastic anisotropic media [J]. Journal of Applied Physics, 1971, 42(13): 5522–5530. DOI: 10.1063/1.1659974. [22] FRENZEL T, KADIC M, WEGENER M. Three-dimensional mechanical metamaterials with a twist [J]. Science, 2017, 358(6366): 1072–1074. DOI: 10.1126/science.aao4640. [23] FERNANDEZ-CORBATON I, ROCKSTUHL C, ZIEMKE P, et al. New twists of 3D chiral metamaterials [J]. Advanced Materials, 2019, 31(26): 1807742. DOI: 10.1002/adma.201807742. [24] XU W Y, ZHOU C, ZHANG H Y, et al. A flexible design framework for lattice-based chiral mechanical metamaterials considering dynamic energy absorption [J]. Thin-Walled Structures, 2024: 112108. DOI: 10.1016/j.tws.2024.112108. [25] MENG L, ZHONG M Z, GAO Y S, et al. Impact resisting mechanism of tension-torsion coupling metamaterials [J]. International Journal of Mechanical Sciences, 2024, 272: 109100. DOI: 10.1016/j.ijmecsci.2024.109100. [26] WANG S A, DENG C, OJO O, et al. Design and testing of a DNA-like torsional structure for energy absorption [J]. Materials & Design, 2023, 226: 111642. DOI: 10.1016/j.matdes.2023.111642. [27] WEI Y C, HUANG C Y, REN L Q, et al. Topological study about deformation behavior and energy absorption performances of 3D chiral structures under dynamic impacts [J]. The Journal of Strain Analysis for Engineering Design, 2023, 58(3): 208–220. DOI: 10.1177/03093247221101803. [28] PARK J, LEE G, KWON H, et al. All-polarized elastic wave attenuation and harvesting via chiral mechanical metamaterials [J]. Advanced Functional Materials, 2024: 2403550. DOI: 10.1002/adfm.202403550. [29] OU H F, HU L L, WANG Y B, et al. High-efficient and reusable impact mitigation metamaterial based on compression-torsion coupling mechanism [J]. Journal of the Mechanics and Physics of Solids, 2024, 186: 105594. DOI: 10.1016/j.jmps.2024.105594. [30] LI Y L, ZHANG H Q. Theoretical analysis on topological interface states of 1D compression-torsion coupling metamaterial [J]. Composite Structures, 2023, 305: 116556. DOI: 10.1016/j.compstruct.2022.116556. [31] WANG Y B, OU H F, HU L L. New type of overrunning clutch based on curved-plate compression-torsion metamaterial [J]. Acta Mechanica Sinica, 2024, 40(8): 423608. DOI: 10.1007/s10409-024-23608-x. [32] REN Q F, ZHANG Y R, HU L L, et al. Achieving synchronous compression-shear loading on SHPB by utilizing mechanical metamaterial [J]. International Journal of Impact Engineering, 2024, 186: 104888. DOI: 10.1016/j.ijimpeng.2024.104888. [33] QIAO D, YANG B, JIANG Z Y, et al. A new plastic flow theoretical model and verification for non-dense metals [J]. Acta Mechanica Sinica, 2023, 39(9): 423085. DOI: 10.1007/s10409-023-23085-x. [34] YE W K, HU L L, OU H F, et al. Mere tension output from spring-linkage-based mechanical metamaterials [J]. Science Advances, 2023, 9(30): 3870. DOI: 10.1126/sciadv.adh3870. [35] YASUDA H, MIYAZAWA Y, CHARALAMPIDIS E G, et al.Origami-based impact mitigation via rarefaction solitary wave creation [J]. Science Advances, 2019, 5(5): 2835. DOI: 10.1126/sciadv.aau2835. -
计量
- 文章访问数: 51
- HTML全文浏览量: 14
- PDF下载量: 13
- 被引次数: 0