Numerical simulation of peak pressure in near-field underwater explosion
-
摘要:
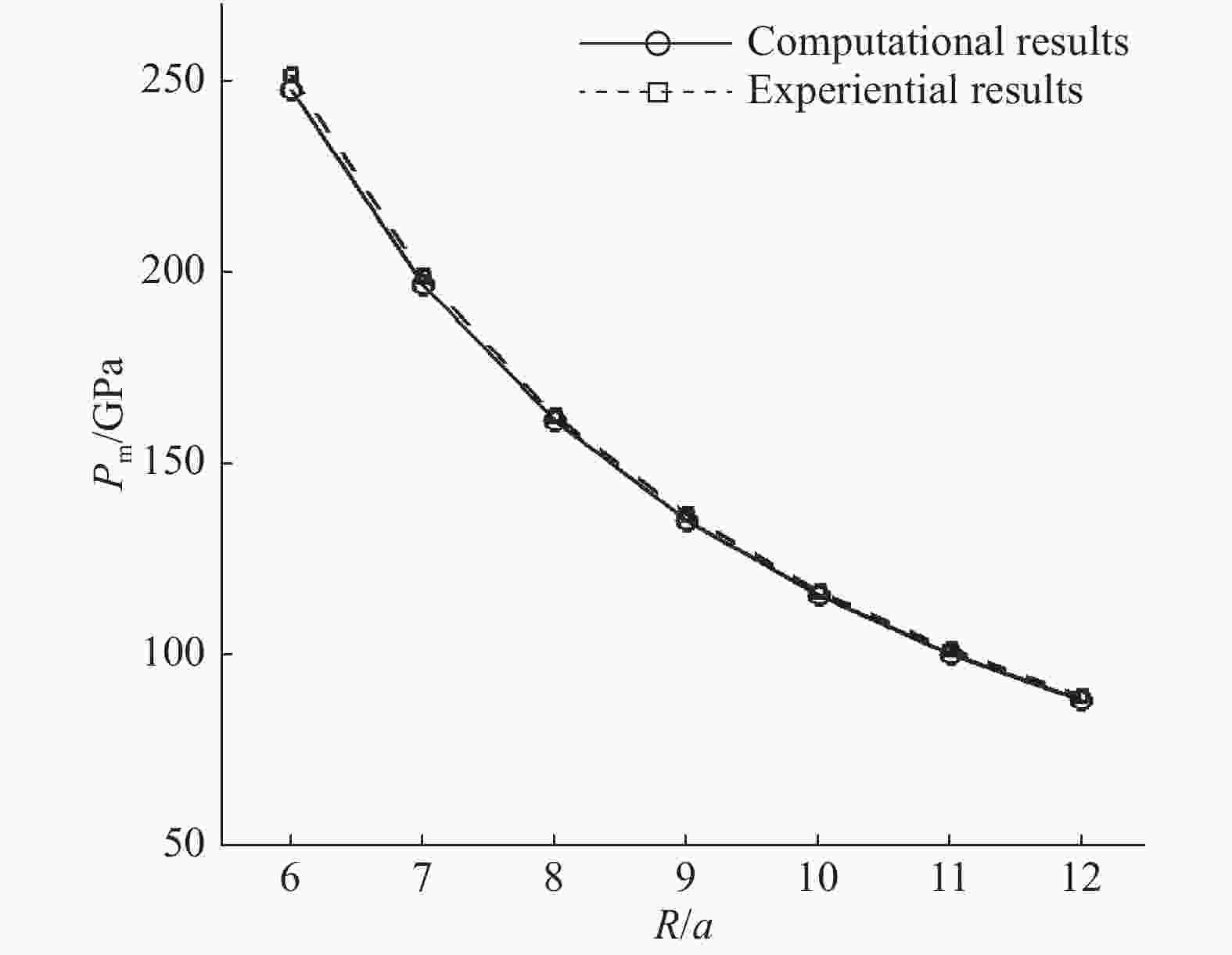
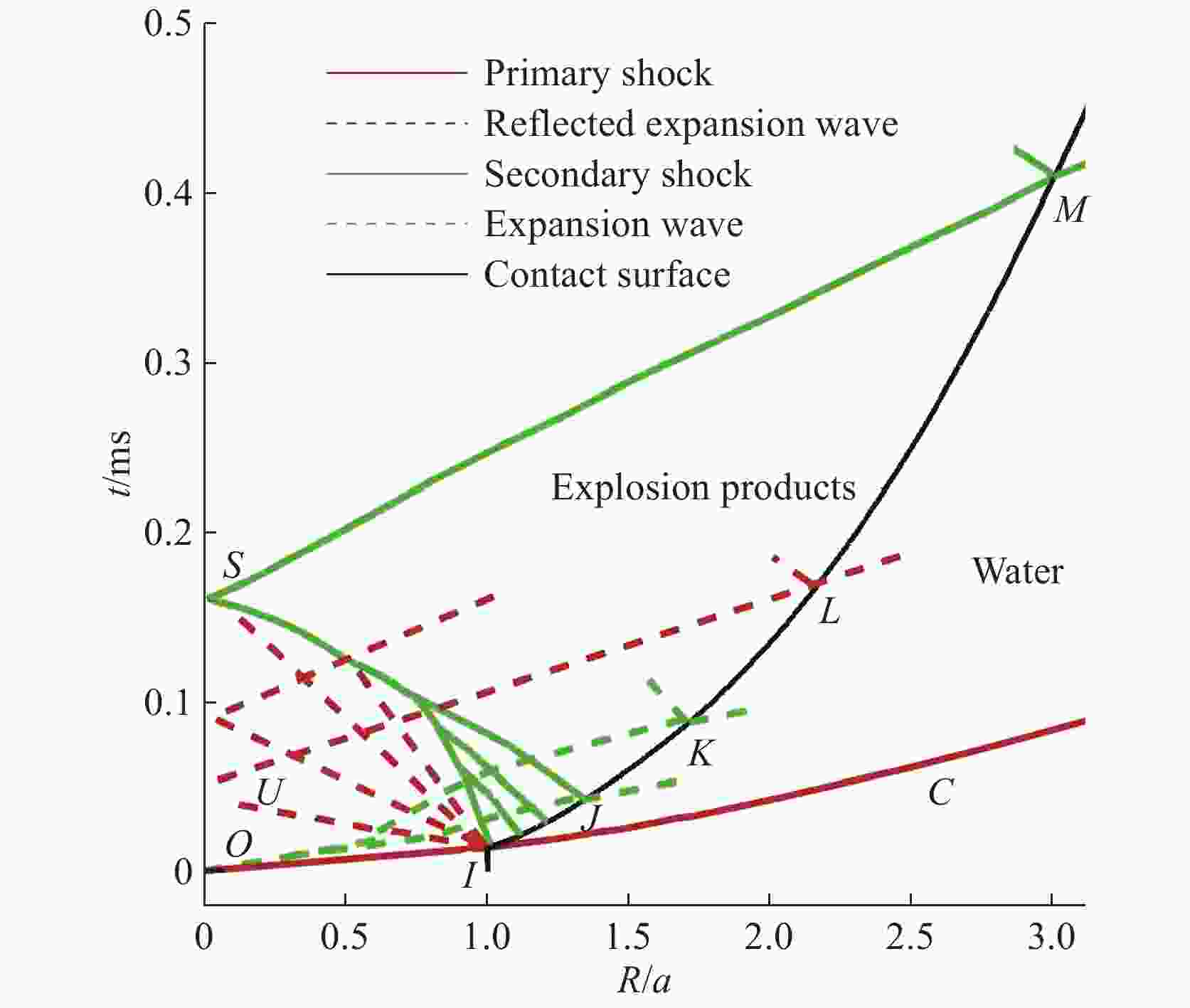
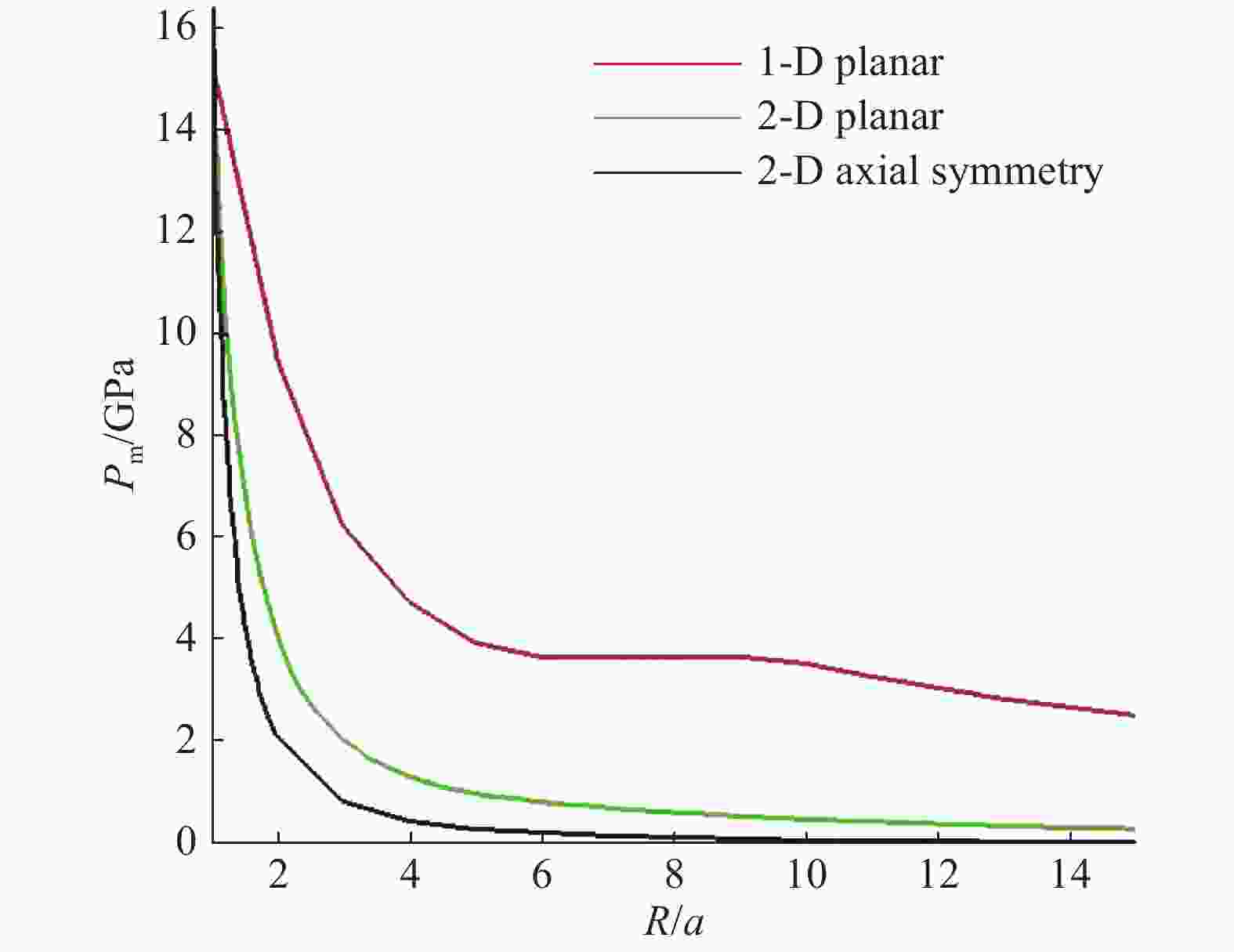
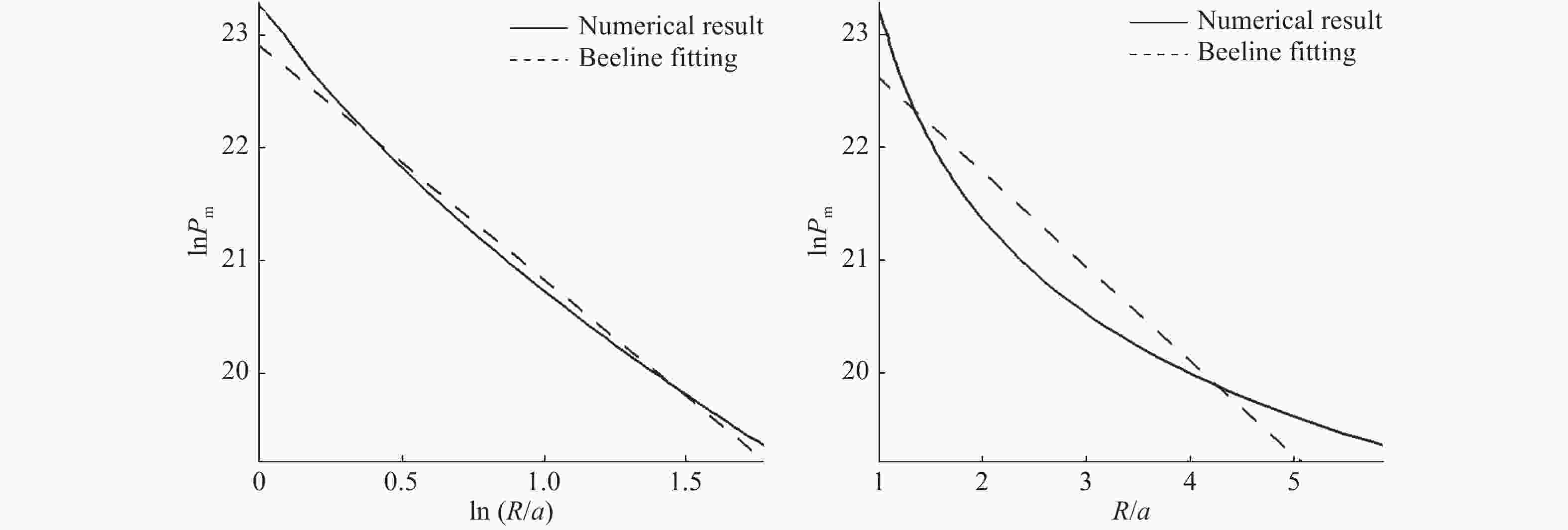
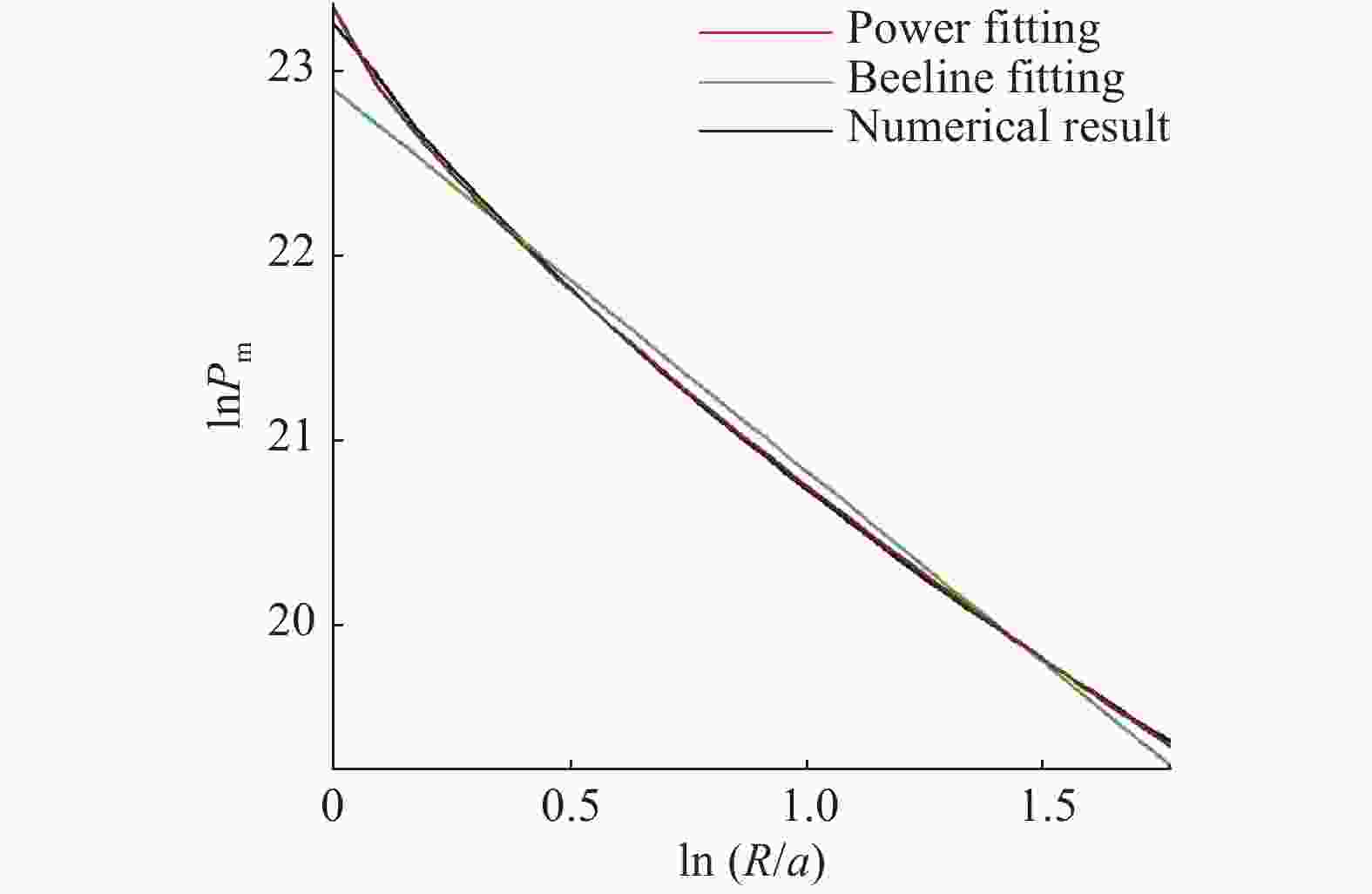
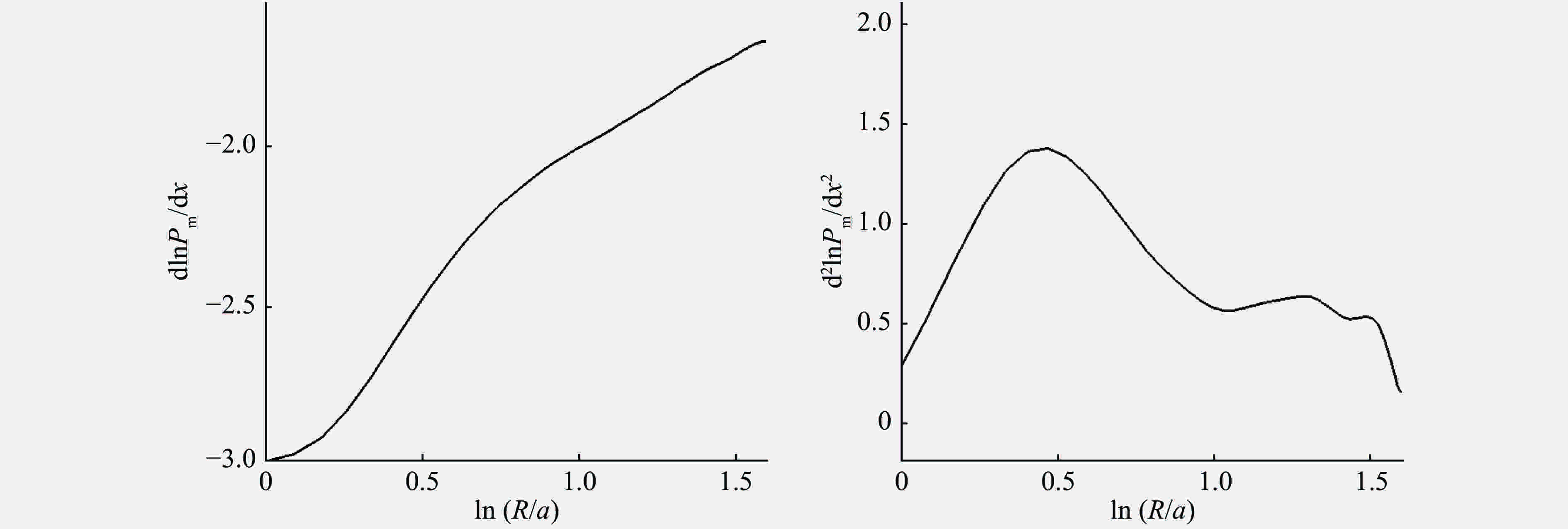
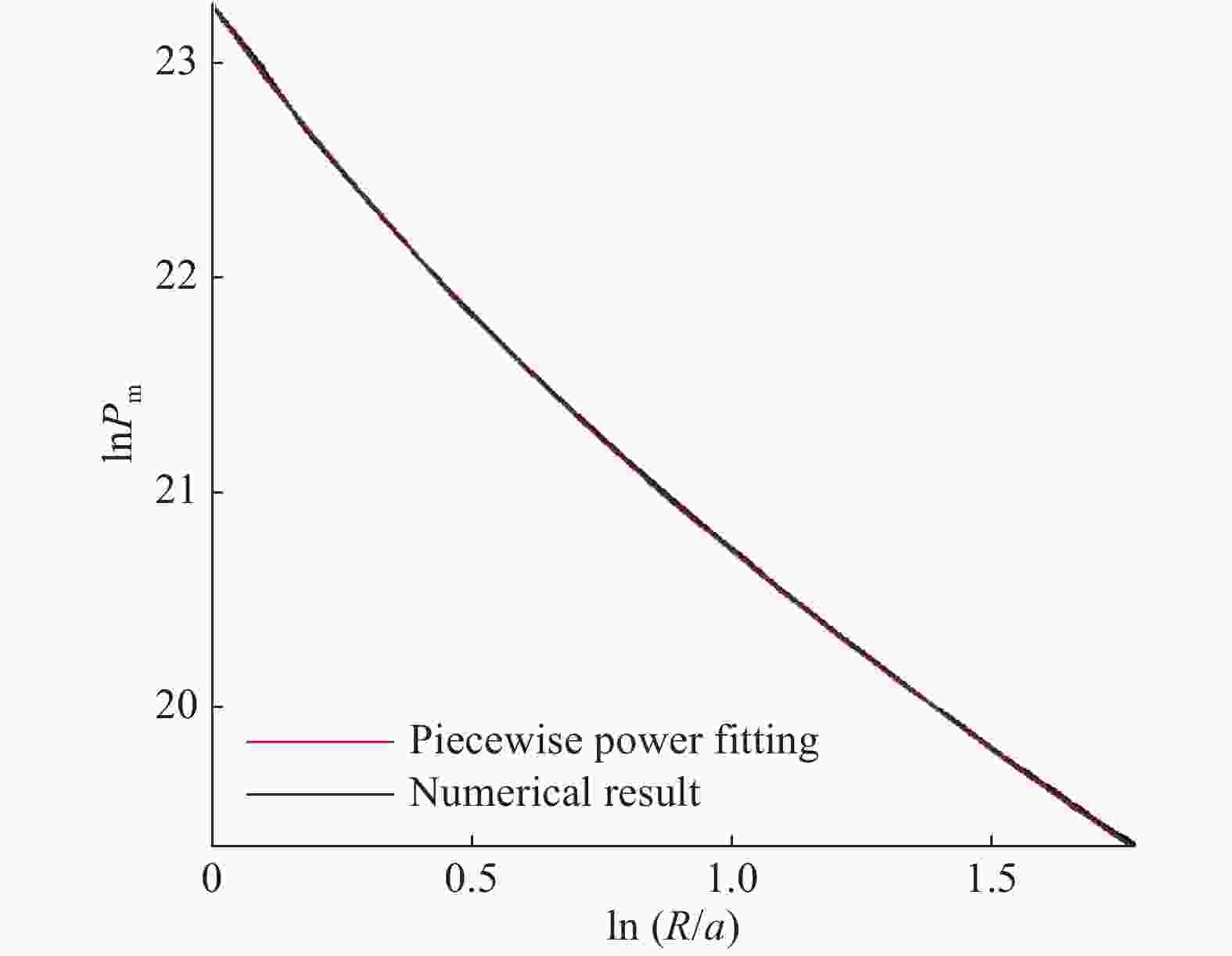
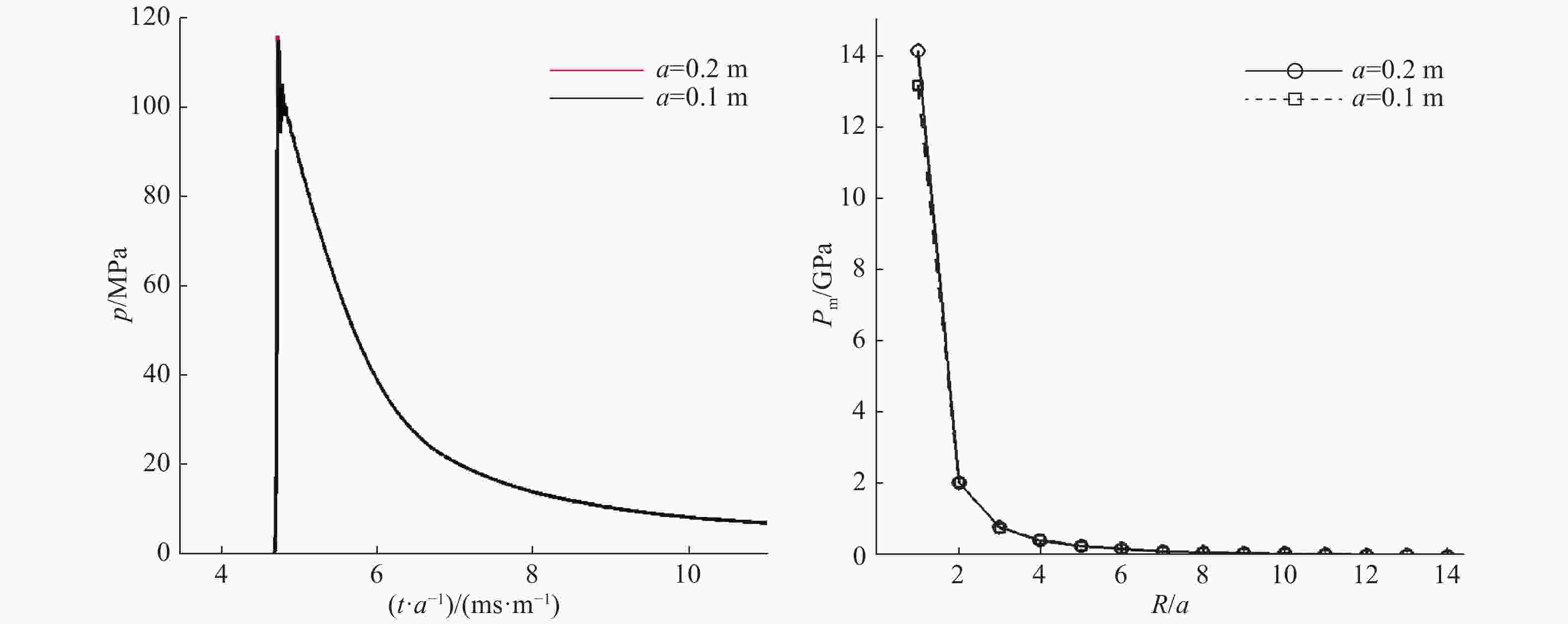
为了研究水下爆炸近场内的压力状态,使用SPH (smoothed particle hydrodynamics)方法,采用C-J爆轰模型,对水下爆炸过程进行了数值模拟。通过与峰值压力规律和中场内经验公式的比较,验证了程序的可靠性。对水下爆炸过程进行了波系分析,与不同维数水下爆炸的数值模拟结果进行了对比研究。结果表明:比距离R/a=6是波形变化的一个分界点,在R/a<6的近场范围内,峰值压力的拟合分为两段更合适。另外,对数值结果的lnPm-ln(R/a)曲线进行了分段幂次拟合,得到了与数值模拟结果非常吻合的拟合曲线。
Abstract:In this work, to obtain the pressure state of underwater explosion in near-field, we numerically simulated the whole process of underwater explosion using the smoothed particle hydrodynamics and adopting the C-J detonation model, and following the empirical formulas, confirmed the laws of the peak pressure, thereby verifying the effectiveness of the numerical program. We also analyzed the waves' propagation in underwater explosion and compared it with the numerical results of underwater explosion in various dimensions. The results show that the distance ratio R/a=6 is a demarcation point in the waves structure, and in the R/a<6 near-field range the fitted peak pressure curve should be divided into two sections. Further, we performed segmented fitting of the numerical results with power function, and found the fitted curve in good agreement with the numerical results.
-
Key words:
- underwater explosion /
- peak pressure /
- near-field /
- smoothed particle hydrodynamics /
- dimension effect /
- power fitting
-
-
[1] 库尔. 水下爆炸[M]. 罗耀杰, 韩润泽, 官信, 等译. 北京: 国防工业出版社, 1960. [2] DORSETT H, CLIFF M D. Detonation front curvature measurements and aquarium tests of tritonal variants: ARML, DSTO-TR-1411 [R]. 2003. [3] BENTEROU J, BENNETT C V, COLE G, et al. Internal detonation velocity measurements inside high Explosives: LLNL-PROC-409969 [R]. 2009. [4] 池家春, 马冰. TNT/RDX(40/60)炸药球水中爆炸波研究 [J]. 高压物理学报, 1999, 13(3): 199–204. DOI: 10.11858/gywlxb.1999.03.008.CHI Jiachun, MA Bing. Underwater explosion wave by a spherical charge of composition B-3 [J]. Chinese Journal of High Pressure Physics, 1999, 13(3): 199–204. DOI: 10.11858/gywlxb.1999.03.008. [5] 赵继波, 谭多望, 李金河, 等. TNT药柱水中爆炸近场压力轴向衰减规律 [J]. 爆炸与冲击, 2008, 28(6): 539–543. DOI: 10.3321/j.issn:1001-1455.2008.06.010.ZHAO Jibo, TAN Duowang, LI Jinhe, et al. Axial pressure damping of cylindrical tnt charges in the near underwater-explosion field [J]. Explosion and Shock Waves, 2008, 28(6): 539–543. DOI: 10.3321/j.issn:1001-1455.2008.06.010. [6] 师华强, 宗智, 贾敬蓓. 水下爆炸冲击波的近场特性 [J]. 爆炸与冲击, 2009, 29(2): 125–130. DOI: 10.3321/j.issn:1001-1455.2008.06.010.SHI Huaqiang, ZONG Zhi, JIA Jingbei. Short-range characters of underwater blast waves [J]. Explosion and Shock Waves, 2009, 29(2): 125–130. DOI: 10.3321/j.issn:1001-1455.2008.06.010. [7] 张远平, 李金河, 龚晏青, 等. 水下爆炸近场冲击波压力测试研究 [J]. 仪器仪表学报, 2009, 30(6): 58–61.ZHANG Yuanping, LI Jinhe, GONG Yanqing, et al. Measuring study on shock wave pressure at near-field during underwater explosion [J]. Chinese Journal of Scientific Instrument, 2009, 30(6): 58–61. [8] 李晓杰, 李现远, 张程娇, 等. 水下爆炸近场冲击波速度连续测试 [C] // 中国力学大会, 2013.LI Xiaojie, LI Xianyuan, ZHANG Chengjiao, et al. Continuous velocity measurement of underwater explosion shock wave in the near field [C] // The Chinese Congress of Theoretical and Applied Mechanics(CCTAM2013), 2013. [9] LIU G R, LIU M B. Smoothed particle hydrodynamics: a meshfree particle method [M]. translated by HAN Xu, YANG Gang, QIANG Hongfu, et al. Changsha: Hunan University Press, 2005. [10] ZHANG Aman, YANG Wenshan, HUANG Chao, et al. Numerical simulation of column charge underwater explosion based on SPH and BEM combination [J]. Computers & Fluids, 2013(7): 169–178. DOI: 10.1016/j.compfluid.2012.10.012. [11] BROOKSHAW L. Smooth particle hydrodynamics in cylindrical coordinates [J]. Australian and New Zealand Industrial and Applied Mathematics Journal, 2003, 44(E): C114–C139. DOI: 10.21914/anziamj.v44i0.675. [12] 李维新. 一维不定常流与冲击波[M]. 北京: 国防工业出版社, 2003. [13] 李晓杰, 张程娇, 王小红, 等. 水的状态方程对水下爆炸影响的研究 [J]. 工程力学, 2014, 31(8): 46–52. DOI: 10.6052/j.issn.1000-4750.2013.03.0180.LI Xiaojie, ZHANG Chengjiao, WANG Xiaohong, et al. Numerical study on the effect of equations of state of water on underwater explosions [J]. Engineering Mechanics, 2014, 31(8): 46–52. DOI: 10.6052/j.issn.1000-4750.2013.03.0180. [14] ZAMYSHLYAYEV B V, YAKOVLEV Y S. Dynamic loads in underwater explosion[M]. Washington, D. C. AD-757183,1973. -






 下载:
下载: