Reliability analysis and design optimization of a shear pin constrained by mechanical boundaries
-
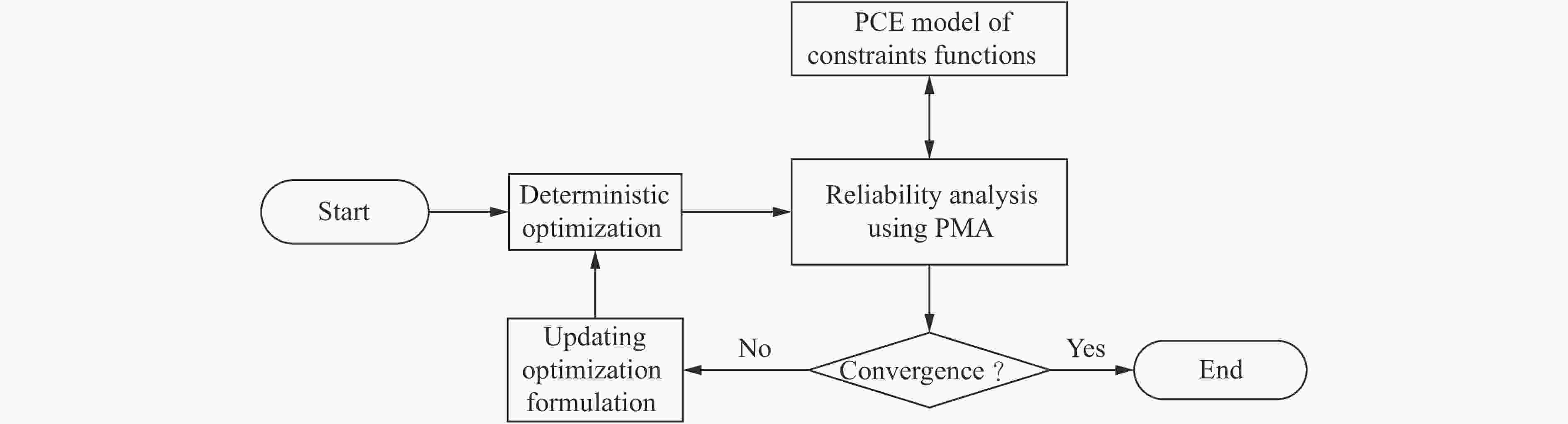
摘要: 剪切销是火工装置关键部件,其可靠性不仅表现为点火作用下可靠剪断,还表现为受力学环境激励不发生断裂。本文中以多项式混沌展开方法为基础,建立了力学环境约束下的剪切销分析模型,结合序贯优化与可靠性分析方法,提出了剪切销可靠性优化设计的思路。以某型火工作动装置为应用实例,依据实用的力学环境,进行了剪切销可靠性分析及优化设计,揭示了设计参数与力学环境之间的关系,并获得了影响可靠性的关键参数。最后,开展了优化后的火工作动装置实验测试,结果佐证了优化设计的有效性。Abstract: The shear pin is a key component of an explosive-actuated device. It must be cut by explosive force and guarantee regular work under mechanical environment in reliability analysis. The mechanical model of the shear pin constrained by the mechanical boundary is built based on the polynomial chaos expansion (PCE) method. Then, the sequential optimization and reliability assessment (SORA) method is adopted to promote a reliability-based design optimization (RBDO) for the shear pin. An explosive-actuated device is selected as an application example of reliability analysis and design, which is based on the idea proposed in this paper. Through the parametric sensitivity analysis of the shear pin, the relationship between designing parameters and mechanical environments is revealed and the effective factors on its reliability are obtained. At last, the explosive-actuated device is manufactured with optimal parameters and works normally under mechanical environment. It is proved that the promoted idea is accurate and useful for the reliability design and optimization of the shear pin under mechanical environments.
-
表 1 火工作动装置工作环境
Table 1. Work situation of the pyrotechnic pin
表 2 影响火工作动装置可靠性的因素
Table 2. Influence factors on the pyrotechnic pin reliability
序号 参数符号 参数名称 参数均值 参数标准差 1 ppow 火药工作产生压强 10 MPa 2.5 MPa 2 S1 火药压力作用面积 500 mm2 5 mm2 3 d 剪切销截面直径 2.5 mm 0.1 mm 4 E 7075铝合金弹性模量 70 GPa 0.005 GPa 5 σb 7075铝合金极限强度 429 MPa 5 MPa 6 σfatigue 7075铝合金真实断裂强度 627 MPa 5 MPa 7 εfatigue 7075铝合金真实断裂延性 0.29 0.000 5 8 μ 泊松比 0.33 0.000 5 9 l 剪切面长度 3.5 mm 0.1 mm 10 ξ 损耗因子 0.005 0.001 11 mcylinderpin 圆柱销质量 15 g 0.1 g 12 acylinderpin 圆柱销加速度 200 m/s2 10 m/s2 13 tvib 振动时长 10 h 1 h 14 σmean 平均预紧力 400 MPa 5 MPa 15 aimpact 起落冲击(发射冲击)加速度幅值 200(30 000) m/s2 100 m/s2 16 timpact 起落冲击(发射冲击)时长 11(3) ms 1 ms 表 3 变量对不同工作环境的不确定性灵敏度
Table 3. Uncertainty sensitivity of variables in different mechanic environments
参数 点火工作 产品发射 载机加速 载机起落 挂载飞行 综合影响系数 τ1 σ1 σ2 τ2 τ3 σ3 σ4 τ4 σ5 ppow 0.260 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.029 S1 0.302 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.034 d 0.289 0.226 0.199 0.178 0.378 0.233 0.236 0.258 0.254 0.250 E 0.000 0.106 0.092 0.128 0.000 0.110 0.064 0.072 0.063 0.070 σb 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.062 0.007 σfatigue 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.046 0.005 εfatigue 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.057 0.006 μ 0.000 0.000 0.000 0.107 0.000 0.000 0.000 0.071 0.000 0.020 l 0.000 0.000 0.126 0.099 0.000 0.000 0.135 0.043 0.000 0.045 ξ 0.000 0.019 0.012 0.010 0.000 0.016 0.019 0.017 0.034 0.014 mcylinderpin 0.000 0.112 0.115 0.090 0.202 0.121 0.065 0.065 0.060 0.092 acylinderpin 0.000 0.000 0.000 0.000 0.203 0.000 0.000 0.000 0.000 0.023 tvib 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.121 0.014 σmean 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.136 0.015 aimpact 0.000 0.173 0.156 0.130 0.000 0.158 0.173 0.159 0.000 0.106 timpact 0.000 0.197 0.157 0.133 0.000 0.178 0.152 0.141 0.000 0.107 注:τ1、τ2、τ3、τ4为剪切应力,σ1、σ3为弯曲应力,σ2、σ4为拉伸应力,σ5为疲劳破坏应力。 表 4 设计变量初值、取值范围和优化值
Table 4. Initial values, ranges and optimal values of design variables
设计变量 单位 初值 优化值 取值范围 ppow MPa 10.00 13.51 [8, 15] d mm 2.50 1.49 [1, 2] l mm 3.50 2.62 [1, 3] σmean MPa 400 300 [300, 400] -
[1] 荣吉利, 宋乾强, 张涛. 一种预测航天火工装置可靠性的小样本方法 [J]. 宇航学报, 2015, 36(3): 360–364. DOI: 10.3873/j.issn.1000-1328.2015.03.016.RONG Jili, SONG Qianqiang, ZHANG Tao. A small sample method for predicting reliability of space pyrotechnic devices [J]. Journal of Astronautics, 2015, 36(3): 360–364. DOI: 10.3873/j.issn.1000-1328.2015.03.016. [2] 荣吉利, 宋乾强, 张涛, 等. 冗余航天火工装置可靠性评估方法及应用 [J]. 宇航学报, 2013, 34(7): 1021–1026. DOI: 10.3873/j.issn.1000-1328.2013.07.019.RONG Jili, SONG Qianqiang, ZHANG Tao. Reliability assessment method for redundant aerospace pyrotechnic devices and its application [J]. Journal of Astronautics, 2013, 34(7): 1021–1026. DOI: 10.3873/j.issn.1000-1328.2013.07.019. [3] 董海平, 蔡瑞娇, 穆慧娜. 火工品可靠性计量计数评估方法的有效性研究 [J]. 含能材料, 2008, 16(5): 553–555. DOI: 10.3969/j.issn.1006-9941.2008.05.020.DONG Haiping, CAI Ruijiao, MU Huina. Validity of variables attributes assessment method for reliability of initiating explosive devices [J]. Chinese Journal of Energetic Materials, 2008, 16(5): 553–555. DOI: 10.3969/j.issn.1006-9941.2008.05.020. [4] 董海平, 赵霞, 蔡瑞娇. 基于信息等值的火工品可靠性评估小样本方法 [J]. 兵工学报, 2011, 32(5): 554–558.DONG Haiping, ZHAO Xia, CAI Ruijiao. An assessment method of reliability of initiating devices based on information measure equivalency [J]. Acta Armamentarii, 2011, 32(5): 554–558. [5] 董海平, 蔡瑞娇, 穆慧娜, 等. 火工品可靠性的感度参数设计法 [J]. 爆炸与冲击, 2009, 29(6): 613–616. DOI: 10.11883/1001-1455(2009)06-0613-04 .DONG Haiping, CAI Ruijiao, MU Huina, et al. A sensitivity parameter design method for reliability of explosive initiators [J]. Explosion and Shock Waves, 2009, 29(6): 613–616. DOI: 10.11883/1001-1455(2009)06-0613-04 . [6] 伊枭剑, 董海平, 翟志强, 等. 基于应力-强度干涉模型的火工品可靠性设计方法 [J]. 北京理工大学学报, 2014, 34(10): 1007–1011.YI Xiaojian, DONG Haiping, ZHAI Zhiqiang, et al. Reliability design for initiating devices based on stress-strength interference model [J]. Transactions of Beijing Institute of Technology, 2014, 34(10): 1007–1011. [7] OUCH R, UKRITCHON B, PIPATPONGSA T, et al. Finite element analyses of the stability of a soil block reinforced by shear pins [J]. Geomechanics and Engineering, 2017, 12(6): 1021–1046. [8] 孙洁, 郭崇星, 吴瑞德, 等. 拔销器作用过程的仿真研究 [J]. 火工品, 2017(1): 10–13. doi: 10.3969/j.issn.1003-1480.2017.01.004SUN Jie, GUO Chongxing, WU Ruide, et al. Simulation research on the function process of the pin puller [J]. Initiators and Pyrotechnics, 2017(1): 10–13. doi: 10.3969/j.issn.1003-1480.2017.01.004 [9] 高滨. 火工作动装置设计参数的敏感性分析 [J]. 航天返回与遥感, 2006, 27(3): 57–60. doi: 10.3969/j.issn.1009-8518.2006.03.011GAO Bin. Design parameter sensitivity analysis of pyrotechnically actuated devices [J]. Space Craft Recovery and Remote Sensing, 2006, 27(3): 57–60. doi: 10.3969/j.issn.1009-8518.2006.03.011 [10] COLANTUONO T, GROSSONI I, ALLEN P, et al. The optimal strength of shear pins: requirements in point run-throughs [J]. Journal of Rail and Rapid Transit, 2016, 232(2): 2–19. DOI: 10.1177/0954409716682657. [11] SALTELLI A, RATTO M, ANDRES T, et al. Global sensitivity analysis: the primer [M]. Chichester: John Wiley and Sons, 2008. [12] HELTON J C, JOHNSON J D, SALLABERRY C J, et al. Survey of sampling-based methods for uncertainty and sensitivity analysis [J]. Reliability Engineering and System Safety, 2006, 91(10/11): 1175–1209. [13] IMAN R L, HELTON J C. An investigation of uncertainty and sensitivity analysis techniques for computer models [J]. Risk Analysis, 2010, 8(1): 71–90. [14] WIENER N. The homogeneous chaos [J]. American Journal of Mathematics, 1938, 60(4): 897–936. doi: 10.2307/2371268 [15] DU Xiaoping, GUO Jia, BEERAM H. Sequential optimization and reliability assessment for multidisciplinary systems design [J]. Structural and Multidisciplinary Optimization, 2008, 35(2): 117–130. DOI: 10.1007/s00158-007-0121-7. [16] 崔卫东, 关云翔, 惠蕾. 拔销器的小型化设计 [J]. 火工品, 2006(2): 17–19. doi: 10.3969/j.issn.1003-1480.2006.02.005CUI Weidong, GUAN Yunxiang, HUI Lei. Design of the small-sized piston actuator [J]. Initiators and Pyrotechnics, 2006(2): 17–19. doi: 10.3969/j.issn.1003-1480.2006.02.005 [17] 汪凤泉. 电子设备振动与冲击手册 [M]. 北京: 科学出版社, 1998. [18] 苟文选. 材料力学 [M]. 北京: 科学出版社, 2005. [19] 徐鹏. 金属材料应变寿命曲线估算的新方法[D]. 南京: 南京航空航天大学, 2012.XU Peng. A new method for the estimation of strain-life curve of metals [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012. [20] 陈小前, 姚雯, 欧阳琦. 飞行器不确定性多学科设计优化理论与应用 [M]. 北京: 科学出版社, 2013. [21] 王若冰, 谷良贤, 龚春林. 随机-区间混合不确定性分层序列化多学科可靠性分析方法 [J]. 西北工业大学学报, 2016(1): 139–146. DOI: 10.3969/j.issn.1000-2758.2016.01.021.WANG Ruobing, GU Liangxian, GONG Chunlin. A stratified sequencing multi-disciplinary reliability analysis method under random and interval uncertainty [J]. Journal of Northwestern Polytechnical University, 2016(1): 139–146. DOI: 10.3969/j.issn.1000-2758.2016.01.021. [22] 施荣明、朱广荣、吴飒, 等. 军用装备实验室环境试验方法: 第16部分: 振动试验: GJB 150. 16A-2009 [S]. 北京: 总装备部军标出版发行部, 2009: 42; 53. -






 下载:
下载:



