Numerical study of non-uniformity effect on Richtmyer-Meshkov instability induced by non-planar shock wave
-
摘要:
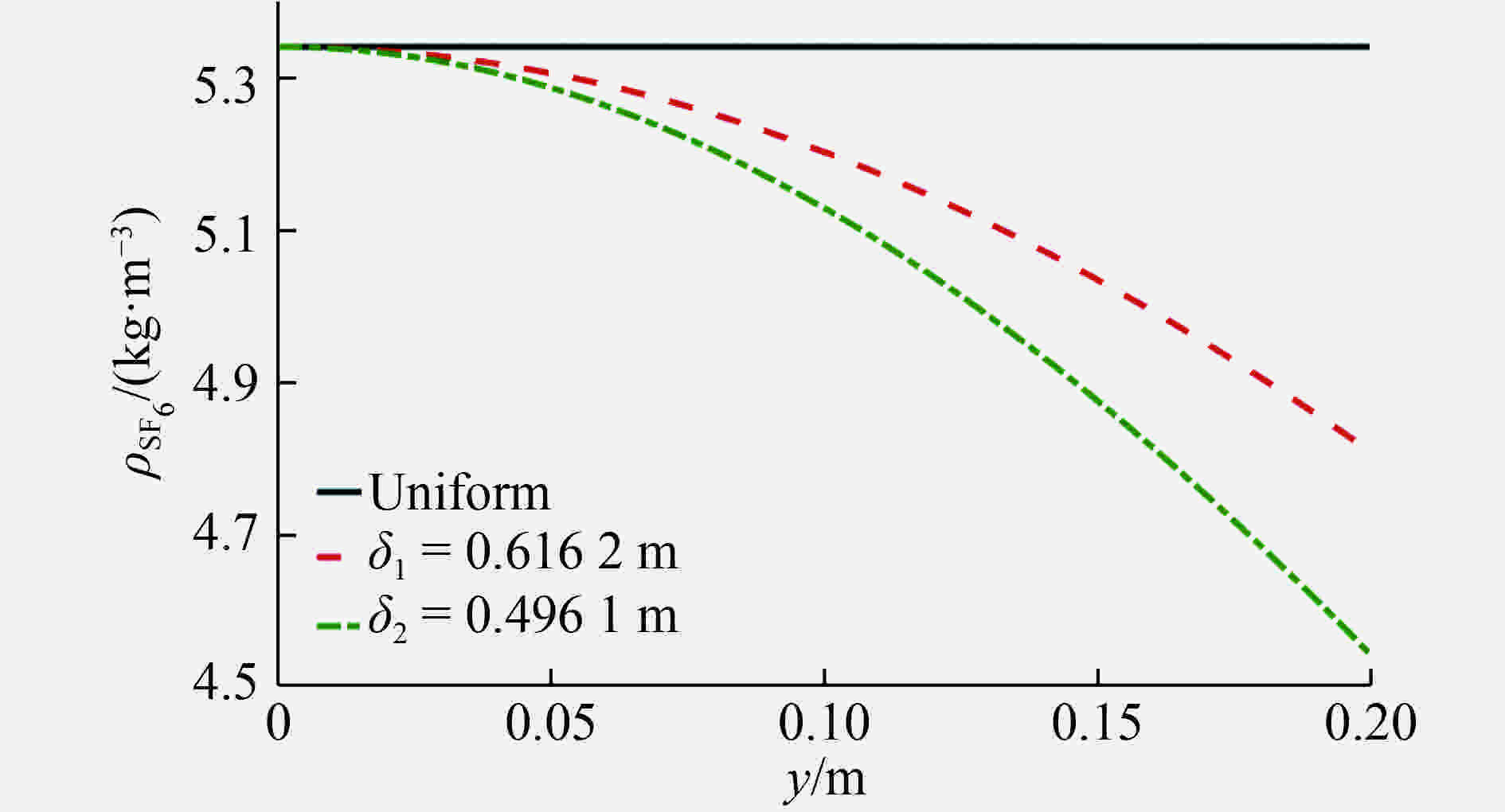
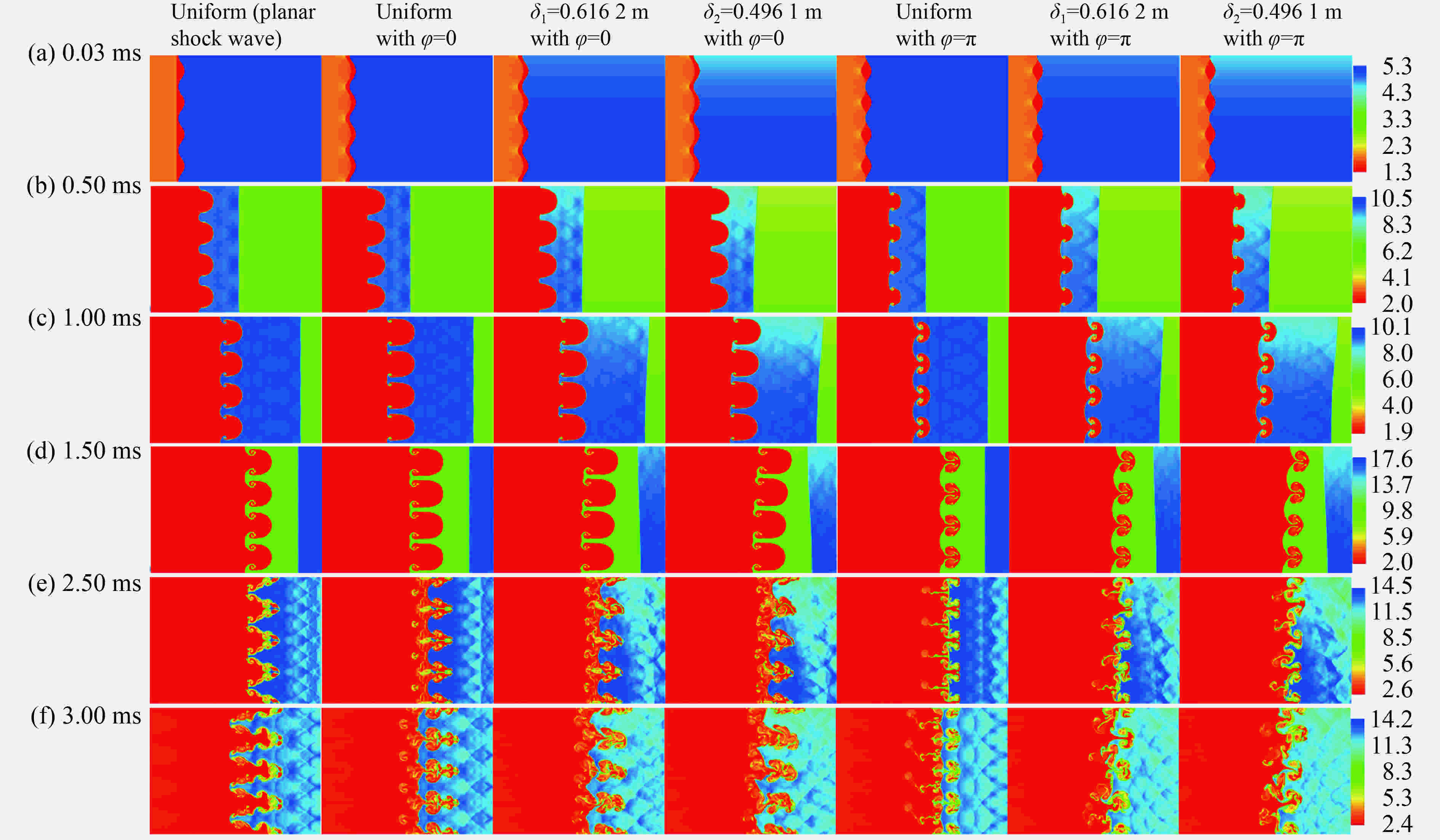
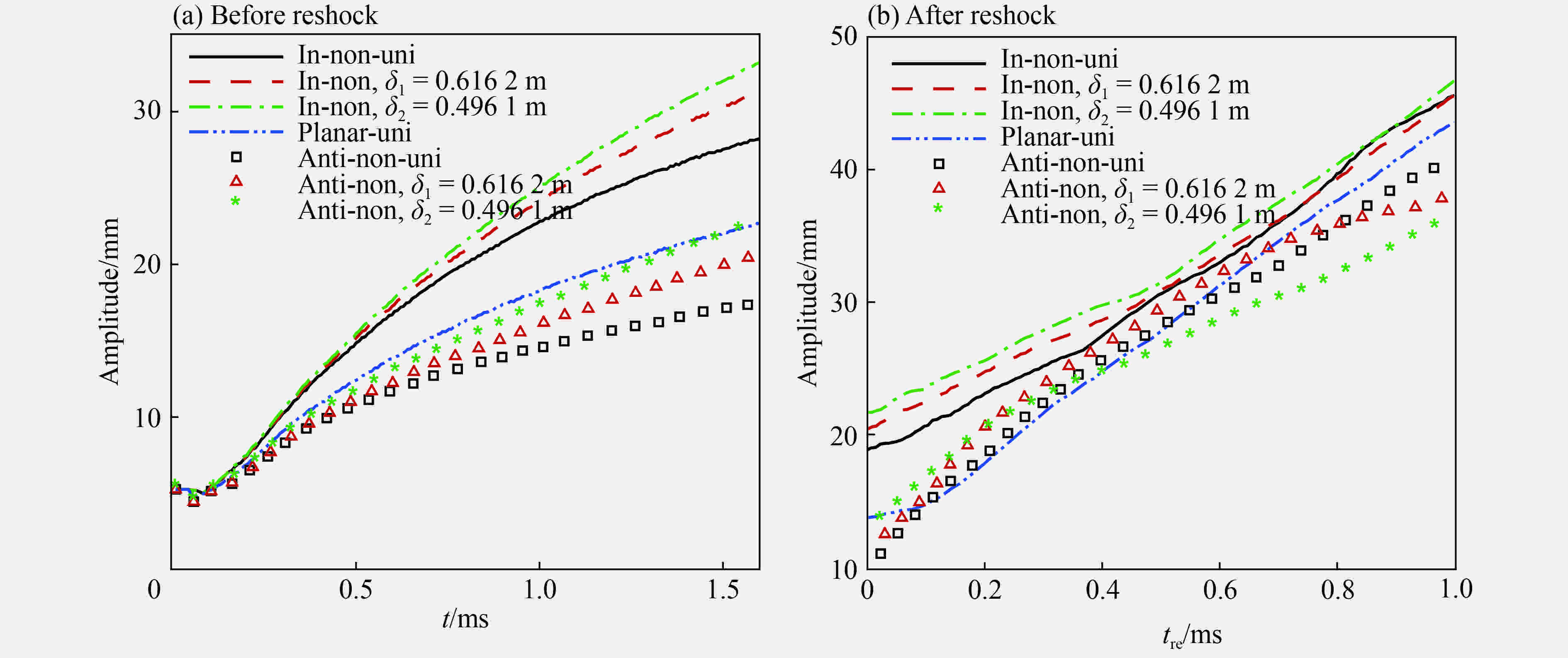
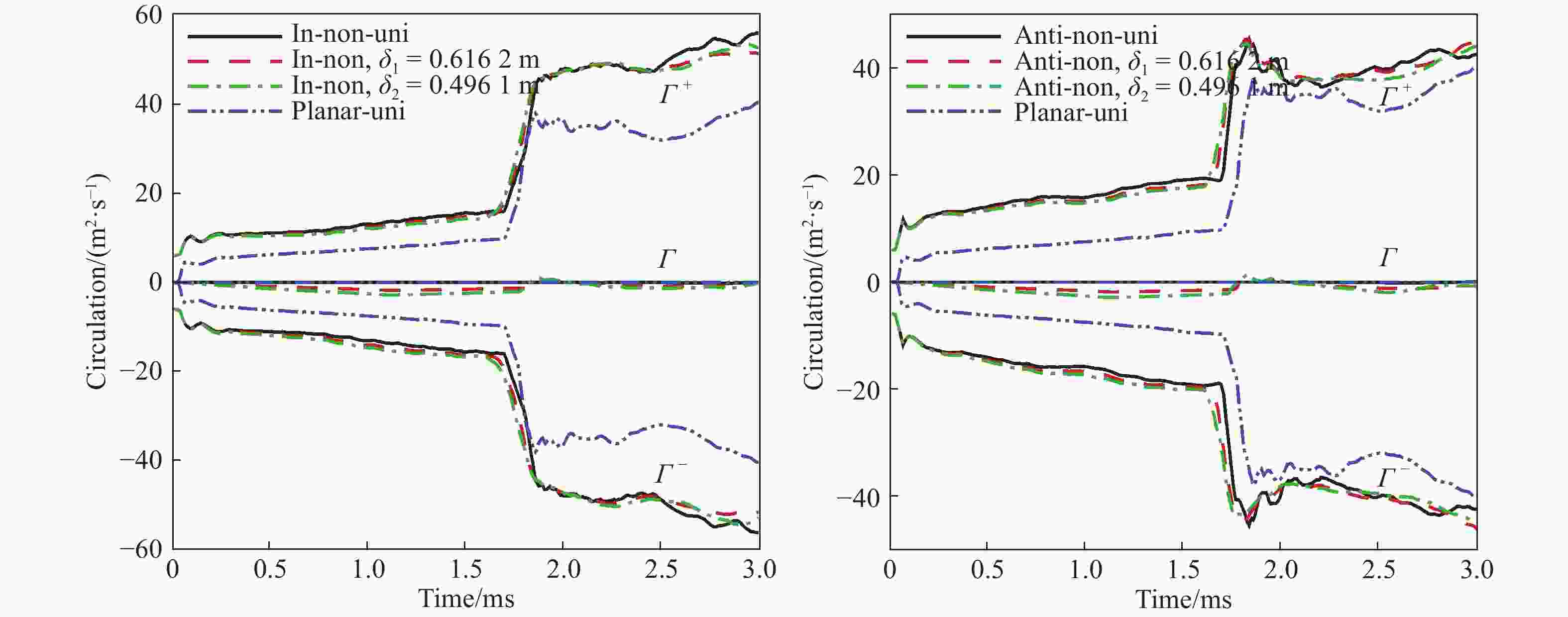
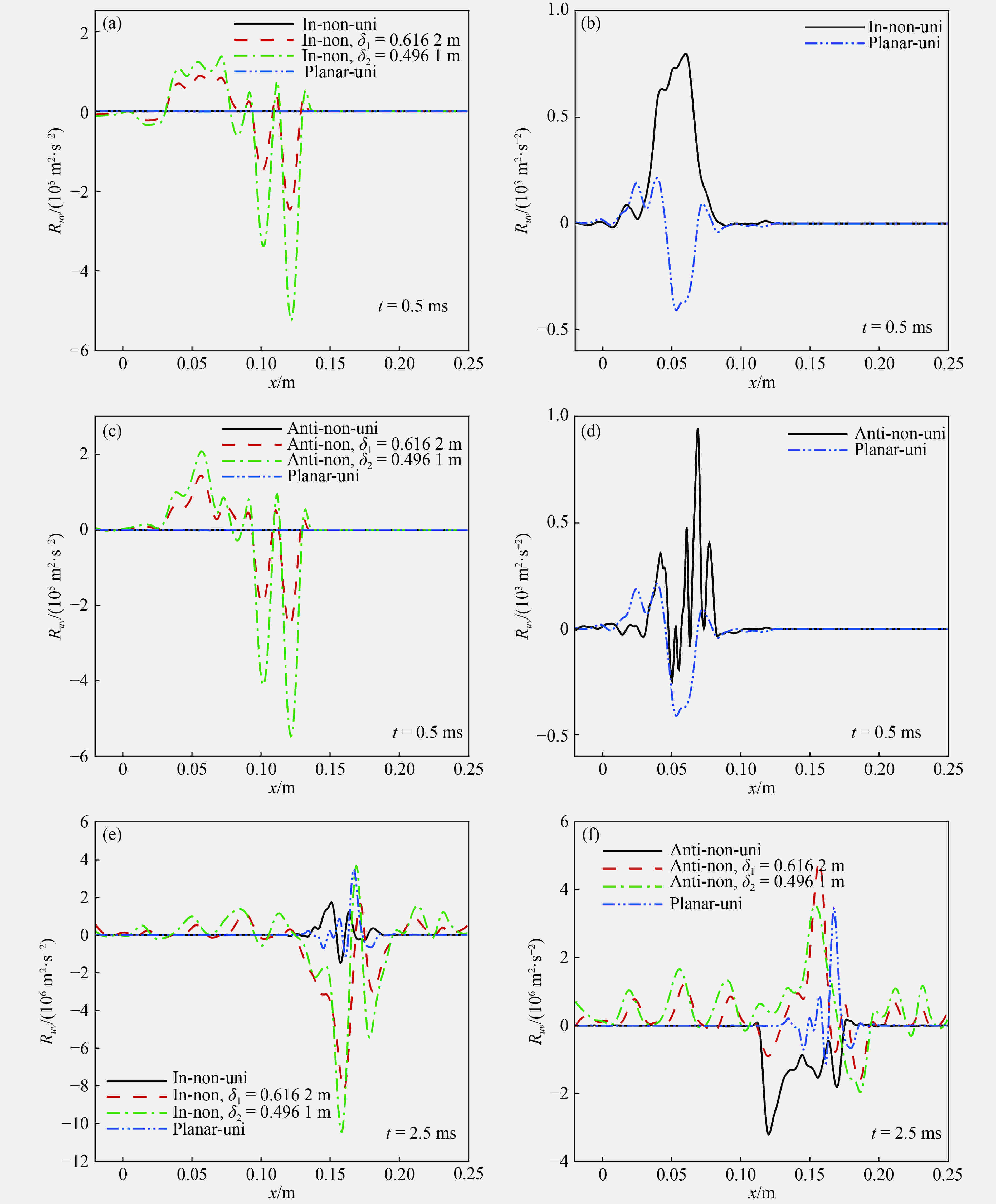
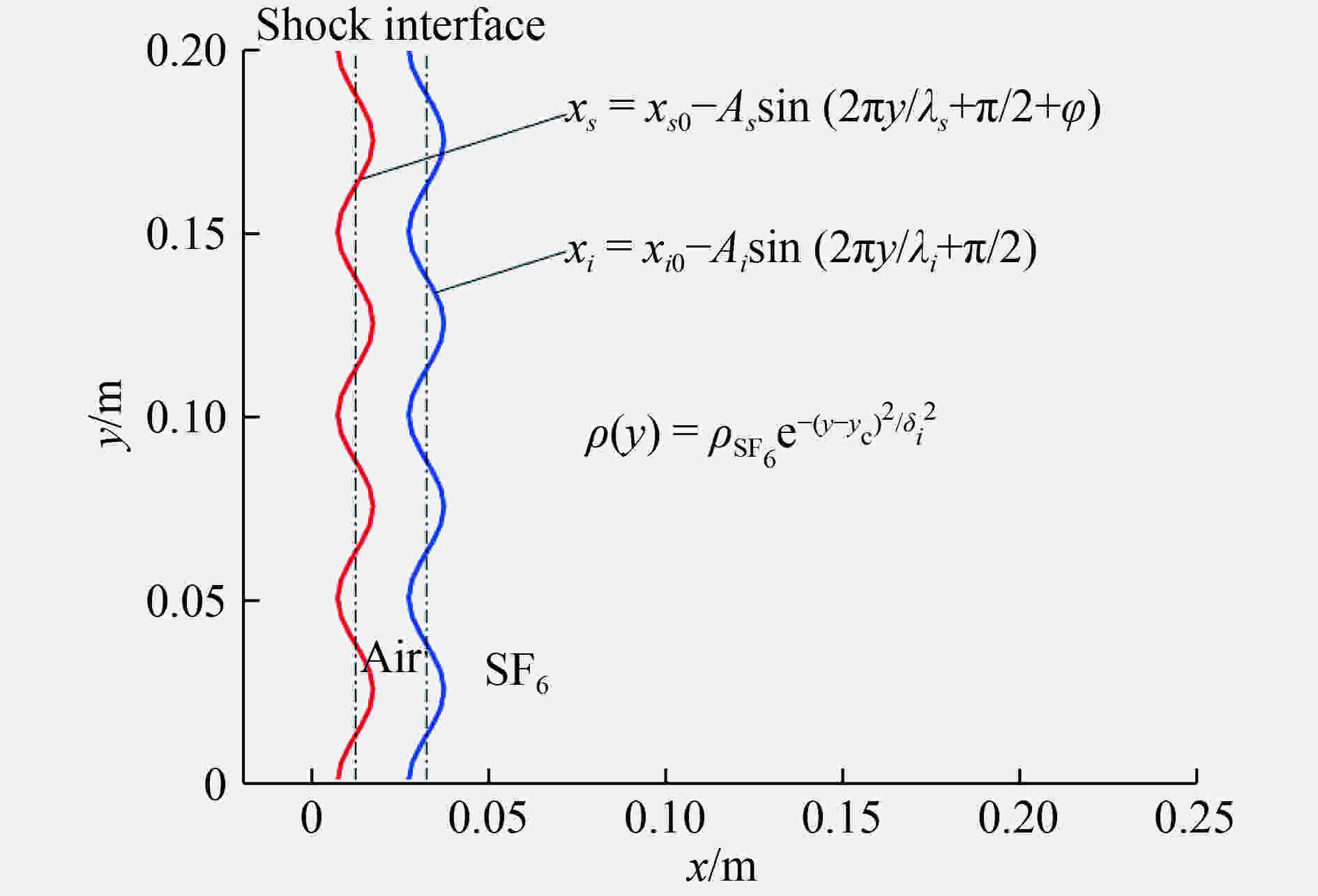
基于Navier-Stokes方程组,采用可压缩多介质黏性流动和湍流大涡模拟程序MVFT (multi-viscous-flow and turbulence),模拟了均匀流场与初始密度呈现高斯函数分布的非均匀流场中马赫数为1.25的非平面激波加载初始扰动air/SF6界面的Richtmyer-Meshkov (RM)不稳定性现象。数值模拟结果表明,初始流场非均匀性将会影响非平面激波诱导的RM不稳定性演化过程。反射激波加载前,非平面激波导致的界面扰动振幅随着流场非均匀性增强而增大;反射激波加载后,非均匀流场与均匀流场条件下的界面扰动振幅差异有所减小。进一步,定量分析流场中环量分布及脉动速度统计量揭示了前述规律的原因。此外,还与平面激波诱导的RM不稳定性进行了简单对比,发现由于非平面激波波阵面区域的涡量与激波冲击界面时产生的涡量的共同作用,使得非平面激波与平面激波诱导的界面失稳过程存在差异。
-
关键词:
- Richtmyer-Meshkov不稳定性 /
- 非均匀流场 /
- 非平面激波 /
- 大涡模拟
Abstract:Based on the Navier-Stokes equations, the large-eddy simulation code MVFT (multi-viscous-flow and turbulence) was applied to numerically study the Richtmyer-Meshkov instability (i.e. RMI) for a perturbed interface, which is driven by a non-planar shock wave with Ma=1.25 in uniform and non-uniform flows with Gaussian distribution of the initial density. The simulation results show that the interface evolution of the RMI induced by non-planar shock wave is affected by the non-uniformity of the initial flows. Before reshock, the growth of the disturbed interface increases with the increasing of the non-uniformity flow field for either φ=0 or φ=π. However, these discrepancies are reduced as the flow enters the turbulent mixing. Further quantitative analysis of the circulations and high-order fluctuating velocity correlation in the flow field reveal the mechanisms for the aforementioned regulations. In addition, it is found that the interface evolution of the RMI induced by non-planar shock wave is different from that driven by planar shock wave. The mechanism for the difference is the influence of the initial vorticity of non-planar shock wave and the vorticity generated by the shock-interface.
-
表 1 Air/SF6初始参数(20 ℃, 101.325 kPa)
Table 1. Properties of air and SF6 gases
Gas ρ/(kg·m−3) γ νl/(mm2·s−1) Prl D/(mm2·s−1) SF6 5.34 1.09 2.47 0.90 9.7 Air 1.29 1.40 15.7 0.71 20.4 表 2 正、负环量相对差值极大值
Table 2. Maximum values of relative difference for positive and negative circulations
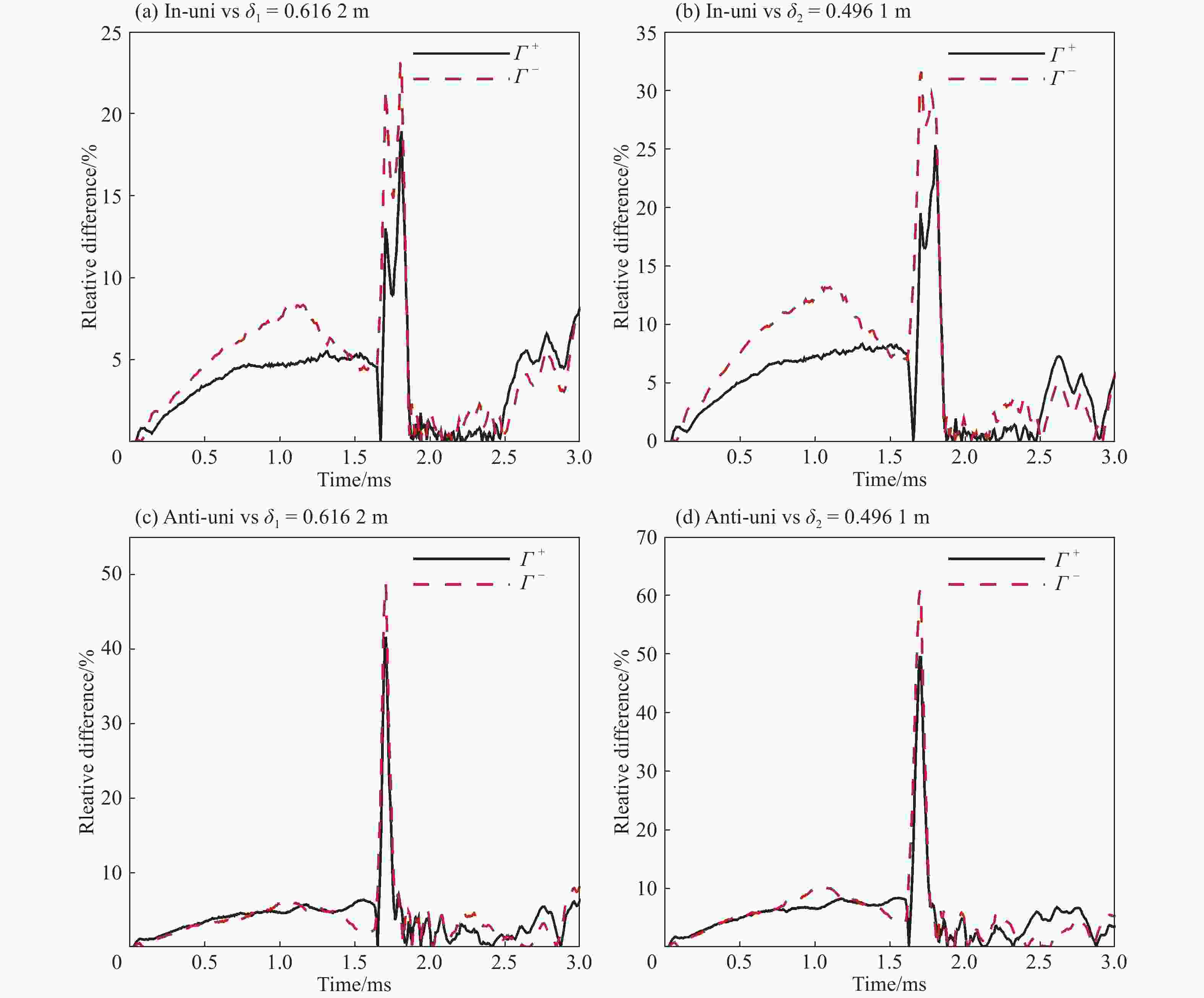
φ Case Relative difference/% Before reshock Transition After reshock Γ + Γ − Γ + Γ − Γ + Γ − 0 Uni vs δ1=0.616 2 m 5.5 8.2 18.6 23.1 7.7 7.6 Uni vs δ2=0.496 1 m 8.3 13.1 25.0 31.4 7.3 5.1 π Uni vs δ1=0.616 2 m 5.7 6.1 40.1 46.9 6.0 7.8 Uni vs δ2=0.496 1 m 8.2 10.2 49.5 60.7 6.7 4.9 -
[1] RICHTMYER R D. Taylor instability in shock acceleration of compressible fluids [J]. Communications on Pure and Applied Mathematics, 1960, 13(2): 297–319. DOI: 10.1002/cpa.3160130207. [2] ARNETT D. The role of mixing in astrophysics [J]. The Astrophysical Journal Supplement Series, 2000, 127(2): 213–217. DOI: 10.1086/313364. [3] YANG J, KUBOTA T, ZUKOSKI E E. Applications of shock-induced mixing to supersonic combustion [J]. AIAA Journal, 1993, 31(5): 854–862. DOI: 10.2514/3.11696. [4] AMENDT P, COLVIN J D, TIPTON R E, et al. Indirect-drive noncryogenic double-shell ignition targets for the national ignition facility: Design and analysis [J]. Physics of Plasmas, 2002, 9(5): 2221–2233. DOI: 10.1063/1.1459451. [5] ZOU L Y, LIU C L, TAN D W, et al. On interaction of shock wave with elliptic gas cylinder [J]. Journal of Visualization, 2010, 13(4): 347–353. DOI: 10.1007/s12650-010-0053-y. [6] BAI J S, ZOU L Y, WANG T, et al. Experimental and numerical study of shock-accelerated elliptic heavy gas cylinders [J]. Physical Review E, 2010, 82(2): 056318. DOI: 10.1103/PhysRevE.82.056318. [7] BAI J S, LIU J H, WANG T, et al. Investigation of the Richtmyer-Meshkov instability with double perturbation interface in nonuniform flows [J]. Physical Review E, 2010, 81(2): 056302. DOI: 10.1103/PhysRevE.81.056302. [8] XIAO J X, BAI J S, WANG T. Numerical study of initial perturbation effects on Richtmyer-Meshkov instability in nonuniform flows [J]. Physical Review E, 2016, 94(1): 013112. DOI: 10.1103/PhysRevE.94.013112. [9] 肖佳欣, 柏劲松, 王涛. 密度非均匀流场中冲击加载双模态界面失稳现象的数值模拟 [J]. 高压物理学报, 2018, 32(1): 82–90. DOI: 10.11858/gywlxb.20170501XIAO Jiaxin, BAI Jingsong, WANG Tao. Numerical study of shock wave impacting on the double-mode interface in nonuniform flows [J]. Chinese Journal of High Pressure Physics, 2018, 32(1): 82–90. DOI: 10.11858/gywlxb.20170501 [10] BAI J S, WANG B, WANG T, et al. Numerical simulation of the Richtmyer-Meshkov instability in initially nonuniform flows and mixing with reshock [J]. Physical Review E, 2012, 86(2): 066319. DOI: 10.1103/PhysRevE.86.066319. [11] ISHIZAKI R, NISHIHARA K, SAKAGAMI H, et al. Instability of a contact surface driven by a nonuniform shock wave [J]. Physical Review E, 1996, 53(6): R5592. DOI: 10.1103/PhysRevE.53.R5592. [12] KANE J O, ROBEY H F, REMINGTON B A, et al. Interface imprinting by a rippled shock using an intense laser [J]. Physical Review E, 2001, 63(2): 055401. DOI: 10.1103/PhysRevE.63.055401. [13] ZOU L Y, LIU J H, LIAO S F, et al. Richtmyer-Meshkov instability of a flat interface subjected to a rippled shock wave [J]. Physical Review E, 2017, 95(1): 013107. DOI: 10.1103/PhysRevE.95.013107. [14] ZHAI Z G, LIANG Y, LIU L L, et al. Interaction of rippled shock wave with flat fast-slow interface [J]. Physics of Fluids, 2018, 30(4): 046104. DOI: 10.1063/1.5024774. [15] 柏劲松, 李平, 王涛, 等. 可压缩多介质粘性流体的数值计算 [J]. 爆炸与冲击, 2007, 27(6): 515–521. DOI: 10.11883/1001-1455(2007)06-0515-07BAI Jingsong, LI Ping, WANG Tao, et al. Computation of compressible multi-viscosity-fluid flows [J]. Explosion and Shock Waves, 2007, 27(6): 515–521. DOI: 10.11883/1001-1455(2007)06-0515-07 [16] 王涛, 柏劲松, 李平, 等. 再冲击载荷作用下流动混合的数值模拟 [J]. 爆炸与冲击, 2009, 29(3): 243–248. DOI: 10.11883/1001-1455(2009)03-0243-06WANG Tao, BAI Jingsong, LI Ping, et al. Numerical simulation of flow mixing impacted by reshock [J]. Explosion and Shock Waves, 2009, 29(3): 243–248. DOI: 10.11883/1001-1455(2009)03-0243-06 [17] 柏劲松, 王涛, 邹立勇, 等. 可压缩多介质粘性流体和湍流的大涡模拟 [J]. 爆炸与冲击, 2010, 30(3): 262–268. DOI: 10.11883/1001-1455(2010)03-0262-07BAI Jingsong, WANG Tao, ZOU Liyong, et al. Large eddy simulation for the multi-viscosity-fluid and turbulence [J]. Explosion and Shock Waves, 2010, 30(3): 262–268. DOI: 10.11883/1001-1455(2010)03-0262-07 [18] 王涛, 李平, 柏劲松, 等. 低密度流体界面不稳定性大涡模拟 [J]. 爆炸与冲击, 2013, 33(5): 487–493. DOI: 10.11883/1001-1455(2013)05-0487-07WANG Tao, LI Ping, BAI Jingsong, et al. Large-eddy simulation of interface instability of low-density fluids [J]. Explosion and Shock Waves, 2013, 33(5): 487–493. DOI: 10.11883/1001-1455(2013)05-0487-07 [19] VREMAN A W. An eddy-viscosity subgrid-scale model for turbulent shear flow: Algebraic theory and applications [J]. Physics of Fluids, 2004, 16(10): 3670–3681. DOI: 10.1063/1.1785131. [20] BAI J S, WANG T, LI P, et al. Numerical simulation of the hydrodynamic instability experiments and flow mixing [J]. Science in China Series G: Physics, Mechanics & Astronomy, 2009, 52(12): 2027–2040. DOI: 10.1007/s11433-009-0277-9. -






 下载:
下载: