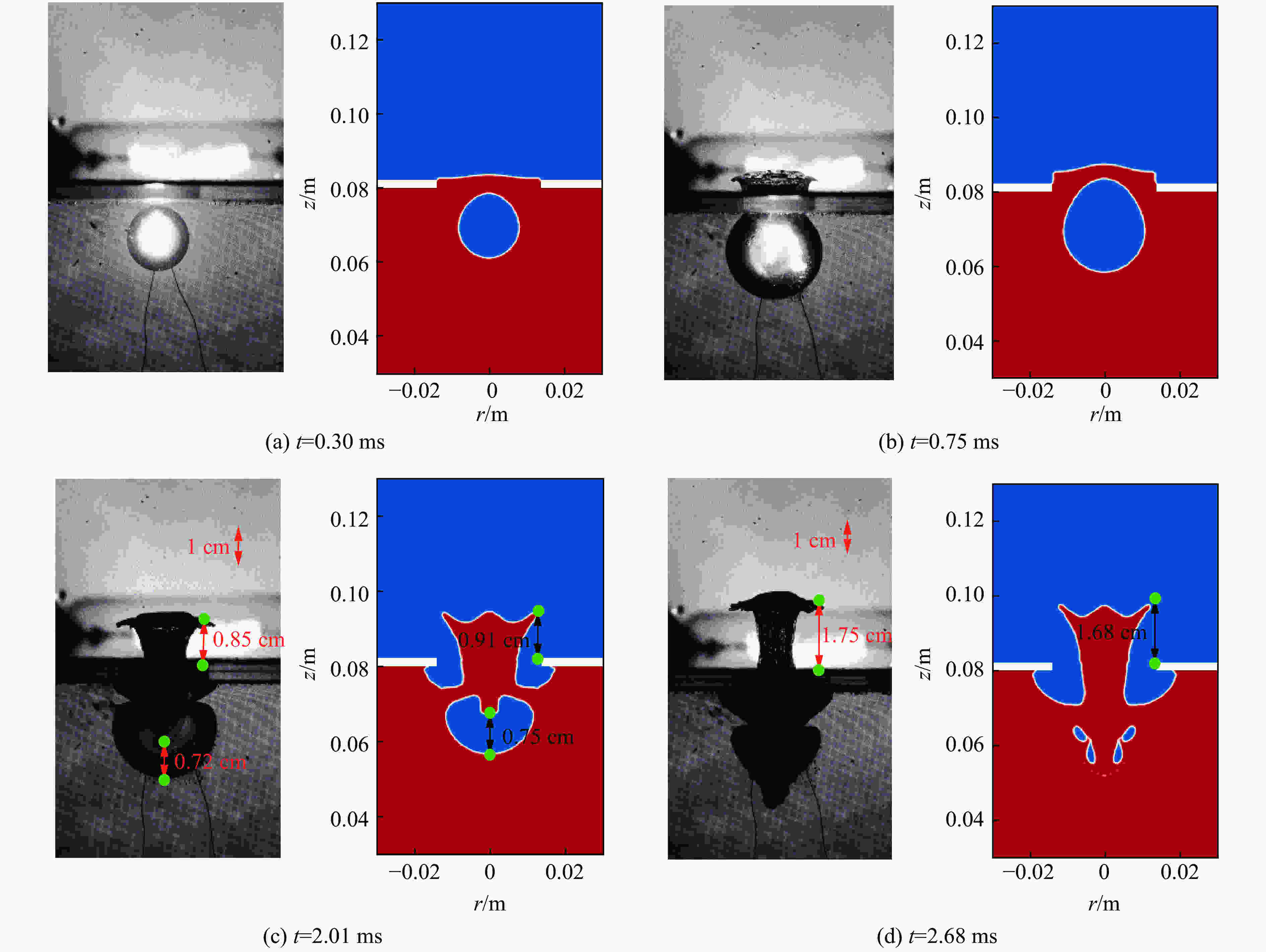
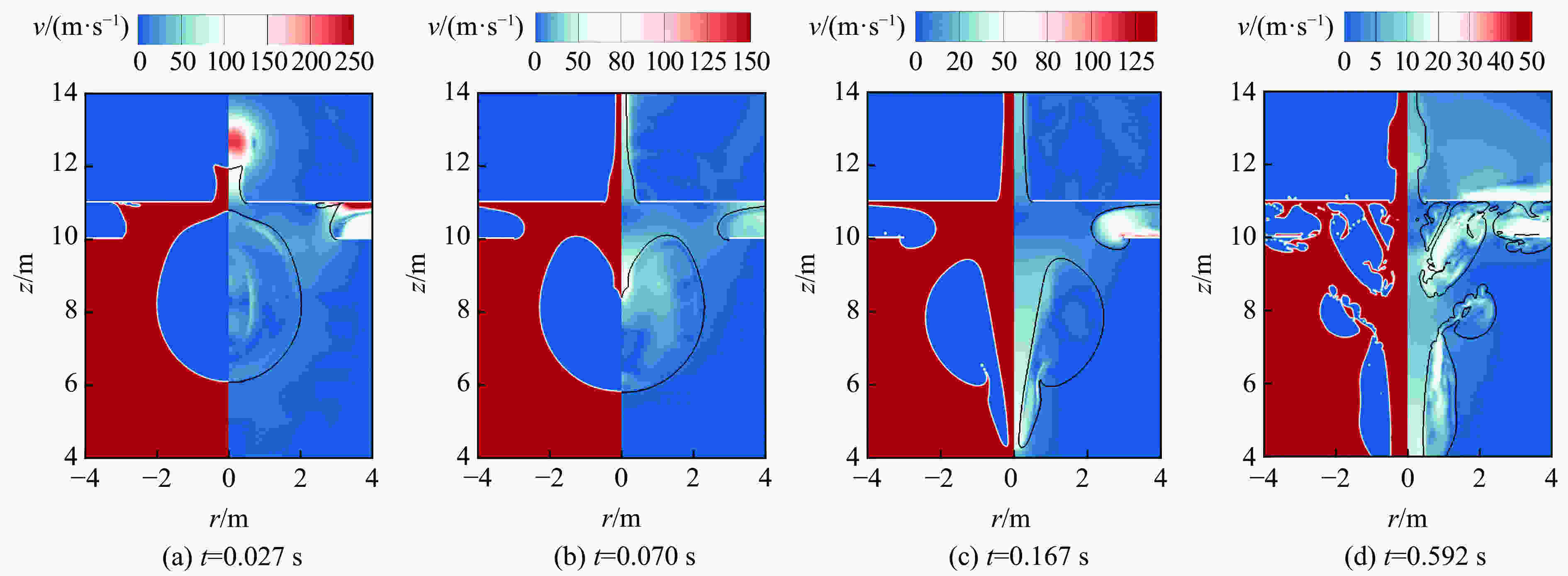
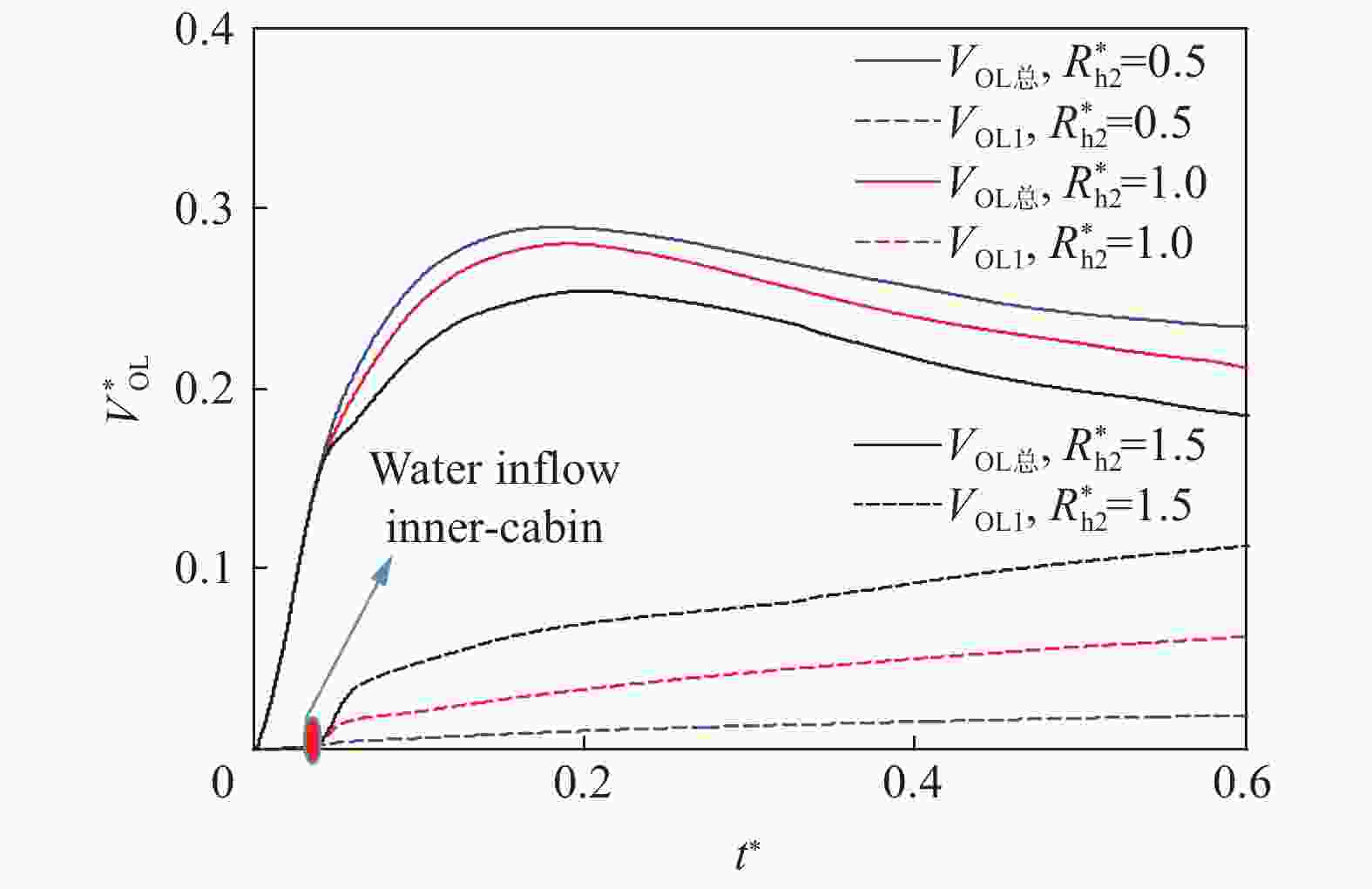
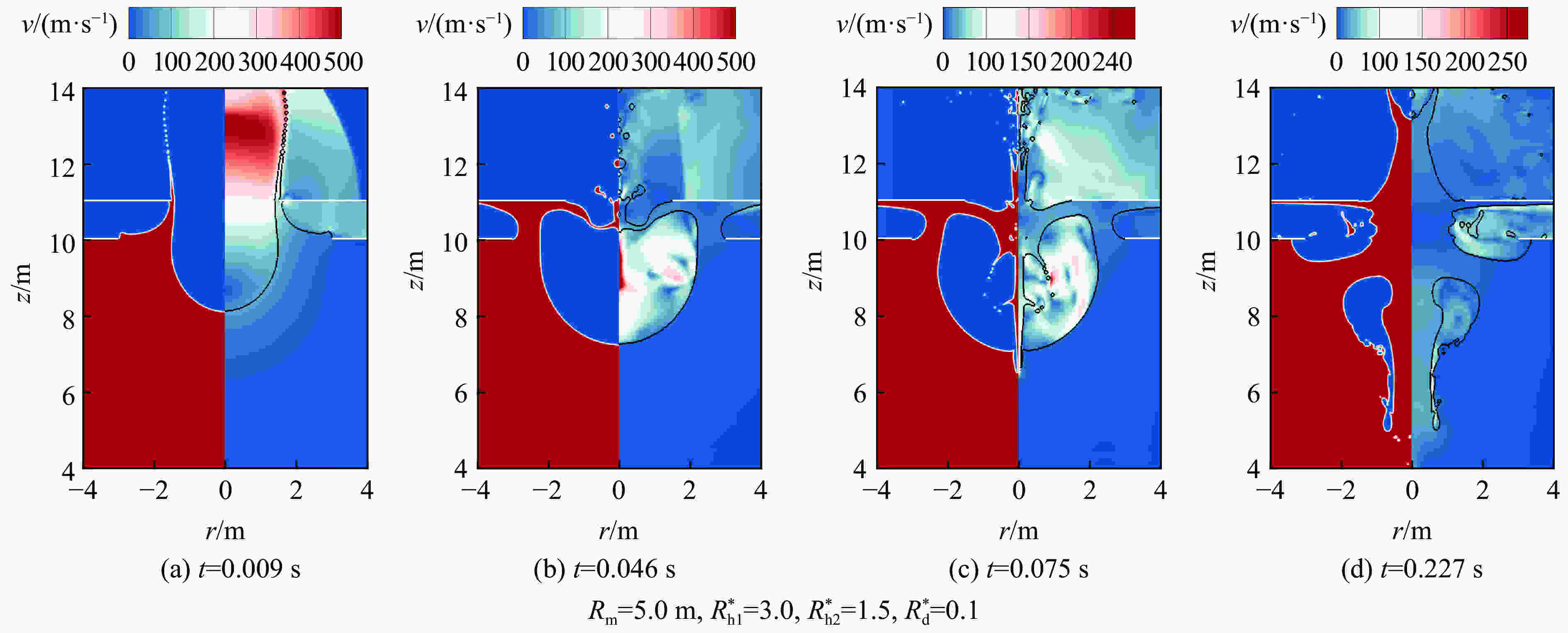
| [1] |
张阿漫, 王诗平, 彭玉祥, 等. 水下爆炸与舰船毁伤研究进展 [J]. 中国舰船研究, 2019, 14(3): 1–13. DOI: 10.19693/j.issn.1673-3185.01608.ZHANG A M, WANG S P, PENG Y X, et al. Research progress in underwater explosion and its damage to ship structures [J]. Chinese Journal of Ship Research, 2019, 14(3): 1–13. DOI: 10.19693/j.issn.1673-3185.01608.
|
| [2] |
金键, 朱锡, 侯海量, 等. 水下爆炸载荷下舰船响应与毁伤研究综述 [J]. 水下无人系统学报, 2017, 25(6): 396–409. DOI: 10.11993/j.issn.2096-3920.2017.05.002.JIN J, ZHU X, HOU H L, et al. Review of dynamic response and damage mechanism of ship structure subjected to underwater explosion load [J]. Journal of Unmanned Undersea Systems, 2017, 25(6): 396–409. DOI: 10.11993/j.issn.2096-3920.2017.05.002.
|
| [3] |
KLASEBOER E, KHOO B C, HUNG K C. Dynamics of an oscillating bubble near a floating structure [J]. Journal of Fluids and Structures, 2005, 21(4): 395–412. DOI: 10.1016/j.jfluidstructs.2005.08.006.
|
| [4] |
WANG S P, ZHANG A M, LIU Y L et al. Bubble dynamics and its applications [J]. Journal of Hydrodynamics, 2018, 30(6): 975–91. DOI: 10.1007/s42241-018-0141-3.
|
| [5] |
张洪, 吴红波, 夏曼曼, 等. 水下爆炸边界效应的研究进展 [J]. 煤矿爆破, 2018(5): 1–5.ZHANG H, WU H B, XIA M M, et al. Research progress of the boundary effect on underwater blasting [J]. Coal Mine Blasting, 2018(5): 1–5.
|
| [6] |
张弩, 宗智. 水下爆炸气泡载荷作用下船体梁的动态水弹性响应 [J]. 船舶力学, 2015, 19(5): 582–591. DOI: 10.3969/j.issn.1007-7294.2015.05.013.ZHANG N, ZONG Z. Dynamic hydro-elastic response of a ship hull girder subjected to underwater explosion bubbles [J]. Journal of Ship Mechanics, 2015, 19(5): 582–591. DOI: 10.3969/j.issn.1007-7294.2015.05.013.
|
| [7] |
GAO J G, CHEN Z H, HUANG Z G et al. Numerical investigations on the oblique water entry of high-speed projectiles [J]. Applied Mathematics and Computation, 2019, 362: 124547. DOI: 10.1016/j.amc.2019.06.061.
|
| [8] |
张振华, 牟金磊, 陈崧, 等. 大型水面舰艇在重型鱼雷水下近距爆炸作用下的毁伤效应 [J]. 海军工程大学学报, 2013, 25(1): 48–53. DOI: 10.7495/j.issn.1009-3486.2013.01.006.ZHANG Z H, MU J L, CHEN S, et al. Anomalous dynamic response of ship beam to near-field underwater explosion of heavy torpedo [J]. Journal of Naval University of Engineering, 2013, 25(1): 48–53. DOI: 10.7495/j.issn.1009-3486.2013.01.006.
|
| [9] |
殷彩玉, 金泽宇, 谌勇, 等. 多孔覆盖层水下爆炸流固耦合分析 [J]. 振动与冲击, 2017, 36(12): 7–11; 49. DOI: 10.13465/j.cnki.jvs.2017.12.002.YIN C Y, JIN Z Y, CHEN Y, et al. Fluid-structure interaction effects of cellular claddings to underwater explosion [J]. Journal of Vibration and Shock, 2017, 36(12): 7–11; 49. DOI: 10.13465/j.cnki.jvs.2017.12.002.
|
| [10] |
张伦平, 潘建强, 刘建湖, 等. 多层结构水下爆炸破坏效应研究 [C] // 第十届全国冲击动力学讨论会论文集. 太原: 中国力学学会, 2011: 1−13.
|
| [11] |
ZHANG A M, CUI P, CUI J, et al. Experimental study on bubble dynamics subject to buoyancy [J]. Journal of Fluid Mechanics, 2015, 776: 137–60. DOI: 10.1017/jfm.2015.323.
|
| [12] |
LIU Y L, WANG S P, ZHANG A M. Interaction between bubble and air-backed plate with circular hole [J]. Physics of Fluids, 2016, 28(6): 062105. DOI: 10.1063/1.4953010.
|
| [13] |
LIU N N, WU W B, ZhANG A M et al. Experimental and numerical investigation on bubble dynamics near a free surface and a circular opening of plate [J]. Physics of Fluids, 2017, 29(10): 107102. DOI: 10.1063/1.4999406.
|
| [14] |
刘润泉, 白雪飞, 朱锡. 舰船单元结构模型水下接触爆炸破口试验研究 [J]. 海军工程大学学报, 2001, 13(5): 41–46. DOI: 10.3969/j.issn.1009-3486.2001.05.011.LIU R Q, BAI X F, ZHU X, et al. Breach experiment research of vessel element structure models subjected to underwater contact explosion [J]. Journal of Naval University of Engineering, 2001, 13(5): 41–46. DOI: 10.3969/j.issn.1009-3486.2001.05.011.
|
| [15] |
李金河, 汪斌, 王彦平, 等. 不同装药形状TNT水中爆炸近场冲击波传播的实验研究 [J]. 火炸药学报, 2018, 41(5): 461–464; 500. DOI: 10.14077/j.issn.1007-7812.2018.05.007.LI J H, WANG B, WANG Y P, et al. Experimental study on near-field shock wave propagation of underwater explosion of TNT with different charge shapes [J]. Chinese Journal of Explosives & Propellants, 2018, 41(5): 461–464; 500. DOI: 10.14077/j.issn.1007-7812.2018.05.007.
|
| [16] |
杨棣, 姚熊亮, 王军, 等. 接触爆炸载荷作用下船体板架破口大小的预测 [J]. 中国造船, 2014, 55(2): 77–84. DOI: 10.3969/j.issn.1000-4882.2014.02.009.YANG D, YAO X L, WANG J, et al. Forecast of crevasse size of hull grillage in contact explosion [J]. Shipbuilding of China, 2014, 55(2): 77–84. DOI: 10.3969/j.issn.1000-4882.2014.02.009.
|
| [17] |
LI S, Li Y B, ZHANG A M. Numerical analysis of the bubble jet impact on a rigid wall [J]. Applied Ocean Research, 2015, 50: 227–236. DOI: 10.1016/j.apor.2015.02.003.
|
| [18] |
汪浩, 程远胜, 刘均, 等. 新型矩形蜂窝夹芯夹层加筋圆柱壳抗水下爆炸冲击载荷分析 [J]. 振动与冲击, 2011, 30(1): 162–166; 226. DOI: 10.3969/j.issn.1000-3835.2011.01.036.WANG H, CHENG Y S, LIU J, et al. Anti-shock analysis for new type rectangular honeycomb sandwich stiffened cylindrical shells subjected to underwater explosion shock load [J]. Journal of Vibration and Shock, 2011, 30(1): 162–166; 226. DOI: 10.3969/j.issn.1000-3835.2011.01.036.
|
| [19] |
ZHANG A M, LIU Y L. Improved three-dimensional bubble dynamics model based on boundary element method [J]. Journal of Computational Physics, 2015, 294: 208–223. DOI: 10.1016/j.jcp.2015.03.049.
|
| [20] |
LI T, WANG S P, LI S, et al. Numerical investigation of an underwater explosion bubble based on FVM and VOF [J]. Applied Ocean Research, 2018, 74: 49–58. DOI: 10.1016/j.apor.2018.02.024.
|
| [21] |
王志凯, 周鹏, 孙波, 等. 气泡及其破碎兴波对浮动冲击平台影响探究 [J]. 爆炸与冲击, 2019, 39(9): 093201. DOI: 10.11883/bzycj-2018-0212.WANG Z K, ZHOU P, SUN B, et al. Influence of bubbles and breaking waves on floating shock platform [J]. Explosion and Shock Waves, 2019, 39(9): 093201. DOI: 10.11883/bzycj-2018-0212.
|
| [22] |
BENSON D J. Computational methods in lagrangian and eulerian hydrocodes [J]. Computer Methods in Applied Mechanics and Engineering, 1992, 99(2−3): 235–394. DOI: 10.1016/0045-7825(92)90042-I.
|
| [23] |
LIU Y L, ZHANG A M, TIAN Z L, et al. Investigation of free-field underwater explosion with Eulerian finite element method [J]. Ocean Engineering, 2018, 166: 182–190. DOI: 10.1016/j.oceaneng.2018.08.001.
|
| [24] |
HE M, ZHANG A M, LIU Y L. Prolonged simulation of near-free surface underwater explosion based on Eulerian finite element method [J]. Theoretical and Applied Mechanics Letters, 2020, 10(1): 16–22. DOI: 10.1016/j.taml.2020.01.003.
|
| [25] |
TIAN Z L, LIU Y L, ZHANG A M, et al. Energy dissipation of pulsating bubbles in compressible fluids using the Eulerian finite-element method [J]. Ocean Engineering, 2020, 196: 106714. DOI: 10.1016/j.oceaneng.2019.106714.
|
| [26] |
QIU J X, LIU T G, KHOO B C. Simulations of compressible two-medium flow by Runge-Kutta discontinuous Galerkin methods with ghost fluid method [J]. Communications in Computational Physics, 2008, 3(2): 479–504.
|
| [27] |
FELIPPA C A. A family of early-time approximations for fluid-structure interaction [J]. Journal of Applied Mechanics, 1980, 47(4): 703–708. DOI: 10.1115/1.3153777.
|






 下载:
下载: