Thermal relaxation responses of graded materials satisfing power law
-
摘要: 梯度材料热弛豫响应行为的理论研究对于热分析具有重要意义。结合Cattaneo-Vernotte线性双曲型热传导方程,推导得到幂律梯度材料的一维双曲型非傅里叶热传导方程。通过积分变换法,解得频域内温度场的贝塞尔级数形式解,随后利用极点留数法,得到时间域内温度场的第一类解析解。在第一类解析解的基础上,由简化欧拉方程解得第二类解析解。结合拉普拉斯数值逆变换方法,验证了解析解的准确性。以高温阻热梯度材料Mo-ZrC的应用为例,讨论了一般温度边界条件以及温度脉冲载荷作用下幂律梯度材料的热弛豫响应行为。分析发现,在所研究范围内温度场具备波动和传导衰减的双重特性。响应时间和温度幅值随着热弛豫时间系数的增大而增大,温度场分布和单元波形与梯度结构相关。
-
关键词:
- 热弛豫响应 /
- Mo-ZrC梯度材料 /
- 贝塞尔级数 /
- 拉普拉斯变换
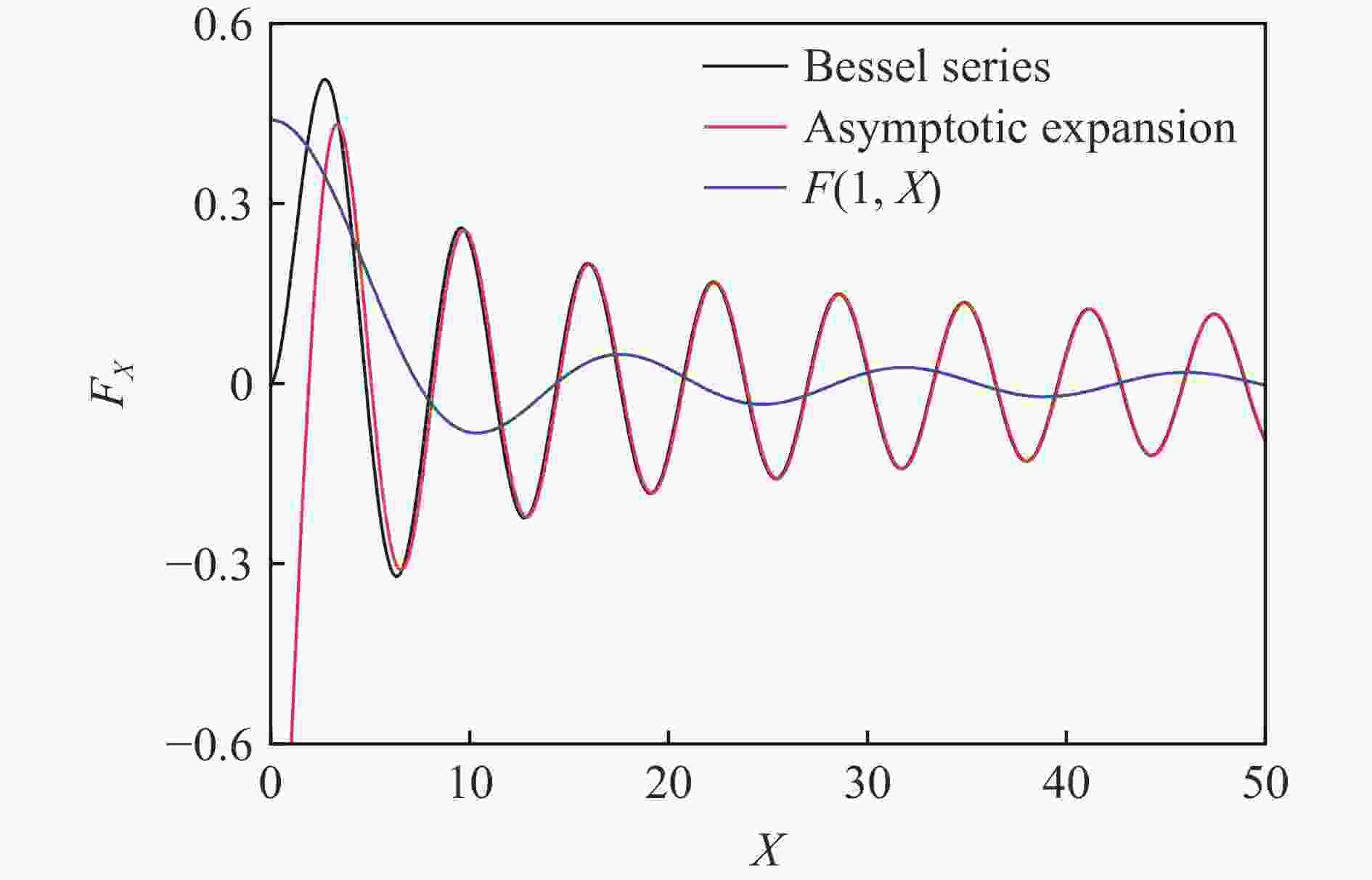
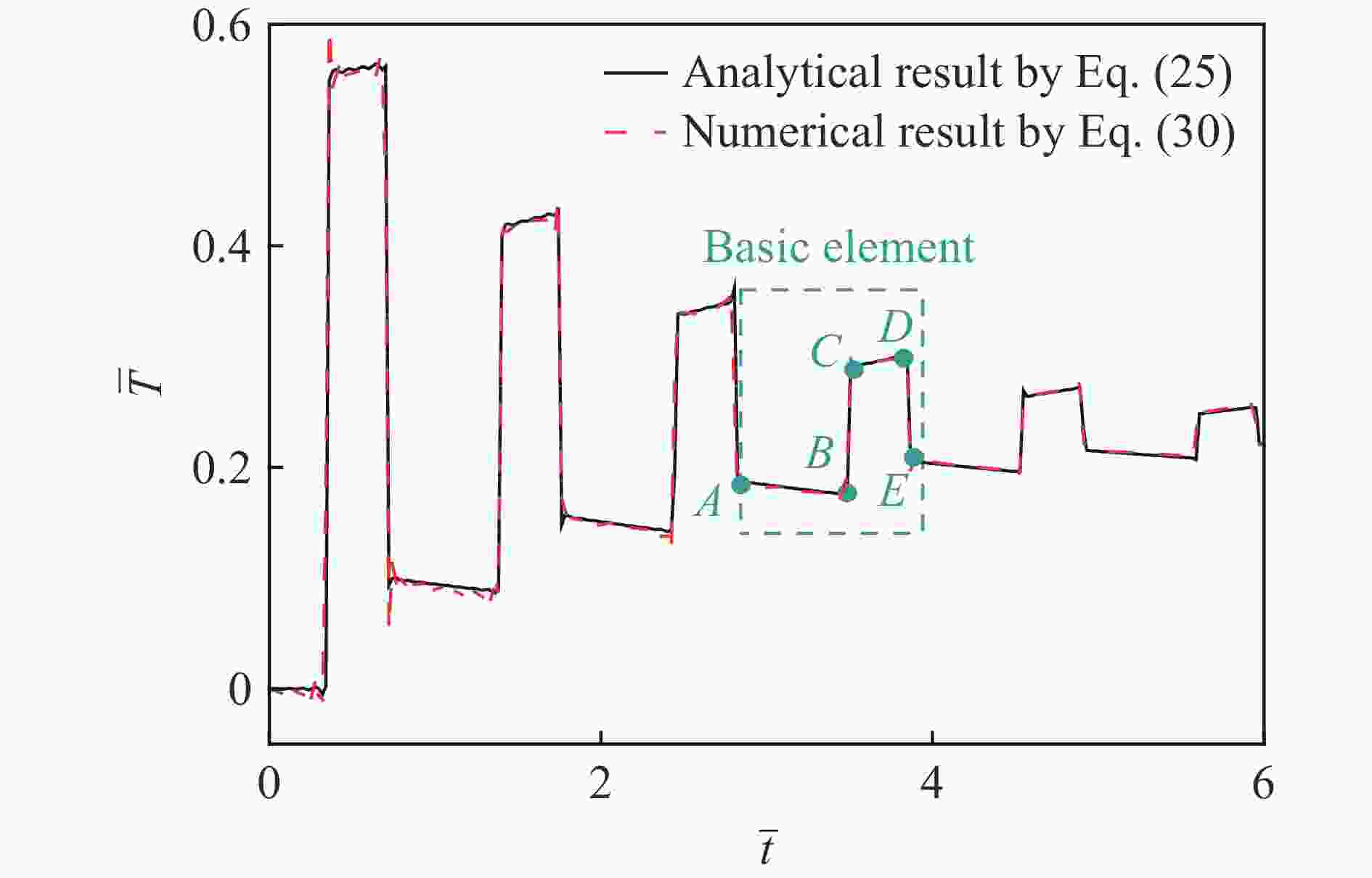
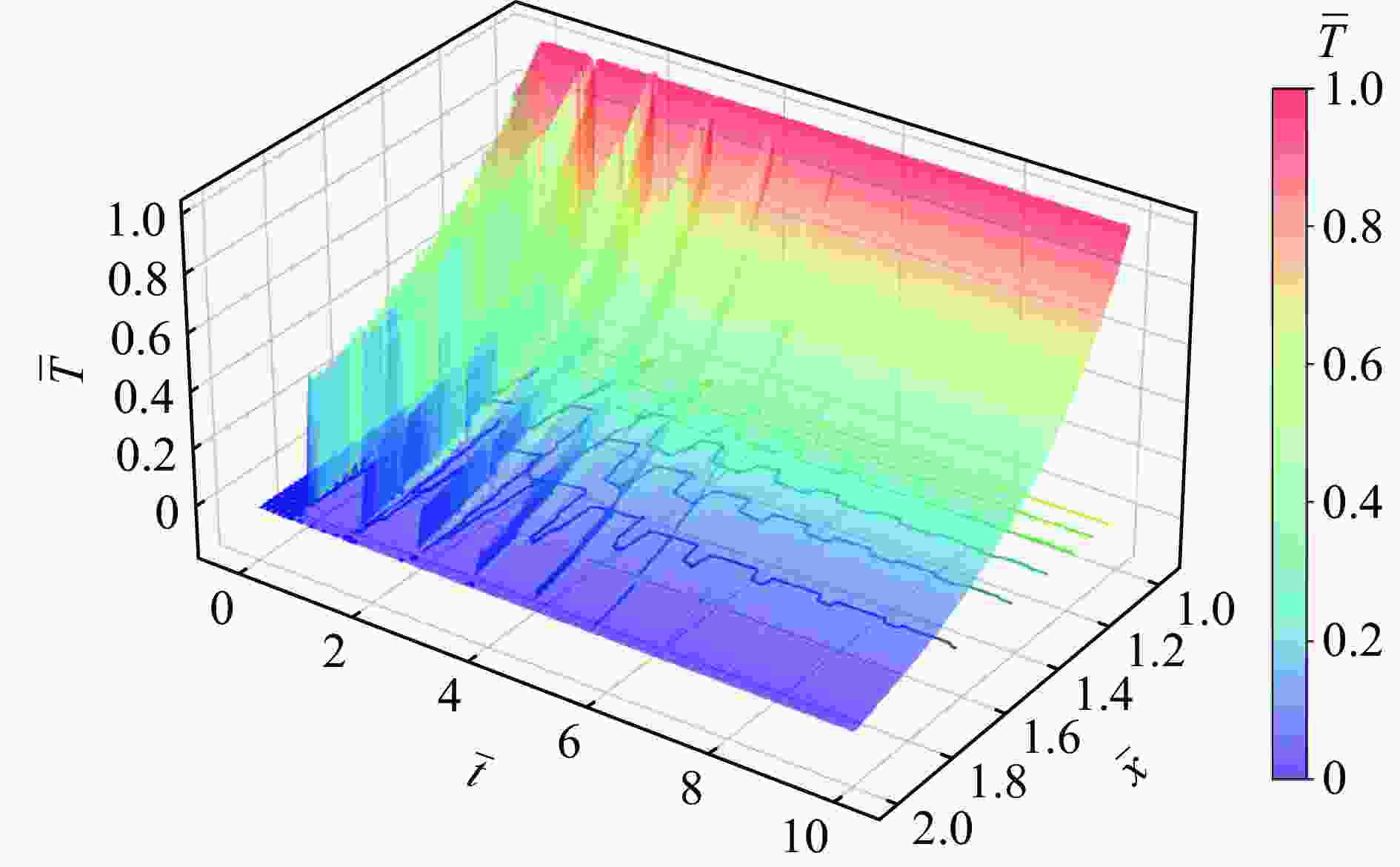
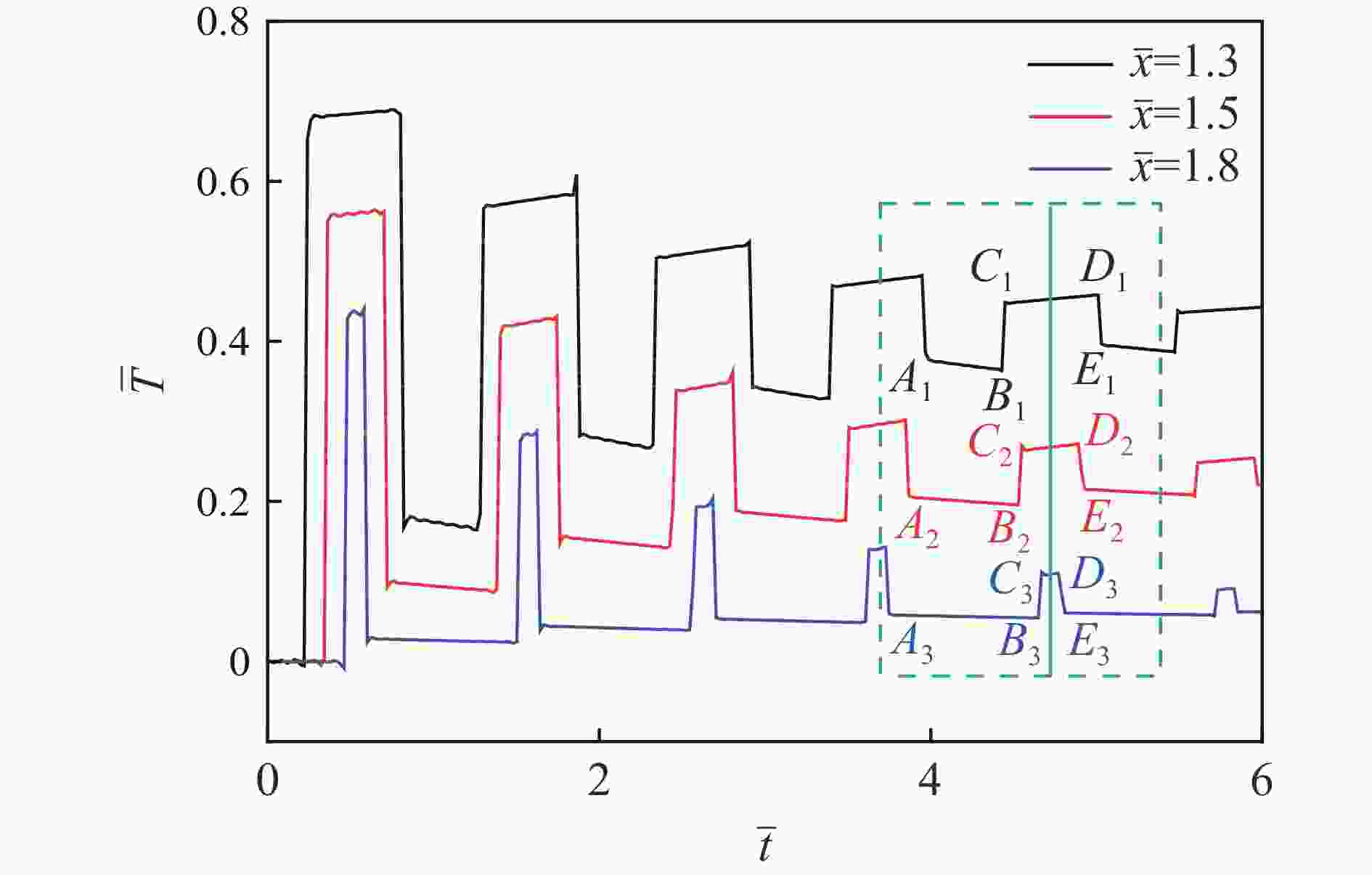
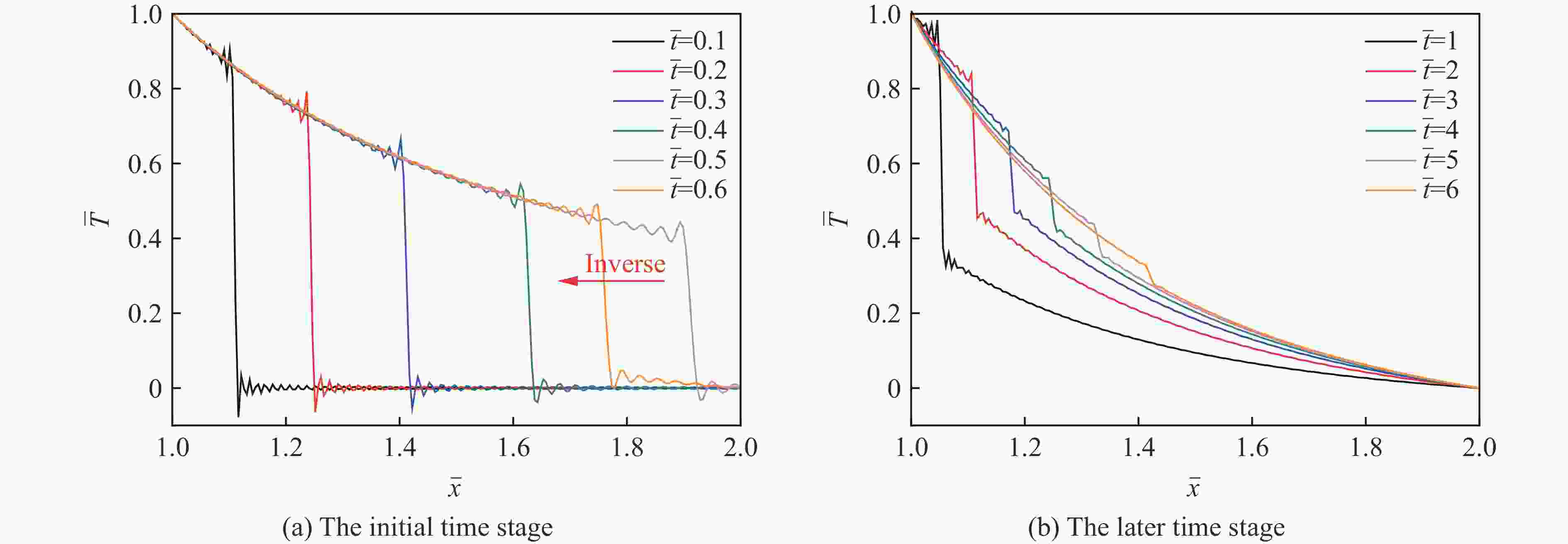
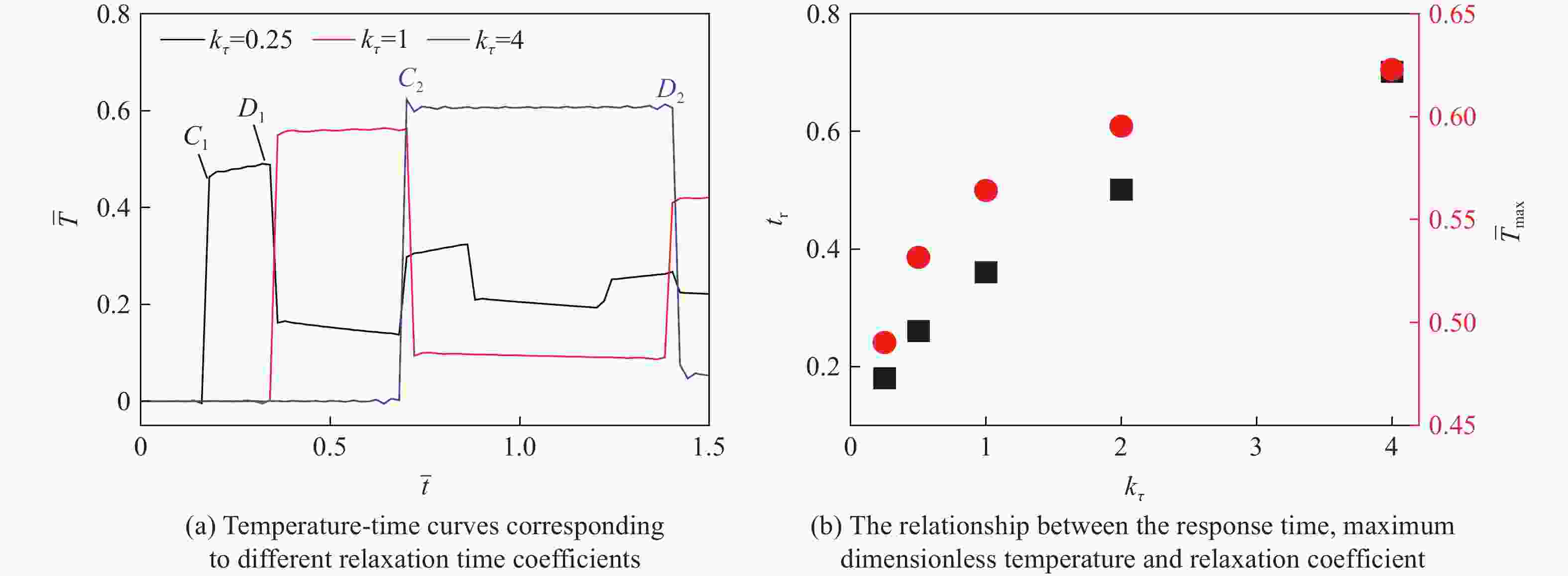
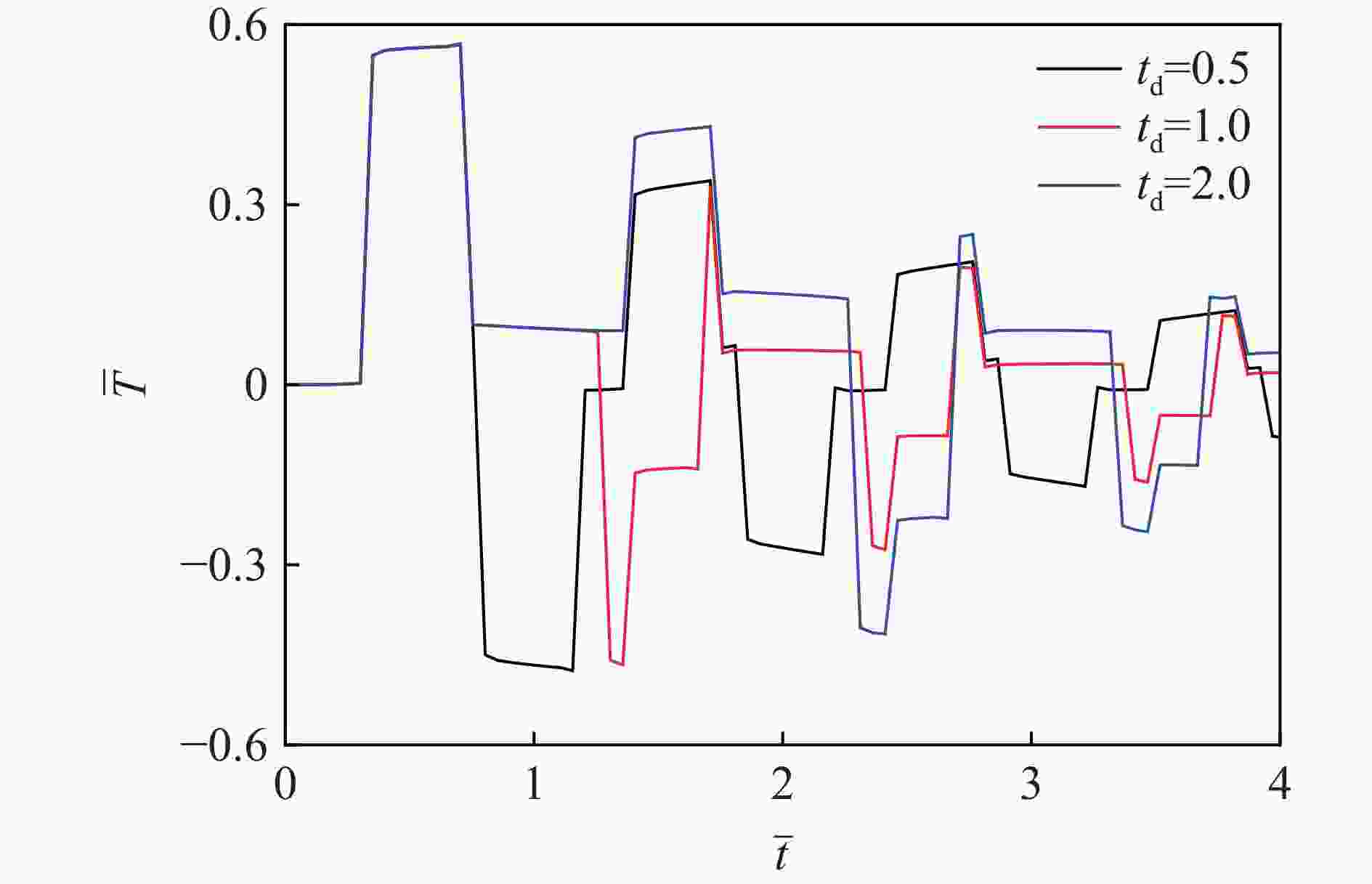
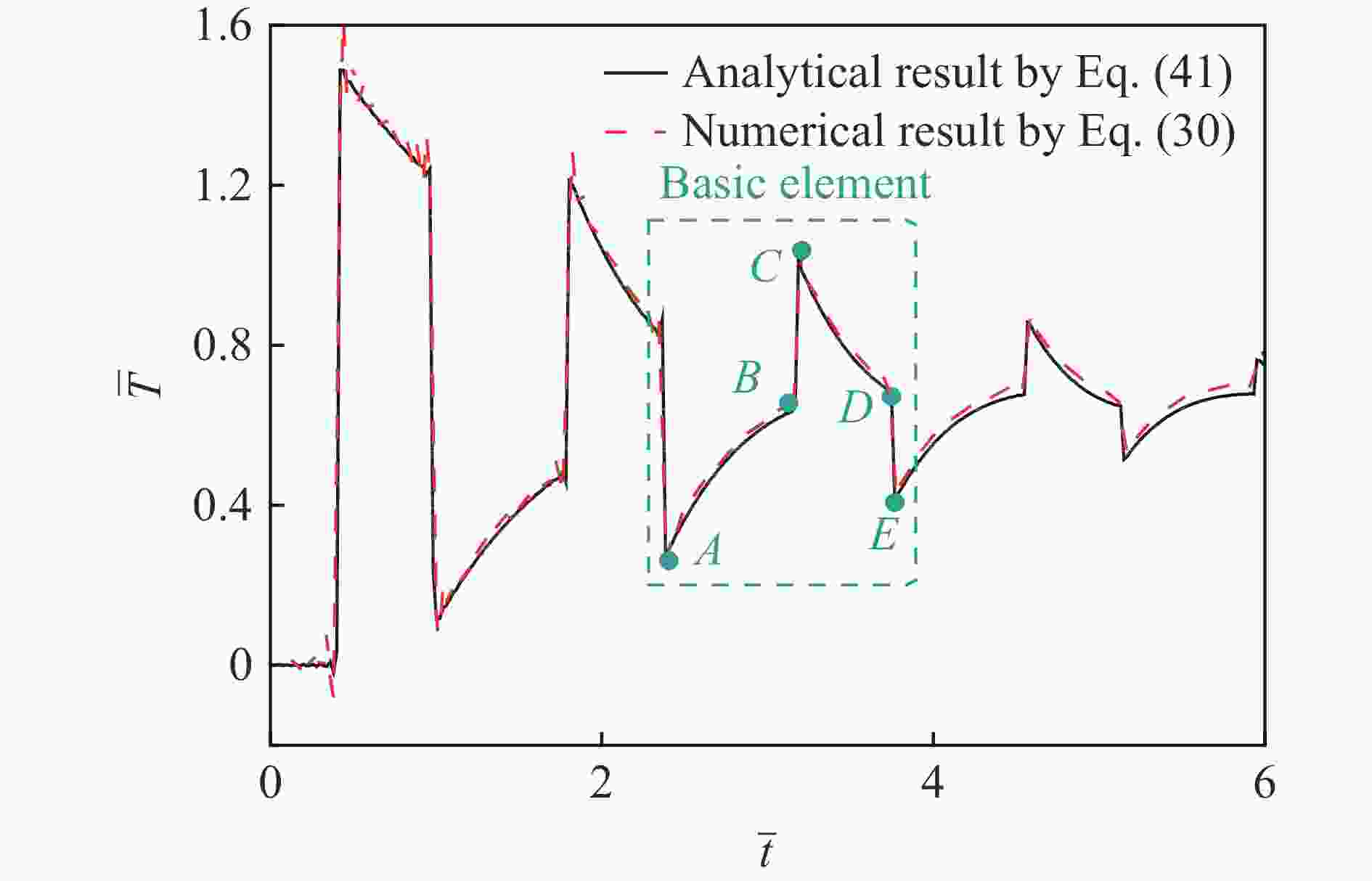
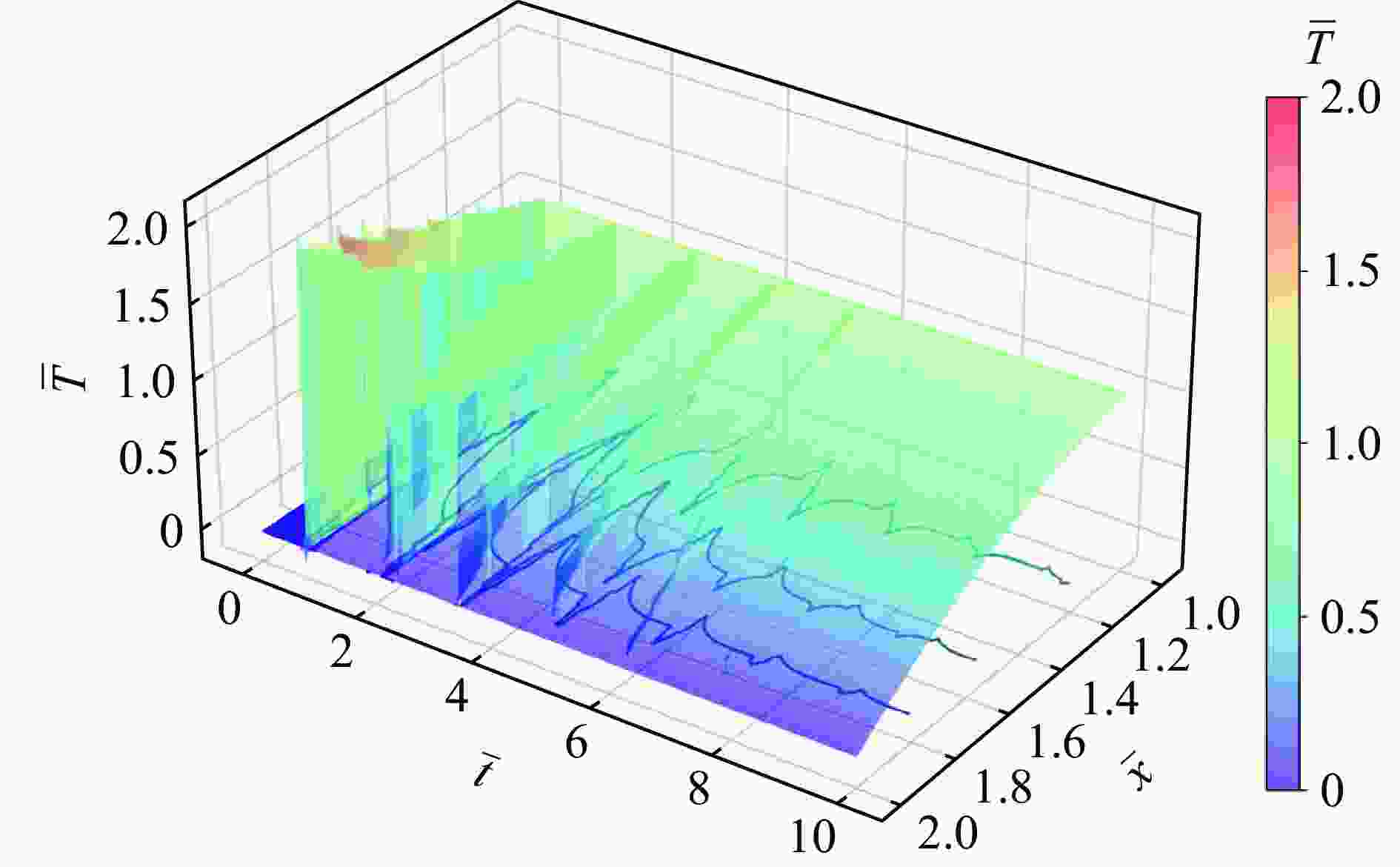
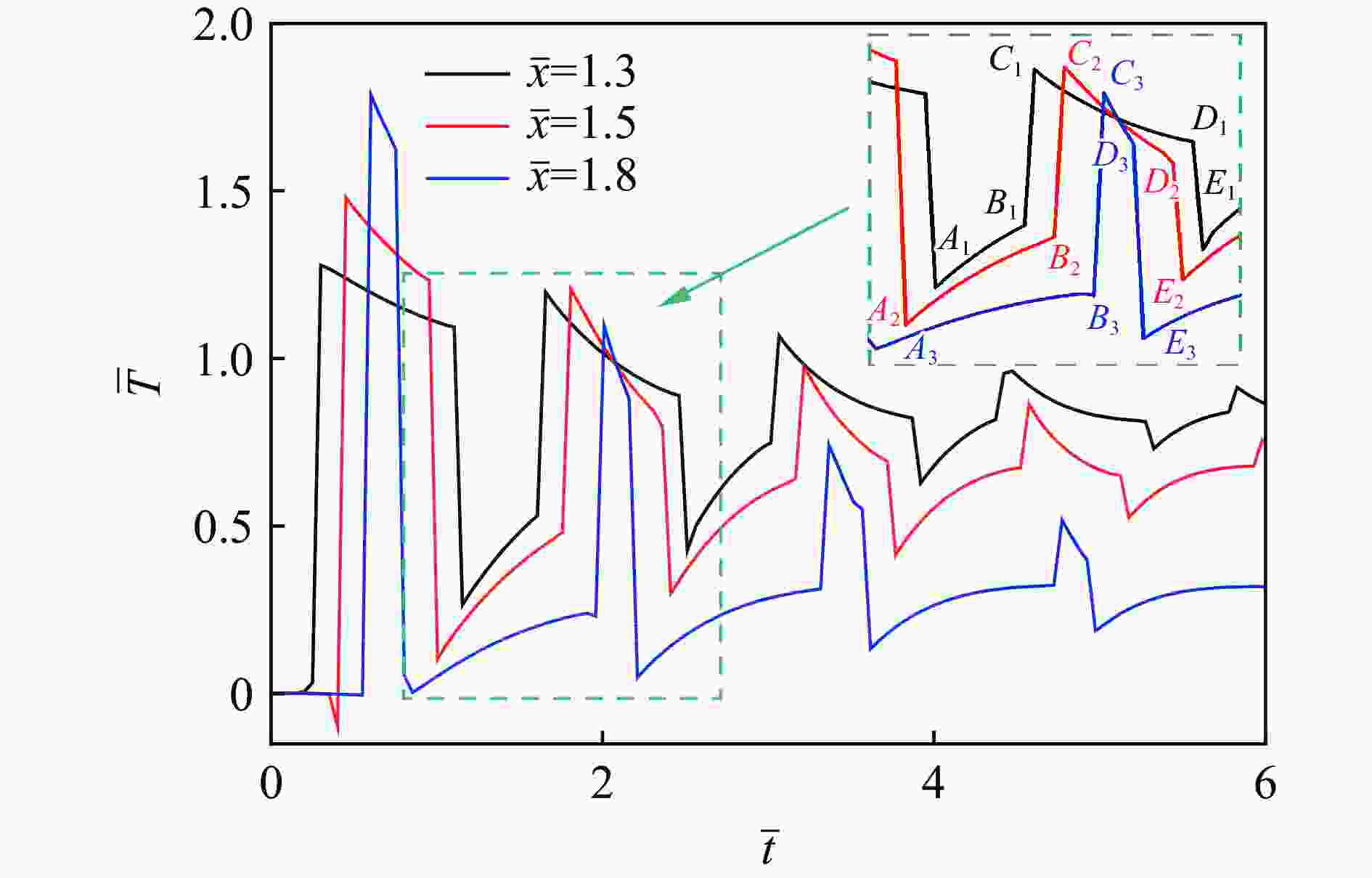
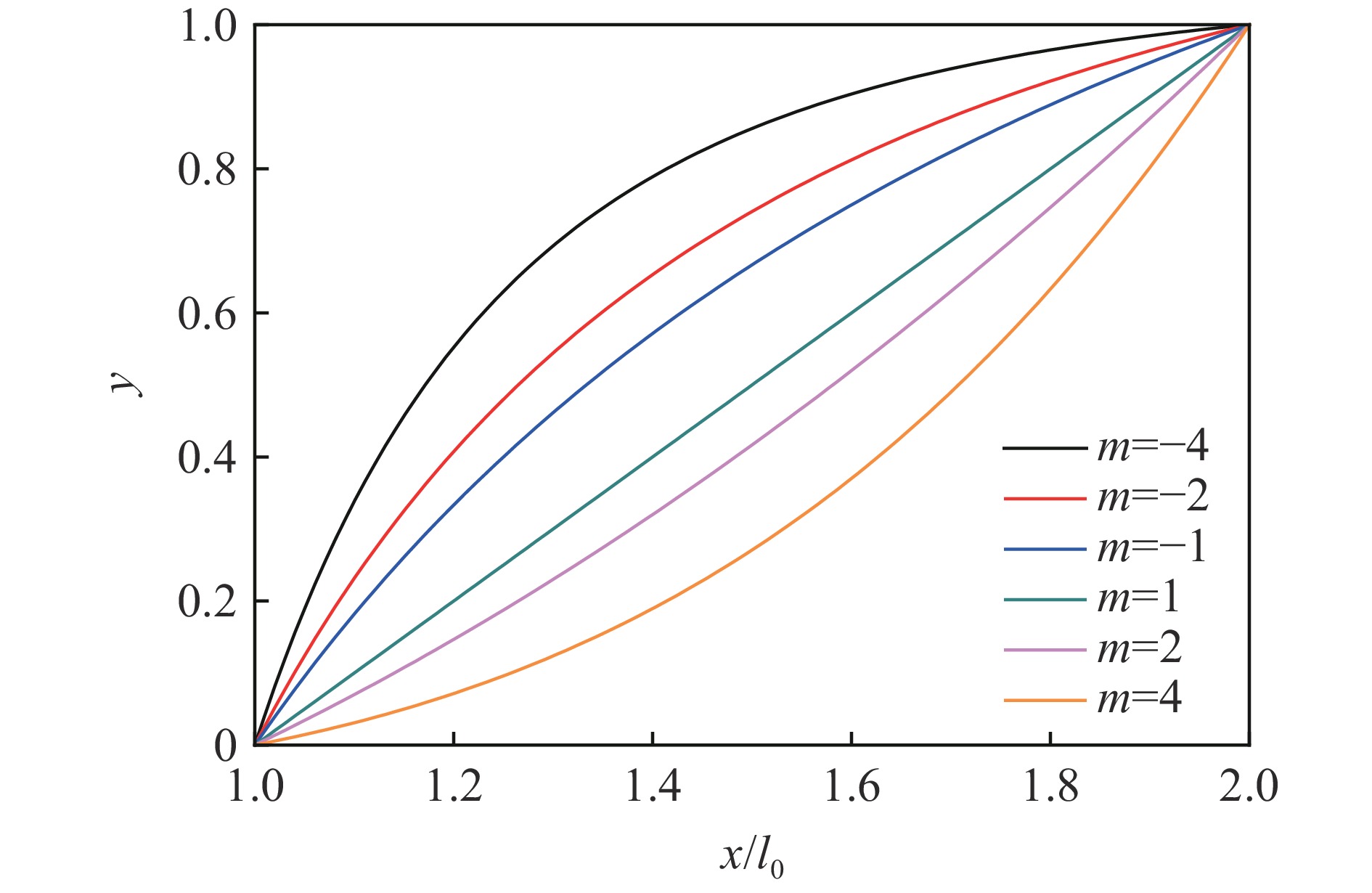
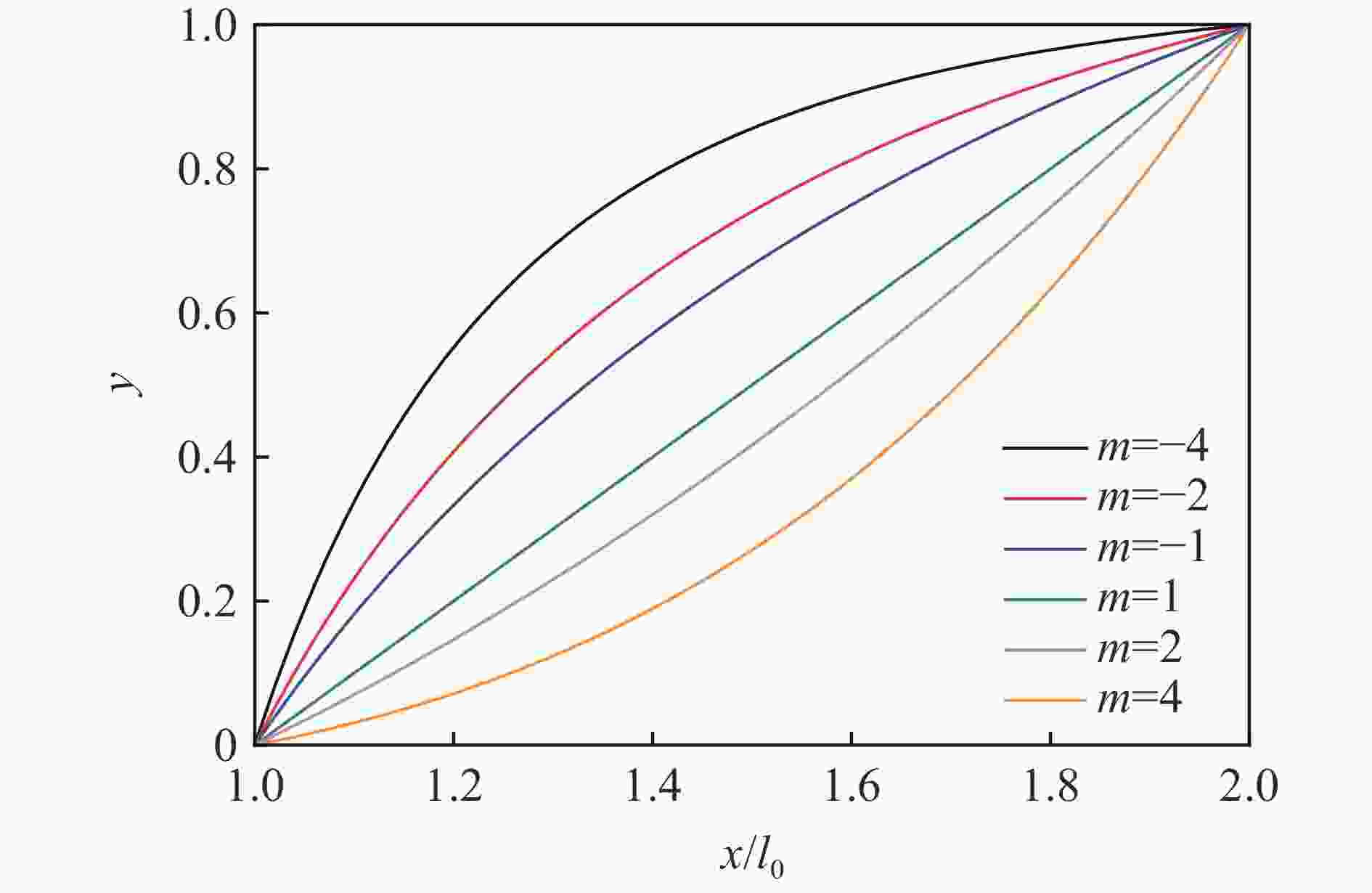
Abstract: To study the thermal relaxation behavior of graded media that satisfies the power law, a one-dimensional hyperbolic non-Fourier heat conduction equation of the graded material which satisfies the power law was derived from the Cattaneo-Vernotte linear hyperbolic heat transfer equation with the thermal relaxation coefficient and graded exponent induced. The equation was first treated dimensionless. Based on the Laplace transformation, the new heat conduction equation was found to conform to the general form of the Bessel equation called the Lommel equation in the frequency domain, and the Bessel series solution of the temperature field in the frequency domain was obtained. With the asymptotic expansion of the Bessel series, a simplified expression of the temperature field in the frequency domain containing trigonometric function was obtained. The inverse Laplace transformation of the temperature field in the frequency domain was employed to get the first analytical solution of the temperature field in the time domain. Besides the first analytical solution, the new heat conduction equation in the frequency domain was simplified to the Euler equation, and the second kind of analytical solution was obtained by the pole residue method. The second analytical solution exhibits similar fluctuation attenuation and diffusion features, and both the waveform and response time are sensitive to the relaxation time coefficient. However, the second kind of analytical solution differs from the first kind of solution in terms of waveform elements which are highly related to the graded structure. The accuracy of the analytical result is verified by numerical calculation. Taking Mo-ZrC graded composite as an example, the thermal relaxation behavior of graded material that satisfies power law under the first kind of temperature boundary and temperature pulse loading are discussed in detail. The temperature field shows both fluctuation attenuation and conduction characteristics. With the increase of the thermal relaxation coefficient, the response time and temperature wave amplitude increase, the unit waveform develops from a trapezoidal wave to a rectangular wave, and the oscillation approaching the boundary shows an obvious bias. -
表 1 Mo和ZrC的热力学参数
Table 1. Thermomechanical properties of Mo and ZrC
材料 密度/(kg·m−3) 比热容/(J·kg−1·K−1) 导热系数/(W·m−1·K−1) 熔点/℃ 杨氏模量/GPa 泊松比 Mo 10200 230 150 3400 279 0.32 ZrC 6510 310 10 2620 390 0.191 -
[1] SALEH B, JIANG J H, FATHI R, et al. 30 years of functionally graded materials: an overview of manufacturing methods, applications and future challenges [J]. Composites Part B: Engineering, 2020, 201: 108376. DOI: 10.1016/j.compositesb.2020.108376. [2] GHASEMI M H, HOSEINZADEH S, MEMON S. A dual-phase-lag (DPL) transient non-Fourier heat transfer analysis of functional graded cylindrical material under axial heat flux [J]. International Communications in Heat and Mass Transfer, 2022, 131: 105858. DOI: 10.1016/j.icheatmasstransfer.2021.105858. [3] DAI H L, RAO Y N, DAI T. A review of recent researches on FGM cylindrical structures under coupled physical interactions, 2000–2015 [J]. Composite Structures, 2016, 152: 199–225. DOI: 10.1016/j.compstruct.2016.05.042. [4] PARIHAR R S, SETTI S G, SAHU R K. Recent advances in the manufacturing processes of functionally graded materials: a review [J]. Science and Engineering of Composite Materials, 2018, 25(2): 309–336. DOI: 10.1515/secm-2015-0395. [5] 谢雨珊, 陆建华, 徐松林, 等. Mo-ZrC梯度金属陶瓷的冲击响应行为 [J]. 爆炸与冲击, 2023, 43(3): 033101. DOI: 10.11883/bzycj-2022-0374.XIE Y S, LU J H, XU S L, et al. On impact properties of Mo-ZrC gradient metal ceramics [J]. Explosion and Shock Waves, 2023, 43(3): 033101. DOI: 10.11883/bzycj-2022-0374. [6] SALEH B, JIANG J H, FATHI R, et al. Study of the microstructure and mechanical characteristics of AZ91-SiCP composites fabricated by stir casting [J]. Archives of Civil and Mechanical Engineering, 2020, 20(3): 71. DOI: 10.1007/s43452-020-00071-9. [7] CHI S H, CHUNG Y L. Mechanical behavior of functionally graded material plates under transverse load. part I: analysis [J]. International Journal of Solids and Structures, 2006, 43(13): 3657–3674. DOI: 10.1016/j.ijsolstr.2005.04.011. [8] CHANDRASEKHARAIAH D S. Thermoelasticity with second sound: a review [J]. Applied Mechanics Reviews, 1986, 39(3): 355–376. DOI: 10.1115/1.3143705. [9] BABAEI M H, CHEN Z T. Hyperbolic heat conduction in a functionally graded hollow sphere [J]. International Journal of Thermophysics, 2008, 29(4): 1457–1469. DOI: 10.1007/s10765-008-0502-1. [10] JIANG F M. Non-Fourier heat conduction phenomena in porous material heated by microsecond laser pulse [J]. Microscale Thermophysical Engineering, 2003, 6(4): 331–346. DOI: 10.1080/10893950290098386. [11] CHANDRASEKHARAIAH D S. Hyperbolic thermoelasticity: a review of recent literature [J]. Applied Mechanics Reviews, 1998, 51(12): 705–729. DOI: 10.1115/1.3098984. [12] BUCĂ A M, OANE M, MAHMOOD M A, et al. Non-Fourier estimate of electron temperature in case of femtosecond laser pulses interaction with metals [J]. Metals, 2020, 10(5): 606. DOI: 10.3390/met10050606. [13] CHEN G. Non-Fourier phonon heat conduction at the microscale and nanoscale [J]. Nature Reviews Physics, 2021, 3(8): 555–569. DOI: 10.1038/s42254-021-00334-1. [14] SELLITTO A, CARLOMAGNO I, DI DOMENICO M. Nonlocal and nonlinear effects in hyperbolic heat transfer in a two-temperature model [J]. Zeitschrift für Angewandte Mathematik und Physik, 2021, 72(1): 7. DOI: 10.1007/s00033-020-01435-0. [15] POURASGHAR A, CHEN Z. Heat waves interference regarding dual-phase-lag, hyperbolic and Fourier heat conduction in CNT reinforced composites under a thermal shock [J]. Waves in Random and Complex Media, 2022, 32(3): 1198–1214. DOI: 10.1080/17455030.2020.1813351. [16] XU B B, GAO X W, CUI M. High precision simulation and analysis of non-Fourier heat transfer during laser processing [J]. International Journal of Heat and Mass Transfer, 2021, 178: 121574. DOI: 10.1016/j.ijheatmasstransfer.2021.121574. [17] PENG Y, ZHANG X Y, XIE Y J, et al. Transient hygrothermoelastic response in a cylinder considering non-Fourier hyperbolic heat-moisture coupling [J]. International Journal of Heat and Mass Transfer, 2018, 126: 1094–1103. DOI: 10.1016/j.ijheatmasstransfer.2018.05.084. [18] JIANG F M. Solution and analysis of hyperbolic heat propagation in hollow spherical objects [J]. Heat and Mass Transfer, 2006, 42(12): 1083–1091. DOI: 10.1007/s00231-005-0066-6. [19] KELES I, CONKER C. Transient hyperbolic heat conduction in thick-walled FGM cylinders and spheres with exponentially-varying properties [J]. European Journal of Mechanics A/Solids, 2011, 30(3): 449–455. DOI: 10.1016/j.euromechsol.2010.12.018. [20] KATOH Y, VASUDEVAMURTHY G, NOZAWA T, et al. Properties of zirconium carbide for nuclear fuel applications [J]. Journal of Nuclear Materials, 2013, 441(1/2/3): 718–742. DOI: 10.1016/j.jnucmat.2013.05.037. [21] CHENG J Y, NEMAT-NASSER S, GUO W G. A unified constitutive model for strain-rate and temperature dependent behavior of molybdenum [J]. Mechanics of Materials, 2001, 33(11): 603–616. DOI: 10.1016/S0167-6636(01)00076-X. [22] ELISHAKOFF I, PELLEGRINI F. Exact solutions for buckling of some divergence-type nonconservative systems in terms of Bessel and lommel functions [J]. Computer Methods in Applied Mechanics and Engineering, 1988, 66(1): 107–119. DOI: 10.1016/0045-7825(88)90062-X. [23] URBANOWICZ K, BERGANT A, GRZEJDA R, et al. About inverse Laplace transform of a dynamic viscosity function [J]. Materials, 2022, 15(12): 4364. DOI: 10.3390/ma15124364. -






 下载:
下载: