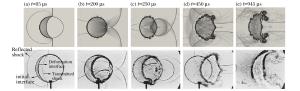
Influence of magnetic field on interaction of shock wave with R22 heavy gas column
-
摘要: 为研究平面入射激波与磁化R22重质圆形气柱的作用过程，首先通过数值方法得到了不同初始条件下激波诱导R22气柱的Kelvin-Helmholtz (KH)及Richtmyer-Meshkov (RM)不稳定性导致的重气柱变形过程，并详细讨论了不同情况下透射激波在气柱内聚焦诱导射流的过程；然后在加入磁场的情况下，采用CTU+CT算法进行数值模拟，以保证数值结果满足任意时刻磁场的散度为零。计算结果表明：磁场对激波诱导R22气柱不稳定性具有抑制作用；法向磁场和流向磁场都可以很好地抑制RM不稳定性；对于KH不稳定性，法向磁场的控制效果更好，不仅可以抑制界面上涡串的卷起，还可以阻止主涡的发展，而流向磁场做不到后者；磁场对射流影响不大，射流处的磁能量可以一定程度上抑制射流的衰减，同时法向磁场可以减小聚焦时压力及速度峰值。Abstract: To study the interaction process of the plane incident shock wave with the magnetized R22 heavy gas column, we numerically simulated the deformation process of the shock-wave-induced R22 heavy gas column resulting from Kelvin-Helmholtz (KH) and Richtmyer-Meshkov (RM) instabilities under different initial conditions, and analyzed the jet focusing and inducing process by the transmitted shock wave. When the magnetic field was taken into consideration, the CTU + CT algorithm satisfying the divergence equation of the magnetic field at any time was adopted in the numerical simulation. The results show that the magnetic field is capable of restraining the instability of the shock-wave-induced R22 gas column. Both the normal magnetic field (vertical to the flow direction) and the tangential magnetic field (parallel to the flow direction) can inhibit the RM instability. However, the restraining of the normal magnetic field is more effective than that of the tangential one with regard to the KH instability, as it can not only inhibit the vortex train rolling up on the interface but also prevent the bound vortex from developing. Besides, it is found that the magnetic field has little influence on the jet, and the magnetic energy at the jet point can suppress the jet attenuation to some extent while the normal magnetic field can reduce the peak pressure and velocity when the transmitted shock wave is focused.
-
Key words:
- magnetization gas /
- magneto-hydro-dynamics /
- magnetic field /
- instability /
- shock wave
-
图 3 后期激波与R22气柱作用过程计算纹影
Figure 3. Numerical results of the interaction of shock wave with the R22 air column in later period.
图 4 B=0.01T时不同磁场方向对激波与R22气柱作用过程的影响
Figure 4. Numerical results of the interaction process of shock wave and R22 air column when B=0.01T
图 5 初始磁场沿y轴正方向时入射激波诱导射流产生过程
Figure 5. Generation process of jet induced by incident shock wave when initial magnetic field is along y axis
图 6 初始磁场沿x轴正方向时入射激波诱导射流产生过程
Figure 6. Generation process of jet induced by incident shock wave when initial magnetic field is along x axis
图 7 后期激波与R22气柱作用过程密度纹影
Figure 7. Numerical results of interaction process of shock wave with R22 air column in later period
图 8 初始磁场沿y轴正方向时磁压力及磁能量的分布(每幅子图中，左上为磁压力，左下为磁能量，中间和右侧分别为磁压力在x、y方向的分量)
Figure 8. Magnetic pressure and magnetic energy when initial magnetic field is along y axis (upper left: magnetic pressure; lower left: magnetic energy; middle: magnetic pressure along x axis; right: magnetic pressure along y axis)
图 9 初始磁场沿y轴正方向时的磁压力及磁能量分布
Figure 9. Distribution of magnetic pressure and magnetic energy when initial magnetic field is along y axis
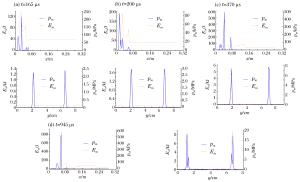
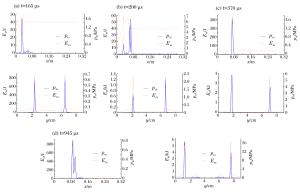
图 10 初始磁场沿x轴正方向时磁压力及磁能量分布(每幅子图中，左上为磁压力，左下为磁能量，中间和右侧分别为磁压力在x、y方向的分量)
Figure 10. Magnetic pressure and magnetic energy when initial magnetic field is along x axis (upper left: magnetic pressure; lower left: magnetic energy; middle: magnetic pressure along x axis; right: magnetic pressure along y axis)
图 11 初始磁场沿x轴正方向时边界处磁压力矢量图
Figure 11. Vector diagram of magnetic pressure on the interface when initial magnetic field is along x axis
图 12 初始磁场为x轴正方向时磁压力及磁能量分布
Figure 12. Distribution of magnetic pressure and magnetic energy when initial magnetic field is along x axis
表 1 气体参数
Table 1. Gas parameters used in this paper
气体 比热比 密度/(kg·m-3) 摩尔质量/(g·mol-1) 当地声速/(m·s-1) R22 1.185 3.69 86.468 183 Air 1.400 1.18 29.000 345 
下载: 导出CSV
-
[1] Meyer K A, Blewett P J. Numerical investigation of the stability of a shock-accelerated interface between two fluids[J]. Physics of Fluids, 1972, 15(5):753-759. doi: 10.1063/1.1693980 [2] Zhang Q, Sohn S I. An analytical nonlinear theory of Richtmyer-Meshkov instability[J]. Physics Letters A, 1996, 212(3):149-155. doi: 10.1016/0375-9601(96)00021-7 [3] Anuchina N N, Volkov V I, Gordeychuk V A, et al. Numerical simulations of Rayleigh-Taylor and Richtmyer-Meshkov instability using MAH-3 code[J]. Journal of Computational and Applied Mathematics, 2004, 168(1/2):11-20. http://cn.bing.com/academic/profile?id=faf4cdc7512f18529484c6b45fe5a4cc&encoded=0&v=paper_preview&mkt=zh-cn [4] Ruev G A, Fedorov A V, Fomin V M. Development of the Richtmyer-Meshkov instability upon interaction of a diffusion mixing layer of two gases with shock waves[J]. Journal of Applied Mechanics and Technical Physics, 2005, 46(3):307-314. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=33cb95fc5314ec07df6946d2ba77037c [5] Niederhaus J H J, Greenough J A, Oakley J G, et al. A computational parameter study for the three-dimensional shock-bubble interaction[J]. Journal of Fluid Mechanics, 2008, 594:85-124. http://cn.bing.com/academic/profile?id=412d738c3ad78e224720d2313a46ddb5&encoded=0&v=paper_preview&mkt=zh-cn [6] Thornber B, Drikakis D, Youngs D. Large-eddy simulation of multi-component compressible turbulent flows using high resolution methods[J]. Computers and Fluids, 2008, 37(7):867-876. doi: 10.1016/j.compfluid.2007.04.009 [7] Hejazialhosseini B, Rossinelli D, Bergdorf M, et al. High order finite volume methods on wavelet-adapted grids with local time-stepping on multicore architectures for the simulation of shock-bubble interactions.[J]. Journal of Computational Physics, 2010, 229(22):8364-8383. doi: 10.1016/j.jcp.2010.07.021 [8] Schilling O, Latini M. High-order weno simulations of three-dimensional reshocked Richtmyer-Meshkov instability to late times: Dynamics, dependence on initial conditions, and comparisons to experimental data[J]. Acta Mathematica Scientia, 2010, 30(2):595-620. doi: 10.1016/S0252-9602(10)60064-1 [9] Tian B, Shen W, Jiang S, et al. A global arbitrary Lagrangian-Eulerian method for stratified Richtmyer-Meshkov instability[J]. Computers and Fluids, 2011, 46(1):113-121. http://cn.bing.com/academic/profile?id=23c103f293bda4adebcd35feaf542796&encoded=0&v=paper_preview&mkt=zh-cn [10] Shankar S K, Kawai S, Lele S K. Two-dimensional viscous flow simulation of a shock accelerated heavy gas cylinder[J]. Physics of Fluids, 2011, 23(2):131. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=8036dad7385696611c022a99cb5bc7b7 [11] Bailie C, Mcfarland J A, Greenough J A, et al. Effect of incident shock wave strength on the decay of Richtmyer-Meshkov instability-introduced perturbations in the refracted shock wave[J]. Shock Waves, 2012, 22(6):511-519. doi: 10.1007/s00193-012-0382-y [12] Chandrasekhar S. Hydrodynamic and hydromagnetic stability[M]. Dover Publications, 1961. [13] Wheatley V, Pullin D I, Samtaney R. Stability of an impulsively accelerated density interface in magnetohydrodynamics[J]. Physical Review Letters, 2005, 95(12):125002. doi: 10.1103/PhysRevLett.95.125002 [14] Wheatley V, Samtaney R, Pullin D I. The magnetohydrodynamic Richtmyer-Meshkov instability: The transverse field case[C]//18th Australasian Fluid Mechanics Conference. Australasian Fluid Mechanics Society, 2012. [15] Khan M, Mandal L, Banerjee R, et al. Development of Richtmyer-Meshkov and Rayleigh-Taylor instability in presence of magnetic field[J]. Nuclear Instruments & Methods in Physics Research A, 2011, 653(1):2-6. http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_1101.3860 [16] Cao J, Wu Z, Ren H, et al. Effects of shear flow and transverse magnetic field on Richtmyer-Meshkov instability[J]. Physics of Plasmas, 2008, 15(4):445-514. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=c65ffb22c021910d193687d3d30e6647 [17] Shin M S, Stone J M, Snyder G F. The magnetohydrodynamics of shock-cloud interaction in three dimensions[J]. Astrophysical Journal, 2008, 680(1):336-348. doi: 10.1086/529160 [18] 李源, 罗喜胜.黏性、表面张力和磁场对Rayleigh-Taylor不稳定性气泡演化影响的理论分析[J].物理学报, 2014, 2(8):277-285. http://d.old.wanfangdata.com.cn/Periodical/wlxb201408037Li Yuan, Luo Xisheng. Theoretical analysis of effects of viscosity, surface tension, and magnetic field on the bubble evolution of Rayleigh-Taylor instability[J]. Acta Physica Sinica, 2014, 2(8):277-285. http://d.old.wanfangdata.com.cn/Periodical/wlxb201408037 [19] Saltzman J. An unsplit 3D upwind method for hyperbolic conservation laws[J]. Journal of Computational Physics, 1994, 115(1):153-168. doi: 10.1006/jcph.1994.1184 [20] Gardiner T A, Stone J M. An unsplit Godunov method for ideal MHD via constrained transport[J]. Journal of Computational Physics, 2005, 205(2):509-539. doi: 10.1016/j.jcp.2004.11.016 [21] Haas J, Sturtevant B. Interaction of weak shock waves with cylindrical and spherical gas inhomogeneities[J]. Journal of Fluid Mechanics, 1987, 181(1):41-76. http://cn.bing.com/academic/profile?id=f857b28c6f0747bace4c970ef14bb4aa&encoded=0&v=paper_preview&mkt=zh-cn [22] Chapman S, Cowling T G. The mathematical theory of non-uniform gases[M]. London: Cambridge University Press, 1970. [23] 沙莎, 陈志华, 薛大文.激波冲击R22重气柱所导致的射流与混合研究[J].物理学报, 2013, 62(14):144701. doi: 10.7498/aps.62.144701Sha Sha, Chen Zhihua, Xue Dawen. The generation of jet and mixing induced by the interaction of shock wave with R22 cylinder[J]. Acta Physica Sinica, 2013, 62(14):144701. doi: 10.7498/aps.62.144701 -
计量
- 文章访问数: 4335
- HTML全文浏览量: 1336
- PDF下载量: 215
- 被引次数: 0