Attenuation law of blasting induced ground vibrations based on equivalent path
-
摘要: 针对露天矿山台阶爆破地形和地质条件的复杂性, 分析了地形对爆破地震波传播路径的影响, 提出了等效路径及等效距离两个概念。同时考虑岩石波阻抗和岩体的完整性系数及最大一段装药量与炸药的定容爆热等因素的影响, 构建了露天台阶爆破地震波地表质点振速峰值随等效距离衰减的表达式。通过矿山爆破震动监测检验, 发现用该公式预测地表质点振速峰值, 能够适应实际地形和地质条件的变化, 预测结果的准确性显著高于萨氏公式, 表明该公式较好地反映了质点振速峰值沿等效路径衰减的基本规律, 为台阶爆破地震波质点振速峰值预测提供了一种新方法。Abstract: In this work, in view of the widely understood idea that topography and geological conditions are usually complicated and have a critical influence on the level of blast induced ground vibrations, we analyzed the effect of topography on the path through which seismic waves travel, introduced two concepts, the equivalent path and the equivalent distance, and established an equation for determining the surface peak particle velocity, taking into account of the effects of the maximum explosive charge quantity of a single initiation period, the explosion heat of the explosive product used, the acoustic impedance of the rock, and the integrity coefficient of the rock mass. A series of field seismic monitoring tests were carried out to determine the reliability of the equation. The result show that this equation can be used to describe the relationship between the peak particle velocity and the equivalent distance, and be applied under actual field topographical and geological conditions with a much higher accuracy than that of the Sardovsky's equation, proving the reliability of the equivalent distance based equation describing the attenuation basic patterns of seismic waves and possibility for use in field practice.
-
Key words:
- blasting /
- ground vibration /
- peak particle velocity /
- topography /
- equivalent distance
-
图 5 质点振速时程图示例
Figure 5. An example of the monitored seismogram of blast induced ground vibrations
图 6 爆破震动监测振动传感器的布置示例
Figure 6. An example of layout of geophones for monitoring of blast induced ground vibrations
图 7 置信度为95%时公式(6)的线性回归拟合结果
Figure 7. Fitted results of linear regression of the equation (6) with a confidence level of 95%
表 1 爆破地表质点振速峰值预测经验公式[9]
Table 1. Empirical equations for prediction of blast induced peak particle velocity
中国 美国 瑞典 英国 日本 印度 $v = K{\left( {\frac{{{Q^n}}}{R}} \right)^a}$ $v = K{\left( {R{Q^{ - n}}} \right)^a} $ $v = K\frac{{{Q^{1/2}}}}{{{R^{1/3}}}} $ $v = K\frac{{{Q^{1/2}}}}{R}$ $v = K\frac{{{Q^{3/4}}}}{{{R^2}}}$ $v = K{\left( {\frac{Q}{{{R^{\left. {2/3} \right)}}}}} \right)^a}$ 
下载: 导出CSV
表 2 岩石与岩体的相关参数
Table 2. Parameters of rock and rock mass
岩种 岩石密度ρ/(g·cm-3) 岩石波速c/(km·s-1) 岩体波速c′/(km·s-1) 岩体完整性系数η Fe1 Fe11 3.526 5.33 3.35 0.395 Fe12 3.526 5.33 4.13 0.600 Fe13 3.526 5.33 4.62 0.750 Fe2 Fe21 3.461 5.13 2.29 0.200 Fe22 3.461 5.13 3.15 0.376 SS SS1 2.577 5.01 2.74 0.300 SS2 2.577 5.01 3.71 0.550 SS3 2.577 5.01 4.58 0.836 SS4 2.577 5.01 4.75 0.900
下载: 导出CSV
表 3 质点振速峰值现场监测结果
Table 3. Recorded peak particle velocity (vmax) from field seismic monitoring
测点序号 最大单段装药量Q/kg 分段等效距离Ri/m 等效距离
∑Ri/m质点振速峰值
v/(cm·s-1)主频
f/Hz乳化 铵油 Fe1 Fe2 SS 1 540 360 135.99 0 153.25 289.24 1.09 4.88 3 540 360 156.58 0 478.00 634.58 0.29 11.72 4 0 750 0 0 149.86 149.86 2.74 40.04 5 0 750 0 0 220.59 220.59 1.61 18.55 6 0 750 129.00 67.61 452.24 648.85 0.13 12.70 7 450 0 0 258.92 98.2 357.12 0.60 26.37 8 450 0 0 261.76 27.71 289.47 0.97 10.74 9 450 0 34.29 140.71 123.45 298.45 0.8 4.88 10 270 450 0 0 553.66 553.66 0.43 33.20 11 270 450 0 0 553.66 553.66 0.49 33.20 12 270 450 0 0 741.59 741.59 0.25 12.70 13 0 450 70.71 0 45.16 115.87 3.15 34.18 14 0 450 70.71 0 45.16 115.87 3.15 34.18 15 0 450 72.04 232.42 148.95 453.41 0.20 16.60 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 48 0 420 7.68 89.09 120.22 216.99 1.92 35.16
下载: 导出CSV
表 4 萨氏公式回归分析结果
Table 4. Calculated results of linear regression of peak particle velocity with Sardofsky's equation
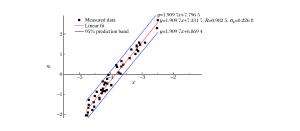
参数 水平距离 空间距离 K 704.226 5 702.540 0 α 1.938 4 1.927 4 相关系数R 0.953 6 0.951 5 剩余均方差σR 0.366 4 0.374 3
下载: 导出CSV
表 5 等效距离公式及萨氏公式的质点振速峰值预测值与实测值的比较
Table 5. Relative error ε and the average relative error of the equivalent distance equation and Sardovsky's equationto the recorded data
序号 实测值/(cm·s-1) 萨氏公式(水平距离) 萨氏公式(空间距离) 等效距离公式 预测值/(cm·s-1) 相对误差ε/% 预测值/(cm·s-1) 相对误差ε/% 预测值/(cm·s-1) 相对误差ε/% 1 1.09 1.50 37.96 1.54 41.24 1.19 9.56 2 0.58 0.75 29.96 0.78 34.31 0.76 31.71 3 0.29 0.26 11.07 0.27 7.02 0.37 28.50 4 2.74 3.45 26.01 3.53 28.80 3.32 21.16 5 1.61 1.17 27.49 1.18 26.62 1.59 1.45 6 0.13 0.19 46.81 0.20 52.57 0.18 35.09 7 0.60 0.49 18.06 0.43 28.40 0.50 16.85 8 0.97 0.75 23.17 0.66 31.94 0.64 33.94 9 0.80 0.60 24.51 0.63 21.49 0.60 25.57 10 0.43 0.57 33.35 0.60 38.79 0.46 6.17 11 0.49 0.57 17.03 0.60 21.79 0.46 6.83 12 0.25 0.14 44.44 0.15 41.92 0.26 4.51 13 3.15 3.67 16.47 3.72 18.21 3.92 24.48 24 3.15 3.67 16.47 3.72 18.21 3.92 24.48 15 0.20 0.27 32.55 0.27 35.72 0.27 35.43 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 48 1.92 1.11 42.44 1.11 42.40 1.42 26.13 平均误差ε′/% 32.0 32.69 19.14
下载: 导出CSV
-
[1] 中华人民共和国国家标准编写组.爆破安全规程: GB 6722-2014[S].北京: 中国标准出版社, 2014. [2] Reza N.Prediction of ground vibration level induced by blasting at different rock units[J].International Journal of Rock Mechanics and Mining Sciences, 2011, 48(6):899-908. doi: 10.1016/j.ijrmms.2011.04.014 [3] 张继春.三峡工程基岩爆破振动特性的试验研究[J].爆炸与冲击, 2001, 21(2):131-137. doi: 10.3321/j.issn:1001-1455.2001.02.009Zhang Jichun.Vibration characteristics of blasting in bed rock mass at Sanxia Project[J].Explosion and Shock Waves, 2001, 21(2):131-137. doi: 10.3321/j.issn:1001-1455.2001.02.009 [4] 郭学彬, 肖正学, 张志呈.爆破振动作用的坡面效应[J].岩石力学与工程学报, 2001, 20(1):83-87. doi: 10.3321/j.issn:1000-6915.2001.01.019Guo Xuebin, Xiao Zhengxue, Zhang Zhicheng.Slope effect of blasting vibration[J].Chinese Journal of Rock Mechanics and Engineering, 2001, 20(1):83-87. doi: 10.3321/j.issn:1000-6915.2001.01.019 [5] 朱传统, 刘宏根, 梅锦煜.地震波参数沿边坡坡面传播规律公式的选择[J].爆破, 1988, 10(2):30-31. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK000001125919Zhu Chuantong, Liu Honggen, Mei Jinyu.Equation selection of the transmission rule of seismic wave parameters along slope surface[J].Blasting, 1988, 10(2):30-31. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK000001125919 [6] Nguyena K V, Gatmiri B.Evaluation of seismic ground motion inducedbytopographic irregularity[J].Soil Dynamics and Earthquake Engineering, 2007, 27(2):183-188. http://www.sciencedirect.com/science/article/pii/S026772610600114X [7] 宋光明, 陈寿如, 史秀志, 等.露天矿边坡爆破振动监测与评价方法的研究[J].有色金属(矿山部分), 2000(4):24-27. doi: 10.3969/j.issn.1671-4172.2000.04.007Song Guangming, Chen Shouru, Shi Xiuzhi, et al.Research on the methods of measurement and evaluation of blasting vibration in open-pit mines[J].Nonferrous Metal (Mining), 2000(4):24-27. doi: 10.3969/j.issn.1671-4172.2000.04.007 [8] Guillaume G, Picaut J, Dutilleux G, et al.Time-domain impedance equationtion for transmission line matrix modelling of outdoor sound propagation[J].Journal of Sound and Vibration, 2011, 330(26):6467-6481. doi: 10.1016/j.jsv.2011.08.004 [9] 饶运章, 汪弘.爆破振动速度衰减规律的多元线性回归分析[J].金属矿山, 2013, 450(12):46-47;51. http://d.old.wanfangdata.com.cn/Periodical/jsks201312014Rao Yunzhang, Wang Hong.Multiple regression linear analysis on attenuation equation of blasting vibration velocity[J].Metal Mines, 2013, 450(12):46-47;51. http://d.old.wanfangdata.com.cn/Periodical/jsks201312014 [10] 谭文辉, 璩世杰, 毛市龙, 等.边坡爆破振动高程效应分析[J].岩土工程学报, 2010, 32(4):619-623. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK201001261659Tan Wenhui, Qu Shijie, Mao Shilong, et al.Analysis on altitude effect ofblasting vibration in slopes[J].Chinese Journal of Geotechnical Engineering, 2010, 32(4):619-623. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK201001261659 [11] 张华, 高富强, 杨军, 等.深凹露天爆破震动速度衰减规律实验研究.兵工学报, 2010, 31(增刊1):275-278. http://d.old.wanfangdata.com.cn/Conference/7151832Zhang Hua, Gao Fuqiang, Yang Jun, et al.Experimental studies on blasting vibration velocity attenuation lawin deep openpit mining.Acta Armamentarii, 2010, 31(suppl 1):275-278. http://d.old.wanfangdata.com.cn/Conference/7151832 [12] 刘美山, 吴从清, 张正宇.小湾水电站高边坡爆破震动安全判据试验研究[J].长江科学院院报, 2007, 24(1):40-43. doi: 10.3969/j.issn.1001-5485.2007.01.011Liu Meishan, Wu Congqing, Zhang Zhengyu.Experimentation on judging standard of blasting vibration safetyin high slope excavation of Xiaowan Hydropower Station[J].Journal of Yangtze River Scientif ic Research Institute, 2007, 24(1):40-43. doi: 10.3969/j.issn.1001-5485.2007.01.011 [13] 裴来政.金堆城露天矿高边坡爆破震动监测与分析[J].爆破, 2006, 23(4):82-85. http://d.old.wanfangdata.com.cn/Periodical/bp200604023Pei Laizheng.Observation and analysis of blasting vibration to the high slope of Jinduicheng open-pit mine[J].Blasting, 2006, 23(4):82-85. http://d.old.wanfangdata.com.cn/Periodical/bp200604023 -
计量
- 文章访问数: 4621
- HTML全文浏览量: 1428
- PDF下载量: 298
- 被引次数: 0