A calculation method of the peak pressure on borehole wall for low decoupling coefficient charge blasting
-
摘要: 基于轮廓爆破孔壁压力峰值计算方法的相关研究,充分考虑空气冲击波的传播与爆轰产物膨胀的过程,理论分析了小不耦合系数装药爆破过程中空气冲击波与炮孔壁的相互作用,建立了三维空气介质径向不耦合装药单孔爆破有限元模型,研究了工程爆破中常用的多种小不耦合系数装药组合工况下,炸药单点起爆后的炮孔壁压力峰值,并获得了相应工况下的孔壁压力峰值较爆生气体准静态等熵膨胀压力的压力增大倍数。结果表明:小不耦合系数装药爆破过程中,爆轰产物参数会对空气冲击波波后物质参数产生显著影响,揭示了小不耦合系数装药爆破与轮廓爆破在孔壁压力峰值计算方法上的本质差异;柱状装药结构爆轰波沿轴向传播使得空气冲击波撞击炮孔壁时存在叠加效应,孔壁压力峰值也相应增大,通过统计分析不同炸药类型、不同岩石类型工况下压力增大倍数与不耦合系数的关系,发现压力增大倍数随不耦合系数的增大近似呈线性增长;基于理论推导结果及常用爆破孔壁压力峰值计算形式,综合考虑炸药性能、孔壁岩石介质条件、不耦合装药系数对空气冲击波撞击炮孔壁后压力增大倍数的影响,提出了不耦合系数较小时爆破孔壁压力峰值计算方法。Abstract: The peak pressure on a borehole wall is an important parameter for the analysis of rock blasting rupture and the non-fluid solid coupling explosion impact dynamic response. Based on the relevant research of calculation methods for the peak pressure on the borehole wall for contour blasting, the interaction between the air shock waves and the borehole wall during low decoupling coefficient charge blasting was theoretically analyzed, and the influencing factors of pressure increase ratio were obtained by fully considering the process of air shock wave propagation and detonation product expansion. The parameters of detonation products were used instead of those of shock wave products in theoretical derivation. The single-hole finite element blasting model with radial decoupling charge for air medium was established, and the peak pressure of the borehole wall after single-point detonation of explosives was studied under the combination conditions of multiple low decoupling coefficient charge structure commonly used in engineering blasting. Moreover, the pressure increase ratio which was the ratio of the peak pressure on the borehole wall to the quasi-static isentropic expansion pressure of explosion gas was obtained under the corresponding conditions. The results show that in the process of explosive blasting with a low decoupling coefficient, there is no separation of air shock waves and detonation products, the parameters of the detonation products have a significant effect on the parameters after air shock waves, which in turn affects the interaction between the air shock waves and the borehole wall. It reveals the essential difference between the calculation methods for the peak pressure on the borehole wall in low decoupling coefficient charge blasting and contour blasting. In addition, the propagation of the axial detonation wave in the cylindrical charge structure causes a superposition effect when the air shock wave impacts the borehole wall, and the peak pressure increases accordingly. Through statistical analysis of the relationship between the pressure increase ratio and the decoupling coefficient under different explosive types and different rock types, it is found that the pressure increase ratio increases approximately linearly with the increase of the decoupling coefficient. Based on the the results of theoretical derivation and the commonly used calculation methods for the peak pressure on the borehole wall, a method for calculating the peak pressure on the borehole wall was proposed for low decoupling coefficient charge blasting by considering the effects of explosive characteristics, medium conditions of the borehole wall, and decoupling coefficient on the pressure increase ratio after the air shock wave colliding with the borehole wall.
-
Key words:
- decoupling charge /
- explosion pressure /
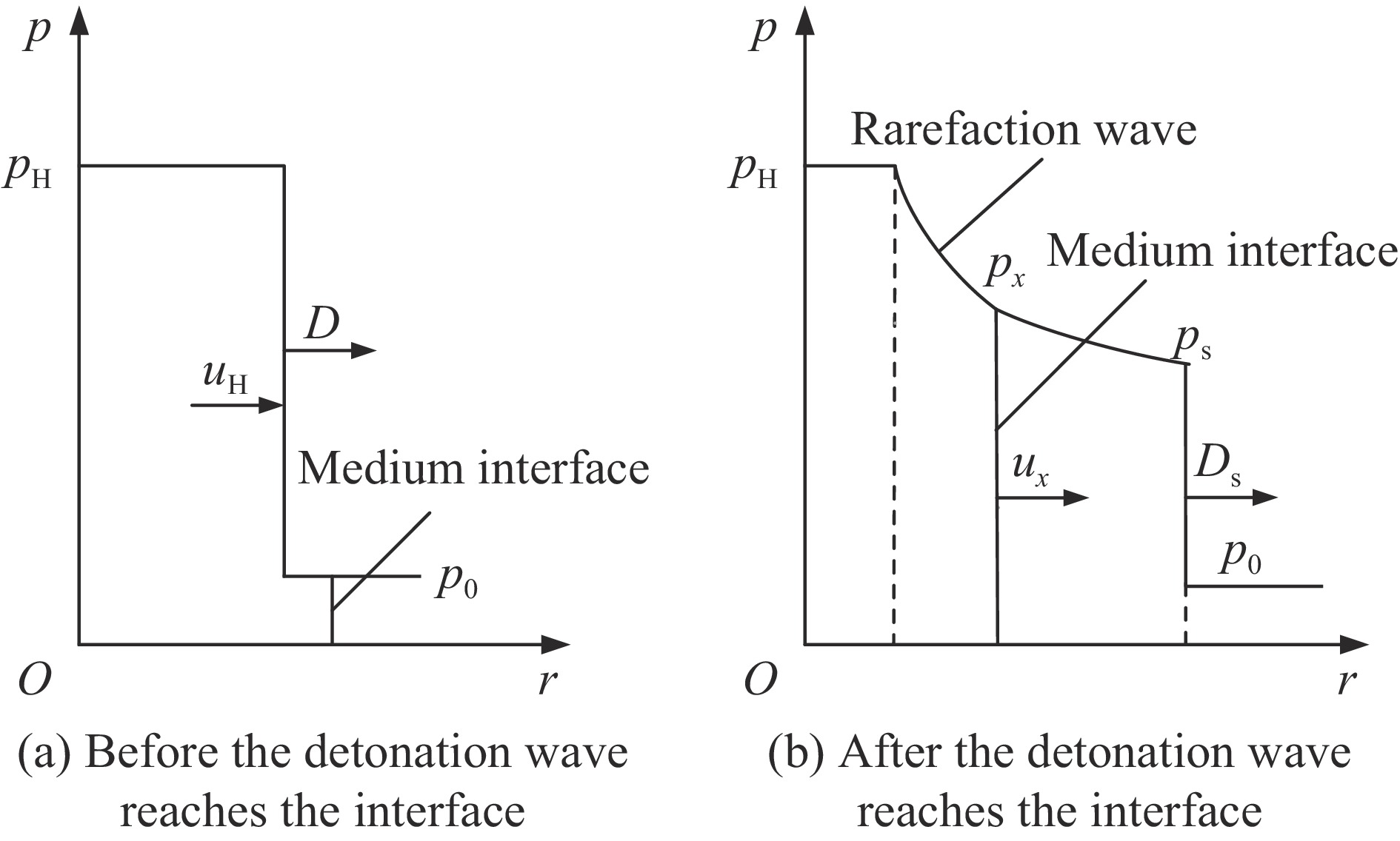
- shock wave /
- pressure increase ratio
-
表 1 三种典型岩石的物理力学参数
Table 1. Physical and mechanical parameters of three typical rocks
岩石 密度/(kg·m−3) 泊松比 弹性模量/GPa 屈服应力/MPa 切线模量/GPa 粉砂岩 2170 0.25 6.70 39.20 0.6 石灰岩 2600 0.25 32.50 72.90 3.0 花岗岩 2700 0.24 68.00 150.00 7.0 注:Cowper-Symonds参数C=2.5 s−1,Cowper-Symonds参数P=4.0。 表 2 两种常用炸药的计算参数
Table 2. Calculation parameters of two commonly used explosives
表 3 乳化炸药作用下空气冲击波透射压力与入射压力的比值
Table 3. Transmission-to-incident pressure ratio of air blast wave induced by emulsion explosive
装药条件 不耦合系数 p10/MPa 粉砂岩 石灰岩 花岗岩 平均值 px2/MPa px2/p10 px2/MPa px2/p10 px2/MPa px2/p10 px2/MPa px2/p10 90/80 1.13 1283 3000 2.34 4260 3.32 4500 3.51 3920 3.06 110/90 1.22 780 2331 2.99 3083 3.95 3524 4.52 2979 3.82 76/60 1.27 630 2080 3.30 2610 4.15 2820 4.48 2503 3.98 90/70 1.29 576 2030 3.53 2870 4.99 2800 4.86 2567 4.46 110/80 1.38 385 1577 4.10 2297 5.97 2334 6.07 2069 5.38 90/60 1.50 228 1320 5.78 1860 8.15 1810 7.93 1663 7.29 表 4 铵油炸药作用下空气冲击波透射压力与入射压力比值
Table 4. Transmission-to-incident pressure ratio of air blast wave induced by ANFO explosive
装药条件 不耦合系数 p10/MPa 粉砂岩 石灰岩 花岗岩 平均值 px2/MPa px2/p10 px2/MPa px2/p10 px2/MPa px2/p10 px2/MPa px2/p10 90/80 1.13 494 2740 5.54 3440 6.96 3570 7.22 3250 6.57 110/90 1.22 301 2049 6.81 2756 9.17 2893 9.62 2566 8.53 76/60 1.27 243 1710 7.04 2215 9.12 2402 9.88 2109 8.68 90/70 1.29 222 1630 7.35 2430 10.95 2340 10.55 2133 9.61 110/80 1.38 148 1530 10.32 1837 12.38 2098 14.14 1822 12.28 90/60 1.50 88 1090 12.39 1370 15.57 1450 16.48 1303 14.81 表 5 压力增大倍数n′
Table 5. Pressure increase ratio n′
装药条件 不耦合系数 乳化炸药 铵油炸药 粉砂岩 石灰岩与花岗岩平均值 粉砂岩 石灰岩与花岗岩平均值 90/80 1.13 2.34 3.42 5.54 7.09 110/90 1.22 2.99 4.24 6.81 9.40 76/60 1.27 3.30 4.32 7.04 9.50 90/70 1.29 3.53 4.93 7.35 10.75 110/80 1.38 4.10 6.02 10.32 13.26 90/60 1.50 5.78 8.04 12.39 16.03 -
[1] 刘云川, 汪旭光, 刘连生, 等. 不耦合装药条件下炮孔初始压力计算的能量方法 [J]. 中国矿业, 2009, 18(6): 104–107, 110. DOI: 10.3969/j.issn.1004-4051.2009.06.031.LIU Y C, WANG X G, LIU L S, et al. An energy method for calculate borehole pressure under decoupled charging [J]. China Mining Magazine, 2009, 18(6): 104–107, 110. DOI: 10.3969/j.issn.1004-4051.2009.06.031. [2] 梁为民, LIU H Y, 周丰峻. 不耦合装药结构对岩石爆破的影响 [J]. 北京理工大学学报, 2012, 32(12): 1215–1218, 1228. DOI: 10.3969/j.issn.1001-0645.2012.12.002.LIANG W M, LIU H Y, ZHOU F J. Influence of air-decoupling charge on rock blasting [J]. Transactions of Beijing Institute of Technology, 2012, 32(12): 1215–1218, 1228. DOI: 10.3969/j.issn.1001-0645.2012.12.002. [3] 朱瑞赓, 王雪峰. 不耦合装药爆破孔壁压力的计算(一) [J]. 爆破, 1990(3): 1–4.ZHU R G, WANG X F. Calculation of blasthole wall pressure of de-coupled charges [J]. Blasting, 1990(3): 1–4. [4] 万元林, 王树仁. 关于空气不偶合装药初始冲击压力计算的分析 [J]. 爆破, 2001, 18(1): 13–15. DOI: 10.3963/j.issn.1001-487X.2001.01.004.WAN Y L, WANG S R. Analyse of impact pressure about de-coupling charge [J]. Blasting, 2001, 18(1): 13–15. DOI: 10.3963/j.issn.1001-487X.2001.01.004. [5] 李玉民, 倪芝芳. 不耦合装药岩石冲击波参量的极曲线方法 [J]. 岩石力学与工程学报, 1998, 17(1): 76–80. DOI: 10.3321/j.issn:1000-6915.1998.01.011.LI Y M, NI Z F. The polar curve method to calculate the parameters of shock wave in rock blasting with uncoupled charge [J]. Chinese Journal of Rock Mechanics and Engineering, 1998, 17(1): 76–80. DOI: 10.3321/j.issn:1000-6915.1998.01.011. [6] 朱振海, 曲广建, 孙强, 等. 不耦合装药爆炸应力场的动光弹研究 [J]. 爆炸与冲击, 1991, 11(3): 252–257.ZHU Z H, QU G J, SUN Q, et al. Dynamic photoelastic investigation of the action of decouple [J]. Explosion and Shock Waves, 1991, 11(3): 252–257. [7] FELDGUN V R, KARINSKI Y S, YANKELEVSKY D Z. Experimental simulation of blast loading on structural elements using rarefaction waves-theoretical analysis [J]. International Journal of Impact Engineering, 2017, 102: 86–101. DOI: 10.1016/j.ijimpeng.2016.12.010. [8] SAHARAN M R, MITRI H S. Numerical procedure for dynamic simulation of discrete fractures due to blasting [J]. Rock Mechanics and Rock Engineering, 2008, 41(5): 641–670. DOI: 10.1007/s00603-007-0136-9. [9] YILMAZ O, UNLU T. Three dimensional numerical rock damage analysis under blasting load [J]. Tunnelling and Underground Space Technology, 2013, 38: 266–278. DOI: 10.1016/j.tust.2013.07.007. [10] YI C P, JOHANSSON D, GREBERG J. Effects of in-situ stresses on the fracturing of rock by blasting [J]. Computers and Geotechnics, 2018, 104: 321–330. DOI: 10.1016/j.compgeo.2017.12.004. [11] HENRYCH J. The dynamics of explosion and its use [M]. Amsterdam: Elsevier, 1979. [12] 钮强. 岩石爆破机理[M]. 沈阳: 东北工学院出版社, 1990: 18−19. [13] 陈明, 刘涛, 叶志伟, 等. 轮廓爆破孔壁压力峰值计算方法 [J]. 爆炸与冲击, 2019, 39(6): 064202. DOI: 10.11883/bzycj-2018-0171.CHEN M, LIU T, YE Z W, et al. Calculation methods for peak pressure on borehole wall of contour blasting [J]. Explosion and Shock Waves, 2019, 39(6): 064202. DOI: 10.11883/bzycj-2018-0171. [14] 罗兴柏, 张玉令, 丁玉奎. 爆炸及其防护简明教程[M]. 北京: 国防工业出版社, 2016: 254−259. [15] 宁建国, 王成, 马天宝. 爆炸与冲击动力学[M]. 北京: 国防工业出版社, 2010: 110−112. [16] 周霖, 张向荣. 炸药爆炸能量转换原理及应用[M]. 北京: 国防工业出版社, 2015: 136−141. [17] Livermore Software Technology Corporation. LS-DYNA theoretical manual [M]. California: Livermore Software Technology Corporation, 2003: 1012−1013. [18] 夏祥, 李海波, 李俊如, 等. 岭澳核电站二期工程基岩爆破安全阈值分析 [J]. 岩土力学, 2008, 29(11): 2945–2951, 2956. DOI: 10.3969/j.issn.1000-7598.2008.11.010.XIA X, LI H B, LI J R, et al. Research on vibration safety threshold for rock under blasting excavation [J]. Rock and Soil Mechanics, 2008, 29(11): 2945–2951, 2956. DOI: 10.3969/j.issn.1000-7598.2008.11.010. [19] 刘军. 岩体在冲击载荷作用下的各向异性损伤模型及其应用 [J]. 岩石力学与工程学报, 2004, 23(4): 635–640. DOI: 10.3321/j.issn:1000-6915.2004.04.020.LIU J. Anisotropic damage model and its application to rock materials under impact load [J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(4): 635–640. DOI: 10.3321/j.issn:1000-6915.2004.04.020. -







 下载:
下载: