多孔铁电陶瓷冲击压缩响应与损伤演化的离散元数值模拟

蒋招绣; 高光发; 王永刚

doi:10.11883/bzycj-2019-0410

多孔铁电陶瓷冲击压缩响应与损伤演化的离散元数值模拟

doi: 10.11883/bzycj-2019-0410

蒋招绣^{1, 2,},
高光发¹,
王永刚^2, ,

1.
南京理工大学机械工程学院，江苏南京 210094
2.
宁波大学冲击与安全工程教育部重点实验室，浙江宁波 315211

基金项目: 国家自然科学基金（11972202，11772160）；冲击与安全工程教育重点实验室开放课题（Cj201903）；爆炸科学与技术国家重点实验室基金（KFJJ18-01M）

详细信息

作者简介:
蒋招绣（1986－　），男，博士，jiangzhaoxiu@njust.edu.cn

通讯作者:
王永刚（1976－　），男，博士，教授，wangyonggang@nbu.edu.cn

中图分类号: O347.4
计量
- 文章访问数: 3858
- HTML全文浏览量: 1114
- PDF下载量: 63
- 被引次数: 0
出版历程
- 收稿日期: 2019-10-23
- 修回日期: 2019-11-24
- 刊出日期: 2020-05-01

Discrete element simulation on dynamic response and damage evolution in porous ferroelectric ceramics under shock compression

JIANG Zhaoxiu^{1, 2
,},
GAO Guangfa¹,
WANG Yonggang^{2
, ,}

1.
School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China
2.
Key Laboratory of Impact and Safety Engineering, Ministry of Education of China, Ningbo University, Ningbo 315211, Zhejiang, China

摘要

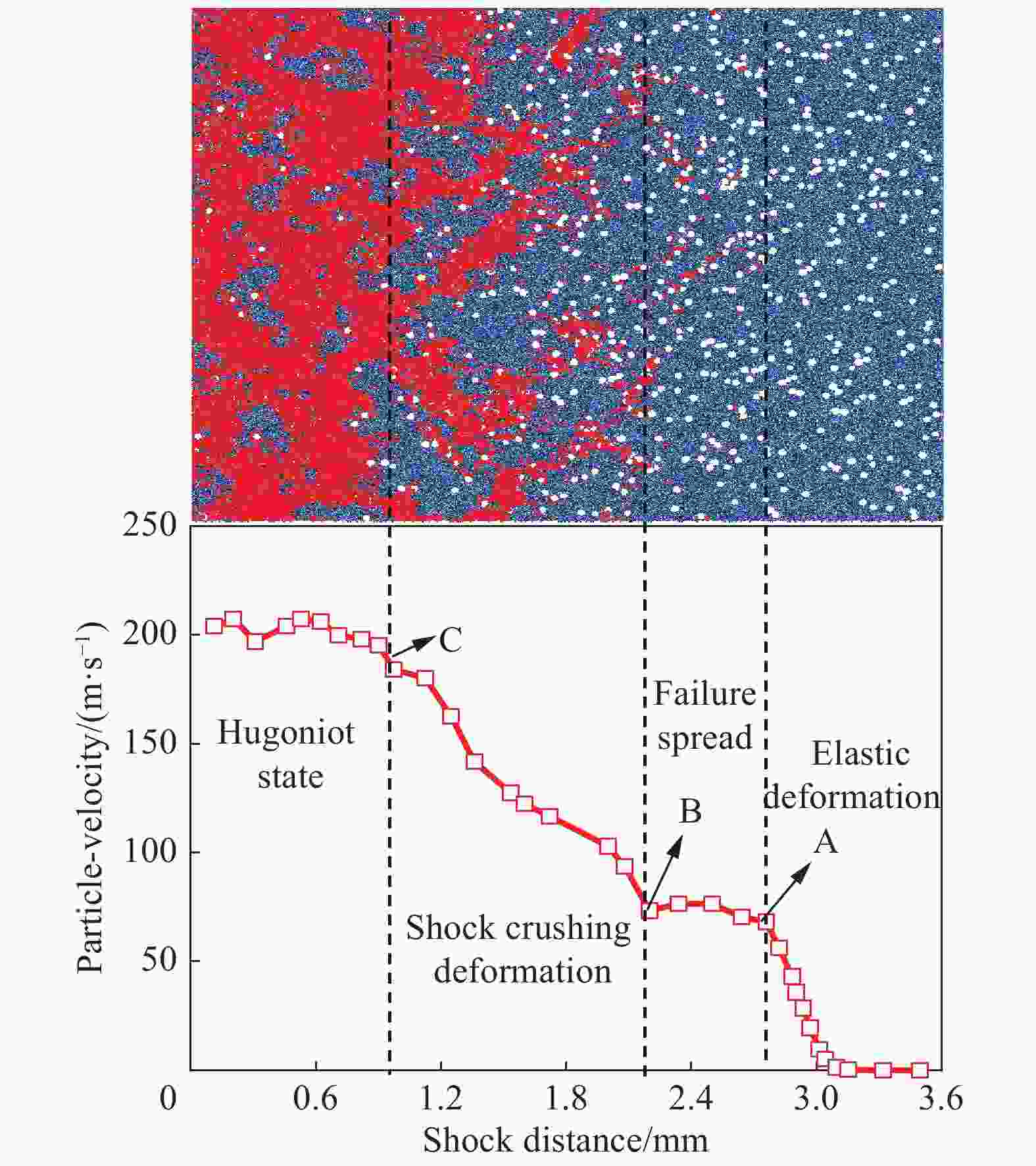
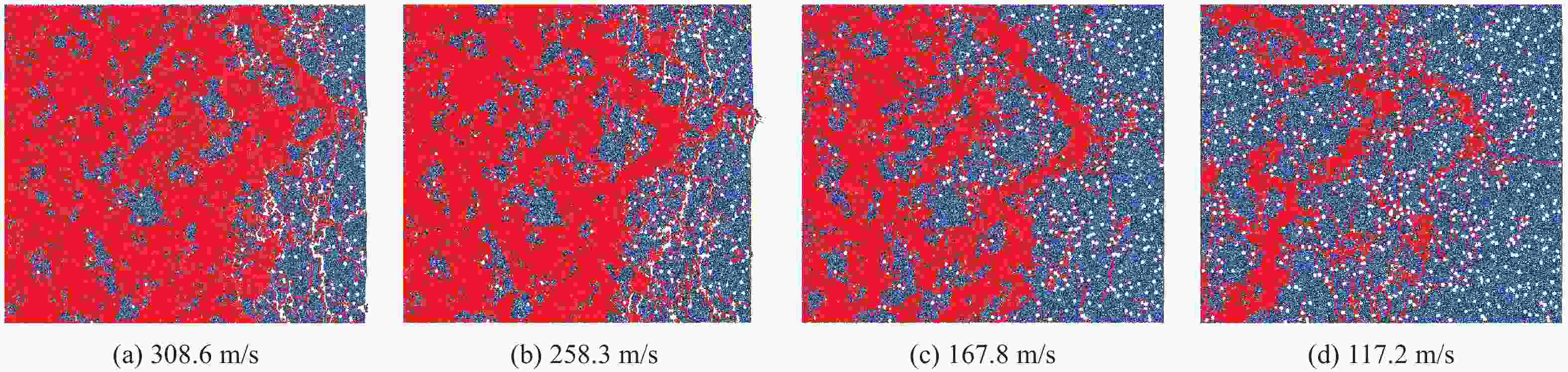
摘要: 采用flat-joint粘结模型，建立多孔铁电陶瓷在一维应变冲击压缩下的PFC (particle flow code)颗粒流离散元模型，通过数值模拟再现了平板撞击实验中实测的自由面速度剖面历史，并揭示了多孔铁电陶瓷在冲击压缩下的响应过程与损伤演化机制。多孔铁电陶瓷在冲击压缩下的响应过程可分4个阶段：弹性变形、失效蔓延、冲击压溃变形、冲击Hugoniot平衡状态；其中，失效蔓延的内在机制是由剪切裂纹的成核与增长，而冲击压溃变形的主要机制是孔洞的塌缩以及层状剪切裂纹的形成与扩展；冲击速度与孔隙率对铁电陶瓷的响应有显著的影响，Hugoniot弹性极限强烈依赖于孔隙率，但与冲击速度的大小无关，宏观损伤累积随着冲击速度和孔隙率的增加而增加。
- 铁电陶瓷 /
- 离散元 /
- 损伤演化 /
- 动态响应
Abstract: Based on the flat-joint bonding model, the PFC (particle flow code) particle flow discrete model of porous ferroelectric ceramics under one-dimensional strain shock compression was established. The free-surface velocity profiles measured in plate impact experiments have been well reproduced by the discrete element simulation, and the response process and damage evolution mechanism of porous ferroelectric ceramics under shock compression were revealed. The response process of porous ferroelectric ceramics under shock compression can be divided into four stages: elastic deformation, failure spread, shock crushing deformation and shock Hugoniot equilibrium state. The mechanism of failure spread is the nucleation and growth of shear cracks. The main mechanism of shock crushing deformation is the formation and propagation of layered shear cracks and the collapse of voids. The impact velocity and porosity have significant effects on the dynamic response and damage evolution of porous ferroelectric ceramics. The Hugoniot elastic limit strongly depends on porosity and is not affected by impact velocity. The damage accumulation increases with the increase of impact velocity and porosity.
- ferroelectric ceramic /
- discrete element /
- damage evolution /
- dynamic response

HTML全文

图 1 flat-joint接触模型几何示意图^[17]

Figure 1. The schematic diagram of flat-joint contact model^[17]

下载: 全尺寸图片幻灯片

图 2 离散元宏观模型

Figure 2. The macroscopic model for discrete element

下载: 全尺寸图片幻灯片

图 3 多孔未极化PZT95/5铁电陶瓷SEM照片

Figure 3. SEM photograph of porous unpoled PZT95/5 ferroelectric ceramics

下载: 全尺寸图片幻灯片

图 4 实验与模拟自由面速度剖面

Figure 4. Free surface velocity profiles between experiment and simulation

下载: 全尺寸图片幻灯片

图 5 波剖面粒子速度与损伤分布

Figure 5. Particle-velocity profiles anddamage distribution

下载: 全尺寸图片幻灯片

图 6 不同时刻细观损伤分布

Figure 6. Microscopic damage distribution at different times

下载: 全尺寸图片幻灯片

图 7 不同冲击速度的自由面速度剖面

Figure 7. Free surface velocity profiles at different impact velocities

下载: 全尺寸图片幻灯片

图 8 损伤度与冲击速度的关系

Figure 8. Relation of damage degree to impact velocity

下载: 全尺寸图片幻灯片

图 9 不同冲击速度下Hugoniot平衡状态时试样的损伤分布

Figure 9. Damage distribution in equilibrium Hugoniot states at different impact velocities

下载: 全尺寸图片幻灯片

图 10 不同孔隙率试样的自由面速度剖面

Figure 10. Free surface velocity profiles of different porosity samples

下载: 全尺寸图片幻灯片

图 11 不同孔隙率试样的损伤分布

Figure 11. Damage distribution of different porosity samples

下载: 全尺寸图片幻灯片

表 1 实验条件

Table 1. Experimental conditions

样品	密度/(g·cm⁻³)	孔隙率/%	试样厚度/mm	飞片厚度/mm	冲击速度/(m·s⁻¹)
PZT1#1	7.440	6.96	3.63	4.02	249.4
PZT2#1	7.060	11.75	3.58	3.98	254.8
PZT3#1	6.670	16.56	3.62	4.06	308.6
PZT3#2	6.800	14.99	3.54	4.04	258.3
PZT3#3	6.810	14.89	3.60	4.08	167.8
PZT3#4	6.740	15.88	3.58	3.94	117.2

下载: 导出CSV

表 2 模型中主要参数

Table 2. The main parameters in model

材料	密度/(g·cm⁻³)	弹性模量/GPa	泊松比	法向拉伸强度/MPa	内聚力强度/MPa	摩擦角/（°）
试样	8.000	88.0	0.21	1 200.0	600.0	18.0
飞片	8.900	110.0	0.35

下载: 导出CSV

参考文献(24)

[1]	TUTTLE B A, YANG P, GIESKE J H. Pressure-induced phase transformation of controlled-porosity Pb(Zr_0.95Ti_0.05)O₃ ceramics [J]. Journal of the American Ceramic Society, 2001, 84(6): 1260–1264. DOI: 10.1111/j.1151-2916.2001.tb00826.x.
[2]	FENG N, NIE H, CHEN X, et al. Depoling of porous Pb_0.99(Zr_0.95Ti_0.05)_0.98Nb_0.02O₃ ferroelectric ceramics under shock wave load [J]. Current Applied Physics, 2010, 10(6): 1387–1390. DOI: 10.1016/j.cap.2010.04.012.
[3]	李成华, 蒋招绣, 王永刚, 等. 高应变率下多孔未极化PZT95/5铁电陶瓷的非线性力学为 [J]. 爆炸与冲击, 2018, 38(4): 707–715. DOI: 10.11883/bzycj-2016-0329. LI C H, JIANG Z X, WANG Y G, et al. Nonlinear mechanical response of PZT95/5 ferroelectric ceramics under high strain rate loading [J]. Explosion and Shock Waves, 2018, 38(4): 707–715. DOI: 10.11883/bzycj-2016-0329.
[4]	刘高旻, 刘雨生, 张毅, 等. PZT铁电陶瓷及其在脉冲能源中的应用 [J]. 材料导报, 2006, 20(6): 74–77. DOI: 10.3321/j.issn:1005-023X.2006.06.020. LIU G M, LIU Y S, ZHANG Y, et al. PZT ferroelectric ceramic for shock driver pulsed supply [J]. Materials Reports, 2006, 20(6): 74–77. DOI: 10.3321/j.issn:1005-023X.2006.06.020.
[5]	SHKURATOV S I, BAIRD J, ANTIPOV V G, et al. Depolarization mechanisms of PbZr_0.52Ti_0.48O₃ and PbZr_0.95Ti_0.05O₃ poled ferroelectrics under high strain rate loading [J]. Applied Physics Letters, 2014, 104(21): 212901. DOI: 10.1063/1.4879545.
[6]	DUNGAN R H, STORZ L J. Relation between chemical, mechanical, and electrical properties of Nb₂O₅-Modified-95Mol% PbZrO₃-5Mol% PbTiO₃ [J]. Journal of the American Ceramic Society, 1985, 68(10): 530–533. DOI: 10.1111/j.1151-2916.1985.tb11518.x.
[7]	喻寅, 王文强, 杨佳, 等. 多孔脆性介质冲击波压缩破坏的细观机理和图像 [J]. 物理学报, 2012, 61(4): 48103. DOI: 10.7498/aps.61.048103. YU Y, WANG W Q, YANG J, et al. Mesoscopic picture of fracture in porous brittle material under shock wave compression [J]. Acta Physica Sinica, 2012, 61(4): 48103. DOI: 10.7498/aps.61.048103.
[8]	SETCHELL R E. Shock wave compression of the ferroelectric ceramic Pb_0.99(Zr_0.95Ti_0.05)_0.9-Nb_0.02O₃: microstructural effects [J]. Journal of Applied Physics, 2007, 101: 053525. DOI: 10.1063/1.2697428.
[9]	RASORENOV S V, KANEL G I. The fracture of glass under high-pressure impulsive loading [J]. High Pressure Research, 1991(6): 225–232. DOI: 10.1080/08957959108202508.
[10]	GRADY D E. Dynamic failure in brittle solids [R]. Nasa Sti/recon Technical Report N, 1994: 95.
[11]	SETCHELL R E. Shock wave compression of the ferroelectric ceramic Pb_0.99(Zr_0.95Ti_0.05)_0.9-Nb_0.02O₃: Hugoniot states and constitutive mechanical properties [J]. Journal of Applied Physics, 2003, 94(1): 1519–1525. DOI: 10.1063/1.1578526.
[12]	赵铮, 李晓杰, 陶钢. 冲击载荷下孔隙塌缩过程的数值模拟 [J]. 爆炸与冲击, 2009, 29(3): 289–294. DOI: 10.3321/j.issn:1001-1455.2009.03.011. ZHAO Z, LI X J, TAO G, et al. Numerical simulation of the process of pore collapse under shock load [J]. Explosion and Shock Waves, 2009, 29(3): 289–294. DOI: 10.3321/j.issn:1001-1455.2009.03.011.
[13]	ESPINOSA H D, ZSVATTIERI P D. A grain level model for the study of failure initiation and evolution in polycrystalline brittle materials: part II: numerical examples [J]. Mechanics of Materials, 2003, 35(3-6): 365–394. DOI: 10.1016/S0167-6636(02)00287-9.
[14]	BRANICIO P S, KALIA R K, NAKANO A, et al. Atomistic damage mechanisms during hypervelocity projectile impact on AIN: a large-scale parallel molecular dynamics simulation study [J]. Journal of the Mechanics and Physics of Solids, 2008, 56(5): 1955–1988. DOI: 10.1016/j.jmps.2007.11.004.
[15]	YU Y, WANG W Q, HE H L, et al. Modeling multiscale evolution of numerous voids in shocked brittle material [J]. Physical Review E, 2014, 89(4): 043309. DOI: 10.1103/PhysRevE.89.043309.
[16]	YU Y, WANG W Q, HE H L, et al. Mesoscopic deformation features of shocked porous ceramic: polycrystalline modeling and experimental observations [J]. Journal of Applied Physics, 2015, 117: 125901. DOI: 10.1063/1.4916244.
[17]	POTYONDY D O. A flat-jointed bonded-particle material for hard rock [C]//The 46th U.S. Rock Mechanics/Geomechanics Symposium. Chicago, USA: ARMA, 2012. https://www.onepetro.org/conference-paper/ARMA-2012-501.
[18]	JIANG Z X, WANG Y G, NIE H C, et al. Influence of porosity on nonlinear mechanical properties of unpoled porous Pb(Zr_0.95Ti_0.05)O₃ ceramics under uniaxial compression [J]. Mechanics of Materials, 2016, 104: 139–144. DOI: 10.1016/j.mechmat.2016.11.001.
[19]	WENG J D, WANG X, MA Y, et al. A compact all-fiber displacement interferometer for measuring the foil velocity driven by laser [J]. Review of Scientific Instruments, 2008, 79(11): 111101. DOI: 10.1063/1.3020700.
[20]	CUNDALL P A, STRACK O D L. A discrete numerical model for granular assembles [J]. Geotechnique, 1979, 29(1): 47–65. DOI: 10.1680/geot.1979.29.1.47.
[21]	POTYONDY D O, CUNDALL P A. A bonded-particle model for rock [J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41: 1329–1364. DOI: 10.1016/j.ijrmms.2004.09.011.
[22]	CHO N, MARTIN C D, SEGO D C. A clumped particle model for rock [J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(7): 1329–1364. DOI: 10.1016/j.ijrmms.2007.02.002.
[23]	CHEN M W, MCCAULEY J W, DANDEKAR D P, et al. Dynamic plasticity and failure of high-purity alumina under shock loading [J]. Nature Materials, 2006, 5(8): 614–618. DOI: 10.1038/nmat1689.
[24]	熊迅, 李天密, 周风华, 等. 石英玻璃圆环高速膨胀碎裂过程的离散元模拟 [J]. 力学学报, 2018, 50(3): 622–632. DOI: 10.6052/0459-1879-17-410. XIONG X, LI T M, ZHOU F H, et al. Discrete element simulations of the high velocity expansion and fragmentation of quartz glass rings [J]. Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(3): 622–632. DOI: 10.6052/0459-1879-17-410.