近距离爆炸比例爆距的界定标准及荷载模型

甘露; 陈力; 宗周红; 钱海敏

doi:10.11883/bzycj-2020-0194

近距离爆炸比例爆距的界定标准及荷载模型

doi: 10.11883/bzycj-2020-0194

东南大学爆炸安全防护教育部工程研究中心，江苏南京 211189

基金项目: 国家自然科学基金面上项目（51678141，51978166）

详细信息

作者简介:
甘　露（1996－　），男，博士研究生，ganlu_1996@seu.edu.cn

通讯作者:
宗周红（1966－　），男，博士，教授，zongzh@seu.edu.cn

中图分类号: O383.1
计量
- 文章访问数: 1010
- HTML全文浏览量: 496
- PDF下载量: 202
- 被引次数: 0
出版历程
- 收稿日期: 2020-06-12
- 修回日期: 2020-10-13
- 网络出版日期: 2021-06-01
- 刊出日期: 2021-06-05

Definition of scaled distance of close-in explosion and blast load calculation model

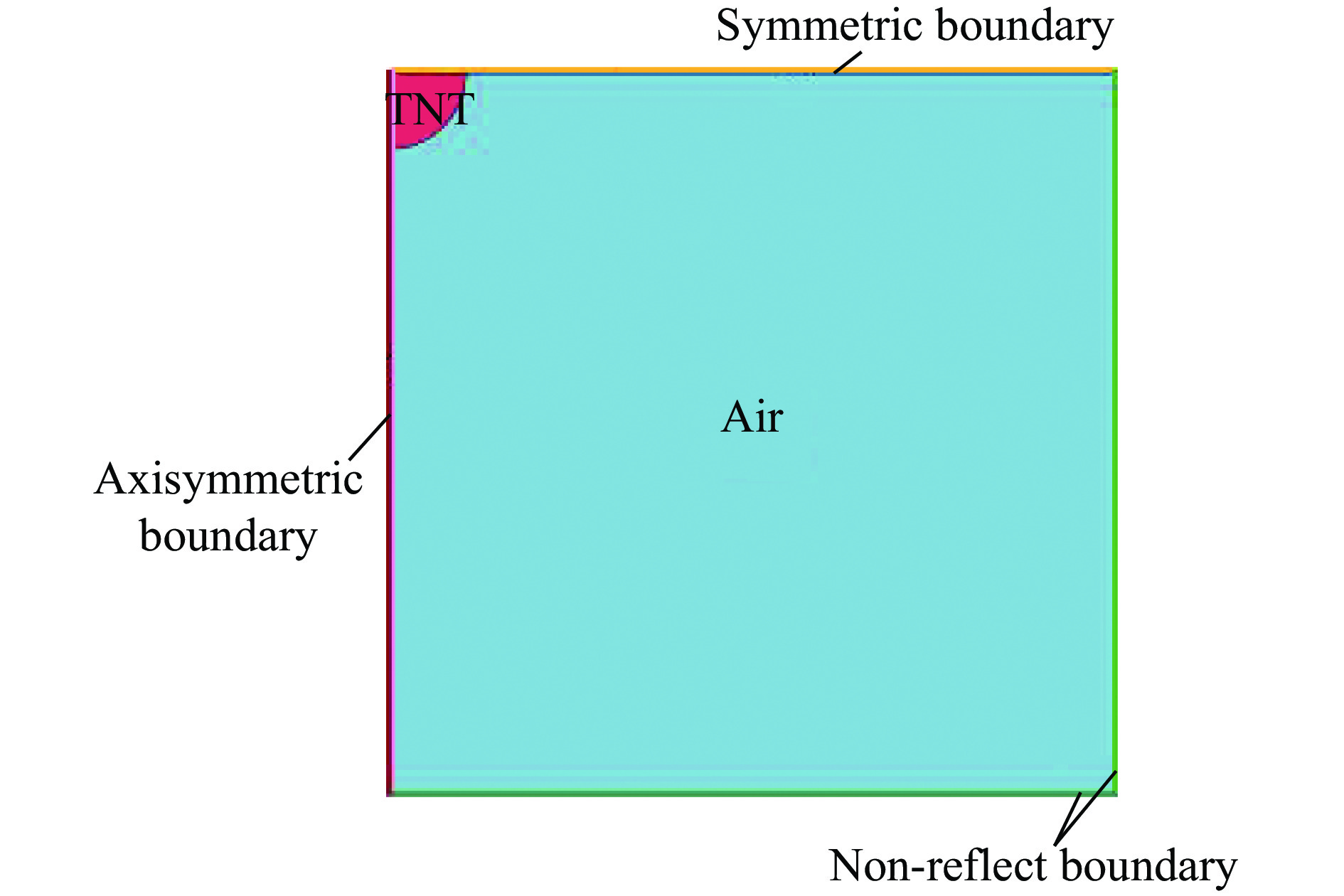
Engineering Research Center of Safety and Protection of Explosion & Impact of Ministry of Education, Southeast University, Nanjing 211189, Jiangsu, China

摘要

摘要: 如何准确界定“近距离爆炸（close-in explosion）”一直是防护工程研究领域的热点。本文中基于已被充分验证的精细化有限元模型，研究了TNT球形装药自由场爆炸冲击波传播与爆轰产物高速膨胀共同作用的特点和规律，发现在比例爆距小于0.80 m/kg^1/3的范围内，爆轰产物对刚性壁面的爆炸荷载影响显著，提出球形装药近距离爆炸的比例爆距界定标准为0.30～0.80 m/kg^1/3。研究发现，在近距离爆炸下，爆炸波在入射角为0°～5°范围内的刚性壁面反射荷载峰值会出现急剧下降的现象，这是由爆轰产物喷射的不均匀性和随机性导致的；近距离爆炸下，刚性壁面反射超压出现了两个峰值的现象，这是由冲击波和爆轰产物分别与刚性壁面相互作用导致的。提出了近距离爆炸情况下两个荷载峰值的计算公式，以及适合工程结构响应计算的简化荷载模型；揭示了近距离爆炸下刚性壁面反射超压的分布规律。
- 爆轰产物 /
- 比例爆距 /
- 近距离爆炸 /
- 荷载模型
Abstract: How to accurately define “close-in explosion” has always been a hotspot in the field of protection engineering research. In this paper, based on the fully validated 2D axisymmetric fine finite element model, the characteristics and laws of the propagation of air shock waves and high-speed expansion of detonation products generated by TNT spherical charge were studied. It is found that there is a significant influence of the detonation products on the blast load on rigid wall when the range of the scaled distance less than 0.8 m/kg^1/3. It is recommended to use the scaled distance range from 0.30 m/kg^1/3 to 0.80 m/kg^1/3 as the definition criterion of close-in explosion for spherical TNT charge explosion. It was found that: due to the inhomogeneity and randomness of the detonation product rapid expansion, the peak value of the rigid-wall reflected overpressure experienced a sharp drop within a range of incident angle of 0°～5° in the case of close-in explosion defined in the paper. In addition, there were two peaks on the reflected overpressure curve in close-in explosion cases, and the first peak overpressure was caused by the interaction between the shock wave and rigid wall while the second peak overpressure was generated by the interaction between the detonation products and rigid wall. Based on curve fitting, the formulas for calculating the two peak values were proposed, respectively, and a simplified load model suitable for calculation of engineering structure response was put forward; The distribution law of the reflected overpressure on the rigid wall under close-in explosion was revealed.
- detonation products /
- scaled distance /
- close-in explosion /
- load calculation model

HTML全文

图 1 2D轴对称模型

Figure 1. 2D axisymmetric model

下载: 全尺寸图片幻灯片

图 2 有限元网格划分

Figure 2. Mesh of the finite element model

下载: 全尺寸图片幻灯片

图 3 不同网格尺寸情况下超压峰值与比例爆距的关系

Figure 3. Peak overpressure versus scaled distances with different mesh sizes

下载: 全尺寸图片幻灯片

图 4 自由场超压峰值与比例爆距的关系

Figure 4. Incident free-field overpressures versus scaled distances

下载: 全尺寸图片幻灯片

图 5 正反射超压峰值与比例爆距的关系

Figure 5. Reflected overpressures versus scaled distances

下载: 全尺寸图片幻灯片

图 6 爆轰产物膨胀过程

Figure 6. Expansion of detonation products

下载: 全尺寸图片幻灯片

图 7 5种比例爆距工况的刚体反射超压曲线

Figure 7. Reflected overpressure curves at five types of scale distances

下载: 全尺寸图片幻灯片

图 8 0.50 m/kg^1/3比例爆距工况下冲击波反射与爆轰产物撞击作用现象

Figure 8. Reflection of blast wave and detonation product at 0.50 m/kg^1/3

下载: 全尺寸图片幻灯片

图 9 冲击波与爆轰产物到达时间及荷载峰值

Figure 9. Scaled arrival times and peak pressures of shock wave and detonation products

下载: 全尺寸图片幻灯片

图 10 板面荷载计算范围

Figure 10. Calculated scope of load distribution

下载: 全尺寸图片幻灯片

图 11 不同比例爆距工况下刚性壁面荷载峰值分布

Figure 11. Load distributions at different types of scale distances

下载: 全尺寸图片幻灯片

图 12 冲击波正反射超压峰值拟合曲线（0.30 m/kg^1/3＜Z≤0.80 m/kg^1/3）

Figure 12. Fitting curve of peak normal reflected overpressures of shock waves (0.3 m/kg^1/3＜Z≤0.8 m/kg^1/3)

下载: 全尺寸图片幻灯片

图 13 冲击波到达比时间拟合曲线（0.30 m/kg^1/3＜Z≤0.80 m/kg^1/3）

Figure 13. Fitting curve of scaled arrival times of shock waves (0.30 m/kg^1/3＜Z≤0.80 m/kg^1/3)

下载: 全尺寸图片幻灯片

图 14 爆轰产物荷载峰值拟合曲线（0.30 m/kg^1/3＜Z≤0.80 m/kg^1/3）

Figure 14. Fitting curve of peak overpressures of detonation products (0.30 m/kg^1/3＜Z≤0.80 m/kg^1/3)

下载: 全尺寸图片幻灯片

图 15 爆轰产物到达比时间拟合曲线（0.30 m/kg^1/3＜Z≤0.80 m/kg^1/3）

Figure 15. Fitting curve of scaled arrival times of detonation products (0.30 m/kg^1/3＜Z≤0.80 m/kg^1/3)

下载: 全尺寸图片幻灯片

图 16 比冲量结果曲线（0.30 m/kg^1/3＜Z≤0.80 m/kg^1/3）

Figure 16. Scaled impulses fitting curves for 0.30 m/kg^1/3＜Z≤0.80 m/kg^1/3

下载: 全尺寸图片幻灯片

图 17 荷载简化计算模型

Figure 17. A simplified calculation model for load

下载: 全尺寸图片幻灯片

图 18 刚性壁面荷载分布区间

Figure 18. Distribution of blast loads on rigid walls

下载: 全尺寸图片幻灯片

表 1 炸药模型参数^[17]

Table 1. Parameters for modeling TNT explosive^[17]

密度/（kg·m⁻³）爆速/（m·s⁻¹） p_CJ/GPa A/GPa B/GPa w R₁ R₂ E/（MJ·m⁻³）

1630 6930 21 371.2 3.231 0.3 4.15 0.95 7000

下载: 导出CSV

表 2 空气模型参数

Table 2. Parameters for modeling air

密度/（kg·m⁻³） C₀ C₁ C₂ C₃ C₄ C₅ C₆ E/（MJ·m⁻³）

1.2929 0 0 0 0 0.4 0.4 0 0.25

下载: 导出CSV

参考文献(21)

[1]	BRODE H L. Blast wave from a spherical charge [J]. The Physics of Fluids, 1959, 2(2): 217–229. DOI: 10.1063/1.1705911.
[2]	HENRYCH J. The dynamics of explosion and its use [M]. New York: Elsevier, 1979.
[3]	BAKER W E. Explosions in air [M]. Austin: University of Texas Press, 1973.
[4]	KINGERY C N, BULMASH G. Air blast parameters from TNT spherical air burst and hemispherical surface burst [R]. Aberdeen, Maryland, USA: US Army Ballistic Research Laboratory, 1984.
[5]	US Department of Defense. UFC 3-340-02 Structures to resist the effects of accidental explosions [S]. Washington: The US Department of Army, 2008.
[6]	SHIN J, WHITTAKER A, AREF A, et al. Air-blast effects on civil structures: MCEER-14-0006 [R]. Buffalo: Multidisciplinary Center for Earthquake Engineering Research, 2014. DOI: 10.13140/RG.2.1.3454.1686.
[7]	SHIN J, WHITTAKER A S, CORMIE D. Incident and normally reflected overpressure and impulse for detonations of spherical high explosives in free air [J]. Journal of Structural Engineering, 2015, 141(12): 04015057. DOI: 10.1061/(ASCE)ST.1943-541X.0001305.
[8]	SHIN J, WHITTAKER A S, CORMIE D, et al. Numerical modeling of close-in detonations of high explosives [J]. Engineering Structures, 2014, 81: 88–97. DOI: 10.1016/j.engstruct.2014.09.022.
[9]	KARLOS V, SOLOMOS G, LARCHER M. Analysis of blast parameters in the near-field for spherical free-air explosions: JRC101039 [R]. Italy: Joint Research Center, 2016. DOI: 10.2788/778898.
[10]	American Society of Civil Engineers. Blast protection of buildings [M]. New York: ASCE/ Structural Engineering Institute, 2011. DOI: 10.1061/9780784411889.
[11]	宁建国, 王成, 马天宝. 爆炸与冲击动力学[M]. 北京: 国防工业出版社, 2010: 110.
[12]	胡攀. 近距离爆炸下作用在建筑结构上的爆炸荷载模型研究[D]. 天津: 天津大学, 2016: 10.
[13]	ORTON S L, CHIARITO V P, MINOR J K, et al. Experimental testing of CFRP-strengthened reinforced concrete slab elements loaded by close-in blast [J]. Journal of Structural Engineering, 2014, 140(2): 04013060. DOI: 10.1061/(ASCE)ST.1943-541X.0000821.
[14]	李臻, 刘彦, 黄风雷, 等. 接触爆炸和近距离爆炸比冲量数值仿真研究 [J]. 北京理工大学学报, 2020, 40(2): 143–149. DOI: 10.15918/j.tbit1001-0645.2019.049. LI Z, LIU Y, HUANG F L, et al. Investigation of specific impulse under contact explosion and close-in explosion conditions using numerical method [J]. Transactions of Beijing Institute of Technology, 2020, 40(2): 143–149. DOI: 10.15918/j.tbit1001-0645.2019.049.
[15]	汪维, 刘光昆, 赵强, 等. 近爆作用下方形板表面爆炸载荷分布函数研究 [J]. 中国科学: 物理学力学天文学, 2020, 50(2): 024615. DOI: 10.1360/SSPMA-2019-0188. WANG W, LIU G K, ZHAO Q, et al. Study on load distributing function of square slab surface under close-in blast loading [J]. Scientia Sinica Physica, Mechanica & Astronomica, 2020, 50(2): 024615. DOI: 10.1360/SSPMA-2019-0188.
[16]	SMILOWITZ R, BLEWETT W, WILLIAMS P, et al. Design guidance for shelters and safe rooms (Providing protection to people and buildings against terrorist attacks) [R]. Washington: Federal Emergency Management Agency, 2006.
[17]	DOBRATZ B M, CRAWFORD P C. LLNL explosives handbook: properties of chemical explosives and explosive simulants: UCRL-52997 [R]. Livermore, California: Lawrence Livermore National Lab, 1981.
[18]	赵铮, 陶钢, 杜长星. 爆轰产物JWL状态方程应用研究 [J]. 高压物理学报, 2009, 23(4): 277–282. DOI: 10.3969/j.issn.1000-5773.2009.04.007. ZHAO Z, TAO G, DU C X. Application research on JWL equation of state of detonation products [J]. Chinese Journal of High Pressure Physics, 2009, 23(4): 277–282. DOI: 10.3969/j.issn.1000-5773.2009.04.007.
[19]	JIANG Z L. Shock waves [M]. Berlin: Springer, 2005: 855−860.
[20]	DROTLEFF J E, VINCENT C T, MULLIN S A, et al. Research in close-in blast loading from high explosives: ARL-CR-308 [R]. Virginia: U.S. Army Research Laboratory, 1996.
[21]	周丰峻, 陈叶青, 任辉启. 爆炸近区空气冲击波规则反射和非规则反射[C] // 祝贺郑哲敏先生八十华诞应用力学报告会——应用力学进展论文集. 北京: 中国力学学会, 2004: 98−112.