改进的Whipple防护结构与相关数值模拟方法研究进展

陈莹; 陈小伟

doi:10.11883/bzycj-2020-0289

改进的Whipple防护结构与相关数值模拟方法研究进展

doi: 10.11883/bzycj-2020-0289

陈莹^1,,
陈小伟^{2, 3, ,}

1.
北京理工大学机电学院，北京 100081
2.
北京理工大学爆炸科学与技术国家重点实验室，北京 100081
3.
北京理工大学前沿交叉科学研究院，北京 100081

基金项目: 国家自然科学基金（11627901，11872118）

详细信息

作者简介:
陈　莹（1996－　），女，博士研究生，604544512@qq.com

通讯作者:
陈小伟（1967－　），男，博士，教授，chenxiaoweintu@bit.edu.cn

中图分类号: O385
计量
- 文章访问数: 941
- HTML全文浏览量: 492
- PDF下载量: 201
- 被引次数: 0
出版历程
- 收稿日期: 2020-08-24
- 修回日期: 2020-09-03
- 网络出版日期: 2021-02-02
- 刊出日期: 2021-02-05

A review on the improved Whipple shield and related numerical simulations

CHEN Ying^1
,,
CHEN Xiaowei^{2, 3
, ,}

1.
School of Mechatronical Engineering, Beijing Institute of Technology, Beijing 100081, China
2.
State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China
3.
Advanced Research Institute of Multidisciplinary Science, Beijing Institute of Technology, Beijing 100081, China

摘要

摘要: 基于弹丸在超高速撞击薄板时破碎形成碎片云的机理，Whipple防护结构能够对航天器所面临的空间碎片及微流星体等威胁形成有效防护。通过回顾Whipple防护结构的研究和发展历程，对多层板结构、填充式防护结构、夹芯板结构等进行对比，分析其力学效应和防护性能；总结可应用于含泡沫、蜂窝、梯度和编织等材料的防护结构超高速撞击的数值模拟方法及其改进方法；结合相关材料的超高速撞击试验及数值模拟结果，为防护结构未来的研究方向提出建议。
- 超高速碰撞 /
- Whipple防护结构 /
- 碎片云 /
- 多层板结构 /
- 填充/夹芯板结构 /
- FEM-SPH自适应耦合算法
Abstract: Based on the formation mechanism of the debris cloud caused by the projectile hypervelocity impacting onto a thin plate, the Whipple shield can effectively protect the spacecraft from space debris and micrometeoroid. By reviewing the research and development of the Whipple shield, and compares the mechanical effects and protective performance of multilayer, stuffed and sandwich shield. The paper also summarizes the application of numerical simulation methods and their improvement for the hypervelocity impact of protective structures containing materials such as foam and honeycomb, etc. By addressing the results of hypervelocity impact tests and numerical simulations of relevant materials, suggestions are made for the future research of the Whipple shield.
- hypervelocity impact /
- Whipple shield /
- debris cloud /
- multilayer shield /
- stuffed/sandwich shield /
- FEM-SPH adaptive method

HTML全文

图 1 Whipple防护结构^[5]

Figure 1. Whipple shield^[5]

下载: 全尺寸图片幻灯片

图 2 碎片云结构（球形弹丸）^[6]

Figure 2. Debris cloud structure (spherical projectile)^[6]

下载: 全尺寸图片幻灯片

图 3 Multi-shock (MS)防护结构^[10]

Figure 3. Multi-shock shield^[10]

下载: 全尺寸图片幻灯片

图 4 Mesh double-bumper（MDB）防护结构^[10]

Figure 4. Mesh double-bumper shield^[10]

下载: 全尺寸图片幻灯片

图 5 填充式防护结构^[14]

Figure 5. Stuffed Whipple shield^[14]

下载: 全尺寸图片幻灯片

图 6 填充式泡沫铝防护结构^[30]

Figure 6. Al-form stuffed Whipple shield^[30]

下载: 全尺寸图片幻灯片

图 7 填充式泡沫铝防护结构与传统Whipple防护结构的弹道极限曲线^[33]

Figure 7. Ballistic limit curves of Al-form stuffed Whipple shield and Whipple shield^[33]

下载: 全尺寸图片幻灯片

图 8 弹丸高速撞击蜂窝铝夹芯板的破碎过程^[41]

Figure 8. Simulation of hypervelocity impacts on honeycomb sandwich structure^[41]

下载: 全尺寸图片幻灯片

图 9 不同入射角度蜂窝铝夹芯板防护结构的弹道极限曲线^[39]

Figure 9. Projectile critical perforation diameter as a function of impact velocity against the same honeycomb panel^[39]

下载: 全尺寸图片幻灯片

图 10 泡沫铝夹芯板防护结构示意图^[32]

Figure 10. Schematic configuration of Al-foam sandwiched shield^[32]

下载: 全尺寸图片幻灯片

图 11 开孔泡沫夹芯板和蜂窝夹芯板损伤对比^[50]

Figure 11. Comparison of damages in open-cell foam core and honeycomb core sandwiches^[50]

下载: 全尺寸图片幻灯片

图 12 等质量的不同Whipple防护结构弹道极限曲线对比^[48]

Figure 12. Comparison of ballistic limit curves for comparable weight/standoff Whipple shield types^[48]

下载: 全尺寸图片幻灯片

图 13 开孔泡沫孔隙与泡沫孔大小和不同孔隙率的孔隙形状示意图^[48]

Figure 13. Open cell foam pore and cell size and ligament cross section variation with relative density^[48]

下载: 全尺寸图片幻灯片

图 14 双层蜂窝结构(DL-H) 和双层泡沫结构(DL-F) ^[16]

Figure 14. Schematic of the double-layer honeycomb target and the double-layer foam target ^[16]

下载: 全尺寸图片幻灯片

图 15 350 μs时SPH和FER方法碎片的比较^[95]

Figure 15. Comparison of debris cloud results between SPH and FER at 350 μs^[95]

下载: 全尺寸图片幻灯片

图 16 5种不同冲击速度下球形弹体的损伤对比^[111]

Figure 16. Damage in aluminum spheres due to impact with aluminum bumpers at five different velocities^[111]

下载: 全尺寸图片幻灯片

图 17 自适应耦合算法所得碎片云形态^[119]

Figure 17. The debris cloud of FEM-SPH adaptive method^[119]

下载: 全尺寸图片幻灯片

图 18 泡沫材料试件与Voronoi泡沫模型对比^[135]

Figure 18. Comparison of the Al-foam with the Voronoi tessellation model^[135]

下载: 全尺寸图片幻灯片

图 19 泡沫结构生成算法示意图^[138]

Figure 19. Schematic illustration of the algorithm for foam structure generation^[138]

下载: 全尺寸图片幻灯片

图 20 相邻两个孔间胞壁厚度示意图^[139]

Figure 20. Schematic diagram of the cell-wall thickness between the two adjacent pores^[139]

下载: 全尺寸图片幻灯片

图 21 闭孔金属泡沫的有限元单元^[139]

Figure 21. Finite element grid of closed-cell metallic foams^[139]

下载: 全尺寸图片幻灯片

图 22 有限元模型不同截面和CT扫描得到的灰度图像对比^[152]

Figure 22. Comparison of different section and gray images of finite element model^[152]

下载: 全尺寸图片幻灯片

参考文献(152)

[1]	ANZ-MEADOR P D, OPIELA J N, SHOOTS D, et al. History of on-orbit satellite fragmentations: NASA/TM-2018-220037 [R]. Houston, Texas: Lyndon B. Johnson Space Center, NASA, 2018.
[2]	龚自正, 徐坤博, 牟永强, 等. 空间碎片环境现状与主动移除技术 [J]. 航天器环境工程, 2014, 31(2): 129–135. DOI: 10.12126/see.2014.02.003. GONG Z Z, XU K B, MU Y Q, et al. The space debris environment and the active debris removal techniques [J]. Spacecraft Environment Engineering, 2014, 31(2): 129–135. DOI: 10.12126/see.2014.02.003.
[3]	郑世贵, 闫军. 空间碎片防护需求与防护材料进展 [J]. 国际太空, 2014(6): 49–53. ZHENG S G, YAN J. A review on the space debris protection and protective materials [J]. Space International, 2014(6): 49–53.
[4]	龚自正, 杨继运, 张文兵, 等. 航天器空间碎片超高速撞击防护的若干问题 [J]. 航天器环境工程, 2007, 24(3): 125–130. DOI: 10.3969/j.issn.1673-1379.2007.03.001. GONG Z Z, YANG J Y, ZHANG W B, et al. Spacecraft protection from the hypervelocity impact of space meteoroid and orbital debris [J]. Spacecraft Environment Engineering, 2007, 24(3): 125–130. DOI: 10.3969/j.issn.1673-1379.2007.03.001.
[5]	WHIPPLE F L. Meteorites and space travel [J]. The Astronomical Journal, 1947, 52: 131. DOI: 10.1086/106009.
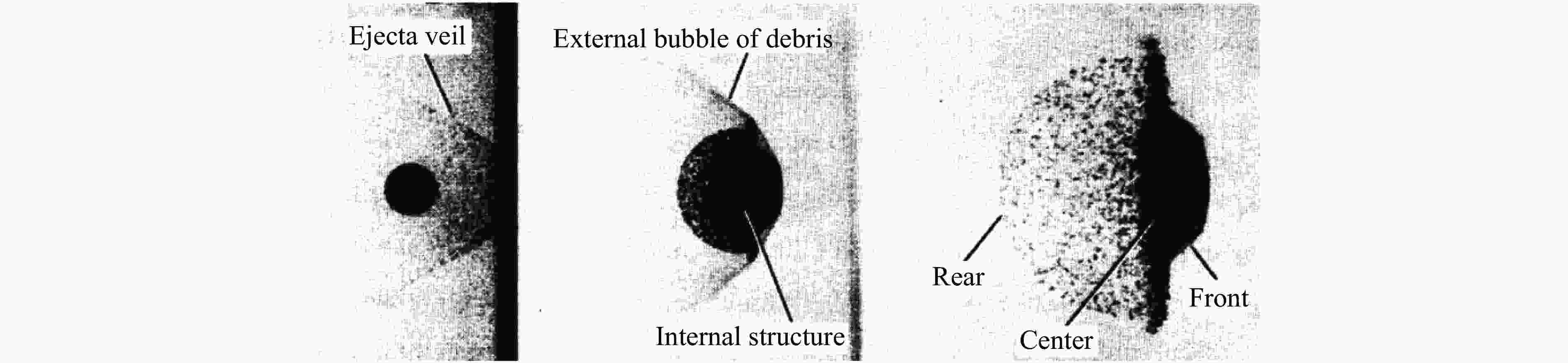
[6]	PIEKUTOWSKI A J. Formation and description of debris clouds produced by hypervelocity impact [R]. Huntsville, Alabama: Marshall Space Flight Center, NASA, 1996.
[7]	ANDERSON JR C E, TRUCANO T G, MULLIN SA. Debris cloud dynamics [J]. International Journal of Impact Engineering, 1990, 9(1): 89–113. DOI: 10.1016/0734-743X(90)90024-P.
[8]	PIEKUTOWSKI A J. Debris clouds generated by hypervelocity impact of cylindrical projectiles with thin aluminum plates [J]. International Journal of Impact Engineering, 1987, 5(1–4): 509–518. DOI: 10.1016/0734-743X(87)90066-2.
[9]	MORRISON R H. A preliminary investigation of projectile shape effects in hypervelocity impact of a double-sheet structure: TN-D-6944 [R]. Washington: National Aeronautics and Space Administration, 1972.
[10]	MACLAY T D, CULP R D, BAREISS L, et al. Topographically modified bumper concepts for spacecraft shielding [J]. International Journal of Impact Engineering, 1993, 14(1–4): 479–489. DOI: 10.1016/0734-743X(93)90044-8.
[11]	COUR-PALAIS B G, CREWS J L. A multi-shock concept for spacecraft shielding [J]. International Journal of Impact Engineering, 1990, 10(1–4): 135–146. DOI: 10.1016/0734-743X(90)90054-Y.
[12]	CHRISTIANSEN E L. Performance equations for advanced orbital debris shields [C]// Space Programs and Technologies Conference. Huntsivolle: AIAA, 1992.
[13]	CREWS J L, CHRISTIANSEN E L. The NASA JSC hypervelocity impact test facility (HIT-F) [C]// Space Programs and Technologies Conference. Huntsivolle: AIAA, 1992. DOI: 10.2514/6.1992-1640.
[14]	CHRISTIANSEN E L, CREWS J L, WILLIAMSEN J E, et al. Enhanced meteoroid and orbital debris shielding [J]. International Journal of Impact Engineering, 1995, 17(1–3): 217–228. DOI: 10.1016/0734-743X(95)99848-L.
[15]	DESTEFANIS R, SCHÄFER F, LAMBERT M, et al. Enhanced space debris shields for manned spacecraft [J]. International Journal of Impact Engineering, 2003, 29(1–10): 215–226. DOI: 10.1016/j.ijimpeng.2003.09.019.
[16]	RYAN S, HEDMAN T, CHRISTIANSEN E L. Honeycomb vs. foam: evaluating potential upgrades to ISS module shielding [J]. Acta Astronautica, 2010, 67: 818–825. DOI: 10.1016/j.actaastro.2010.05.021.
[17]	周昊, 郭锐, 南博华, 等. 填充式波纹夹层结构超高速撞击特性仿真 [J]. 国防科技大学学报, 2017, 39(2): 57–63. DOI: 10.11887/j.cn.201702008. ZHOU H, GUO R, NAN B H, et al. Simulation on hypervelocity impact characteristics of stuffed corrugation-cored sandwiches [J]. Journal of National University of Defense Technology, 2017, 39(2): 57–63. DOI: 10.11887/j.cn.201702008.
[18]	SCHONBERG W P, TULLOS R J. Spacecraft wall design for increased protection against penetration by orbital debris impacts [J]. AIAA Journal, 1991, 29(12): 2207–2214. DOI: 10.2514/6.1990-3663.
[19]	KAWAI N, KURODA Y, NAGANO M, et al. Stress-wave propagation and damage formation associated with hypervelocity penetration into polycarbonate [J]. Procedia Engineering, 2017, 204: 255–261. DOI: 10.1016/j.proeng.2017.09.733.
[20]	KUMAR S K S, JURADO-MANRIQUEZ E A, KIM Y H, et al. Polybenzimidazole (PBI) film coating for improved hypervelocity impact energy absorption for space applications [J]. Composite Structures, 2018, 188: 72–77. DOI: 10.1016/j.compstruct.2017.12.052.
[21]	LI T, YU X, LIU H F, et al. Tensile behavior of C/SiC composites plate after hypervelocity penetration: residual strength and fracture mechanism [J]. Composite Structures, 2018, 189: 378–385. DOI: 10.1016/j.compstruct.2018.01.058.
[22]	WU Q, ZHANG Q M, LONG R R, et al. Potential space debris shield structure using impact-initiated energetic materials composed of polytetrafluoroethylene and aluminum [J]. Applied Physics Letters, 2016, 108: 135–183. DOI: 10.1063/1.4943584.
[23]	COUR-PALAIS B G. Meteorid environment model: NASA/SP-8013 [R]. Washington: National Aeronautics and Space Administration, 1969. DOI: CDSTIC.GRA.00159492.
[24]	CHRISTIANSEN E L. Meteoroid/debris shielding: NASA/TP-2003-210788 [R]. Houston, Texas: NASA Johnson Space Center, 2003.
[25]	HAYASHIDA K B, ROBINSON J H. Double-plate penetration equations: NASA/TM-2000-209907 [R]. Alabama: Marshall Space Flight Center, NASA, 2000.
[26]	郑建东, 龚自正, 童靖宇, 等. 一种新的Whipple防护结构弹道极限方程准确率分析 [J]. 航天器环境工程, 2012, 29(2): 134–138. DOI: 10.3969/j.issn.1673-1379.2012.02.004. ZHENG J D, GONG Z Z, TONG J Y, et al. Accuracy analysis of a new Whipple shield ballistic limit equations [J]. Spacecraft Environment Engineering, 2012, 29(2): 134–138. DOI: 10.3969/j.issn.1673-1379.2012.02.004.
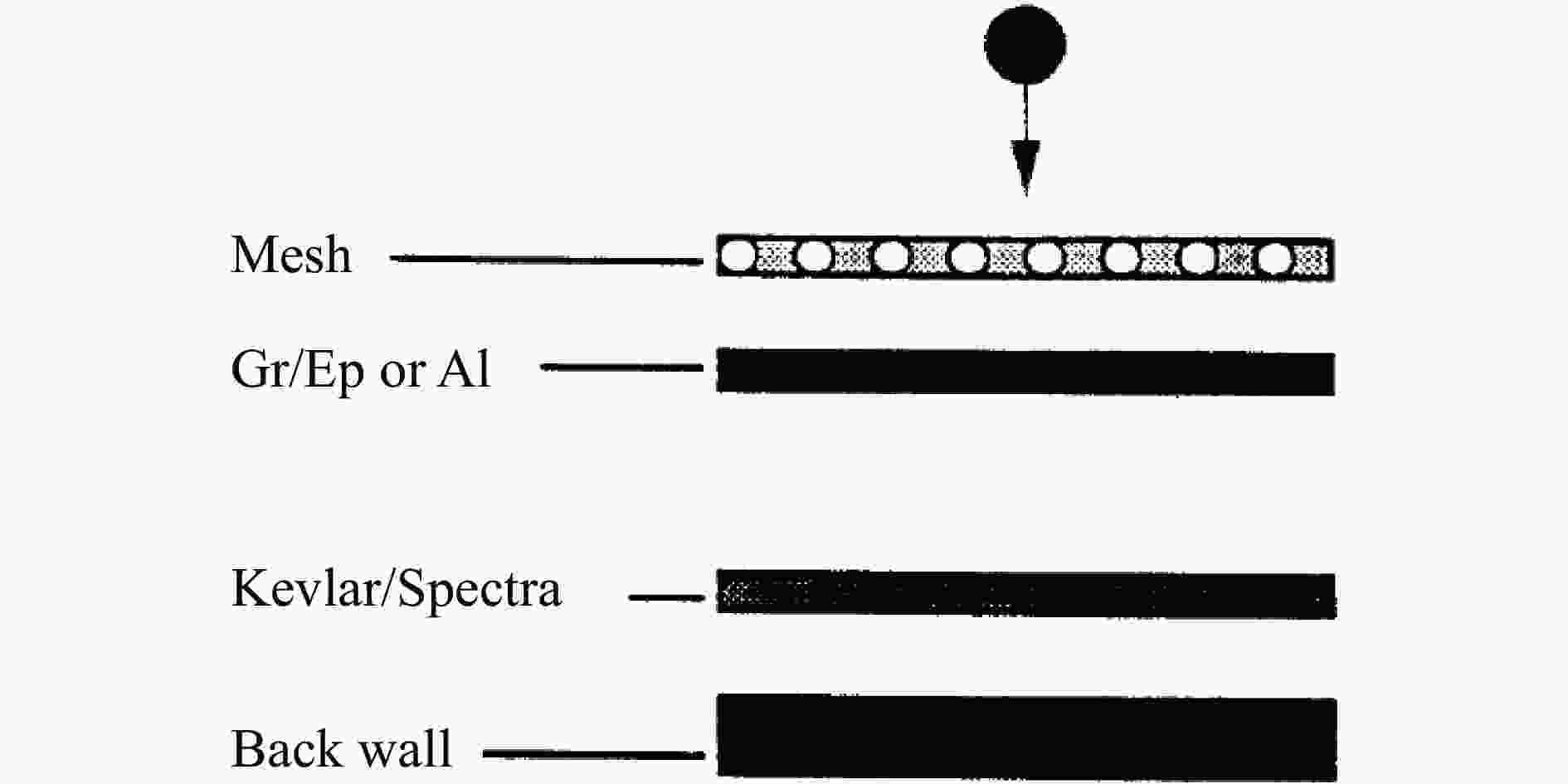
[27]	CHRISTIANSEN E L, KERR J H. Mesh double-bumper shield: a low-weight alternative for spacecraft meteoroid and orbital debris protection [J]. International Journal of Impact Engineering, 1993, 14(1 –4): 169–180. DOI: 10.1016/0734-743X(93)90018-3.
[28]	CHRISTIANSEN E L. Advanced meteoroid and debris shielding concepts [C]// Orbital Debris Conference: Technical Issues and Future Directions, AIAA. 1990. DOI: 10.2514/6.1990-1336.
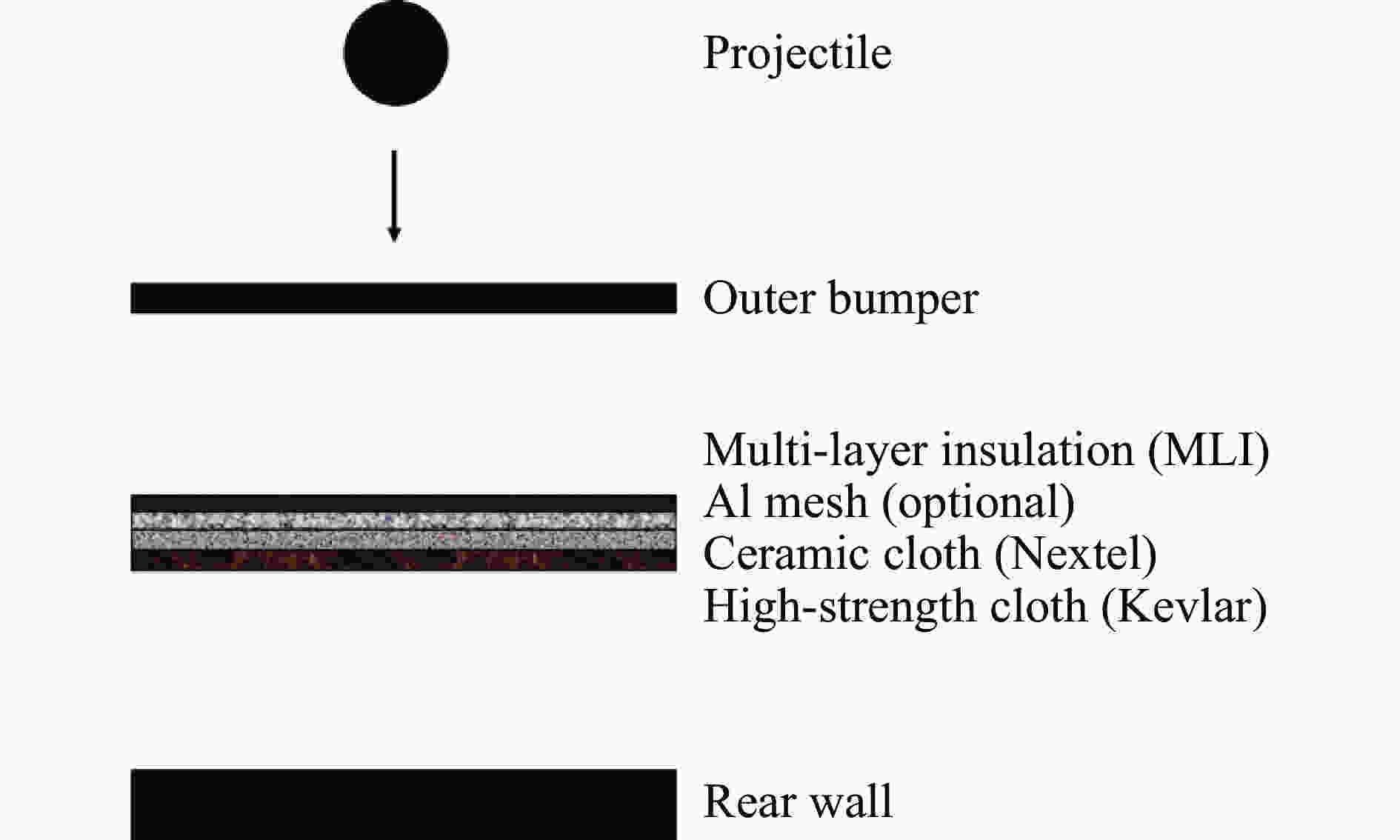
[29]	CHRISTIANSEN E L, KERR J H, DE LA FUENTE H M, et al. Flexible and deployable meteoroid/debris shielding for spacecraft [J]. International Journal of Impact Engineering, 1999, 23: 125–136. DOI: 10.1016/S0734-743X(99)00068-8.
[30]	RYAN S, CHRISTIANSEN E L. Hypervelocity impact testing of advanced materials and structures for micrometeoroid and orbital debris shielding [J]. Acta Astronautica, 2013, 83: 216–231. DOI: 10.1016/j.actaastro.2012.09.012.
[31]	贾斌, 马志涛, 庞宝君. 填充泡沫铝防护结构的超高速撞击数值模拟 [J]. 哈尔滨工业大学学报, 2011, 43(1): 16–20. DOI: 10.11918/j.issn.0367-6234.2011.01.004. JIA B, MA Z T, PANG B J. Numerical simulation investigation in hypervelocity impact on Al-foam stuffed shields [J]. Journal of Harbin Institute of Technology, 2011, 43(1): 16–20. DOI: 10.11918/j.issn.0367-6234.2011.01.004.
[32]	贾斌, 马志涛, 庞宝君. 含泡沫铝防护结构的超高速撞击数值模拟研究 [J]. 高压物理学报, 2009, 23(6): 453–459. DOI: 10.11858/gywlxb.2009.06.009. JIA B, MA Z T, PANG B J. Numerical simulation investigation in hypervelocity impact on shield structure containing aluminum foam [J]. Chinese Journal of High Pressure Physics, 2009, 23(6): 453–459. DOI: 10.11858/gywlxb.2009.06.009.
[33]	刘文祥, 张德志, 张向荣, 等. 填充式泡沫铝防护结构的弹道极限 [J]. 爆炸与冲击, 2012, 32(1): 43–46. DOI: 10.11883/1001-1455(2012)01-0043-04. LIU W X, ZHANG D Z, ZHANG X R, et al. Ballistic limit of an aluminum foam-filledshield [J]. Explosion and Shock Waves, 2012, 32(1): 43–46. DOI: 10.11883/1001-1455(2012)01-0043-04.
[34]	DESTEFANIS R, SCHÄFER F, LAMBERT M, et al. Selecting enhanced space debris shields for manned spacecraft [J]. International Journal of Impact Engineering, 2006, 33(1–12): 219–230. DOI: 10.1016/j.ijimpeng.2006.09.065.
[35]	TAYLOR E A, GLANVILLE J P, CLEGG R A, et al. Hypervelocity impact on spacecraft honeycomb: hydrocode simulation and damage laws [J]. International Journal of Impact Engineering, 2003, 29: 691–702. DOI: 10.1016/j.ijimpeng.2003.10.016.
[36]	TAYLOR E A. Computational study of hypervelocity impact onto Whipple bumpers and sandwich plates with honeycomb core [R]. European Space Agency/European Space Research and Technology Centre, 1999.
[37]	RYAN S, SCHÄFER F, DESTEFANIS R, et al. A ballistic limit equation for hypervelocity impacts on composite honeycomb sandwich panel satellite structures [J]. Advances in Space Research, 2008, 41(7): 1152–1166. DOI: 10.1016/j.asr.2007.02.032.
[38]	SIBEAUD J-M, PRIEUR C, PUILLET C. Hypervelocity impact on honeycomb target structures: experimental part [C]// The 4th European Conference on Space Debris. Darmstadt, Germany: The European Space Agency, 2005.
[39]	SIBEAUD J-M, THAMIE L, PUILLET C. Hypervelocity impact on honeycomb target structures: experiments and modeling [J]. International Journal of Impact Engineering, 2008, 35(12): 1799–1807. DOI: 10.1016/j.ijimpeng.2008.07.037.
[40]	JEX D W, MAC KAY C, MILLER A. The characteristics of penetration for a double-sheet structure with honeycomb: NASA/TM-X-53974 [R]. Huntsville: Marshall Space Flight Center, NASA, 1970.
[41]	DECONINCK P, ABDULHAMID H, HÉREIL P L, et al. Experimental and numerical study of submillimeter-sized hypervelocity impacts on honeycomb sandwich structures [J]. Procedia engineering, 2017, 204: 452–459. DOI: 10.1016/j.proeng.2017.09.740.
[42]	NITTA K, HIGASHIDE M, KITAZAWA Y, et al. Response of a aluminum honeycomb subjected to hypervelocity impacts [J]. Procedia Engineering, 2013, 58: 709–714. DOI: 10.1016/j.proeng.2013.05.082.
[43]	SCHONBERG W, SCHÄFER F, PUTZAR R. Hypervelocity impact response of honeycomb sandwich panels [J]. Acta Astronautica, 2010, 66(3–4): 455–466. DOI: 10.1016/j.actaastro.2009.06.018.
[44]	ANON. Effectiveness of aluminum honeycomb shields in preventing meteoroid damage to liquid-filled spacecraft tanks: NASA/CR-65261 [R]. Salt Lake City: Utah Research and Development Co. Inc., NASA, 1964.
[45]	LATHROP B L, SENNETT R E. Effects of hypervelocity impact on honeycomb structures [J]. Journal of Spacecraft and Rockets, 1968, 5(12): 1496–1497. DOI: 10.2514/3.29514.
[46]	LAMBERT M, SCHÄFER F K, GEYER T. Impact damage on sandwich panels and multi-layer insulation [J]. International Journal of Impact Engineering, 2001, 26(1–10): 369–380. DOI: 10.1016/S0734-743X(01)00108-7.
[47]	KANG P, YOUN S K, LIM J H. Modification of the critical projectile diameter of honeycomb sandwich panel considering the channeling effect in hypervelocity impact [J]. Aerospace Science and Technology, 2013, 29: 413–425. DOI: 10.1016/j.ast.2013.04.011.
[48]	RYAN S, ORDONEZ E, CHRISTIANSEN E L, et al. Hypervelocity impact performance of open cell foam core sandwich panel structures [C]// The 11th Hypervelocity Impact Symposium. Freiburg, Germany, 2010.
[49]	YASENSKY J, CHRISTIANSEN E L. Hypervelocity impact evaluation of metal foam core sandwich structures: NASA/JSC63945 [R]. NASA, 2007.
[50]	RYAN S, HEDMAN T, CHRISTIANSEN E L. Honeycomb vs. foam: evaluating a potential upgrade to international space station module shielding for micrometeoroids and orbital debris: NASA/TM-2009-214793 [R]. Arizona: USRA Lunar and Planetary Institute, NASA, 2009.
[51]	VOILLAT R, GALLIEN F, MORTENSEN A, et al. Hypervelocity impact testing on stochastic and structured open porosity cast Al-Si cellular structures for space applications [J]. International Journal of Impact Engineering, 2018, 120: 126–137. DOI: 10.1016/j.ijimpeng.2018.05.002.
[52]	GAITANAROS S, KYRIAKIDES S. On the effect of relative density on the crushing and energy absorption of open-cell foams under impact [J]. International Journal of Impact Engineering, 2015, 82: 3–13. DOI: 10.1016/j.ijimpeng.2015.03.011.
[53]	SHI X P, LIU S Y, NIE H L, et al. Study of cell irregularity effects on the compression of closed-cell foams [J]. International Journal of Mechanical Sciences, 2018, 135: 215–225. DOI: 10.1016/j.ijmecsci.2017.11.026.
[54]	SANCHEZ G A, CHRISTIANSEN E L. FGB energy block meteoroid and orbital (M/OD) debris shield test report: NASA/JSC-27460 [R]. Washington: National Aeronautics and Space Administration, 1996.
[55]	THOMA K, SCHÄFER F, HIERMAIER S, et al. An approach to achieve progress in spacecraft shielding [J]. Advances in Space research, 2004, 34(5): 1063–1075. DOI: 10.1016/j.asr.2003.03.034.
[56]	张雄, 刘岩, 马上. 无网格法的理论及应用 [J]. 力学进展, 2009, 39(1): 1–36. DOI: 10.3321/j.issn:1000-0992.2009.01.001. ZHANG X, LIU Y, MA S. Meshfree methods and their applications [J]. Advances in Mechanics, 2009, 39(1): 1–36. DOI: 10.3321/j.issn:1000-0992.2009.01.001.
[57]	张雄, 宋康祖, 陆明万. 无网格法研究进展及其应用 [J]. 计算力学学报, 2003, 20(6): 730–742. DOI: 10.7511/jslx20036138. ZHANG X, SONG K Z, LU M W. Research progress and application of meshless method [J]. Chinese Journal of Computational Mechanics, 2003, 20(6): 730–742. DOI: 10.7511/jslx20036138.
[58]	胡德安, 韩旭, 肖毅华, 等. 光滑粒子法及其与有限元耦合算法的研究进展 [J]. 力学学报, 2013, 45(5): 639–652. DOI: 10.6052/0459-1879-13-092. HU D A, HAN X, XIAO Y H, et al. Research developments of smoothed particle hydrodynamicsmethod and its coupling with finite element method [J]. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(5): 639–652. DOI: 10.6052/0459-1879-13-092.
[59]	GINGOLD R A, MONAGHAN J J. Smoothed particle hydrodynamics: theory and application to non-spherical stars [J]. Monthly Notices of the Royal Astronomical Society, 1977, 181(3): 375–389. DOI: 10.1093/mnras/181.3.375.
[60]	LUCY L B. A numerical approach to the testing of the fission hypothesis [J]. The Astronomical Journal, 1977, 82(12): 1013–1024. DOI: 10.1086/112164.
[61]	LIBERSKY L D, PETSCHEK A G. Smooth particle hydrodynamics with strength of materials [J]. Advances in the Free Lagrange Method, 1990, 248: 248–257. DOI: 10.1007/3-540-54960-9_58.
[62]	LIBERSKY L D, RANDLES P W, CARNEY T C, et al. Recent improvements in SPH modeling of hypervelocity impact [J]. International Journal of Impact Engineering, 1997, 20(6–10): 525–532. DOI: 10.1016/S0734-743X(97)87441-6.
[63]	LIBERSKY L D, PETSCHEK A G, CARNEY T C, et al. High strain Lagrangian hydrodynamics: a three-dimensional SPH code for dynamic material response [J]. Journal of Computational Physics, 1993, 109(1): 67–75. DOI: 10.1006/jcph.1993.1199.
[64]	RANDLES P W, LIBERSKY L D. Smoothed particle hydrodynamics: some recent improvements and applications [J]. Computer Methods in Applied Mechanics and Engineering, 1996, 139(1–4): 375–408. DOI: 10.1016/S0045-7825(96)01090-0.
[65]	HAYHURST C J, CLEGG R A. Cylindrically symmetric SPH simulations of hypervelocity impacts on thin plates [J]. International Journal of Impact Engineering, 1997, 20(1–5): 337–348. DOI: 10.1016/S0734-743X(97)87505-7.
[66]	崔伟峰, 曾新吾. SPH算法在超高速碰撞数值模拟中的应用 [J]. 国防科技大学学报, 2007, 29(2): 43–46. DOI: 10.3969/j.issn.1001-2486.2007.02.010. CUI W F, ZENG X W. Smoothed particle hydrodynamics algorithm applied in numerical simulation of hypervelocity impact [J]. Journal of National University of Defense Technology, 2007, 29(2): 43–46. DOI: 10.3969/j.issn.1001-2486.2007.02.010.
[67]	徐志宏, 汤文辉, 罗永. SPH 算法在高速侵彻问题中的应用 [J]. 国防科技大学学报, 2005, 27(4): 41–44. DOI: 10.3969/j.issn.1001-2486.2005.04.010. XU Z H, TANG W H, LUO Y. Smoothed particle hydrodynamics algorithm applied in penetration problem [J]. Journal of National University of Defense Technology, 2005, 27(4): 41–44. DOI: 10.3969/j.issn.1001-2486.2005.04.010.
[68]	LIU G R, LIU M B, LI S F. Smoothed particle hydrodynamics: a meshfree method [J]. Computational Mechanics, 2004, 33: 491–491. DOI: 10.1007/s00466-004-0573-1.
[69]	DYKA C T, INGEL R P, FLIPPEN L D. A new approach to dynamic condensation for FEM [J]. Computers & Structures, 1995, 61(4): 763–773. DOI: 10.1016/0045-7949(96)00017-X.
[70]	SWEGLE J W, HICKS D L, ATTAWAY S W. Smoothed particle hydrodynamics stability analysis [J]. Journal of Computational Physics, 1995, 116(1): 123–134. DOI: 10.1006/jcph.1995.1010.
[71]	傅学金, 强洪夫, 杨月诚. 固体介质中SPH方法的拉伸不稳定性问题研究进展 [J]. 力学进展, 2007, 37(3): 375–388. DOI: 10.3321/j.issn:1000-0992.2007.03.005. FU X J, QIANG H F, YANG Y C. Advances in the tensile instability of smoothed particle hydrodynamics applied to solid dynamics [J]. Advances in Mechanics, 2007, 37(3): 375–388. DOI: 10.3321/j.issn:1000-0992.2007.03.005.
[72]	MORRIS J P. A study of the stability properties of smooth particle hydrodynamics [J]. Publications of the Astronomical Society of Australia, 1996, 13(1): 97–102. DOI: 10.1017/S1323358000020610.
[73]	刘谋斌, 常建忠. 光滑粒子动力学方法中粒子分布与数值稳定性分析 [J]. 物理学报, 2010, 59(6): 3654–3662. DOI: 10.7498/aps.59.3654. LIU M B, CHANG J Z. Particle distribution and numerical stability in smoothed particle hydrodynamics method [J]. Acta Physica Sinica, 2010, 59(6): 3654–3662. DOI: 10.7498/aps.59.3654.
[74]	卞梁, 王肖钧, 章杰, 等. 高速碰撞数值计算中的 SPH 分区算法 [J]. 计算物理, 2011, 28(2): 207–212. DOI: 10.3969/j.issn.1001-246X.2011.02.007. BIAN L, WANG X J, ZHANG J, et al. Numerical simulation of hypervelocity impact with subdomains in SPH computation [J]. Chinese Journal of Computational Physics, 2011, 28(2): 207–212. DOI: 10.3969/j.issn.1001-246X.2011.02.007.
[75]	倪国喜, 王瑞利, 林忠, 等. 任意区域上的粒子均匀分布方法 [J]. 计算力学学报, 2007, 24(4): 408–413. DOI: 10.3969/j.issn.1007-4708.2007.04.005. NI G X, WANG R L, LIN Z, et al. Equi-distribution of particles in arbitrary domain [J]. Chinese Journal of Computational Mechanics, 2007, 24(4): 408–413. DOI: 10.3969/j.issn.1007-4708.2007.04.005.
[76]	董晃晃. SPH 的粒子生成方法及其在弹体侵彻金属靶中的应用[D]. 南昌: 华东交通大学, 2017. DONG H H. Particle generation method for SPH and the application of SPH to penetration of metal targets by projectiles [D]. Nanchang: East China Jiaotong University, 2017.
[77]	DYKA C T, RANDLES P W, INGEL R P. Stress point for tension instability in SPH [J]. International Journal for Numerical Methods in Engineering, 1997, 40(13): 2325–2341. DOI: 10.1002/(SICI)1097-0207(19970715)40:13<2325::AID-NME161>3.0.CO,2.
[78]	MONAGHAN J J. SPH without a tensile instability [J]. Journal of Computational Physics, 2000, 159(2): 290–311. DOI: 10.1006/jcph.2000.6439.
[79]	LIU M B, LIU G R, ZONG Z. An overview on smoothed particle hydrodynamics [J]. International Journal of Computational Methods, 2008, 5(1): 135–188. DOI: 10.1142/S021987620800142X.
[80]	LIU M B, XIE W P, LIU G R. Modeling incompressible flows using a finite particle method [J]. Applied Mathematical Modelling, 2005, 29(12): 1252–1270. DOI: 10.1016/j.apm.2005.05.003.
[81]	LIU M B, LIU G R. Restoring particle consistency in smoothed particle hydrodynamics [J]. Applied Numerical Mathematics, 2006, 56(1): 19–36. DOI: 10.1016/j.apnum.2005.02.012.
[82]	杨秀峰, 刘谋斌. 光滑粒子动力学 SPH 方法应力不稳定性的一种改进方案 [J]. 物理学报, 2012, 61(22): 224701. DOI: 10.7498/aps.61.224701. YANG X F, LIU M B. Improvement on stress instability in smoothed particle hydrodynamics [J]. Acta Physica Sinica, 2012, 61(22): 224701. DOI: 10.7498/aps.61.224701.
[83]	GRADY D E, WINFREE N A. Impact fragmentation of high-velocity compact projectiles on thin plates: a physical and statistical characterization of fragment debris [J]. International Journal of Impact Engineering, 2001, 26(1 –10): 249–262. DOI: 10.1016/S0734-743X(01)00085-9.
[84]	NAKAMURA A, FUJIWARA A. Velocity distribution of fragments formed in a simulated collisional disruption [J]. Icarus, 1991, 92(1): 132–146. DOI: 10.1016/0019-1035(91)90040-Z.
[85]	HOCKNEY R W, EASTWOOD J W. Computer simulation using particles [M]. New York: McGraw-Hill, 1981.
[86]	HOCKNEY R W, EASTWOOD J W. Computer simulation using particles [M]. Boca Raton: CRC Press, 1988.
[87]	BENZ W. Smooth particle hydrodynamics: a review [C] // The Numerical Modelling of Nonlinear Stellar Pulsations. Dordrecht: NATO ASI Series, 1990: 269–288. DOI: 10.1007/978-94-009-0519-1_16.
[88]	BENZ W, ASPHAUG E. Impact simulations with fracture: I: method and tests [J]. Icarus, 1994, 107(1): 98–116. DOI: 10.1006/icar.1994.1009.
[89]	BENZ W, ASPHAUG E. Simulations of brittle solids using smooth particle hydrodynamics [J]. Computer Physics Communications, 1995, 87(1–2): 253–265. DOI: 10.1016/0010-4655(94)00176-3.
[90]	徐金中, 汤文辉, 徐志宏. 超高速碰撞碎片云特征的SPH方法数值分析 [J]. 高压物理学报, 2008, 22(4): 377–383. DOI: 10.11858/gywlxb.2008.04.007. XU J Z, TANG W H, XU Z H. Numerical analysis of the characteristics of debris clouds produced by hypervelocity impacts using SPH method [J]. Chinese Journal of High Pressure Physics, 2008, 22(4): 377–383. DOI: 10.11858/gywlxb.2008.04.007.
[91]	LIANG S C, LI Y, CHEN H, et al. Research on the technique of identifying debris and obtaining characteristic parameters of large-scale 3D point set [J]. International Journal of Impact Engineering, 2013, 56: 27–31. DOI: 10.1016/j.ijimpeng.2012.07.004.
[92]	SAKONG J, WOO S C, KIM T W. Determination of impact fragments from particle analysis via smoothed particle hydrodynamics and k-means clustering [J]. International Journal of Impact Engineering, 2019, 134: 103387. DOI: 10.1016/j.ijimpeng.2019.103387.
[93]	ZHANG X T, JIA G H, HUANG H. Fragment identification and statistics method of hypervelocity impact SPH simulation [J]. Chinese Journal of Aeronautics, 2011, 24: 18–24. DOI: 10.1016/S1000-9361(11)60003-4.
[94]	张晓天, 贾光辉, 黄海. 基于 FE 重构方法的冲击破碎仿真 [J]. 计算力学学报, 2011, 28(5): 792–797. DOI: 10.7511/jslx201105024. ZHANG X T, JIA G H, HUANG H. Combination of FE and SPH method for impact fragmentation [J]. Chinese Journal of Computational Mechanics, 2011, 28(5): 792–797. DOI: 10.7511/jslx201105024.
[95]	ZHANG X T, JIA G H, HUANG H. Finite element reconstruction approach for on-orbit spacecraft breakup dynamics simulation and fragment analysis [J]. Advances in Space Research, 2013, 51(3): 423–433. DOI: 10.1016/j.asr.2012.09.023.
[96]	张晓天, 贾光辉, 黄海. 基于超高速碰撞仿真的卫星碰撞解体碎片分析 [J]. 航空学报, 2011, 32(7): 1224–1230. DOI: CNKI:11-1929/V.20110330.1305.004. ZHANG X T, JIA G H, HUANG H. Debris analysis of on-orbit satellite collision based on hypervelocity impact simulation [J]. Acta Aeronautica Astronautica Sinica, 2011, 32(7): 1224–1230. DOI: CNKI:11-1929/V.20110330.1305.004.
[97]	ATTAAWAY S W, HEINSTEIN M W, SWEGLE J W. Coupling of smooth particle hydrodynamics with the finite element method [J]. Nuclear Engineering and Design, 1994, 150(2–3): 199–205. DOI: 10.1016/0029-5493(94)90136-8.
[98]	VUYST TD, VIGNJEVIC R, CAMPBELL J C. Coupling between meshless and finite element methods [J]. International Journal of Impact Engineering, 2005, 31(8): 1054–1064. DOI: 10.1016/j.ijimpeng.2004.04.017.
[99]	JOHNSON G R. Linking of Lagrangian particle methods to standard finite element methods for high velocity impact computations [J]. Nuclear Engineering and Design, 1994, 150(2–3): 265–274. DOI: 10.1016/0029-5493(94)90143-0.
[100]	冷冰林, 许金余, 邵宁, 等. 刚性弹丸侵彻金属靶体的 FEM-SPH 耦合计算 [J]. 弹箭与制导学报, 2008, 28(5): 105–108. DOI: 10.3969/j.issn.1673-9728.2008.05.032. LENG B L, XU J Y, SHAO N, et al. Computation of steel penetrated by rigid projectile with coupled FEM-SPH methods [J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2008, 28(5): 105–108. DOI: 10.3969/j.issn.1673-9728.2008.05.032.
[101]	肖毅华, 胡德安, 韩旭, 等. 一种自适应轴对称FEM-SPH耦合算法及其在高速冲击模拟中的应用 [J]. 爆炸与冲击, 2012, 32(4): 51–59. DOI: 10.11883/1001-1455(2012)04-0384-09. XIAO Y H, HU D A, HAN X, et al. An adaptive axisymmetric FEM-SPH coupling algorithm and its application to high velocity impact simulation [J]. Explosion and Shock Waves, 2012, 32(4): 51–59. DOI: 10.11883/1001-1455(2012)04-0384-09.
[102]	纪冲, 龙源, 方向. 基于FEM-SPH耦合法的弹丸侵彻钢纤维混凝土数值模拟 [J]. 振动与冲击, 2010, 29(7): 69–74. DOI: 10.3969/j.issn.1000-3835.2010.07.015. JI C, LONG Y, FANG X. Numerical simulation for projectile penetrating steel fiber reinforced concrete with FEM-SPH coupling algorithm [J]. Journal of Vibration and Shock, 2010, 29(7): 69–74. DOI: 10.3969/j.issn.1000-3835.2010.07.015.
[103]	武玉玉, 何远航, 李金柱. 耦合方法在超高速碰撞数值模拟中的应用 [J]. 高压物理学报, 2005, 19(4): 385–389. DOI: 10.11858/gywlxb.2005.04.019. WU Y Y, HE Y H, LI J Z. Application of the coupling method in simulating the hypervelocity impact [J]. Chinese Journal of High Pressure Physics, 2005, 19(4): 385–389. DOI: 10.11858/gywlxb.2005.04.019.
[104]	何远航, 武玉玉, 张庆明. 碰撞倾角对碎片云分布影响的数值模拟 [J]. 北京理工大学学报, 2007, 27(10): 851–854. DOI: 10.3969/j.issn.1001-0645.2007.10.002. HE Y H, WU Y Y, ZHANG Q M. Numerical simulation for the influence of impact angle on debris clouds distribution [J]. Transactions of Beijing Institute of Technology, 2007, 27(10): 851–854. DOI: 10.3969/j.issn.1001-0645.2007.10.002.
[105]	SAKONG J, WOO S C, KIM J Y, et al. Study on material fracture and debris dispersion behavior via high velocity impact [J]. Transactions of the Korean Society of Mechanical Engineers A, 2017, 41(11): 1065–1075. DOI: 10.3795/KSME-A.2017.41.11.1065.
[106]	BECKER M, SEIDL M, MEHL M, et al. Numerical and experimental investigation of SPH, SPG, and FEM for high-velocity impact applications [C]// The 12th European LS-DYNA Conference. Koblenz: DYNAmore GmbH, 2019.
[107]	JOHNSON G R, BEISSEL S R, STRYK R A. An improved generalized particle algorithm that includes boundaries and interfaces [J]. International Journal for Numerical Methods in Engineering, 2002, 53(4): 875–904. DOI: 10.1002/nme.316.
[108]	JOHNSON G R, STRYK R A. Conversion of 3D distorted elements into meshless particles during dynamic deformation [J]. International Journal of Impact Engineering, 2003, 28(9): 947–966. DOI: 10.1016/S0734-743X(03)00012-5.
[109]	JOHNSON G R. Numerical algorithms and material models for high-velocity impact computations [J]. International Journal of Impact Engineering, 2011, 38(6): 456–472. DOI: 10.1016/j.ijimpeng.2010.10.017.
[110]	JOHNSON G R, STRYK R A, BEISSEL S R, et al. An algorithm to automatically convert distorted finite elements into meshless particles during dynamic deformation [J]. International Journal of Impact Engineering, 2002, 27(10): 997–1013. DOI: 10.1016/S0734-743X(02)00030-1.
[111]	BEISSEL S R, GERLACH C A, JOHNSON G R. Hypervelocity impact computations with finite elements and meshfree particles [J]. International Journal of Impact Engineering, 2006, 33(1–12): 80–90. DOI: 10.1016/j.ijimpeng.2006.09.047.
[112]	BEISSEL S R, GERLACH C A, JOHNSON G R. A quantitative analysis of computed hypervelocity debris clouds [J]. Cement Technology, 2008, 35(12): 1410–1418. DOI: 10.1016/j.ijimpeng.2008.07.059.
[113]	JOHNSON G R, BEISSEL S R, GERLACH C A. A 3D combined particle-element method for intense impulsive loading computations involving severe distortions [J]. International Journal of Impact Engineering, 2015, 84: 171–180. DOI: 10.1016/j.ijimpeng.2015.06.006.
[114]	JOHNSON G R, BEISSEL S R, STRYK R A. A generalized particle algorithm for high velocity impact computations [J]. Computational Mechanics, 2000, 25: 245–256. DOI: 10.1007/s004660050473.
[115]	GERLACH C A, JOHNSON G R. A contact and sliding interface algorithm for the combined particle-element method [J]. International Journal of Impact Engineering, 2018, 113: 21–28. DOI: 10.1016/j.ijimpeng.2017.11.003.
[116]	SAUER M. Adaptive kopplung des netzfreien SPH-verfahrens mit finiten elementen zur berechnung von impaktvorgängen [D]. Munich: Universität der Bundeswehr München, 2000.
[117]	王吉, 王肖钧, 卞梁. 光滑粒子法与有限元的耦合算法及其在冲击动力学中的应用 [J]. 爆炸与冲击, 2007, 27(6): 44–50. DOI: 10.11883/1001-1455(2007)06-0522-07. WANG J, WANG X J, BIAN L. Linking of smoothed particle hydronamics method to standard finite element method and its application in impact dynamics [J]. Explosion and Shock Waves, 2007, 27(6): 44–50. DOI: 10.11883/1001-1455(2007)06-0522-07.
[118]	张志春, 强洪夫, 高巍然. 一种新型SPH-FEM耦合算法及其在冲击动力学问题中的应用 [J]. 爆炸与冲击, 2011, 31(3): 243–249. DOI: 10.11883/1001-1455(2011)03-0243-07. ZHANG Z C, QIANG H F, GAO W R. A new coupled SPH-FEM algorithm and its application to impact dynamics [J]. Explosion and Shock Waves, 2011, 31(3): 243–249. DOI: 10.11883/1001-1455(2011)03-0243-07.
[119]	HE Q G, CHEN X W, CHEN J F. Finite element-smoothed particle hydrodynamics adaptive method in simulating debris cloud [J]. Acta Astronautica, 2020, 175: 99–117. DOI: 10.1016/j.actaastro.2020.05.056.
[120]	PIEKUTOWSKI A J. Characteristics of debris clouds produced by hypervelocity impact of aluminum spheres with thin aluminum plates [J]. International Journal of Impact Engineering, 1993, 14(1–4): 573–586. DOI: 10.1016/0734-743X(93)90053-A.
[121]	PIEKUTOWSKI A J. Fragmentation initiation threshold for spheres impacting at hypervelocity [J]. International Journal of Impact Engineering, 2003, 29(1–10): 563–574. DOI: 10.1016/j.ijimpeng.2003.10.005.
[122]	HE Y, BAYLY A E, HASSANPOUR A, et al. A GPU-based coupled SPH-DEM method for particle-fluid flow with free surfaces [J]. Powder Technology, 2018, 338: 548–562. DOI: 10.1016/j.powtec.2018.07.043.
[123]	ZAITSEV Y B, WITTMANN F H. Simulation of crack propagation and failure of concrete [J]. Matériaux et Construction, 1981, 14: 357–365. DOI: 10.1007/BF02478729.
[124]	GIBSON L J, ASHBY M F. Cellular solids: structure and properties [M]. Cambridge: Cambridge University Press, 1997.
[125]	SANTOSA S, WIERZBICKI T. On the modeling of crush behavior of a closed-cell aluminum foam structure [J]. Journal of the Mechanics and Physics of Solids, 1998, 46(4): 645–669. DOI: 10.1016/S0022-5096(97)00082-3.
[126]	LI K, GAO X L, ROY A K. Micromechanics model for three-dimensional open-cell foams using a tetrakaidecahedral unit cell and Castigliano’s second theorem [J]. Composites Science and Technology, 2003, 63(12): 1769–1781. DOI: 10.1016/S0266-3538(03)00117-9.
[127]	CHEON S S, MEGUID S A. Crush behavior of metallic foams for passenger car design [J]. International Journal of Automotive Technology, 2004, 5(1): 17–22. DOI: 10.1109/TVT.2004.823505.
[128]	TUNVIR K, KIM A, CHEON S. Analytical solution for crushing behavior of closed cell al-alloy foam [J]. Mechanics of Advanced Materials and Structures, 2007, 14: 321–327. DOI: 10.1080/15376490600845660.
[129]	冯阳, 梁增友, 吴鸿超, 等. 基于渗流法的泡沫铝细观结构模型研究 [J]. 中北大学学报(自然科学版), 2016, 37(1): 90–96. DOI: 10.3969/j.issn.1673-3193.2016.01.017. FENG Y, LIANG Z Y, WU H C, et al. Research on micro structural model of open-cell aluminum foam based on infiltration casting methods [J]. Journal of North University of China (Natural Science Edition), 2016, 37(1): 90–96. DOI: 10.3969/j.issn.1673-3193.2016.01.017.
[130]	LI L, XUE P, CHEN Y, et al. Insight into cell size effects on quasi-static and dynamic compressive properties of 3D foams [J]. Materials Science & Engineering A, 2015, 636: 60–69. DOI: 10.1016/j.msea.2015.03.052.
[131]	TEKOĞLU C, GIBSON L, PARDOEN T, et al. Size effects in foams: experiments and modeling [J]. Progress in Materials Science, 2011, 56(2): 109–138. DOI: 10.1016/j.pmatsci.2010.06.001.
[132]	王长峰, 郑志军, 虞吉林. 泡沫杆撞击刚性壁的动态压溃模型 [J]. 爆炸与冲击, 2013, 33(6): 587–593. DOI: 10.11883/1001-1455(2013)06-0587-07. WANG C F, ZHENG Z J, YU J L. Dynamic crushing models for a foam rod striking a rigid wall [J]. Explosion and Shock Waves, 2013, 33(6): 587–593. DOI: 10.11883/1001-1455(2013)06-0587-07.
[133]	LI Z Q, ZHANG J J, FAN J H, et al. On crushing response of the three-dimensional closed-cell foam based on Voronoi model [J]. Mechanics of Materials, 2014, 68: 85–94. DOI: 10.1016/j.mechmat.2013.08.009.
[134]	TANG L Q, SHI X P, ZHANG L, et al. Effects of statistics of cell’s size and shape irregularity on mechanical properties of 2D and 3D Voronoi foams [J]. Acta Mechanica, 2014, 225: 1361–1372. DOI: 10.1007/s00707-013-1054-4.
[135]	ZHANG X T, WANG R Q, LIU J X, et al. A numerical method for the ballistic performance prediction of the sandwiched open cell aluminum foam under hypervelocity impact [J]. Aerospace Science and Technology, 2018, 75: 254–260. DOI: 10.1016/j.ast.2017.12.034.
[136]	WEJRZANOWSKI T, SKIBINSKI J, SZUMBARSKI J, et al. Structure of foams modeled by Laguerre–Voronoi tessellations [J]. Computational Materials Science, 2013, 67: 216–221. DOI: 10.1016/j.commatsci.2012.08.046.
[137]	FAN Z G, WU Y G, ZHAO X H, et al. Simulation of polycrystalline structure with Voronoi diagram in Laguerre geometry based on random closed packing of spheres [J]. Computational materials science, 2004, 29(3): 301–308. DOI: 10.1016/j.commatsci.2003.10.006.
[138]	REDENBACH C. Microstructure models for cellular materials [J]. Computational Materials Science, 2009, 44(4): 1397–1407. DOI: 10.1016/j.commatsci.2008.09.018.
[139]	FANG Q, ZHANG J H, ZHANG Y D, et al. A 3D mesoscopic model for the closed-cell metallic foams subjected to static and dynamic loadings [J]. International Journal of Impact Engineering, 2015, 82: 103–112. DOI: 10.1016/j.ijimpeng.2014.10.009.
[140]	FANG Q, ZHANG J H, ZHANG Y D, et al. Mesoscopic investigation of closed-cell aluminum foams on energy absorption capability under impact [J]. Composite Structures, 2015, 124: 409–420. DOI: 10.1016/j.compstruct.2015.01.001.
[141]	ZHENG Z J, WANG C F, YU J L, et al. Dynamic stress-strain states for metal foams using a 3D cellular model [J]. Journal of the Mechanics and Physics of Solids, 2014, 72: 93–114. DOI: 10.1016/j.jmps.2014.07.013.
[142]	ZHANG C Y, TANG L Q, YANG B, et al. Meso-mechanical study of collapse and fracture behaviors of closed-cell metallic foams [J]. Computational Materials Science, 2013, 79: 45–51. DOI: 10.1016/j.commatsci.2013.05.046.
[143]	GREENBERGER M. An a priori determination of serial correlation in computer generated random numbers [J]. Mathematics of Computation, 1961, 15(76): 383–389. DOI: 10.1090/S0025-5718-1961-0144489-8.
[144]	FANG Q, ZHANG J H, CHEN L, et al. An algorithm for the grain-level modelling of a dry sand particulate system [J]. Modelling and Simulation in Materials Science and Engineering, 2014, 22(5): 055021. DOI: 10.1088/0965-0393/22/5/055021.
[145]	MAIRE E, FAZEKAS A, SALVO L, et al. X-ray tomography applied to the characterization of cellular materials. Related finite element modeling problems [J]. Composites Science and Technology, 2003, 63(16): 2431–2443. DOI: 10.1016/S0266-3538(03)00276-8.
[146]	MCDONALD S A, MUMMERY P M, JOHNSON G, et al. Characterization of the three-dimensional structure of a metallic foam during compressive deformation [J]. Journal of Microscopy, 2006, 223(2): 150–158. DOI: 10.1111/j.1365-2818.2006.01607.x.
[147]	JEON I, ASAHINA T, KANG K-J, et al. Finite element simulation of the plastic collapse of closed-cell aluminum foams with X-ray computed tomography [J]. Mechanics of Materials, 2010, 42(3): 227–236. DOI: 10.1016/j.mechmat.2010.01.003.
[148]	SAENGER E H, URIBE D, JÄNICKE R, et al. Digital material laboratory: wave propagation effects in open-cell aluminium foams [J]. International Journal of Engineering Science, 2012, 58: 115–123. DOI: 10.1016/j.ijengsci.2012.03.030.
[149]	陈鹏. 泡沫铝夹芯结构力学性能研究[D]. 哈尔滨: 哈尔滨工业大学, 2013. CHEN P. Research on mechanical properties of aluminum foam sandwich structure [D]. Harbin: Harbin Institute of Technology, 2013.
[150]	SUN Y L, LI Q M, LOWE T, et al. Investigation of strain-rate effect on the compressive behaviour of closed-cell aluminium foam by 3D image-based modelling [J]. Materials and Design, 2016, 89: 215–224. DOI: 10.1016/j.matdes.2015.09.109.
[151]	程振, 方秦, 张锦华, 等. 闭孔泡沫金属三维细观模型建模方法 [J]. 工程力学, 2017, 34(8): 212–221. DOI: 10.6052/j.issn.1000-4750.2016.02.0098. CHENG Z, FANG Q, ZHANG J H, et al. Mesoscopic methodology for the three-dimensional modelling of closed-cell metallic foam [J]. Engineering Mechanics, 2017, 34(8): 212–221. DOI: 10.6052/j.issn.1000-4750.2016.02.0098.
[152]	李侯贞强, 张亚栋, 张锦华, 等. 基于CT的泡沫铝三维细观模型重建及应用 [J]. 北京航空航天大学学报, 2018, 44(1): 160–168. DOI: 10.13700/j.bh.1001-5965.2016.0959. LI H Z Q, ZHANG Y D, ZHANG J H, et al. Reconstruction and application of three-dimensional mesoscopic model of aluminum foam based on CT [J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(1): 160–168. DOI: 10.13700/j.bh.1001-5965.2016.0959.