金属材料层裂再压实的模拟研究

刘军; 孙致远; 张凤国; 王裴

doi:10.11883/bzycj-2021-0262

金属材料层裂再压实的模拟研究

doi: 10.11883/bzycj-2021-0262

刘军^1,,
孙致远¹,
张凤国¹,
王裴^{1, 2}

1.
北京应用物理与计算数学研究所，北京 100094
2.
北京大学应用物理与技术研究中心，北京 100871

基金项目: 于敏基金（TCYM1820-02）；科学挑战专题（TZ2018001）

详细信息

作者简介:
刘　军（1981－　），男，硕士，副研究员，caepcfd@126.com

中图分类号: O368
计量
- 文章访问数: 431
- HTML全文浏览量: 233
- PDF下载量: 96
- 被引次数: 0
出版历程
- 收稿日期: 2021-06-28
- 修回日期: 2021-10-28
- 网络出版日期: 2021-12-29
- 刊出日期: 2022-04-07

Simulation study of the recompression of metal spallation zone

1.
Institute of Applied Physics and Computational Mathematics, Beijing 100094, China
2.
Center for Applied Physics and Technology, Peking University, Beijing 100871, China

摘要

摘要: 激波在自由面卸载后金属内部经常出现层裂现象。若金属内层裂区再次受到冲击加载，则处于拉伸稀疏状态下的金属会逐渐被再次压实为密实介质，直至层裂区消失、再压实过程完成。由于金属层裂区初始拉伸状态的复杂性及再压实后物质状态的不确定性，复杂加载情况下宏观模拟该问题的可靠性验证存在困难。目前，在实验诊断难以准确给出金属层裂区进入再压实过程的初始状态及再压实状态的情况下，具有层裂区内部细节描述能力的直接数值模拟成为了验证宏观模拟可靠性的一种有效手段。首先，在直接数值模拟建模中将金属层裂区初始拉伸状态建模为仅含层裂片、仅含孔洞、同时含有孔洞与层裂片3类情况。然后，通过不同孔隙度、再压实速率、层裂片数及孔洞数下的直接数值模拟，统计得到了对应工况下金属层裂区的再压实状态。最后，在保证直接模拟与宏观模拟具有良好可比性的情况下，对层裂再压实过程进行了宏观建模及模拟分析。分析认为：在宏观网格断裂后处理算法使用全应力置零和温度不变的情况下，宏观模拟能够较好地模拟稀疏区内含层裂片情况下的金属层裂再压实过程及再压实状态；若金属层裂区内部以仅含孔洞的初始状态进入再压实过程，则无论孔洞塌缩是否形成界面喷射，宏观模拟均无法较好模拟该层裂再压实过程及再压实状态。
- 层裂 /
- 再压实 /
- 直接模拟 /
- 宏观模拟 /
- 界面喷射
Abstract: Metal spallation phenomenon often occurs when shock waves are reflected and unloaded on a free surface. If there is a secondary shock wave impact, the metal spallation zone will be compressed again, and the metal in the tensile state will be gradually recompressed into a dense material until the spallation zone disappears. The above process is referred to as the recompression process of the metal spallation zone. The main difficulty of the recompression process simulation is that the initial tensile state of the spallation zone is hard to be determined, and it is difficult to accurately measure the recompaction state experimentally. These bring great difficulties in verifying the reliability of macro-simulations under complex loading. In this case, direct numerical simulations with the ability to describe the internal details of the spallation zone become an effective means to verify the reliability of the macro-simulation. Firstly, in direct simulation modeling, the initial tensile state of the metal spallation zone is set to three situations: containing only spalls, only holes, and both holes and spalls. After that, through direct numerical simulations of different porosity, recompression rate, number of spalls and number of holes, the recompression states of the metal spallation zone under the corresponding working conditions are statistically obtained. Finally, under the condition that the constitutive model and parameters of the direct simulation and macro-simulation have good comparability, macro-modeling and simulation analysis of the spallation recompression process are carried out. The results show that: if there are spalls in the spallation zone, the macro-simulation can better simulate the recompression process and the state of the metal spallation zone when the mesh fracture post-processing algorithm is "set stress to zero and keep temperature constant". If the initial state of the recompression process contains only holes, then macro-simulations cannot well simulate the recompression process and the recompression state no matter whether the hole collapse forms surface material ejections or not.
- spall /
- recompression /
- direct simulation /
- macro-simulation /
- interface ejection

HTML全文

图 1 金属层断裂再压实力学过程示意图

Figure 1. Schematic diagram of the mechanical process of metal spallation and recompression

下载: 全尺寸图片幻灯片

图 2 相同初始孔隙度$ {\alpha }_{0}=1.3 $下不同层裂区建模

Figure 2. Different models of spallation zones with the same initial porosity of $ {\alpha }_{0}=1.3 $

下载: 全尺寸图片幻灯片

图 3 孔洞数量$ {n}_{\mathrm{b}}=12 $下的三维多孔铜1/4模型

Figure 3. Three-dimensional 1/4 model of porous copper with $ {n}_{\mathrm{b}}=12 $

下载: 全尺寸图片幻灯片

图 4 不同孔隙度下多孔铜三维直接模拟与实验结果对比

Figure 4. Comparison of 3D direct simulation and experimental results of porous copper at different porosity

下载: 全尺寸图片幻灯片

图 5 层裂片数$ {n}_{\mathrm{s}\mathrm{p}\mathrm{a}\mathrm{l}\mathrm{l}}=\mathrm{8,20} $下典型时刻的层裂区压缩状态

Figure 5. The compression state of the spallation zone at different times with n_spall = 8, 20

下载: 全尺寸图片幻灯片

图 6 相同初始孔隙度情况下平均密度的变化

Figure 6. Variation of the average density under the same initial porosity

下载: 全尺寸图片幻灯片

图 7 初始孔隙度1.3、再压实速率1.0 km/s，$ {n}_{\mathrm{b}}=12 $情况下的密度图和层裂区平均密度随时间的变化

Figure 7. Results of the density distribution and average density over time by direct simulations with $ {\alpha }_{0}=1.3, $ $ {v}_{0}=1\; {\rm{km}}/{\rm{s}} $, $ {n}_{\rm{b}}=12 $

下载: 全尺寸图片幻灯片

图 8 初始孔隙度1.3、再压实速率0.5 km/s，$ {n}_{\mathrm{b}}=12 $情况下的密度图和层裂区平均密度随时间的变化

Figure 8. Results of the density distribution and average density over time by direct simulations with $ {\alpha }_{0}=1.3, $ $ {v}_{0}=0.5\;\mathrm{k}\mathrm{m}/\mathrm{s} $, ${n}_{\rm{b}}=12 $

下载: 全尺寸图片幻灯片

图 9 初始孔隙度1.3、再压实速率0.3 km/s，$ {n}_{{\rm{b}}}=12 $情况下的密度图和层裂区平均密度随时间的变化

Figure 9. Results of the density distribution and average density over time by direct simulations with $ {\alpha }_{0}=1.3, $ $ {v}_{0}=0.3\;\mathrm{k}\mathrm{m}/\mathrm{s} $, $ {n}_{\rm{b}}=12 $

下载: 全尺寸图片幻灯片

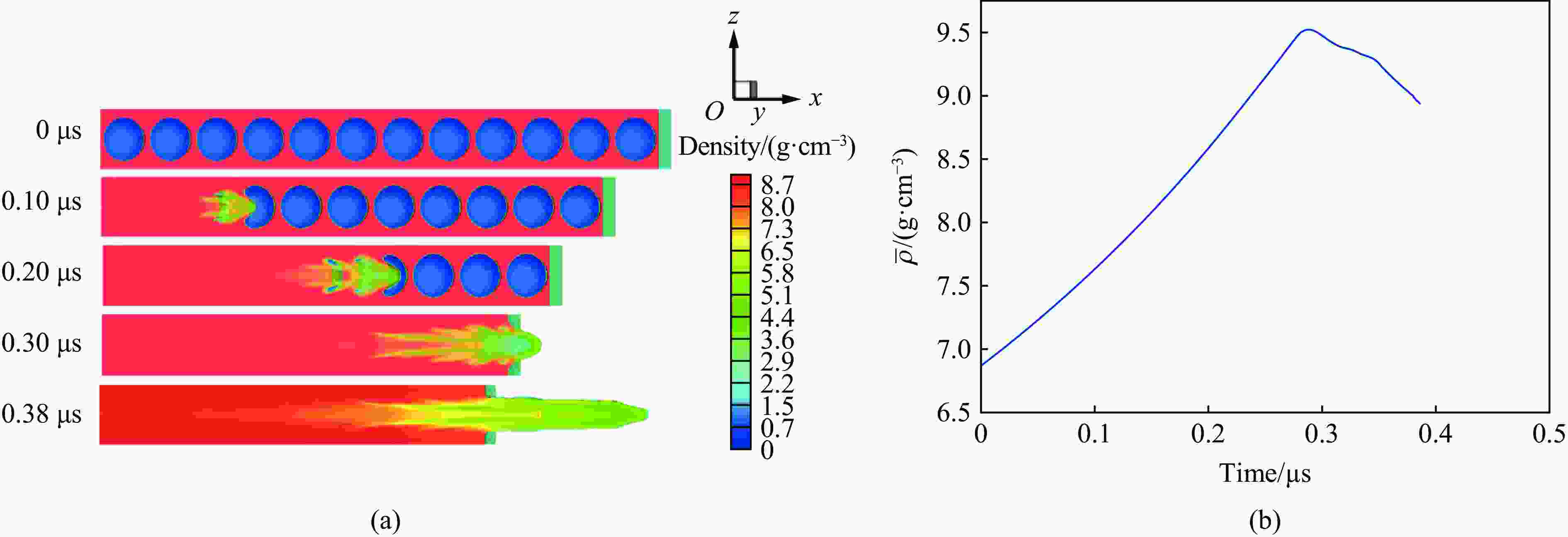
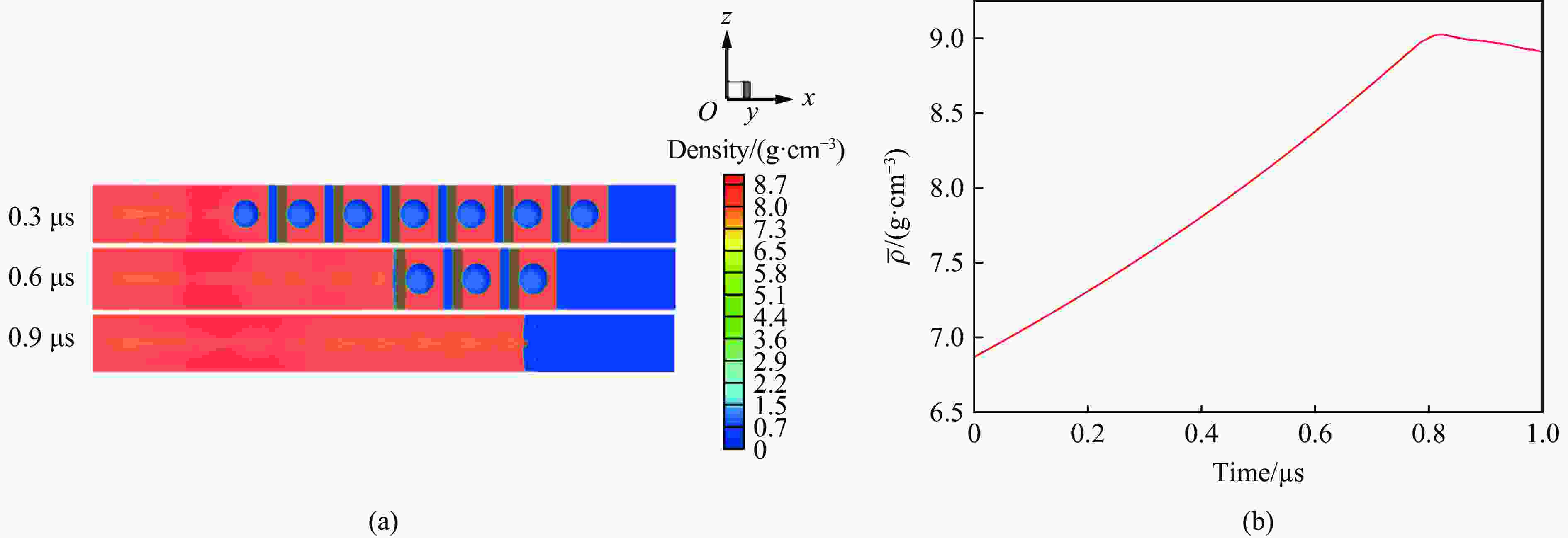
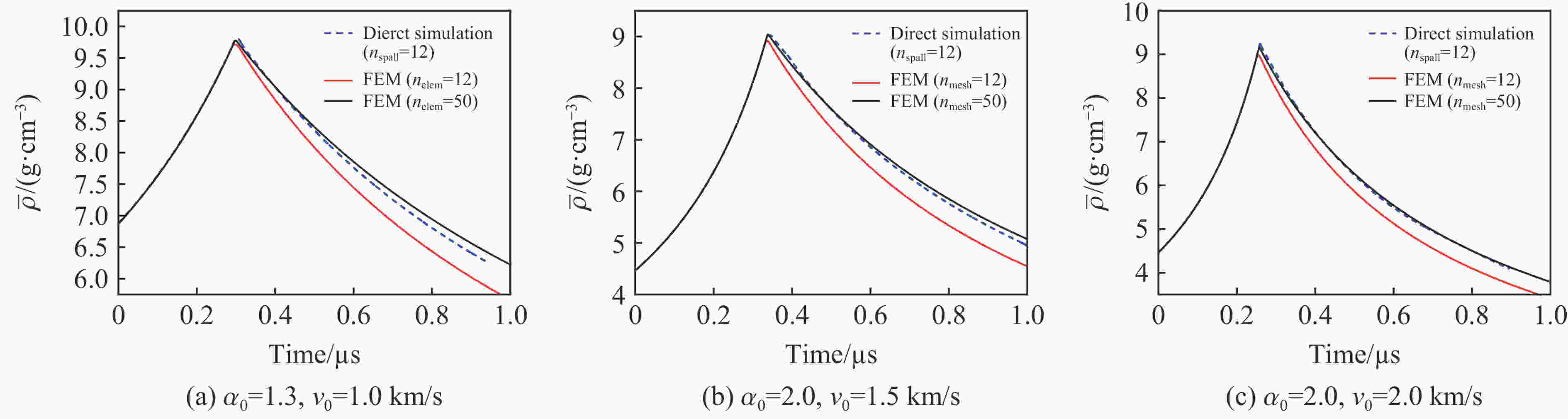
图 10 初始孔隙度1.3、再压实速率1.0 km/s，$ {n}_{\rm{b}}=10 $，${n}_{\rm{spall}}=10 $情况下的密度图和层裂区平均密度随时间的变化

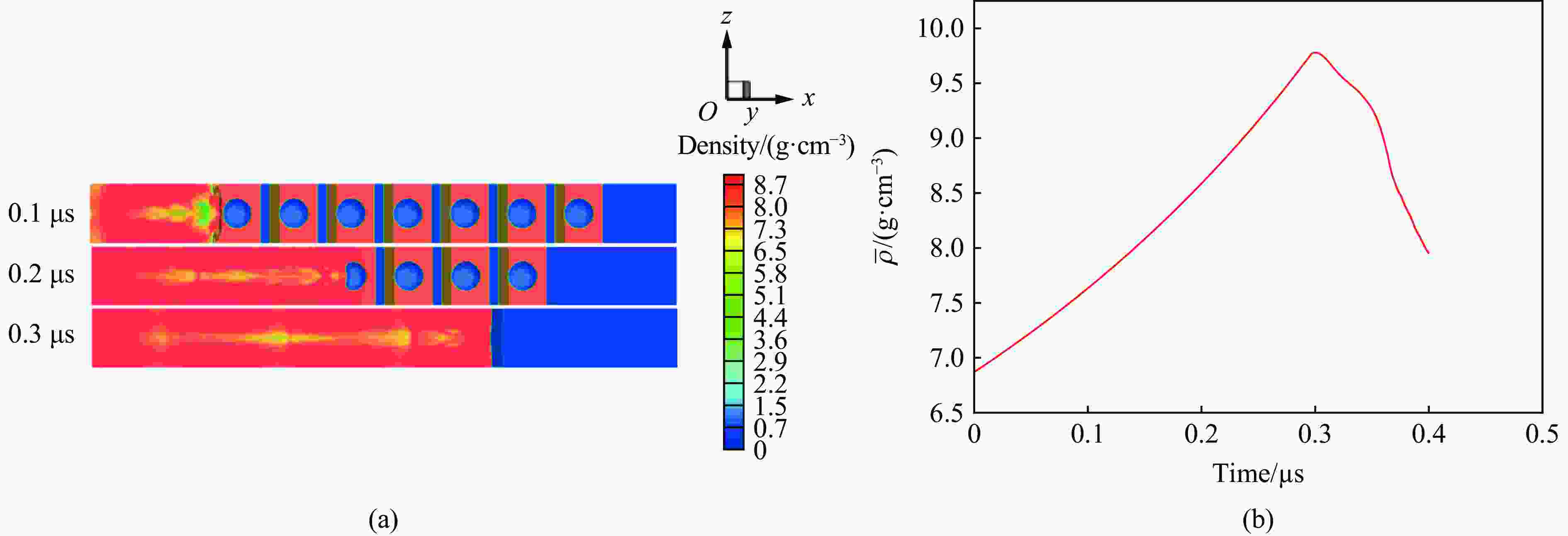
Figure 10. Results of the density distribution and average density over time by direct simulations with $ {\alpha }_{0}=1.3, $ $ {v}_{0}=1\; \mathrm{k}\mathrm{m}/\mathrm{s} $, ${n}_{\rm{b}}=10 , \; {n}_{\rm{spall}}=10 $

下载: 全尺寸图片幻灯片

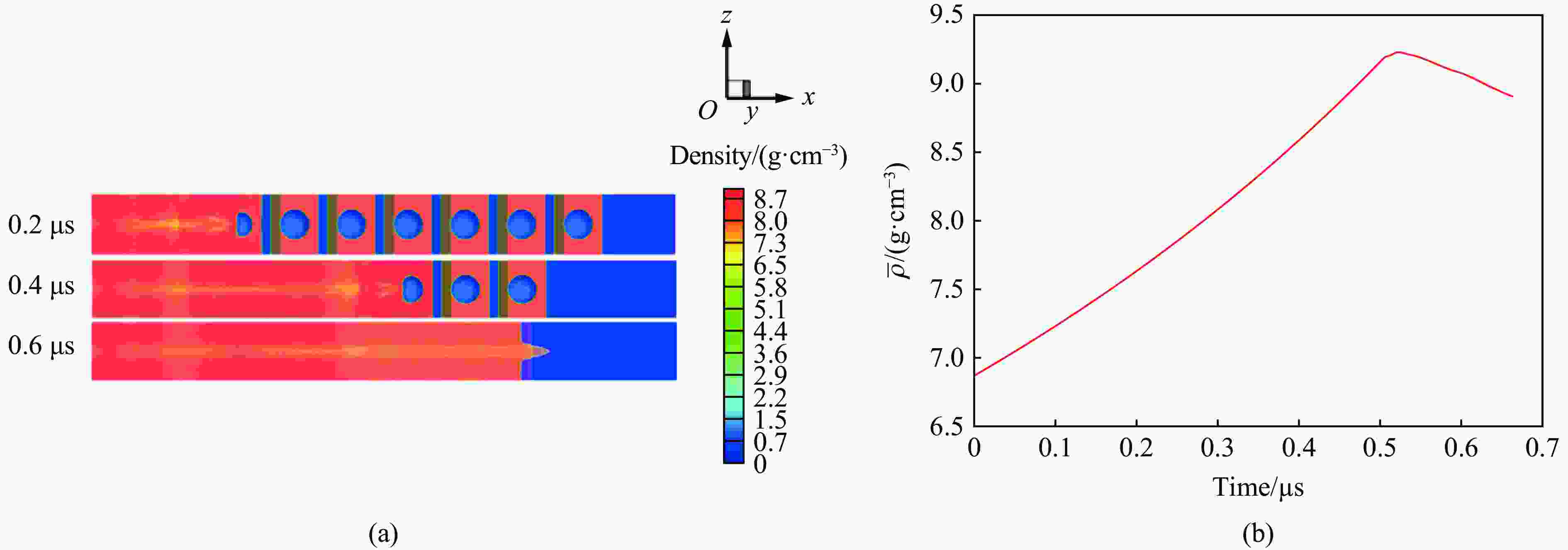
图 11 初始孔隙度1.3、再压实速率0.5 km/s，$ {n}_{\rm{b}}=10 $，${n}_{\rm{spall}}=10 $情况下的密度图和层裂区平均密度随时间的变化

Figure 11. Results of the density distribution and average density over time by direct simulations with $ {\alpha }_{0}=1.3, $ $ {v}_{0}=0.5\;\mathrm{k}\mathrm{m}/\mathrm{s} $, $ {n}_{\rm{b}}=10 , \;{n}_{\rm{spall}}=10 $

下载: 全尺寸图片幻灯片

图 12 初始孔隙度1.3、再压实速率0.3 km/s，$ {n}_{\rm{b}}=10 $，${n}_{\rm{spall}}=10 $情况下的密度图和层裂区平均密度随时间的变化

Figure 12. Results of the density distribution and average density over time by direct simulations with $ {\alpha }_{0}=1.3, $ $ {v}_{0}=0.3\;\mathrm{k}\mathrm{m}/\mathrm{s} $, $ {n}_{\rm{b}}=10 , \;{n}_{\rm{spall}}=10 $

下载: 全尺寸图片幻灯片

图 13 宏观上将层裂区初始均匀剖分为$ {n}_{\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{m}}=20 $

Figure 13. Finite element method is used to simulate the spallation zone described by $ {n}_{\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{m}}=20 $

下载: 全尺寸图片幻灯片

图 14 不同拉伸状态下的层裂区再压实平均密度演化的对比

Figure 14. Comparison of the average recompression density under different tensile conditions

下载: 全尺寸图片幻灯片

图 15 不同孔隙度、不同再压实速度下的宏观模拟与直接模拟的对比

Figure 15. Comparison of the average density obtained from the macro- and direct simulations at different $ {\alpha }_{0} $ and $ {v}_{0} $

下载: 全尺寸图片幻灯片

表 1 金属铜的状态方程参数^[26]

Table 1. The EOS parameters of Cu samples^[26]

ρ₀/(g·cm⁻³)	c₀/(km·s⁻¹)	S₁	S₂	S₃	γ₀	a
8.93	3.94	1.489	0	0	2.02	0.47

下载: 导出CSV

表 2 金属铜的SG本构模型参数^[26]

Table 2. The SG parameters of Cu samples^[26]

$ {Y}_{0}/\mathrm{G}\mathrm{P}\mathrm{a} $	$ {Y}_{\mathrm{m}\mathrm{a}\mathrm{x}}/\mathrm{G}\mathrm{P}\mathrm{a} $	$ \beta $	$ n $	$ b $	$ h $	$ {T}_{\mathrm{m}0}/\mathrm{K} $	$ {\varepsilon }_{00} $	$ {\varepsilon }_{01} $	$ {\varepsilon }_{02} $	$ {\varepsilon }_{03} $	$ {\varepsilon }_{04} $
0.12	0.6	36	0.45	3	3.8×10⁻⁴	1790	−0.1178	−0.2344	7.529	15.26	21.9

下载: 导出CSV

参考文献(27)

[1]	HOLTKAMP D B, CLARK D A, FERM E N, et al. A surver of high explosive-induced damage and spall in selected metals using proton radiography [C]// AIP Conference Proceedings: Shock Compression of Condersed Matter, 2003: 477−482. DOI: 10.1063/1.1780281.
[2]	HOLTKAMP D B, CLARK D A, CRAIN M D, et al. Development of a non-radiographic spall and damage diagnotic [C]// AIP Conference Proceedings, Shock Compression of Condersed Matter, 2003: 473−476. DOI: 10.1063/1.1780280.
[3]	RESSEGUIER T D, SIGNOR L, DRAGON A, et al. Experimental inverstigation of liquid spall in laser shock-loaded tin [J]. Journal of Applied Physics, 2007, 101: 013506. DOI: 10.1063/1.2400800.
[4]	张凤国, 刘军, 王裴, 等. 三角波强加载下延性金属多次层裂破坏问题 [J]. 爆炸与冲击, 2018, 38(3): 659–664. DOI: 10.11883/bzycj-2016-0279. ZHANG F G, LIU J, WANG P, et al. Multi-spall in ductile metal under triangular impulse loading [J]. Explosion and Shock Waves, 2018, 38(3): 659–664. DOI: 10.11883/bzycj-2016-0279.
[5]	贺年丰, 任国武, 陈永涛, 等. 爆轰加载下金属锡层裂破碎数值模拟 [J]. 爆炸与冲击, 2019, 39(4): 042101. DOI: 10.11883/bzycj-2017-0354. HE N F, REN G W, CHEN Y T, et al. Numerical simulation on spallation and fragmentation of tin under explosive loading [J]. Explosion and Shock Waves, 2019, 39(4): 042101. DOI: 10.11883/bzycj-2017-0354.
[6]	杨扬, 彭志强, 郭昭亮, 等. 滑移爆轰条件下高纯铜的层裂行为 [J]. 材料科学与工程学报, 2016, 34(1): 32–37. YANG Y, PENG Z Q, GUO Z L, et al. Spall behaviors of high purity copper under sweeping detonation [J]. Materials Science and Engineering: A, 2016, 34(1): 32–37.
[7]	ANDRIOT P, CHAPRON P, LAMBERT V, et al. Influence of melting on shocked free surface behavior using Doppler laser interferometry and X-ray densitometry [C]// AIP Conference Proceedings: Shock Waves in Condensed Matter, 1983: 277−280. DOI: 10.1016/b978-0-444-86904-3.50065-8.
[8]	REMIOT C, CHAPRON P, DEMAY B. A flash X-ray radiography diagnostic for studying surface phenomena under shock loading [C]// AIP Conference Proceedings, Shock Waves in Condensed Matter, 1994: 1763−1766. DOI: 10.1063/1.46171.
[9]	陈永涛, 胡海波, 汤铁钢, 等. 强冲击加载下铅样品表面微层裂现象诊断 [J]. 中国科学: 物理学力学天文学, 2012, 42: 1076–1085. CEHN Y T, HU H B, TANG T G, et al. Experimental diagnostic of micro-spall fragments on Pb surface under intense shock [J]. Science China: Physics Mechanics & Astronomy, 2012, 42: 1076–1085.
[10]	陈永涛, 任国武, 汤铁钢, 等. 爆轰加载下金属样品的熔化破碎现象诊断 [J]. 物理学报, 2013, 62(11): 116202. DOI: 10.7498/aps.62.116202. CHEN Y T, REN G W, TANG T G, et al. Experimental diagnostic of melting fragments under explosive loading [J]. Acta Physica Sinica, 2013, 62(11): 116202. DOI: 10.7498/aps.62.116202.
[11]	CHEN Y T, REN G W, TANG T G, et al. Experimental study of micro-spalling fragmentation from melted lead [J]. Shock Waves, 2016, 26: 221–225. DOI: 10.1007/s00193-015-0601-4.
[12]	张崇玉, 胡海波, 王翔. 铅飞层中斜冲击波对碰马赫反射行为实验研究 [J]. 爆炸与冲击, 2019, 39(4): 043102. ZHANG C Y, HU H B, WANG X, et al. Experimental study of Mach reflection induced by collision of oblique shock waves in a lead plate [J]. Explosion and Shock Waves, 2019, 39(4): 043102.
[13]	XIANG M Z, HU H B, CHEN J. Molecular dynamics studies of thermal dissipation during shock induced spalling [J]. Journal of Applied Physics, 2013, 113(16): 163507–6. DOI: 10.1063/1.4821341.
[14]	SEAMAN L, CURRAN D R, SHOCKEY D A. Computational models for ductile and brittle fracture [J]. Journal of Applied Physics, 1976, 47(11): 4814–4826. DOI: 10.1063/1.322523.
[15]	GURSON A L. Continuum theory of ductile rupture by void nucleation and growth: Part Ⅰ: yield criteria and flow rules for porous ductile media [J]. Journal of Engineering Materials and Technology, 1977, 99(1): 2–15. DOI: 10.1115/1.3443401.
[16]	TONKS D L, ZUREK A K, THISSELL W R. Void coalescence model for ductile damage [C]// AIP Conference Proceedings: Shock Compression of Condensed Matter. 2002: 611–614. DOI: 10.1063/1.1483613.
[17]	MOLINARI A, WRIGHT T. A physical model for nucleation and early growth of voids in ductile materials under dynamic loading [J]. Journal of the Mechanics and Physics of Solids, 2005, 53(7): 1476–1504. DOI: 10.1016/j.jmps.2005.02.010.
[18]	HERRMANN W. Constitutive equation for the dynamic compaction of ductile porous materials [J]. Journal of Applied Physics, 1969, 40(6): 2490–9. DOI: 10.1063/1.1658021.
[19]	CARROLL M M, HOLT A C. Static and dynamic pore-collapse relations for ductile porous materials [J]. Journal of Applied Physics, 1972, 43(4): 1626–36. DOI: 10.1063/1.1661372.
[20]	WUENNEMANN K, COLLINS G S, MELOSH H J. A novel porosity model for use in hydrocode simulations: 20050180812 [R].USA: Lunar and Planetary Science Ⅹ Ⅹ Ⅹ Ⅵ, Part 21, 2005.
[21]	COLLINS G S, MELOSH H J, WUNNEMANN K, et al. Improvements to the ε-α porous compaction model for simulation impacts into high-porosity solar system objects [J]. International Journal of Impact Engineering, 2011, 38: 434–439. DOI: 10.1016/j.ijimpeng.2010.10.013.
[22]	何长江, 于志鲁, 冯其京. 高速碰撞的三维欧拉数值模拟方法 [J]. 爆炸与冲击, 1999, 19(3): 216–221. HE C J, YU Z L, FENG Q J. 3D Eulerian numerical simulation method of high speed impact [J]. Explosion and Shock Waves, 1999, 19(3): 216–221.
[23]	冯其京, 郝鹏程, 杭义洪, 等. 聚能装药的欧拉数值模拟 [J]. 爆炸与冲击, 2008, 28(2): 138–143. DOI: 10.11883/1001-1455(2008)02-0138-06. FENG Q J, HAO P C, HANG Y H, et al. Eulerian numerical simulation of a shaped charge [J]. Explosion and Shock Waves, 2008, 28(2): 138–143. DOI: 10.11883/1001-1455(2008)02-0138-06.
[24]	刘军, 王裴, 王言金. L-R两步欧拉方法在铝材料微喷射中的应用 [J]. 高压物理学报, 2014, 28(3): 346–352. DOI: 10.11858/gywlxb.2014.03.013. LIU J, WANG P, WANG Y J. Application of L-R two-step Euler method to micro ejection of aluminum [J]. Chinese Journal of High Pressure Physics, 2014, 28(3): 346–352. DOI: 10.11858/gywlxb.2014.03.013.
[25]	HE A M, LIU J, LIU C, WANG P. Numerical and theoretical investigation of jet formation in lastic-plastic solids [J]. Journal of Applied Physics, 2018, 124: 185902. DOI: 10.1063/1.5051527.
[26]	STEINBERG D J. Equation of state and strength properties of selected materials: UCRL-MA-106439 [R]. USA: Lawrence Livermore National Laboratory, 1991.
[27]	WHIRLEY R G, ENGELMANN B E. DYNA2D: a nonlinear, explicit, two dimensional finite element code for solid mechanics: UCRL-MA-110630 [R]. USA : NASA STI Technical Report, 1992.