Numerical modeling and application of shock wave of free-field air explosion
-
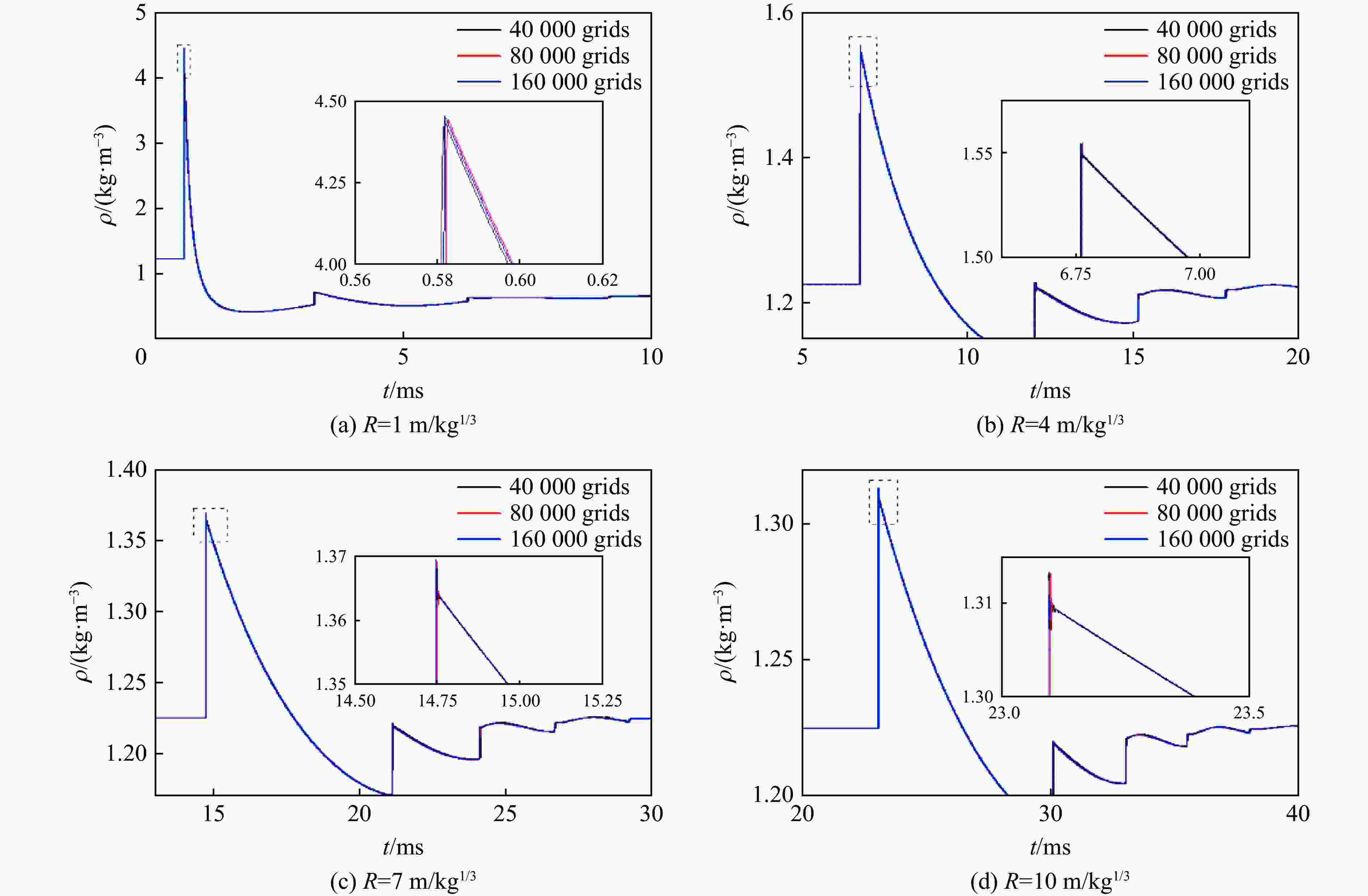
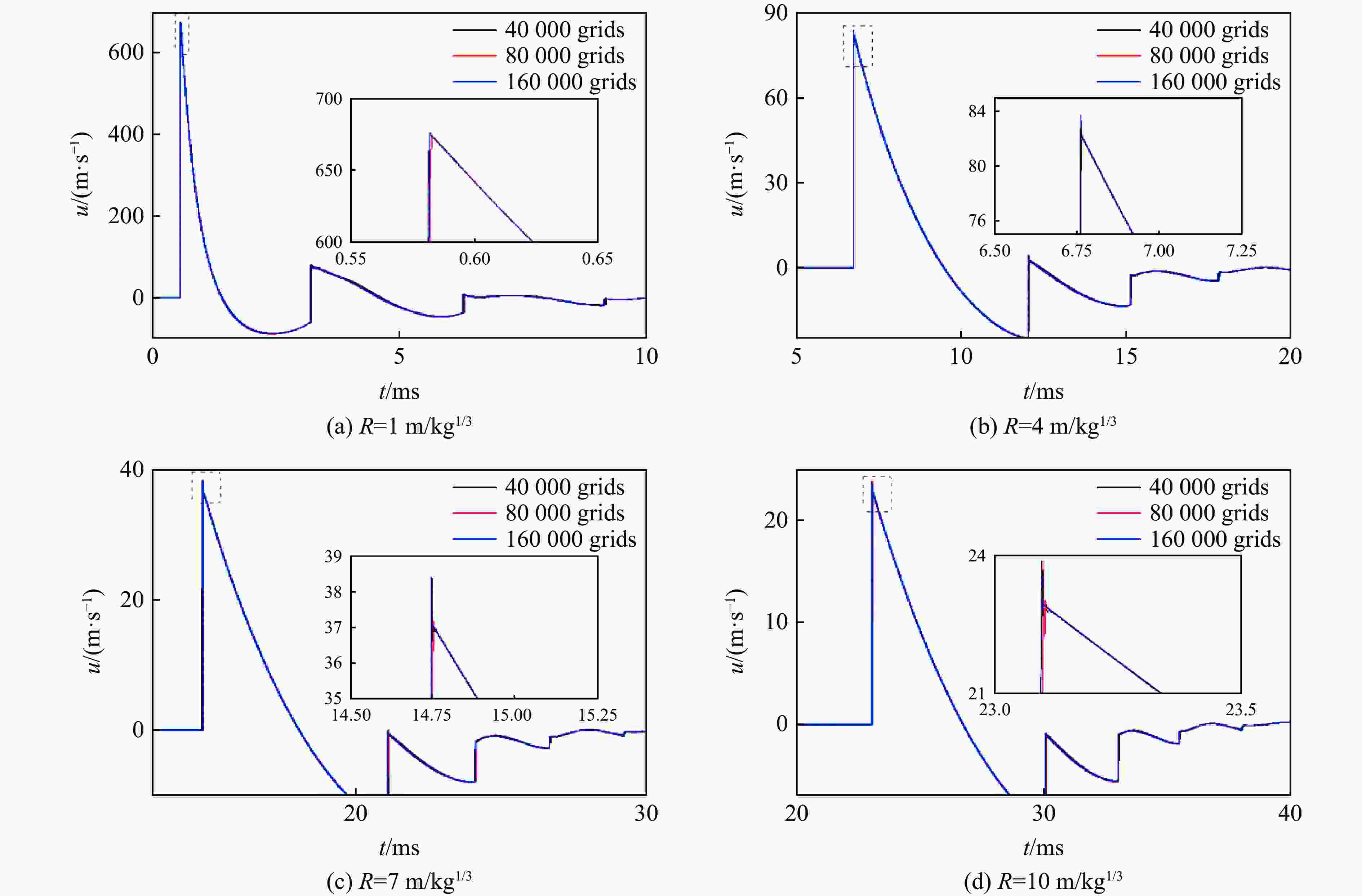
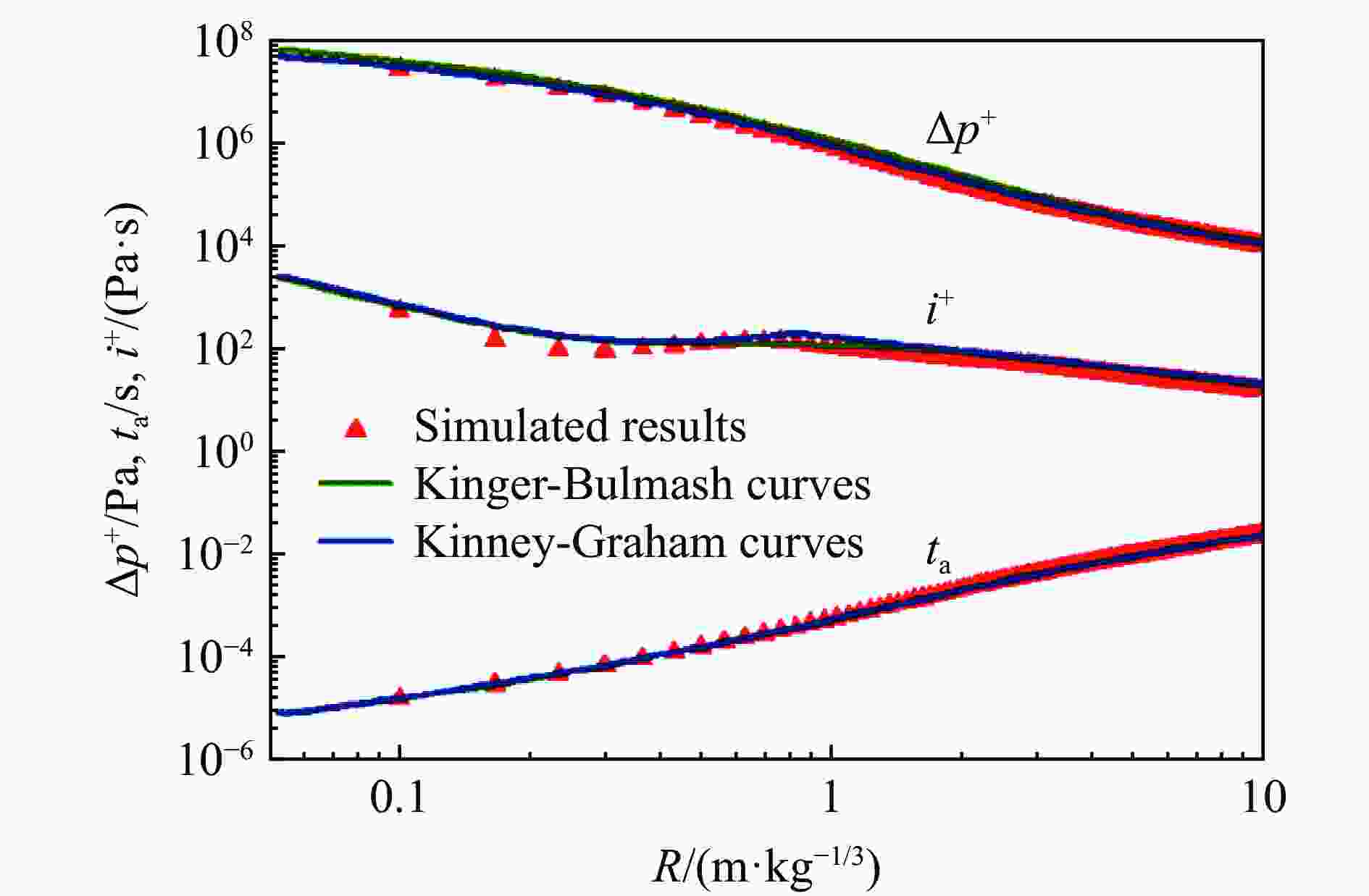
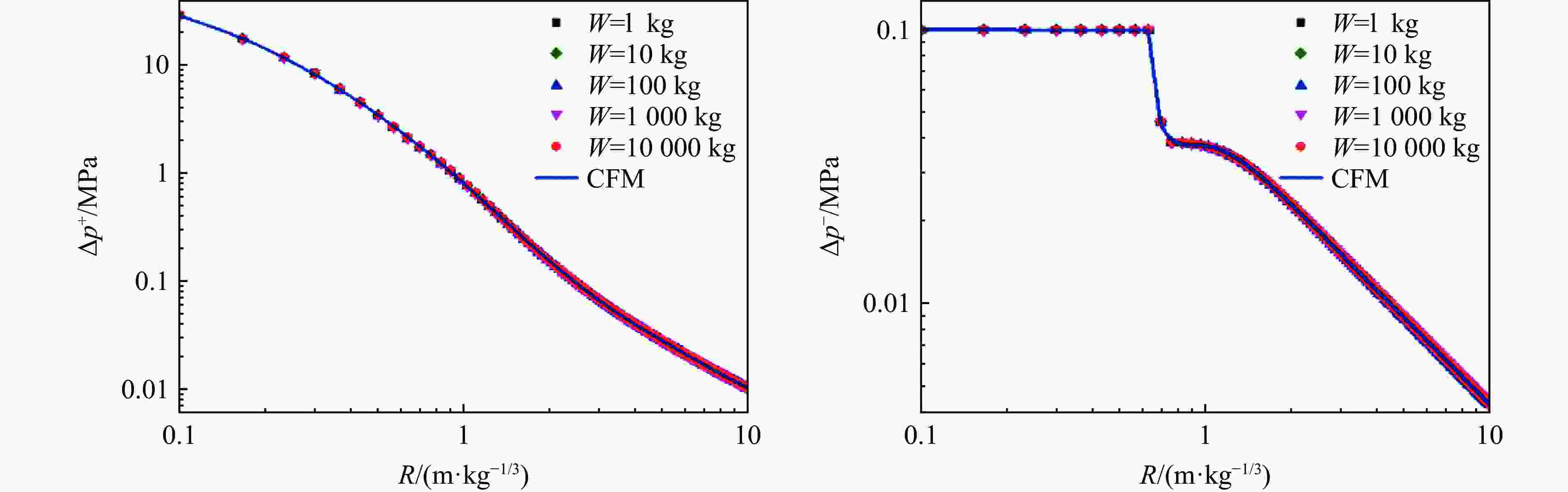
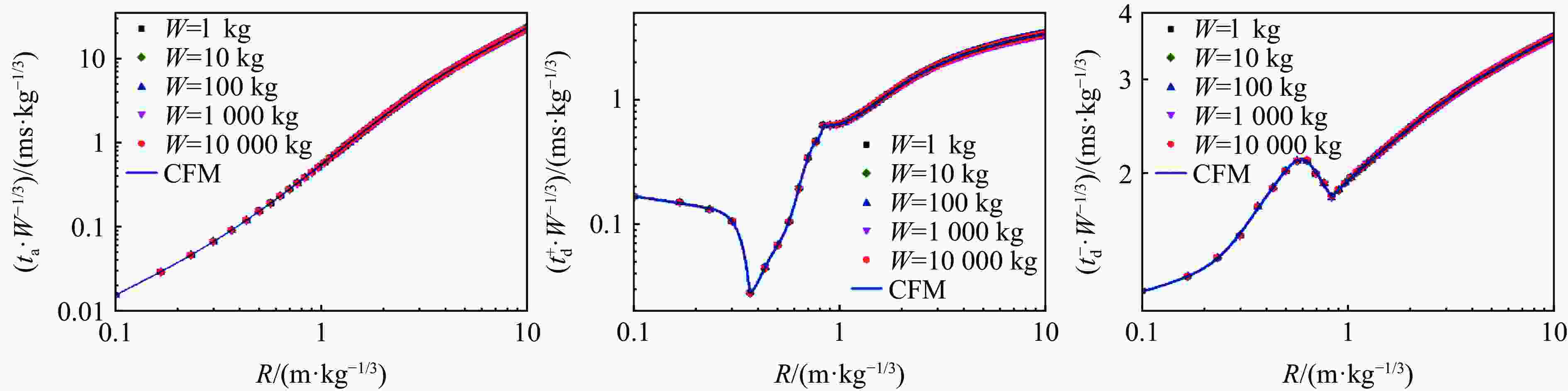
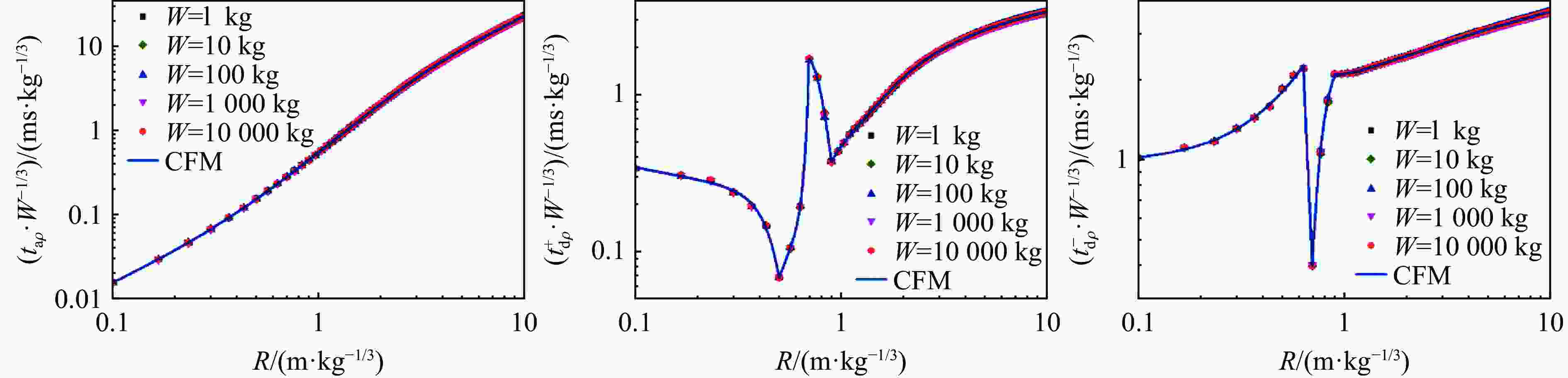
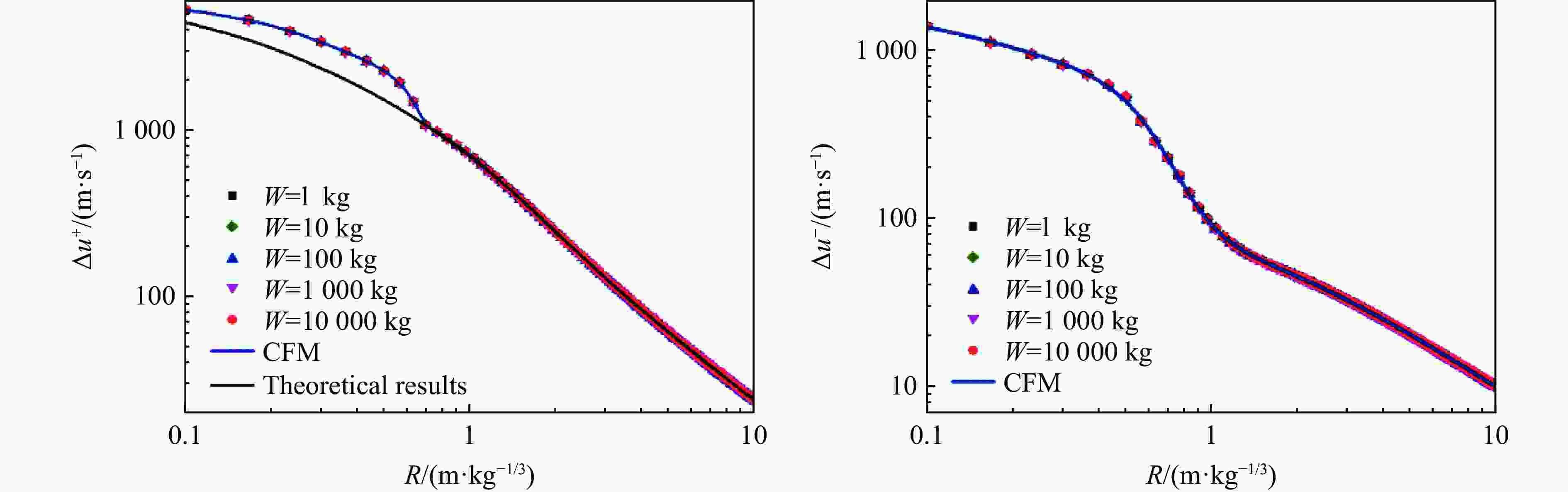
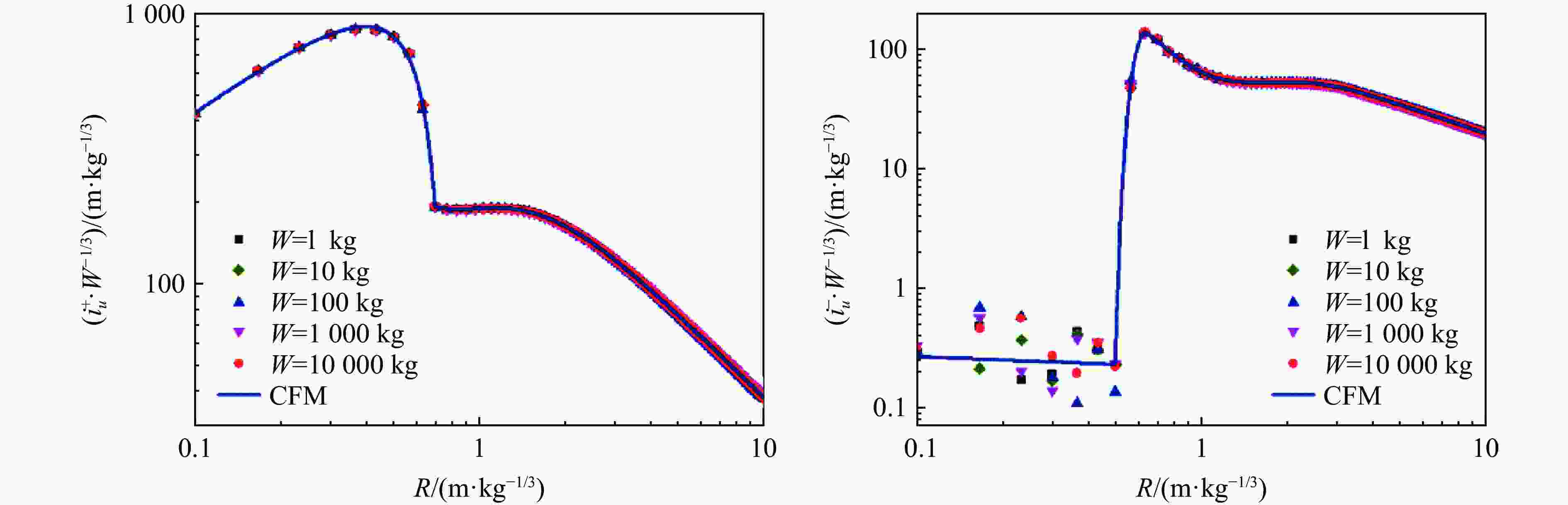
摘要: 为建立描述任意时刻、距离下空气自由场爆炸波冲击波压力、密度、粒子速度的经验公式，支撑复杂场景下冲击波载荷的快速计算，采用一维精细数值模拟的方法计算了不同比例距离下的压力、密度、粒子速度时程，并利用曲线拟合方法得到了正相超压峰值等22个冲击波参数与比例距离关系的经验公式，采用改进修正Friedlander方程建立了冲击波压力、密度、粒子速度随时间变化的关系式；利用爆炸冲击波地面反射和建筑后绕射两个典型工况，阐释了提出模型的应用场景，并与试验、数值模拟结果对比。结果表明：压力、密度、粒子速度随比例距离、时间变化的经验关系与数值模拟结果基本吻合；爆炸冲击波地面反射和建筑后绕射两个典型工况下，理论计算与数值模拟的压力云图基本吻合，在相同硬件条件下，理论计算耗时仅为千万级网格数值模拟的5%左右，在计算速度上有明显的优越性。
-
关键词:
- 自由场爆炸 /
- Friedlander 方程 /
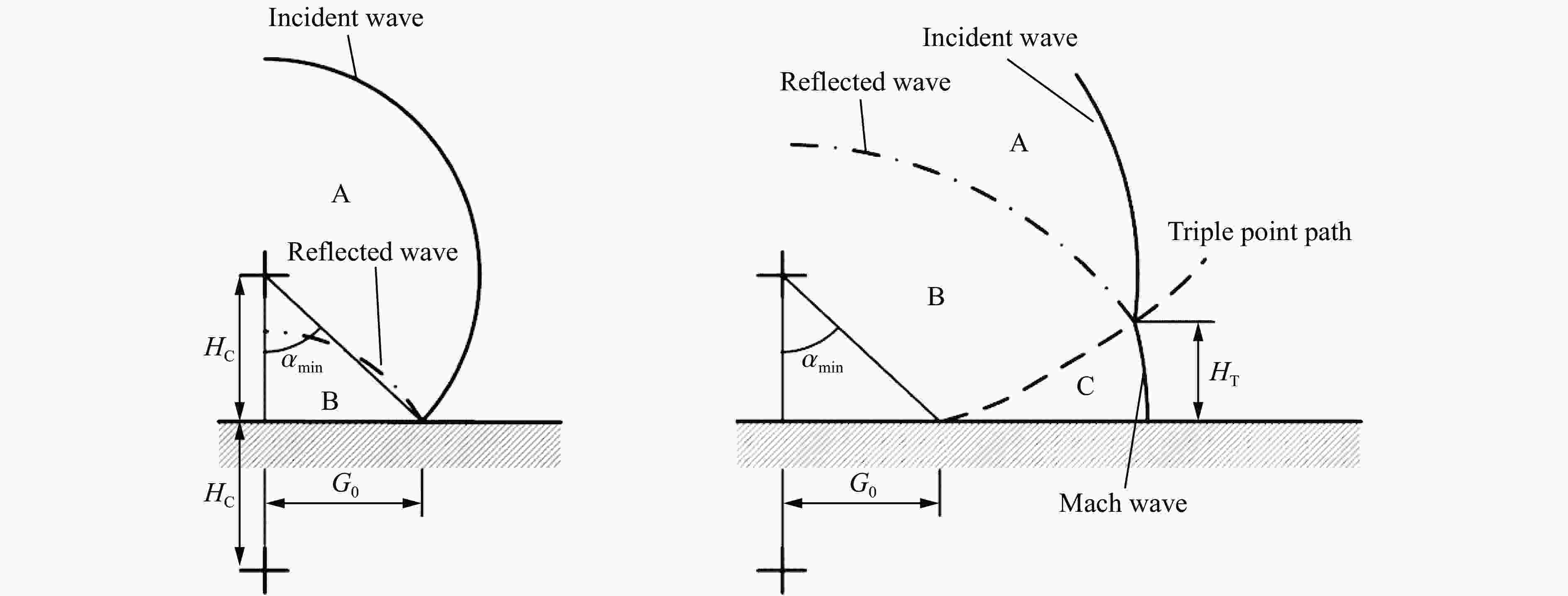
- 冲击波反射 /
- 冲击波绕射
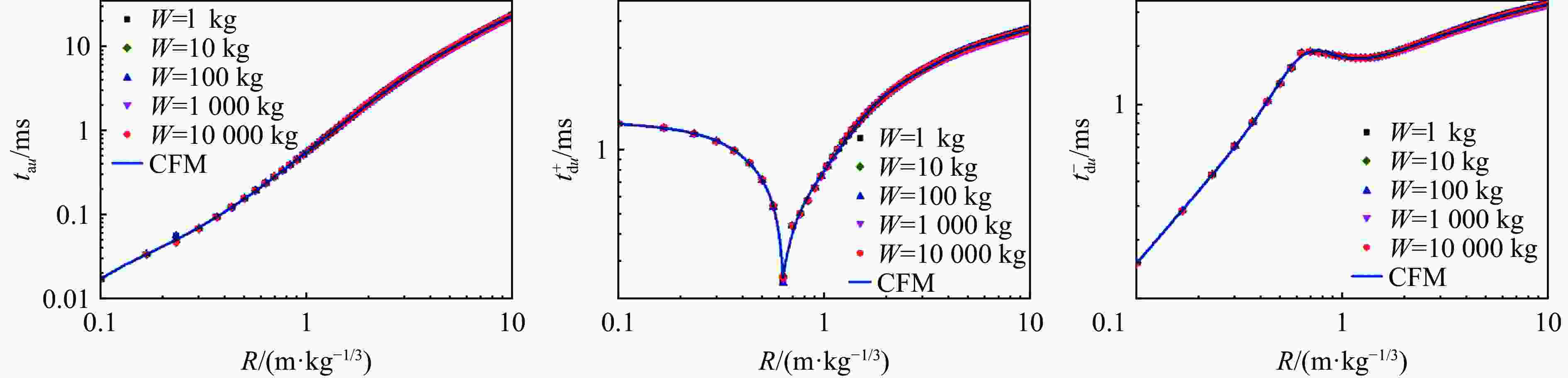
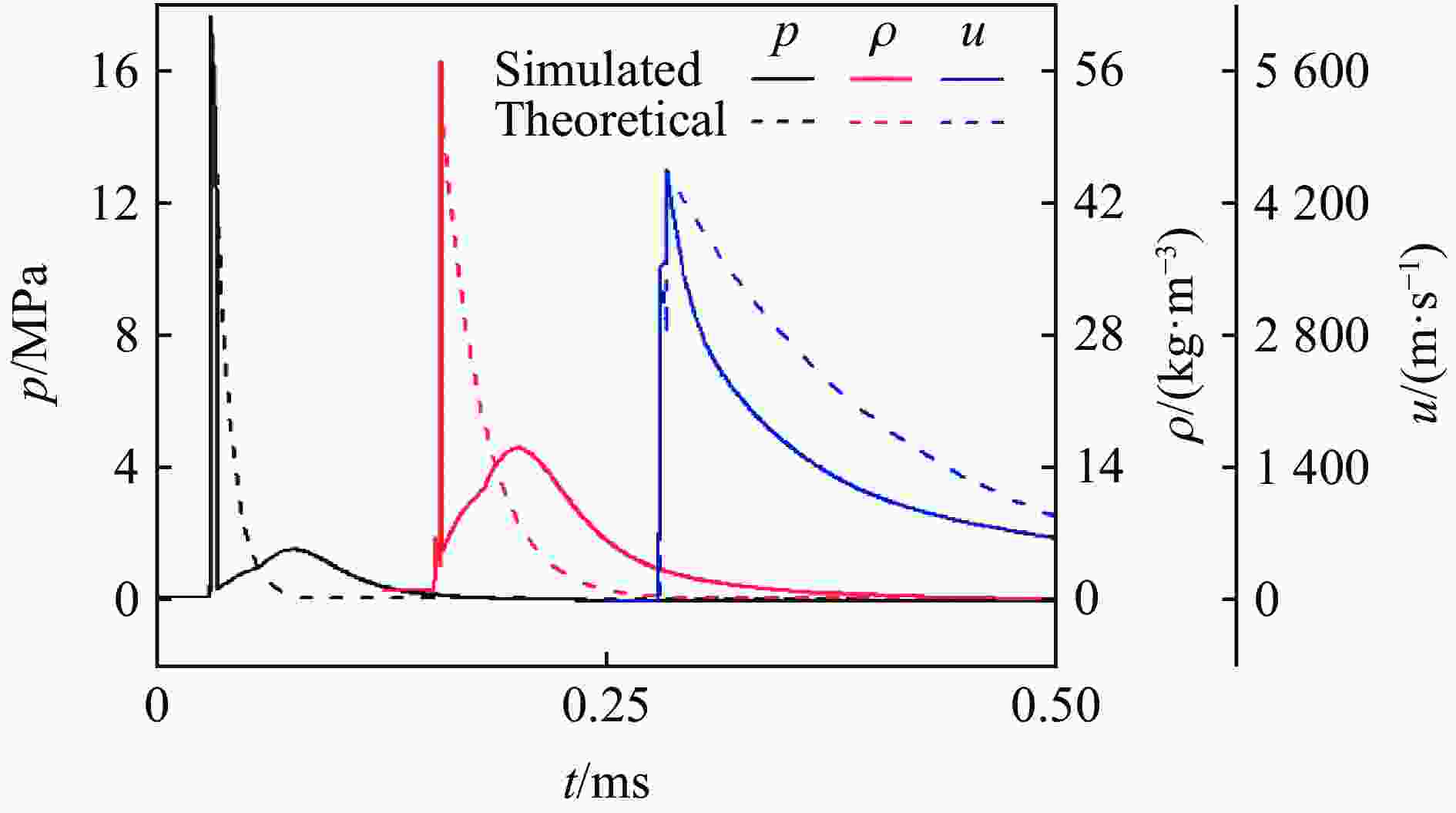
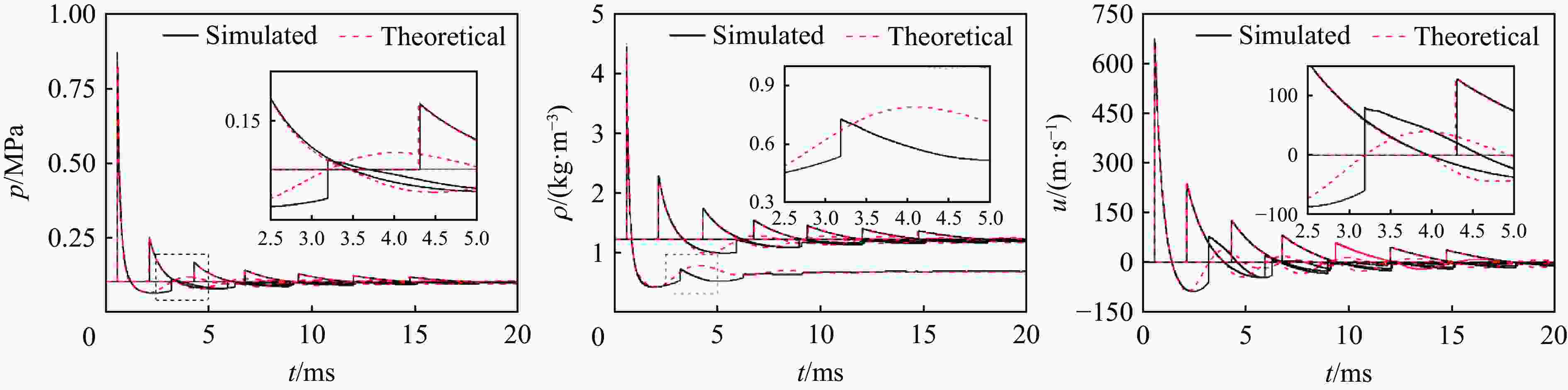
Abstract: In order to establish an empirical formula to describe the pressure, density and particle velocity of the blast wave at any time and distance in free field, and to support the theoretical calculation of shock wave loading in complex scenarios, the pressure, density and particle velocity histories at different scaled distances were obtained by one-dimensional numerical simulation. The empirical formula of the relationship between shock wave parameters and specific distance was obtained by using the curve fitting method, and the relationship of shock wave pressure, density and particle velocity with time were established by the improved modified Friedlander equation. Based on the two typical scenarios of ground reflection and rear diffraction of explosive shock wave, the application of the proposed model was explained. And the accuracy of the proposed model and related theoretical methods are verified by comparison with the experimental and numerical simulation results. The results show that, within the range from 0.1 to 10 m/kg1/3, the relation of scaled distance and shock wave parameters obtained by curve fitting method are highly consistent with the numerical simulation results, which R2 values are higher than 0.999. The developed basic shock wave parameters time-history curves can ensure the peak value and the maximum impulse is equal to the numerical simulation results in near-field. And in the middle and far-field, the developed time-history curves are in good agreement with the numerical simulation results. Under two typical conditions: ground reflection of explosive shock wave and rear diffraction shock wave around building, the theoretical results are in good agreement with the contour diagram of numerical simulation results. Under the same hardware condition, the time-consuming of theoretical calculation is only about 5% in the numerical simulation of 10 million-level grid, which shows that the method has obvious superiority in calculating speed.-
Key words:
- free-field explosion /
- Friedlander equation /
- shock reflection /
- shock diffraction
-
图 1 不同网格数量下的压力时程数值模拟结果
Figure 1. Numerical result of pressure changing with different grid quantity
图 2 不同网格数量下的密度时程数值模拟结果
Figure 2. Numerical result of density with different grid quantity
图 3 不同网格数量下的粒子速度时程数值模拟结果
Figure 3. Numerical result of particle velocity with different grid quantity
图 8 中止密度和超密度峰值与比例距离关系
Figure 8. Relationship of cut suspend density and peak density with scaled distance
图 11 粒子速度峰值与比例距离关系
Figure 11. Relationship between peak particle velocity and scaled distance
图 12 速度积分与比例距离关系
Figure 12. Relationship between velocity integral and scaled distance
图 14 R=0.17 m/kg1/3处冲击波基本参数理论及数值模拟时程
Figure 14. Simulated and theoretical basic shock wave parameter histories at R=0.17 m/kg1/3
图 15 冲击波基本参数理论及数值模拟时程曲线
Figure 15. Simulated and theoretical basic parameter history of shock waves
图 16 空爆地面反射实验布置
Figure 16. Experimental arrangement of ground reflection of air explosion
图 20 爆炸冲击波建筑后绕射实验布置图
Figure 20. Experimental arrangement of explosion shock wave diffraction behind the building corner
图 21 冲击波绕射理论计算空间划分示意图
Figure 21. Schematic diagram of space division of shock wave diffraction theoretical calculation
图 22 z=1.35 m平面理论与数值计算结果的压力分布云图
Figure 22. Theoretical and simulated results of pressure contours on the z=1.35 m plane
密度/(kg·m−1/3) E0/GPa A/GPa B/GPa R1 R2 ω 1630 7.0 373.8 3.75 4.15 0.9 0.35 
下载: 导出CSV
表 2 各测点的超压峰值（Δ
$ p $ +）和冲量极值（$i $ +）理论结果与数值模拟、试验结果对比Table 2. Comparison of peak overpressure (Δp+) and maximum impulse (i+) between theoretical values and experimental results, simulation results of each gauges
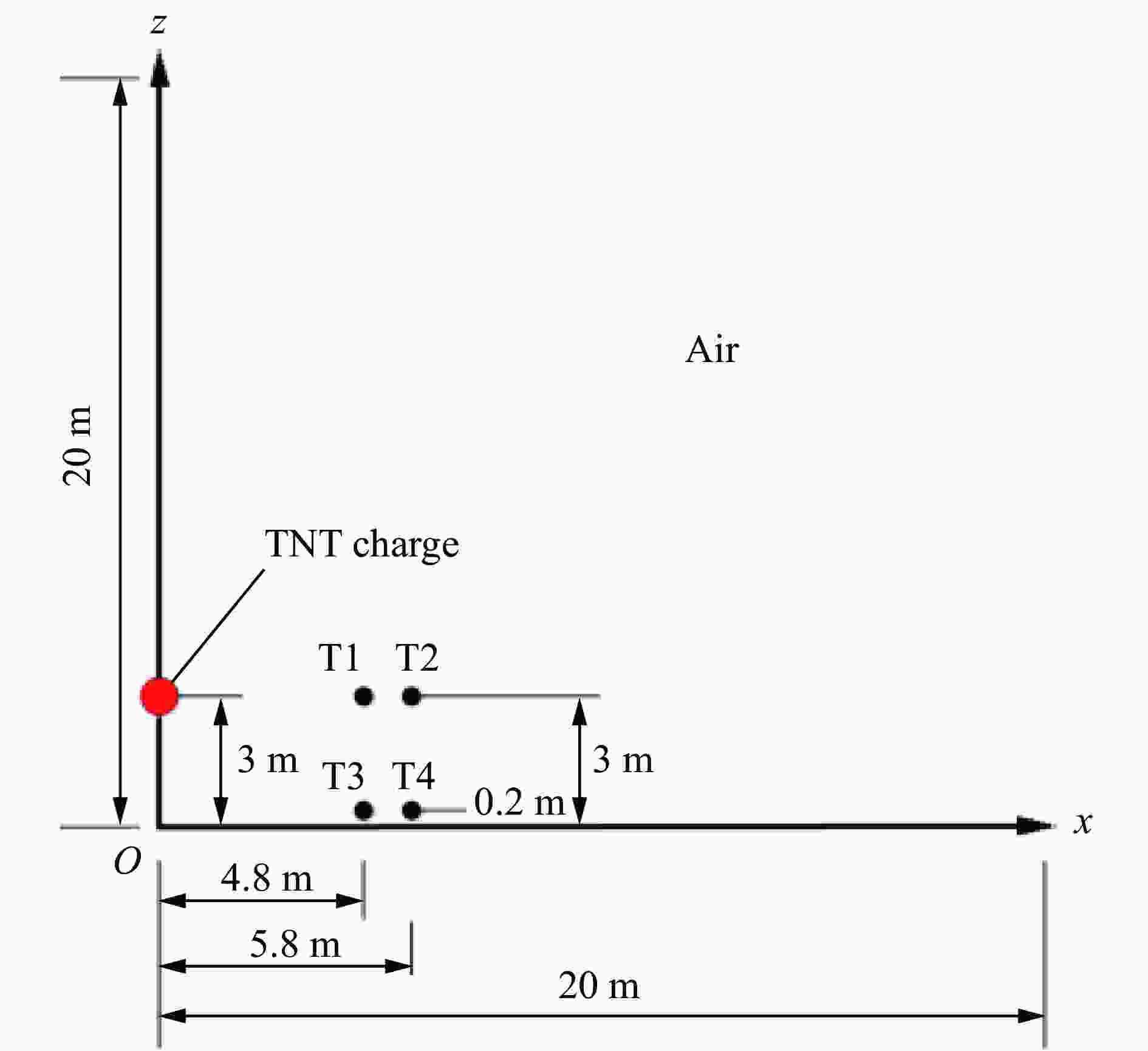
测点 δ1(Δp+)/% δ2(Δp+)/% δ3(Δp+)/% δs(Δp+)/% δ1(i+)/% δ1(i+)/% δ1(i+)/% δ1(i+)/% T1 23.5 19.5 19.3 8.6 2.4 39.6 31.7 0.8 T3 30.0 − − 8.6 21.8 − − 2.1 T4 − 23.3 − 6.9 − 23.1 − 4.8 T5 − − 0.4 7.8 − − 38.4 6.0 注：δk为理论结果相对于第k次（k=1、2、3）试验结果的误差，δs为理论结果相对于模拟结果的误差。
下载: 导出CSV
-
[1] BANGASH M Y H, BANGASH T. Explosion-resistant buildings, design, analysis, and case studies [M]. Berlin: Springer, 2006. DOI: 10.1007/3-540-31289-7. [2] CORMIE D, MAYS G, SMITH P. Blast effects on buildings [M]. 3rd ed. London: ICE Publishing, 2020. [3] ZHOU Q, HE H G, LIU S F, et al. Blast resistance evaluation of urban utility tunnel reinforced with BFRP bars [J]. Defence Technology, 2021, 17(2): 512–530. DOI: 10.1016/j.dt.2020.03.015. [4] HUANG X, BAO H R, HAO Y F, et al. Damage assessment of two-way RC slab subjected to blast load using mode approximation approach [J]. International Journal of Structural Stability and Dynamics, 2017, 17(1): 1750013. DOI: 10.1142/S0219455417500134. [5] LANGENDERFER M, WILLIAMS K, DOUGLAS A, et al. An evaluation of measured and predicted air blast parameters from partially confined blast waves [J]. Shock Waves, 2021, 31(2): 175–192. DOI: 10.1007/s00193-021-00993-0. [6] TAN C M M. Rapid estimation of building damage by conventional weapons [M]. US: Naval Postgraduate School, 2014. [7] BOGOSIAN D, FERRITTO J, SHI Y J. Measuring uncertainty and conservatism in simplified blast models [C]// Proceedings of the 30th Explosives Safety Seminar. Atlanta, Georgia, US, 2002. [8] 马涛. 空气中爆炸波快速算法研究 [D]. 长沙: 国防科学技术大学, 2014.MA T. The study for fast computation of blast wave in air [D]. Changsha: National University of Defense Technology, 2014. [9] NEEDHAM C E. Blast waves [M]. 2nd ed. Cham: Springer, 2018. DOI: 10.1007/978-3-319-65382-2. [10] US Army Corps of Engineers. Structures to resist the effects of accidental explosions: UFC 3-340-02 [S]. USA: Department of Defense of USA, 2008. [11] DUSENBERRY D, SCHMIDT J, HOBELMANN P, et al. Blast protection of buildings: ASCE/SEI 59-11 [S]. USA: American Society of Civil Engineers, 2011. DOI: 10.1061/9780784411889. [12] ABRAHAM J, STEWART C. Shock 2.0 theory manual: TR-NAVFAC ESC-CI-1101 [M]. 2011. [13] 杨亚东, 李向东, 王晓鸣. 长方体密闭结构内爆炸冲击波传播与叠加分析模型 [J]. 兵工学报, 2016, 37(8): 1449–1455. DOI: 10.3969/j.issn.1000-1093.2016.08.016.YANG Y D, LI X D, WANG X M. An analytical model for propagation and superposition of internal explosion shockwaves in closed cuboid structure [J]. Acta Armamentarii, 2016, 37(8): 1449–1455. DOI: 10.3969/j.issn.1000-1093.2016.08.016. [14] Numerics Software. Fl-blast v1.1 theory manual [M]. Germany: Numerics Software, 2017. [15] FRANK S, FRANK R, HURLEY J. Fast-running model for arbitrary room airblast [C]// Proceedings of the International Symposium for the Interaction of the Effects of Munitions on Structures (ISIEMS 12.1). Orlando, FL, 2007. [16] CAMPIDELLI M, VIOLA E. An analytical–numerical method to analyze single degree of freedom models under airblast loading [J]. Journal of Sound and Vibration, 2007, 302(1/2): 260–286. DOI: 10.1016/j.jsv.2006.11.024. [17] 张玉涛, 田玄鑫, 孙贝生, 等. 爆炸冲击波载荷特征对冲击响应谱影响规律研究 [J]. 舰船科学技术, 2019, 41(6): 48–52. DOI: 10.3404/j.issn.1672-7469.2019.06.010.ZHANG Y T, TIAN X X, SUN B S, et al. Research on the influence of the wave spectrum characteristics on the shock response of explosion shock load [J]. Ship Science and Technology, 2019, 41(6): 48–52. DOI: 10.3404/j.issn.1672-7469.2019.06.010. [18] XIAO W F, ANDRAE M, GEBBEKEN N. Air blast TNT equivalence factors of high explosive material PETN for bare charges [J]. Journal of Hazardous Materials, 2019, 377: 152–162. DOI: 10.1016/j.jhazmat.2019.05.078. [19] XIAO W F, ANDRAE M, GEBBEKEN N. Air blast TNT equivalence concept for blast-resistant design [J]. International Journal of Mechanical Sciences, 2020, 185: 105871. DOI: 10.1016/j.ijmecsci.2020.105871. [20] KINNEY G F, GRAHAM K J. Explosive shocks in air [M]. 2nd ed. Berlin: Springer, 1985. DOI: 10.1007/978-3-642-86682-1. [21] BAKER W E. 空中爆炸 [M]. 江科, 译. 北京: 原子能出版社, 1982.BAKER W E. Explosions in air [M]. JIANG K, trans. Beijing: Atomic Energy Press, 1982. [22] 程祥, 杨明, 郭亚丽, 等. 修正的Friedlander方程指数衰减因子 [J]. 爆炸与冲击, 2009, 29(4): 425–428. DOI: 10.11883/1001-1455(2009)04-0425-04.CHENG X, YANG M, GUO Y L, et al. Analysis on an exponential attenuation factor in the modified Friedlander equation by overpressure tests [J]. Explosion and Shock Waves, 2009, 29(4): 425–428. DOI: 10.11883/1001-1455(2009)04-0425-04. [23] 杨科之, 刘盛. 空气冲击波传播和衰减研究进展 [J]. 防护工程, 2020, 42(3): 1–10. DOI: 10.3969/j.issn.1674-1854.2020.03.001.YANG K Z, LIU S. Progress of research on propagation and attenuation of air blast [J]. Protective Engineering, 2020, 42(3): 1–10. DOI: 10.3969/j.issn.1674-1854.2020.03.001. [24] RANDERS-PEHRSON G, BANNISTER K A. Airblast loading model for DYNA2D and DYNA3D: ARL-TR-1310 [R]. USA: Army Research Laboratory, 1997. [25] XUE Z Q, LI S P, XIN C L, et al. Modeling of the whole process of shock wave overpressure of free-field air explosion [J]. Defence Technology, 2019, 15(5): 815–820. DOI: 10.1016/j.dt.2019.04.014. [26] DEWEY J M. Addendum: an interface to provide the physical properties of blast waves generated by propane explosions [J]. Shock Waves, 2020, 30(4): 439–441. DOI: 10.1007/s00193-020-00945-0. [27] DEWEY J M. An interface to provide the physical properties of the blast wave from a free-field TNT explosion [J]. Shock Waves, 2022, 32(4): 383–390. DOI: 10.1007/s00193-022-01076-4. [28] DOBRATZ B M, CRAWFORD P C. LLNL explosives handbook: properties of chemical explosives and explosive simulants: UCRL-52997-Chg. 2 [R]. Livermore: Lawrence Livermore National Laboratory, 1985. [29] SHERKAR P, SHIN J, WHITTAKER A, et al. Influence of charge shape and point of detonation on blast-resistant design [J]. Journal of Structural Engineering, 2016, 142(2): 04015109. DOI: 10.1061/(ASCE)ST.1943-541X.0001371. [30] XIAO W F, ANDRAE M, GEBBEKEN N. Effect of charge shape and initiation configuration of explosive cylinders detonating in free air on blast-resistant design [J]. Journal of Structural Engineering, 2020, 146(8): 04020146. DOI: 10.1061/(ASCE)ST.1943-541X.0002694. [31] BRODE H L. A calculation of the blast wave from a spherical charge of TNT: AD 144302 [R]. US Air Force, 1957. [32] LUTSKY M. The flow behind a spherical detonation in TNT using the Landau-Stanyukovich equation of state for detonation products: NOL-TR 64-40 [R]. White Oak: U. S. Naval Ordnance Laboratory, 1965. [33] 杜红棉, 曹学友, 何志文, 等. 近地爆炸空中和地面冲击波特性分析和验证 [J]. 弹箭与制导学报, 2014, 34(4): 65–68. DOI: 10.3969/j.issn.1637-9728.2014.04.018.DU H M, CAO X Y, HE Z W, et al. Analysisand validation for characteristics of air and ground shock wave near field explosion [J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2014, 34(4): 65–68. DOI: 10.3969/j.issn.1637-9728.2014.04.018. [34] GAJEWSKI T, SIELICKI P W. Experimental study of blast loading behind a building corner [J]. Shock Waves, 2020, 30(4): 385–394. DOI: 10.1007/s00193-020-00936-1. [35] 贾雷明, 王澍霏, 田宙. 爆炸冲击波反射流场的理论计算方法 [J]. 爆炸与冲击, 2019, 39(6): 064201. DOI: 10.11883/bzycj-2018-0167.JIA L M, WANG S F, TIAN Z. A theoretical method for the calculation of flow field behind blast reflected waves [J]. Explosion and Shock Waves, 2019, 39(6): 064201. DOI: 10.11883/bzycj-2018-0167. [36] XIAO W, ANDRAE M, GEBBEKEN N. Development of a new empirical formula for prediction of triple point path [J]. Shock Waves, 2020, 30(6): 677–686. DOI: 10.1007/s00193-020-00968-7. [37] NEEDHAM C E. Blast loads and propagation around and over a building [M]//HANNEMANN K, SEILER F. Shock Waves. Berlin: Springer, 2009. DOI: 10.1007/978-3-540-85181-3. -
计量
- 文章访问数: 222
- HTML全文浏览量: 98
- PDF下载量: 157
- 被引次数: 0