Quasi-one-dimensional numerical study of shock tunnel flows based on cubic equations of state
-
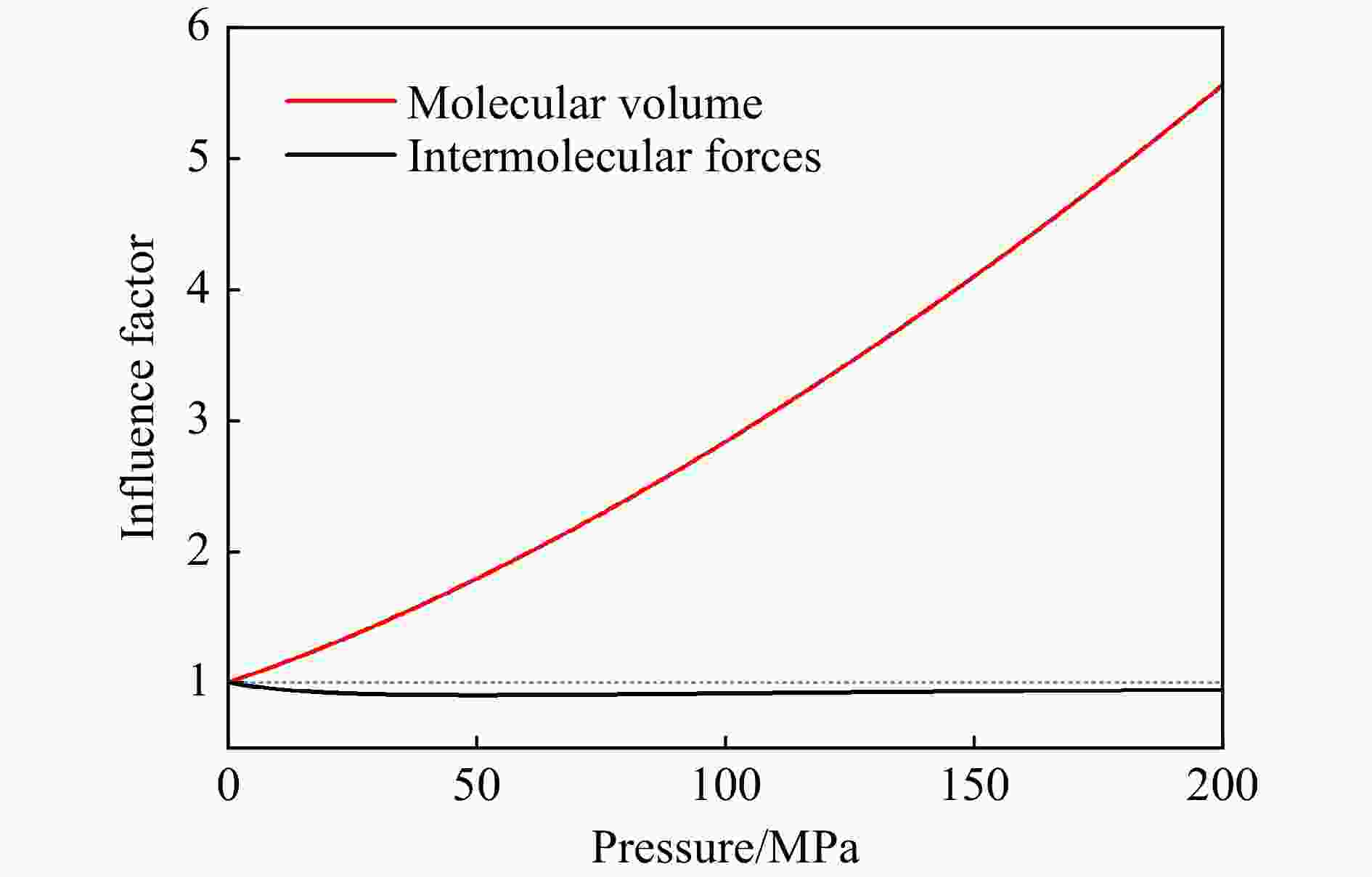
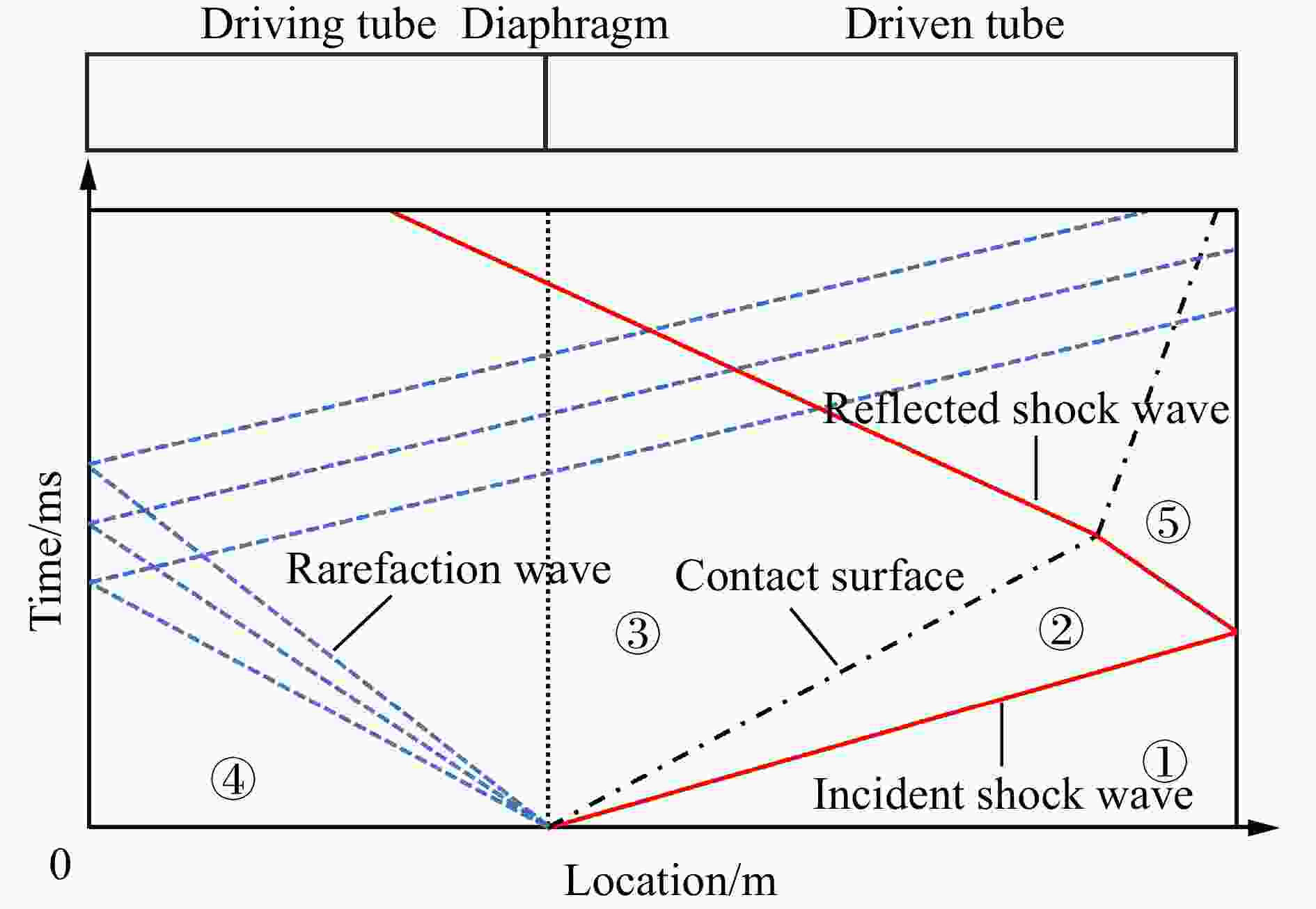
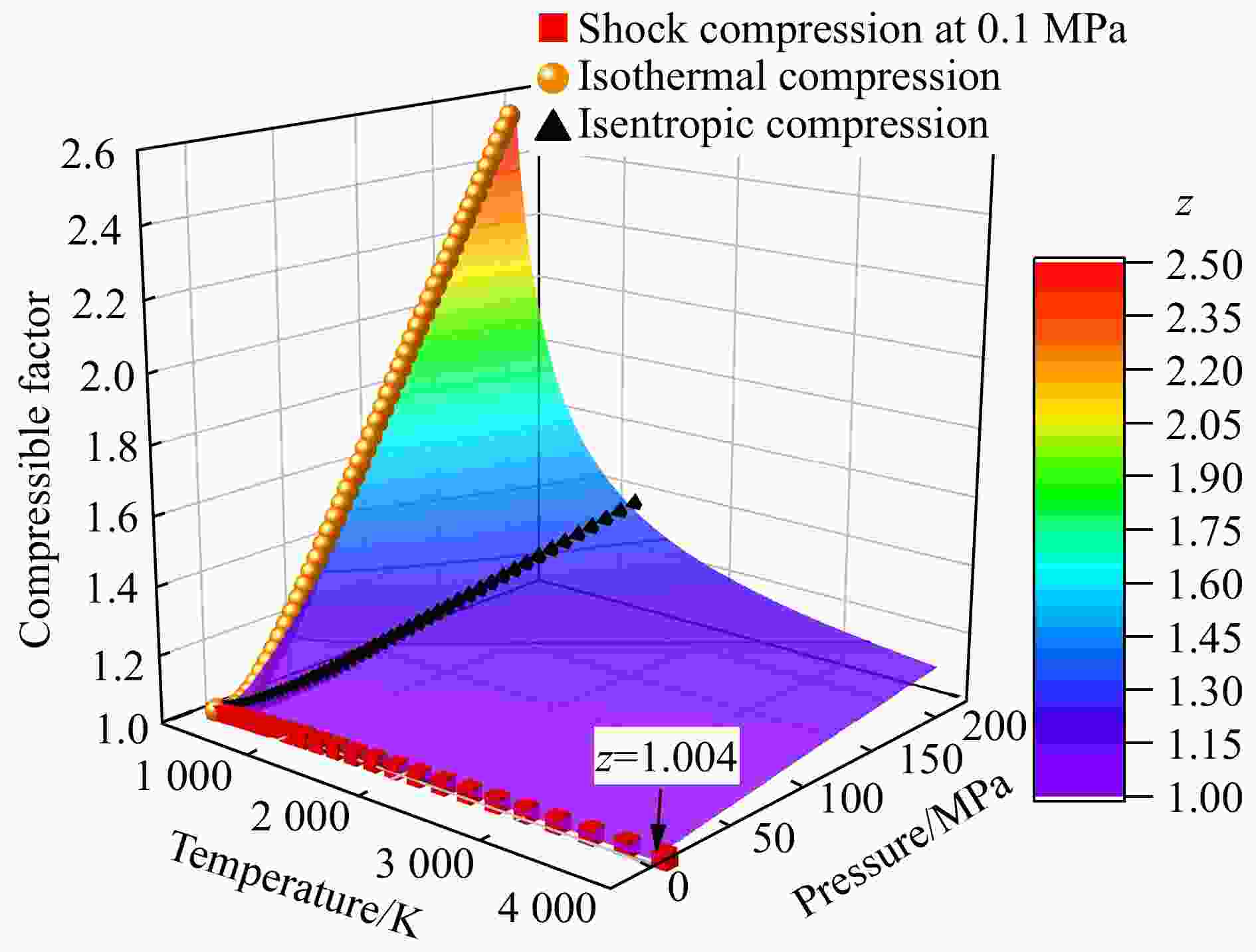
摘要: 采用基于立方型气体状态方程的准一维流动数值模拟方法研究了反射式高焓激波风洞的真实气体流动,重点关注了高压真实气体效应对风洞全场流动时空结构和驻室区气流参数的影响,并以理论分析揭示了高压真实气体效应对激波管内流动的作用机理。研究表明:对于以冷高压气体驱动的激波风洞,使用考虑分子体积和分子间作用力的真实气体状态方程能够更准确地描述气体的状态和风洞内的流动状况。高压真实气体效应主要在冷驱动气体中发生作用,其作用效果主要是使当地声速增大,从而使得入射稀疏波和反射稀疏波的传播速度加快;另一方面,高压气体效应在高温气体效应较显著的被驱动气体中作用微弱,且对激波管产生激波的强度和激波后的流动状态影响甚微。稀疏波的加快传播改变了激波管波系的相干时空关系。提前抵达的稀疏波可在一定情况下侵蚀激波风洞的有效试验时间。对于所测试的激波风洞构型,在150 MPa氢气驱动110 kPa氮气的工况下,高压效应导致的有效试验时间缩短约38%。适当加长驱动段长度和采用高温气体驱动均可有效减弱高压真实气体效应的影响。Abstract: The real gas flows of a reflected high-enthalpy shock tunnel are investigated by quasi-one-dimensional numerical simulation based on cubic equations of state, focusing on the influence of high-pressure real gas effect on the spatio-temporal structure of the full-field flow and the flow parameters in the stagnation zone right before the nozzle throat. In the numerical simulations, the thermochemical non-equilibrium due to high temperature caused by shock waves is considered. By embedding cubic equations of state into gas dynamics relations, theoretical analysis is also performed to find out the mechanism of high-pressure effect on the shock tube flow. It is shown that for shock tunnel flows driven by cold and high-pressure gas, the use of a real gas equation of state that takes into account molecular volume and intermolecular forces can more accurately describe the thermodynamic states of gas and the flow conditions in shock tunnels. The high-pressure real gas effect mainly occurs in the cold driving gas, which increases the local sound speed and hence increases the propagation speed of the incident and reflected rarefaction waves; on the other hand, the high-pressure real gas effect plays a weak role in the driven section where the high-temperature gas effect is significant, while it has little effect on the intensity of the shock wave generated by the shock tube as well as the flow state behind the shock. The increase of rarefaction wave speed changes the intersecting time and space of the wave system, which may alter the order of arrival of the reflected rarefaction wave and the contact surface in the stagnation zone. Under this circumstance, the early arrival of rarefaction wave shortens the effective test time of the shock tunnel. For the tested shock tunnel configuration, the high-pressure real gas effect reduces the effective test time by about 38% under the condition of 150 MPa hydrogen driving 110 kPa nitrogen. Both lengthening of the driver section and using high-temperature driver gas can effectively dissolve the influence of the aforementioned high-pressure effect.
-
表 1 激波风洞运行典型工况
Table 1. Typical operating conditions of the shock tunnel
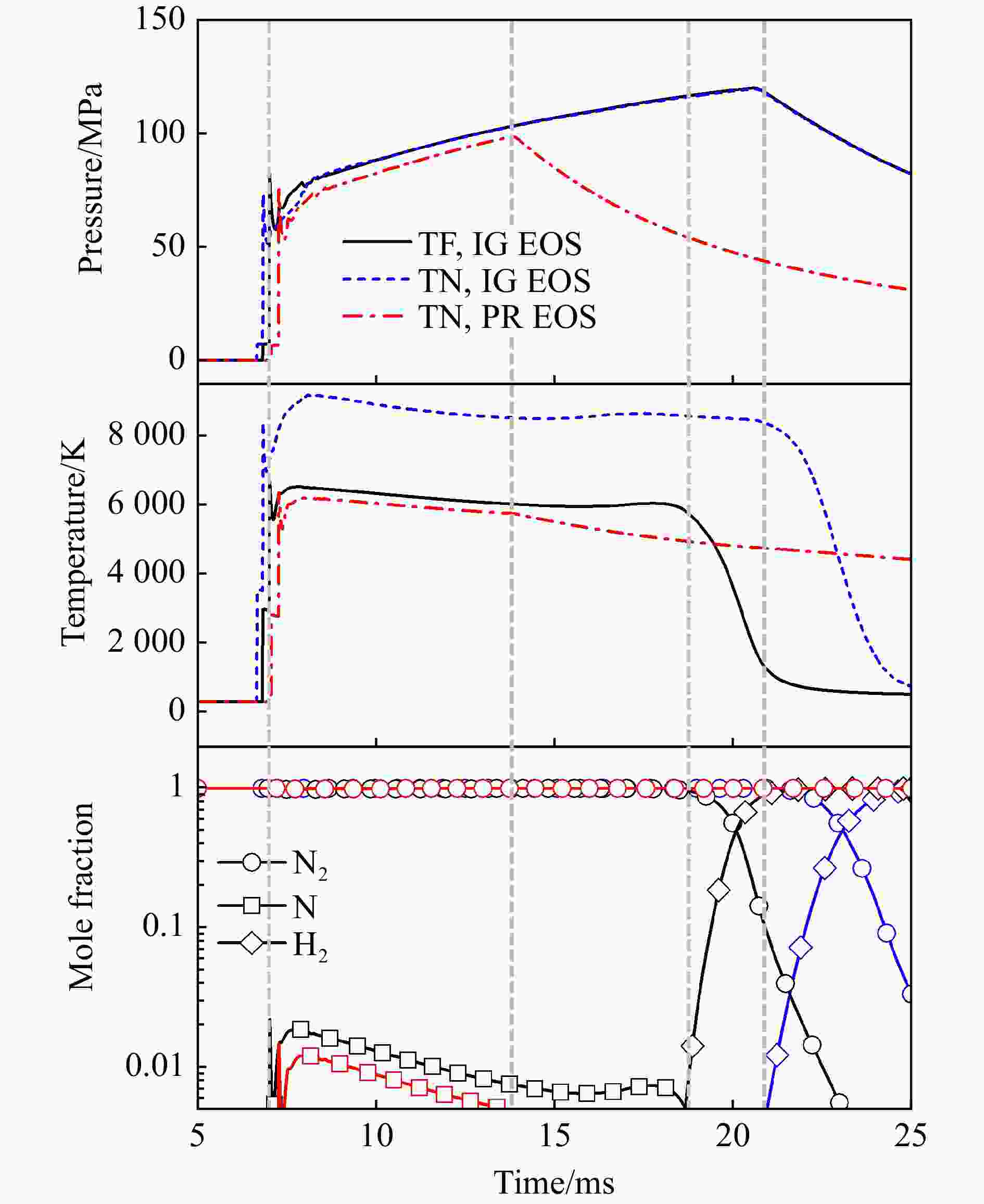
管段 压强/Pa 温度/K 初始组分 长度/m 驱动段 5×107 300 氢气 9 被驱动段 1×105 空气 18 喷管 1 空气 7.5 表 2 激波风洞运行工况
Table 2. Operating conditions of shock tunnel
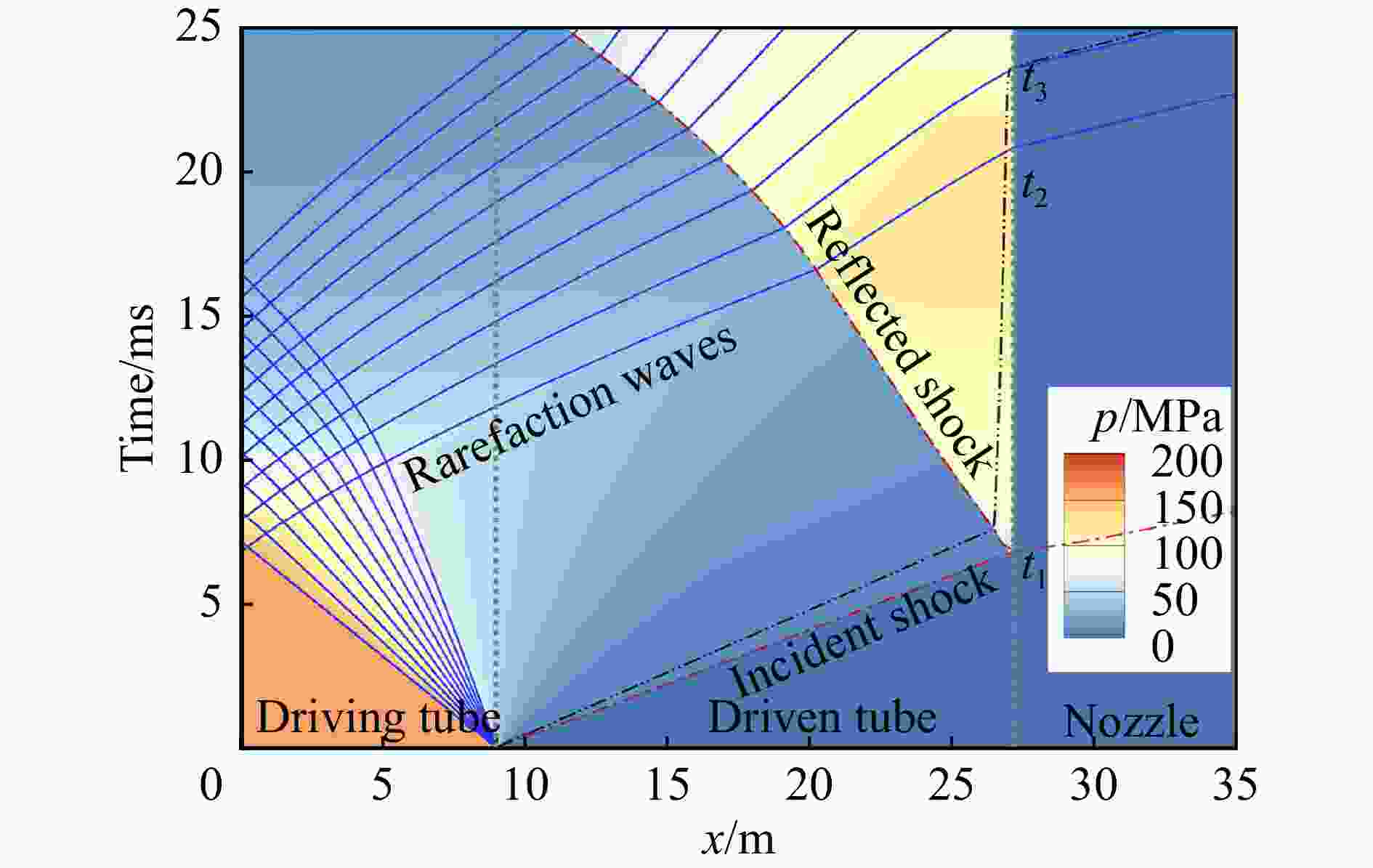
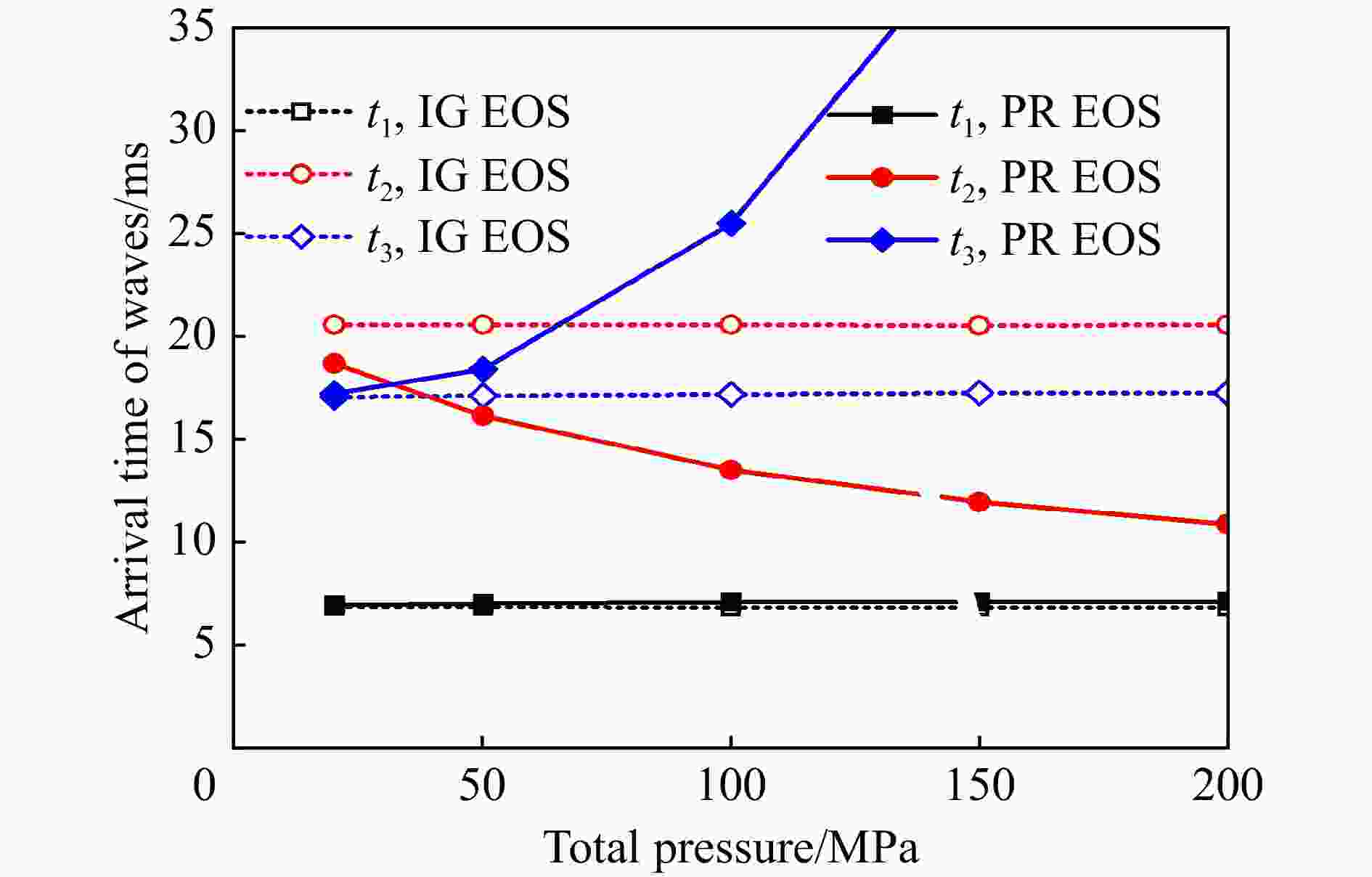
管段 压强/Pa 温度/K 初始组分 长度/m 驱动段 15×107 300 氢气 9.0 被驱动段 11×104 氮气 18.0 喷管 10 氮气 7.5 表 3 各个波系到达驻室入口时刻
Table 3. Arrival time of each wave to stagnation zone
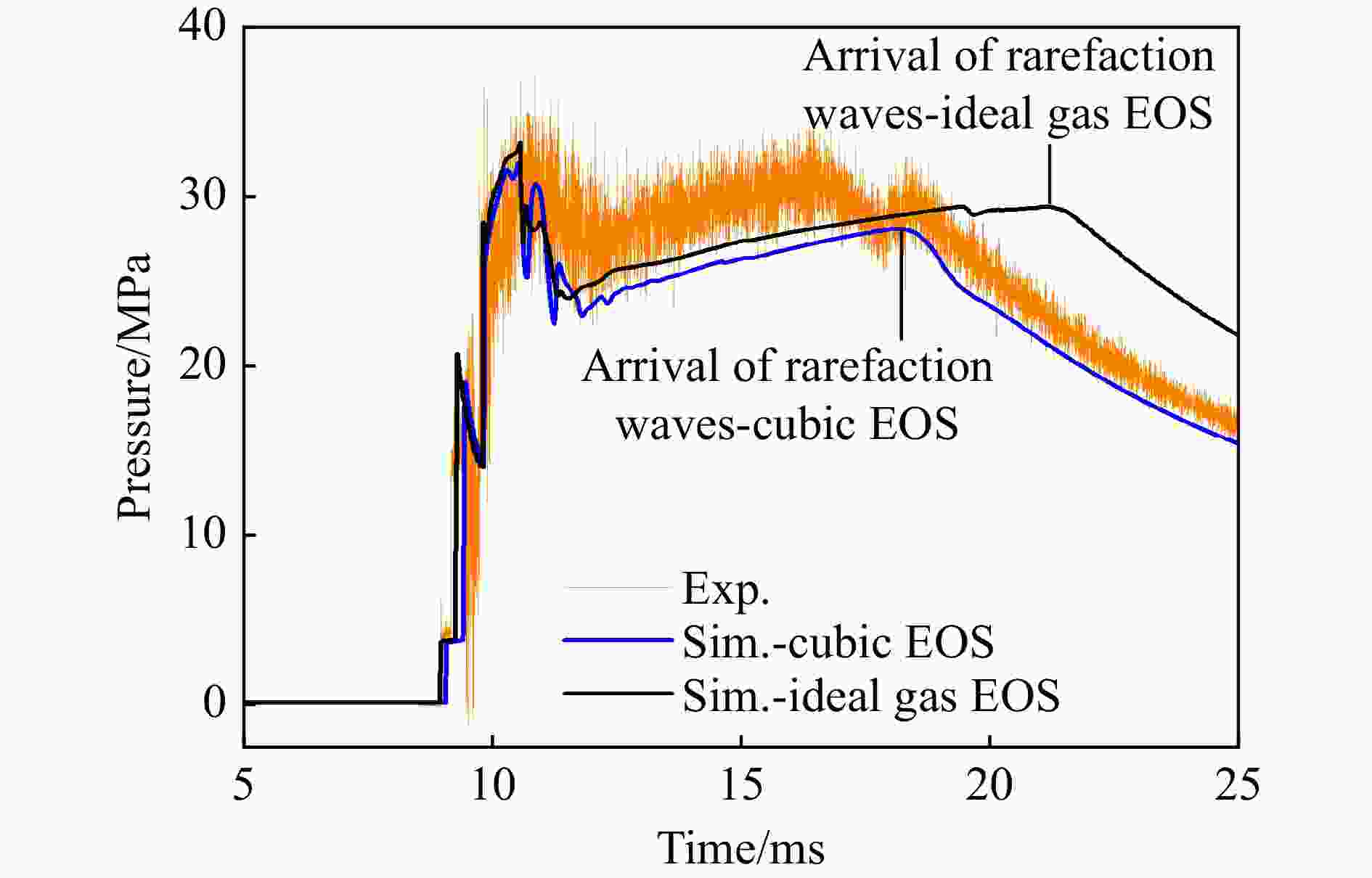
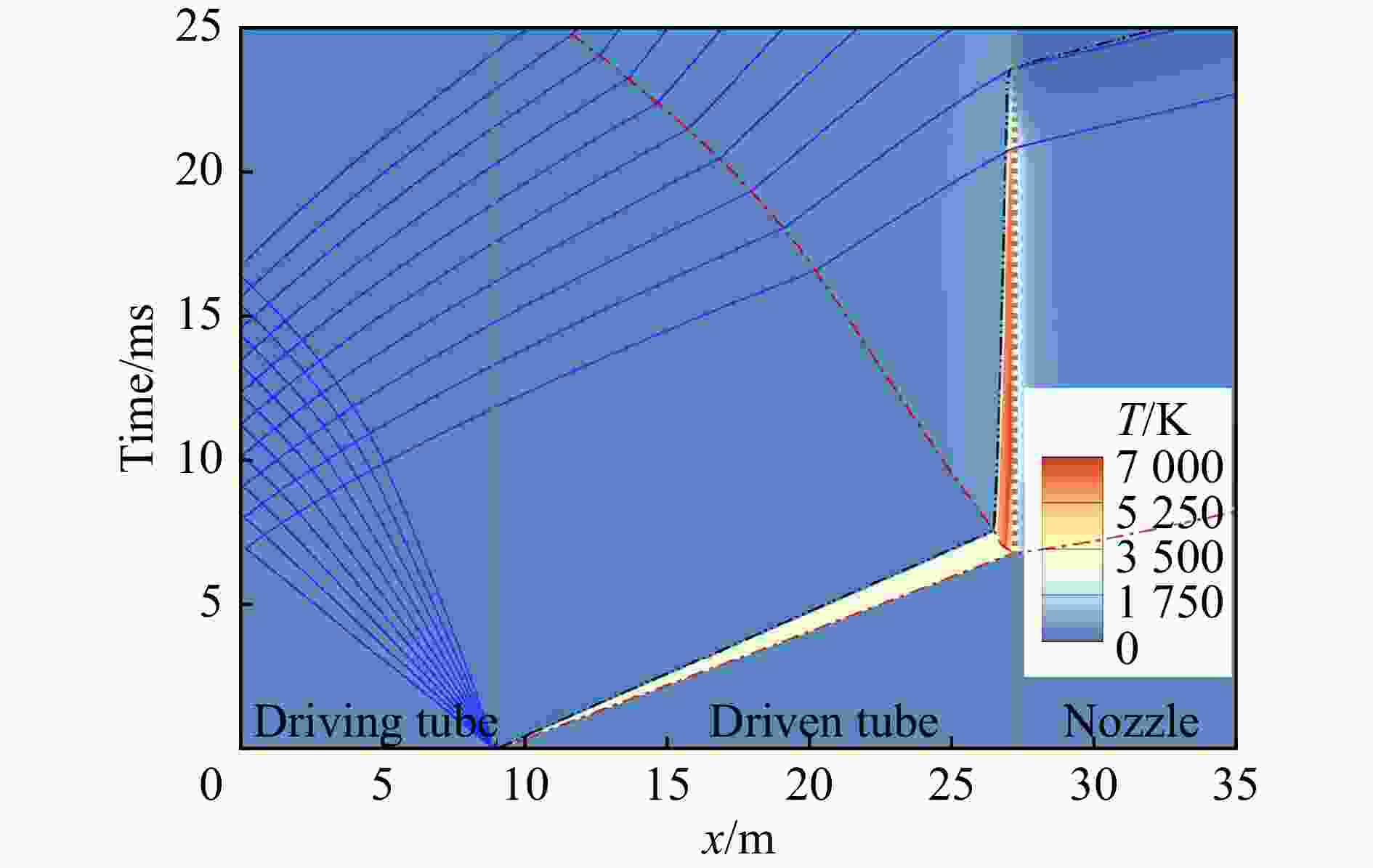
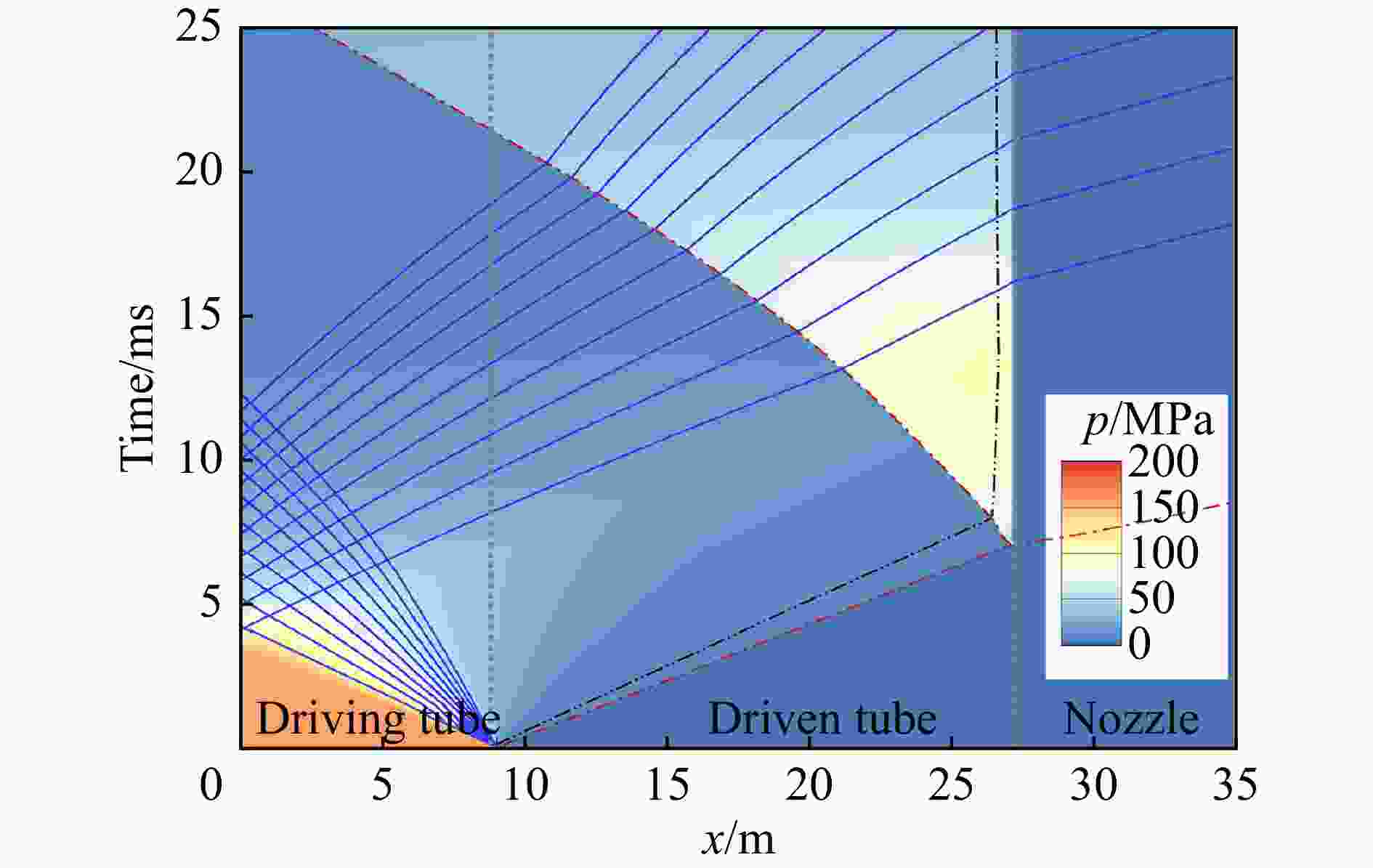
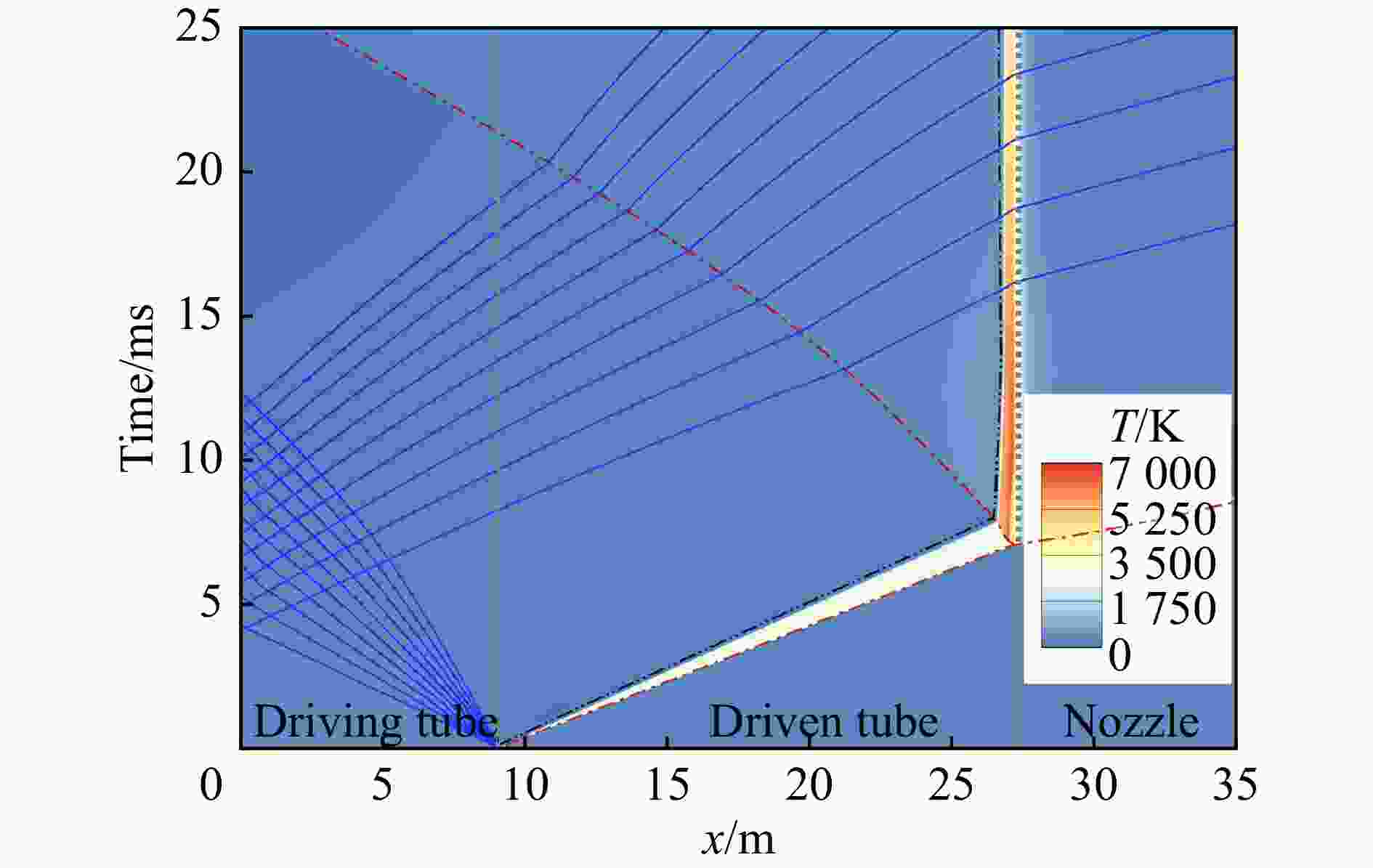
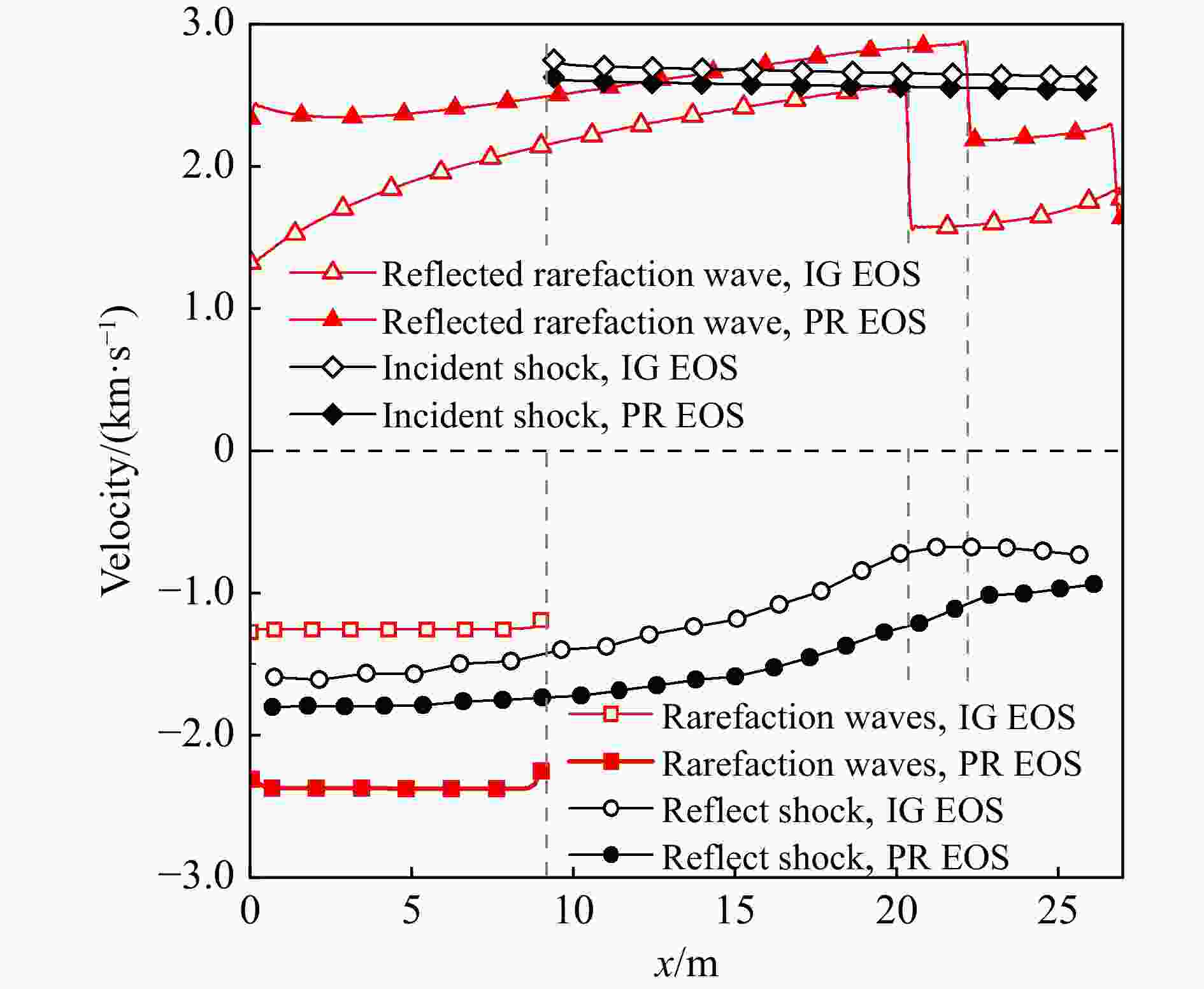
方程 ${t_1}$/ms ${t_2}$/ms ${t_3}$/ms ${t_{{\text{eff}}}}$/ms 理想气体状态方程 6.8 20.6 17.2 10.4 PR状态方程 7.1 13.5 25.5 6.4 表 4 激波风洞试验气流名义总温对应的初始压比和驱动气体氮气摩尔分数
Table 4. Initial pressure ratios and molar fractions of nitrogen in driver gas corresponding to different nominal total temperatures of test flow in the shock tunnel
总温/K 初始压比 氮气摩尔分数/% 2000 176.5 15.0 3000 444.4 9.5 4000 800.0 5.0 5000 1272.7 1.8 6000 1600.0 0 -
[1] ANDERSON J D JR. Hypersonic and high-temperature gas dynamics [M]. 2nd ed. Reston, Virginia, USA: AIAA, 2006: 449–461. DOI: 10.2514/4.861956. [2] VAN DER WAALS J D. On the continuity of the gaseous and liquid state [D]. Leiden, Holland: University of Leiden, 1873. [3] JACOBS P A. Quasi-one-dimensional modeling of a free-piston shock tunnel [J]. AIAA Journal, 1994, 32(1): 137–145. DOI: 10.2514/3.11961. [4] BOYCE R R, TAKAHASHI M, STALKER R J. Mass spectrometric measurements of driver gas arrival in the T4 free-piston shock-tunnel [J]. Shock Waves, 2005, 14(5/6): 371–378. DOI: 10.1007/s00193-005-0276-3. [5] HANNEMANN K. High enthalpy flows in the HEG shock tunnel: experiment and numerical rebuilding [C]//41st Aerospace Sciences Meeting and Exhibit. Reno: AIAA, 2003: 978. DOI: 10.2514/6.2003-978. [6] JOHNSTON I, WEILAND M, SCHRAMM J, et al. Aerothermodynamics of the ARD-Postflight numerics and shock-tunnel experiments [C]//40th AIAA Aerospace Sciences Meeting & Exhibit. Reno: AIAA, 2002: 407. DOI: 10.2514/6.2002-407. [7] HOLDEN M, WADHAMS T, MACLEAN M, et al. Experimental studies in LENS I and X to evaluate real gas effects on hypevelocity vehicle performance [C]//45th AIAA Aerospace Sciences Meeting and Exhibit. Reno: AIAA, 2007: 204. DOI: 10.2514/6.2007-204. [8] 卢洪波, 陈星, 曾宪政, 等. FD-21风洞 Ma=10高超声速推进试验技术探索 [J]. 气体物理, 2022, 7(2): 1–12. DOI: 10.19527/j.cnki.2096-1642.0926.LU H B, CHEN X, ZENG X Z, et al. Exploration of experimental techniques on Ma=10 scramjets in FD-21 high enthalpy shock tunnel [J]. Physics of Gases, 2022, 7(2): 1–12. DOI: 10.19527/j.cnki.2096-1642.0926. [9] LLOBET J R, YAMADA G, TONIATO P. Quasi-0D-model mapping of reflected shock tunnel operating conditions [J]. AIAA Journal, 2020, 58(4): 1668–1680. DOI: 10.2514/1.J058660. [10] LYNCH K P, GRASSER T, FARIAS P, et al. Design and characterization of the Sandia free-piston reflected shock tunnel [C]//AIAA SCITECH 2022 Forum. San Diego: AIAA, 2022: 0968. DOI: 10.2514/6.2022-0968. [11] GORDON S, MCBRIDE B J. Computer program for calculation of complex chemical equilibrium compositions and applications. Part 1: analysis: NASA RP-1311 [R]. Cleveland, Ohio, USA: NASA, 1996. [12] LUO K, WANG Q, LI J W, et al. Numerical modeling of a high-enthalpy shock tunnel driven by gaseous detonation [J]. Aerospace Science and Technology, 2020, 104: 105958. DOI: 10.1016/j.ast.2020.105958. [13] MACLEAN M, WADHAMS T, HOLDEN M, et al. Investigation of blunt bodies with CO2 test gas including catalytic effects [C]//38th AIAA Thermophysics Conference. Toronto: AIAA, 2005: 4693. DOI: 10.2514/6.2005-4693. [14] MACLEAN M, DUFRENE A, WADHAMS T, et al. Numerical and experimental characterization of high enthalpy flow in an expansion tunnel facility [C]//48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Orlando: AIAA, 2010: 1562. DOI: 10.2514/6.2010-1562. [15] CANDLER G. Hypersonic nozzle analysis using an excluded volume equation of state [C]//38th AIAA Thermophysics Conference. Toronto: AIAA, 2005: 5202. DOI: 10.2514/6.2005-5202. [16] SIRIGNANO W A. Compressible flow at high pressure with linear equation of state [J]. Journal of Fluid Mechanics, 2018, 843: 244–292. DOI: 10.1017/jfm.2018.166. [17] 王刚, 马晓伟, 江涛, 等. 前向空腔的弓形激波特性研究 [J]. 宇航学报, 2016, 37(8): 901–907. DOI: 10.3873/j.issn.1000-1328.2016.08.002.WANG G, MA X W, JIANG T, et al. Characteristics of bow shock for a forward-facing cavity [J]. Journal of Astronautics, 2016, 37(8): 901–907. DOI: 10.3873/j.issn.1000-1328.2016.08.002. [18] GROTH C P T, GOTTLIEB J J. Numerical study of two-stage light-gas hypervelocity projectile launchers: UTIAS Report 372 [R]. Toronto: University of Toronto Intsitute for Aerospace Studies, 1988. [19] WILKE C R. A viscosity equation for gas mixtures [J]. The Journal of Chemical Physics, 1950, 18(4): 517–519. DOI: 10.1063/1.1747673. [20] PARK C. Assessment of two-temperature kinetic model for ionizing air [J]. Journal of Thermophysics and Heat Transfer, 1989, 3(3): 233–244. DOI: 10.2514/3.28771. [21] MILLIKAN R C, WHITE D R. Systematics of vibrational relaxation [J]. The Journal of Chemical Physics, 1963, 39(12): 3209–3213. DOI: 10.1063/1.1734182. [22] GUPTA R N, YOS J M, THOMPSON R A. A review of reaction rates and thermodynamic and transport properties for the 11-species air model for chemical and thermal nonequilibrium calculations to 30000 K: NASA TM-101528 [R]. Hampton: NASA, 1990. [23] DUNN M G, KANG S. Theoretical and experimental studies of reentry plasmas: NASA CR-2232 [R]. Buffalo, New York, USA: NASA, 1973. [24] TORO E F, SPRUCE M, SPEARES W. Restoration of the contact surface in the HLL-Riemann solver [J]. Shock Waves, 1994, 4(1): 25–34. DOI: 10.1007/bf01414629. [25] 侯自豪, 朱雨建, 薄靖龙, 等. 真空管道列车准一维气动特性 [J]. 机械工程学报, 2022, 58(6): 119–129. DOI: 10.3901/JME.2022.06.119.HOU Z H, ZHU Y J, BO J L, et al. Quasi-one-dimensional aerodynamic characteristics of tube train [J]. Journal of Mechanical Engineering, 2022, 58(6): 119–129. DOI: 10.3901/JME.2022.06.119. [26] HOU Z H, ZHU Y J, BO J L, et al. A quasi-one-dimensional study on global characteristics of tube train flows [J]. Physics of Fluids, 2022, 34(2): 026104. DOI: 10.1063/5.0080544. [27] YANG J T, ZHU Y J, YANG J M. Self-ignition induced by cylindrically imploding shock adapting to a convergent channel [J]. Physics of Fluids, 2017, 29(3): 031702. DOI: 10.1063/1.4979135. [28] 中国空气动力研究与发展中心超高速空气动力研究所, 中国科学技术大学. 超高压激波类设备热化学非平衡准一维计算软件. V1.0: 2022SR0066696 [P]. 2022-01-11. [29] PENG D Y, ROBINSON D B. A new two-constant equation of state [J]. Industrial and Engineering Chemistry Fundamentals, 1976, 15(1): 59–64. DOI: 10.1021/i160057a011. [30] LOPEZ-ECHEVERRY J S, REIF-ACHERMAN S, ARAUJO-LOPEZ E. Peng-Robinson equation of state: 40 years through cubics [J]. Fluid Phase Equilibria, 2017, 447: 39–71. DOI: 10.1016/j.fluid.2017.05.007. [31] SOAVE G. Equilibrium constants from a modified Redlich-Kwong equation of state [J]. Chemical Engineering Science, 1972, 27(6): 1197–1203. DOI: 10.1016/0009-2509(72)80096-4. [32] ZUDKEVITCH D, JOFFE J. Correlation and prediction of vapor-liquid equilibria with the Redlich-Kwong equation of state [J]. AIChE Journal, 1970, 16(1): 112–119. DOI: 10.1002/aic.690160122. [33] POLING B E, PRAUSNITZ J M, O’CONNELL J P. Properties of gases and liquids [M]. 5th ed. New York: McGraw-Hill Education, 2001: 151-155. [34] KAY W B. Gases and vapors at high temperature and pressure: density of hydrocarbon [J]. Industrial and Engineering Chemistry, 1936, 28(9): 1014–1019. DOI: 10.1021/ie50321a008. [35] LINSTROM P J, MALLARD W G. The NIST Chemistry WebBook: a chemical data resource on the internet [J]. Journal of Chemical and Engineering Data, 2001, 46(5): 1059–1063. DOI: 10.1021/je000236i. -







 下载:
下载: