Robust explicit computational strategies based on penalty method for large-deformation impact problems
-
摘要: 为了提高基于罚函数法的显式有限元对大变形接触-碰撞问题仿真的精确性和健壮性，基于前增量位移中心差分方法，发展了一种新的大变形接触非侵入算法。将动力方程求解步分解为不考虑接触的预估步和考虑接触的修正步，在当前时刻，采用罚函数法施加接触惩罚力，使其满足非侵入条件，从而提高显式接触计算的精确性；在仅能获得下一时刻位移的情况下，为了精确计算下一时刻的大变形内力，基于任意参考构型大变形理论，将动力学方程内力项映射到已知的参考构型求解，避免使用相关物理量的中间构型近似值，从而降低由大变形计算引入的数值误差。更严格的几何非线性算法以及接触算法可有效抑制实体间的非物理穿透和大变形碰撞过程中的单元畸变，提高计算程序的健壮性。对典型碰撞及侵彻算例进行仿真，并与商业软件的结果进行对比，验证了所发展的大变形接触-碰撞显式算法的正确性，并证明了在高速大变形碰撞仿真方面，当前接触-碰撞显式算法比基于蛙跳格式中心差分和罚函数法的经典接触-碰撞算法更加健壮。Abstract: To improve the accuracy and robustness of the explicit finite element algorithm based on penalty method for simulating large deformation impact-contact problem, a new large-deformation non-penetration contact algorithm based on forward incremental displacement central difference (FIDCD) is developed. On the one hand, according to FIDCD, the solving step of the dynamic equation is decomposed into an estimated step without considering contact and a correction step considering contact constraint. At the current moment, a contact force is applied through the penalty method to make the deformation of entities satisfy the non-penetration condition. The contact force is calculated by a soft constraint penalty stiffness, which helps to maintain stability of contact localization. It refines the numerical accuracy of the explicit contact computation. On the other hand, to accurately calculate the large-deformation internal force of the next moment while only obtaining the displacement, the internal force term of the dynamic equation is mapped to a known configuration for solution based on the arbitrary reference configurations (ARC) theory. It avoids using the values of variables at intermediate configuration to approximate them, thereby improving the numerical accuracy of the large deformation computation. More rigorous contact algorithms and geometric nonlinear solution strategy can effectively suppress mesh distortion and non-physical penetration between entities during large-deformation impact simulation. This thus improves the robustness of the new explicit algorithm. Finally, the computational program written according to the new developed algorithm is applied to simulate several impact and penetration examples with different impact velocities. By comparing the simulation results with those obtained from commercial software, the correctness of the developed algorithm and computational program is verified. At the same time, it can also be proven that the algorithm proposed is more robust in simulating high-speed and large-deformation impact problems than the classical explicit impact-contact algorithm based on the frog jump center difference scheme combining with penalty method.
-
图 3 v0=350 m/s、t=100 μs时撞击杆中心截面等效塑性应变分布
Figure 3. Equivalent plastic strain distribution at the central section of the impact bar when v0=350 m/s, t=100 μs
图 4 v0=350 m/s时撞击杆上不同质点的速度历史与撞击杆动能演化曲线
Figure 4. Velocity histories of several material points and kinetic energy evolution curves of the impact bar when v0=350 m/s
图 5 v0=700 m/s工况下不同时刻撞击杆与靶体接触局部变形
Figure 5. Local deformation of the impact bar and the target at different times when v0=700 m/s
图 7 偏撞情况下不同时刻两杆的变形状态
Figure 7. Deformation configurations of two bars at different times under offset impact
图 8 偏撞情况下采用本文算法预测的28 μs时刻等效塑性应变分布
Figure 8. Equivalent plastic strain distribution at 28 μs under offset impact predicted by the present method
图 9 瞬态冲击格栅结构的初始状态
Figure 9. Initial configuration of transient impact grille structure problem
表 1 撞击杆与靶体材料参数
Table 1. Material parameters of impact bar and target
部件 ρ0/(kg·m−3) E/GPa ν σy/MPa 撞击杆 4400 256 0.2 860 靶体 7800 390 0.3 620 
下载: 导出CSV
表 2 正撞情况下不同时刻两杆的变形状态
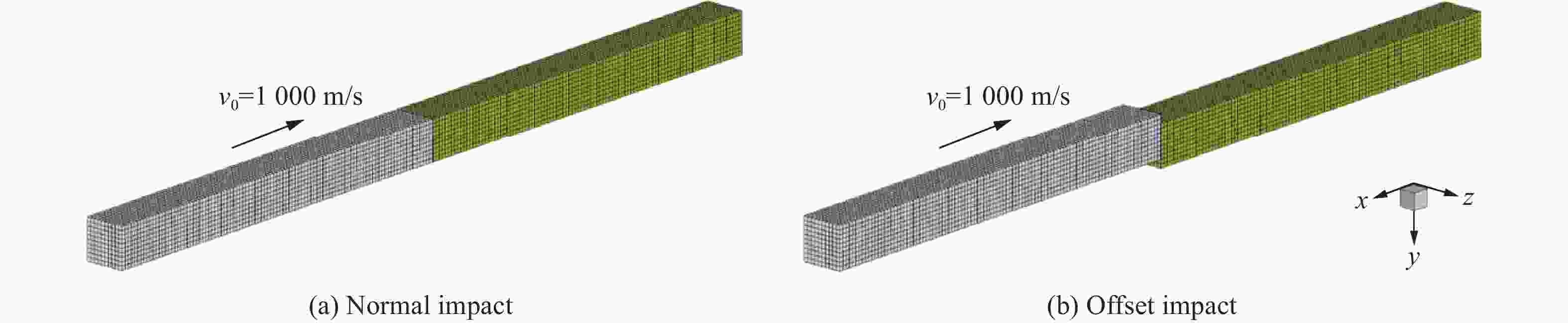
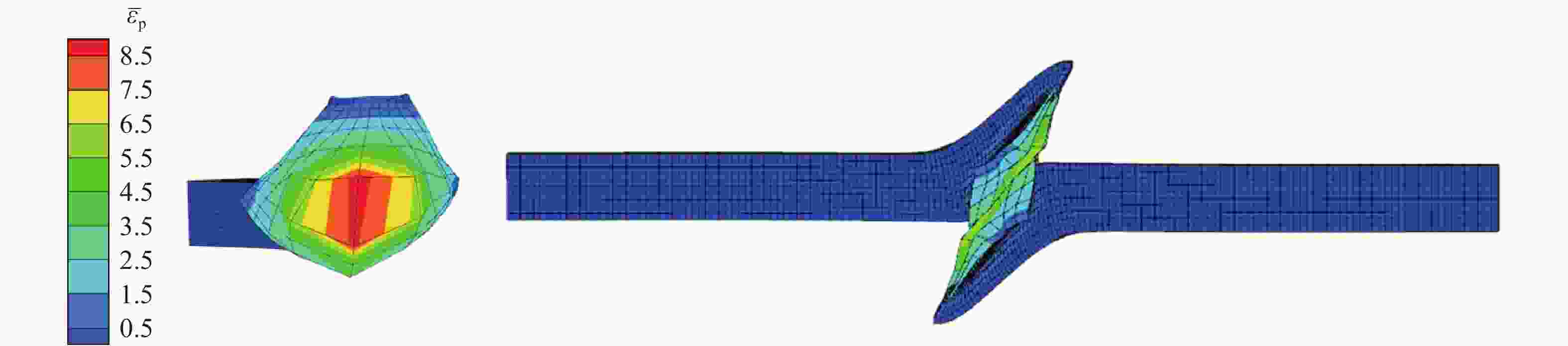
Table 2. Deformation configurations of two bars at different times under normal impact
时间/μs 变形状态 本文算法 LS-DYNA （SOFSCL取1.0，
SFS和SFM取1.0）LS-DYNA（SOFSCL取1.0，
SFS和SFM取10.0）10 
20 
30 
110 
下载: 导出CSV
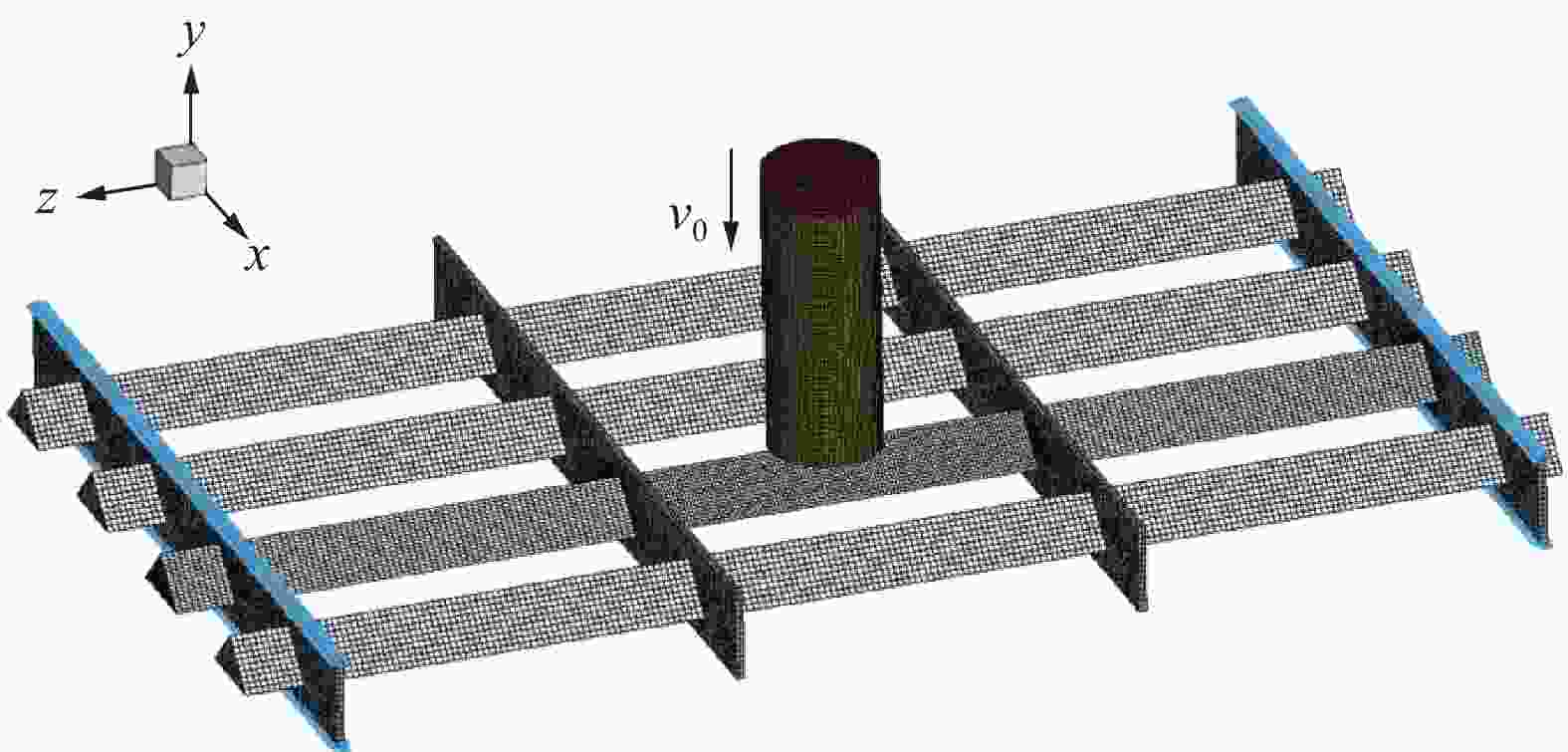
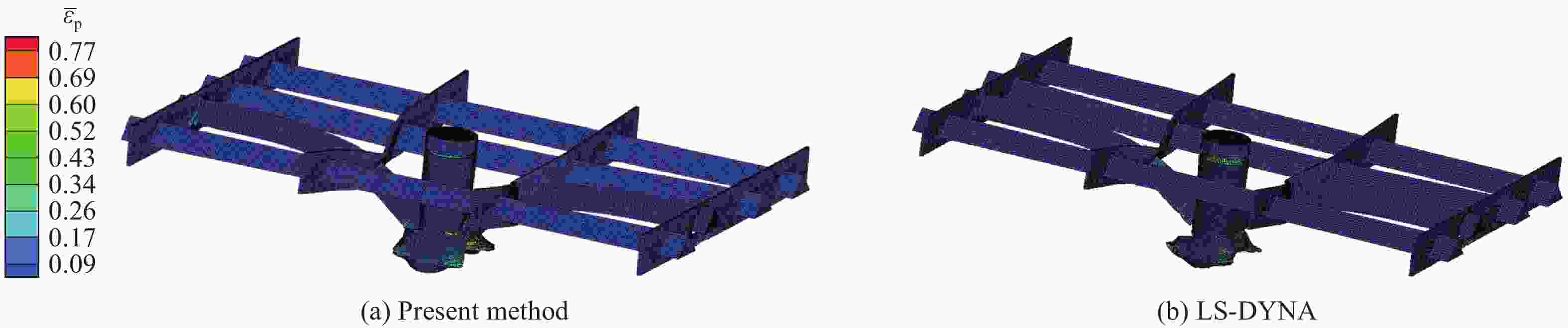
表 4 弹体外壳与格栅结构失效的材料参数
Table 4. Material parameters for failure description of projectile shell and grille structure
部件 D1 D2 D3 D4 D5 弹体外壳 −0.02 0.4 −1.96 0 0 格栅结构 −0.1 0.5 − 0.6141 0 0
下载: 导出CSV
表 3 弹体外壳与格栅结构变形的材料参数
Table 3. Material parameters for deformation description of projectile shell and grille structure
部件 ρ0/(kg·m−3) E/GPa ν A/MPa B/MPa C n $ {\dot \varepsilon_{{0}}} $/s−1 弹体外壳 7800 210 0.3 1453 810 0.003 0.479 2×10−6 格栅结构 7800 210 0.3 706 648 0.013 0.58 2×10−6
下载: 导出CSV
表 5 装药的材料参数
Table 5. Material parameters of charge
ρ0/(kg·m−3) E/GPa ν σy/MPa εf 1460 60 0.3 30 0.8
下载: 导出CSV
-
[1] BELYTSCHKO T, LIU W K, MORAN B, et al. Nonlinear finite elements for continua and structures [M]. 2nd ed. Chichester: John Wiley & Sons Inc. , 2014: 330–335. [2] 钟阳, 钟志华, 李光耀, 等. 机械系统接触碰撞界面显式计算的算法综述 [J]. 机械工程学报, 2011, 47(13): 44–58. DOI: 10.3901/JME.2011.13.044.ZHONG Y, ZHONG Z H, LI G Y, et al. Review on Contact algorithms calculating the contact-impact interface in mechanical system with explicit FEM [J]. Journal of Mechanical Engineering, 2011, 47(13): 44–58. DOI: 10.3901/JME.2011.13.044. [3] ZHOU X, SHA D, TAMMA K K. A robust consistent configuration framework and formulation for 3D finite strain dynamic impact problems [J]. Computer Methods in Applied Mechanics and Engineering, 2008, 197(51/52): 4571–4590. DOI: 10.1016/j.cma.2008.06.001. [4] 张雄, 王天舒, 刘岩. 计算动力学 [M]. 2版. 北京: 清华大学出版社, 2015: 249–265.ZHANG X, WANG T S, LIU Y. Computational dynamics [M]. 2nd ed. Beijing: Tsinghua University Press, 2015: 249–265. [5] HALLQUIST J O. LS-DYNA theory manual [M]. Livermore: Livermore Software Technology Corporation, 2006: 523–556. [6] 陈成军, 陈小伟, 柳明. 接触-碰撞算法研究进展 [J]. 计算力学学报, 2018, 35(3): 261–274. DOI: 10.7511/jslx20160817002.CHEN C J, CHEN X W, LIU M. Review of research progress in contact-impact algorithms [J]. Chinese Journal of Computational Mechanics, 2018, 35(3): 261–274. DOI: 10.7511/jslx20160817002. [7] BOURAGO N G, KUKUDZHANOV V N. A review of contact algorithms [J]. Mechanics of solids, 2005(1): 45–87. [8] Abaqus. Analysis user’s manual, version 6.14 [M]. Providence: Dassault Systemes Simulia Corporation, 2014: 151–155. [9] ZHONG Z H. Finite element procedures for contact-impact problems [M]. New York: Oxford University Press, 1993: 233–251. [10] WANG F J, WANG L P, CHENG J G, et al. Contact force algorithm in explicit transient analysis using finite-element method [J]. Finite Elements in Analysis and Design, 2007, 43(6/7): 580–587. DOI: 10.1016/j.finel.2006.12.010. [11] SHA D, TAMMA K K, LI M. Robust explicit computational developments and solution strategies for impact problems involving friction [J]. International Journal for Numerical Methods in Engineering, 1996, 39(5): 721–739. DOI: 10.1002/(SICI)1097-0207(19960315)39:5<721::AID-NME865>3.0.CO;2-J. [12] KOLMAN R, KOPAČKA J, GONZÁLEZ J A, et al. Bi-penalty stabilized technique with predictor-corrector time scheme for contact-impact problems of elastic bars [J]. Mathematics and Computers in Simulation, 2021, 189: 305–324. DOI: 10.1016/j.matcom.2021.03.023. [13] KOPAČKA J, TKACHUK A, GABRIEL D, et al. On stability and reflection-transmission analysis of the bipenalty method in contact-impact problems: a one-dimensional, homogeneous case study [J]. International Journal for Numerical Methods in Engineering, 2018, 113(10): 1607–1629. DOI: 10.1002/nme.5712. [14] SEWERIN F, PAPADOPOULOS P. On the finite element solution of frictionless contact problems using an exact penalty approach [J]. Computer Methods in Applied Mechanics and Engineering, 2020, 368: 113108. DOI: 10.1016/j.cma.2020.113108. [15] MOHERDAUI T F, NETO A G, WRIGGERS P. A second-order penalty-based node-to-segment contact using the virtual element method [J]. Finite Elements in Analysis and Design, 2024, 237: 104183. DOI: 10.1016/j.finel.2024.104183. [16] 王福军. 冲击接触问题有限元法并行计算及其工程应用 [D]. 北京: 清华大学, 2000: 72–82.WANG F J. Parallel computation of contact-impact problems with FEM and its engineering application [D]. Beijing: Tsinghua University, 2000: 72–82. [17] ZHOU X, SHA D, TAMMA K K. On a new concept and foundations of an arbitrary reference configuration (ARC) theory and formulation for computational finite deformation applications—Part Ⅰ: elasticity [J]. International Journal for Computational Methods in Engineering Science and Mechanics, 2006, 7(5): 331–351. DOI: 10.1080/15502280600790264. [18] ZHOU X, SHA D, TAMMA K K. On a new concept and foundations of an arbitrary reference configuration (ARC) theory and formulation for computational finite deformation applications—Part Ⅱ: elasto-plasticity [J]. International Journal for Computational Methods in Engineering Science and Mechanics, 2006, 7(5): 353–367. DOI: 10.1080/15502280600790314. [19] ZHOU X M, SHA D S, TAMMA K K, et al. A consistent configuration formulation involving continuum damage mechanics based Lagrangian hydrodynamic computational framework for 3D high- and hypervelocity impact/damage/penetration analysis [C]//47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Newport, USA: AIAA, 2006. DOI: 10.2514/6.2006-1758. [20] SUN D W, LIU C, HU H Y. Dynamic computation of 2D segment-to-segment frictional contact for a flexible multibody system subject to large deformations [J]. Mechanism and Machine Theory, 2021, 158: 104197. DOI: 10.1016/j.mechmachtheory.2020.104197. [21] SUN D W, LIU C, HU H Y. Dynamic computation of 2D segment-to-segment frictionless contact for a flexible multibody system subject to large deformation [J]. Mechanism and Machine Theory, 2019, 140: 350–376. DOI: 10.1016/j.mechmachtheory.2019.06.011. [22] SERROUKH H K, MABSSOUT M, HERREROS M I. Updated Lagrangian Taylor-SPH method for large deformation in dynamic problems [J]. Applied Mathematical Modelling, 2020, 80: 238–256. DOI: 10.1016/j.apm.2019.11.046. [23] ZHENG X C, SEAID M, PISANÒ F, et al. A material point/finite volume method for coupled shallow water flows and large dynamic deformations in seabeds [J]. Computers and Geotechnics, 2023, 162: 105673. DOI: 10.1016/j.compgeo.2023.105673. [24] RÖTHLIN M, KLIPPEL H, WEGENER K. Meshless methods for large deformation elastodynamics [EB/OL]. arXiv: 1807.01117. (2018-07-05)[2024-03-18]. https://doi.org/ 10.48550/arXiv.1807.01117. DOI: 10.48550/arXiv.1807.01117. [25] WRIGGERS P. Computational contact mechanics [M]. 2nd ed. Berlin: Springer, 2006: 11–30. DOI: 10.1007/978-3-540-32609-0. [26] JOHNSON G R, COOK W H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures [J]. Engineering Fracture Mechanics, 1985, 21(1): 31–48. DOI: 10.1016/0013-7944(85)90052-9. [27] HEINSTEIN M W, MELLO F J, ATTAWAY S W, et al. Contact-impact modeling in explicit transient dynamics [J]. Computer Methods in Applied Mechanics and Engineering, 2000, 187(3/4): 621–640. DOI: 10.1016/S0045-7825(99)00342-4. [28] Livermore Software Technology Corporation. LS-DYNA® keyword user’s manual, volume Ⅰ [M]. Livermore: Livermore Software Technology Corporation, 2006: 1407–1170. [29] NOUR-OMID B, WRIGGERS P. A note on the optimum choice for penalty parameters [J]. Communications in Applied Numerical Methods, 1987, 3(6): 581–585. DOI: 10.1002/cnm.1630030620. -
计量
- 文章访问数: 149
- HTML全文浏览量: 55
- PDF下载量: 30
- 被引次数: 0