Damage characteristics of foamed aluminum/fiber sandwich structure under the combined loading of near-field blast shock wave and fragments
-
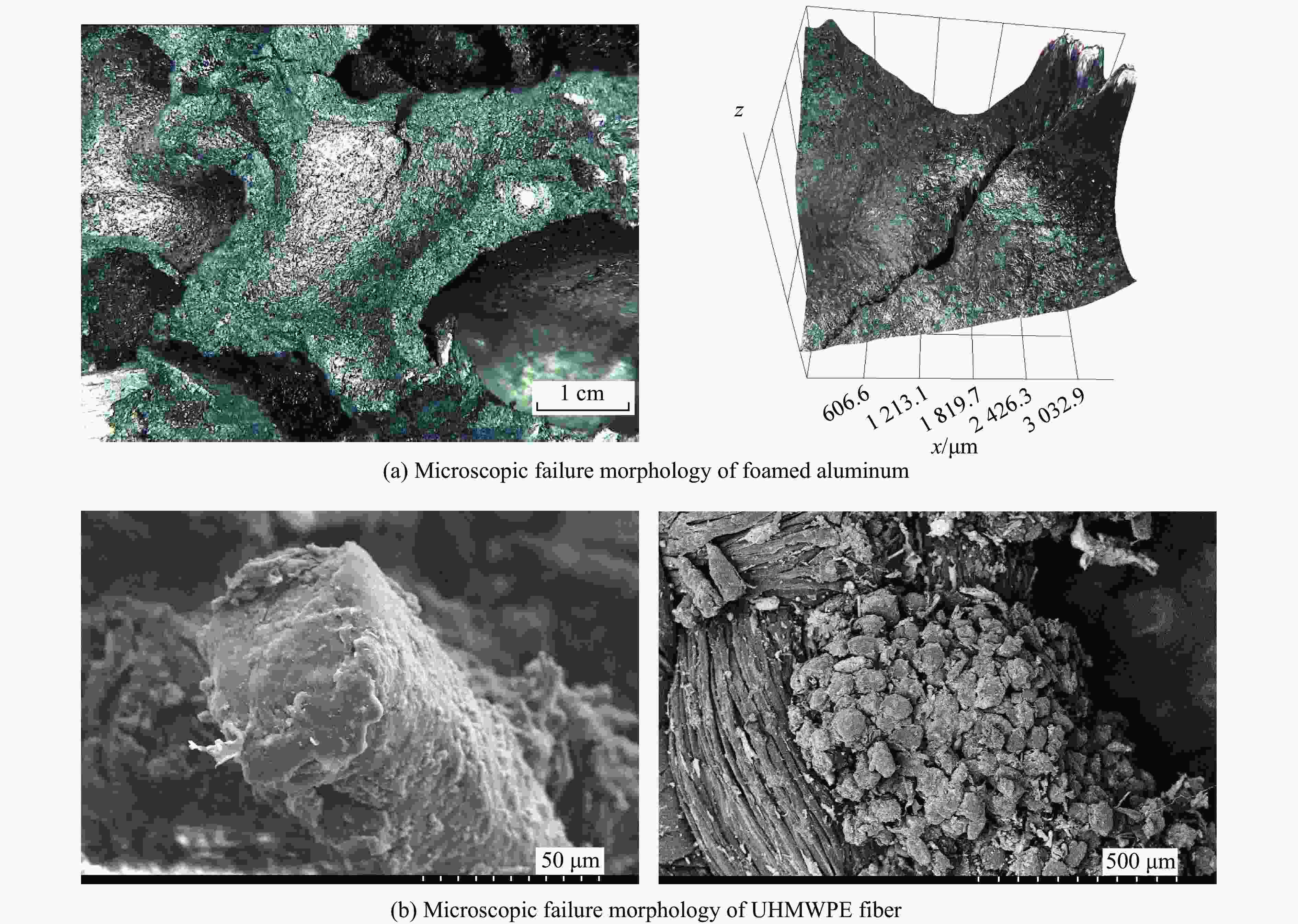
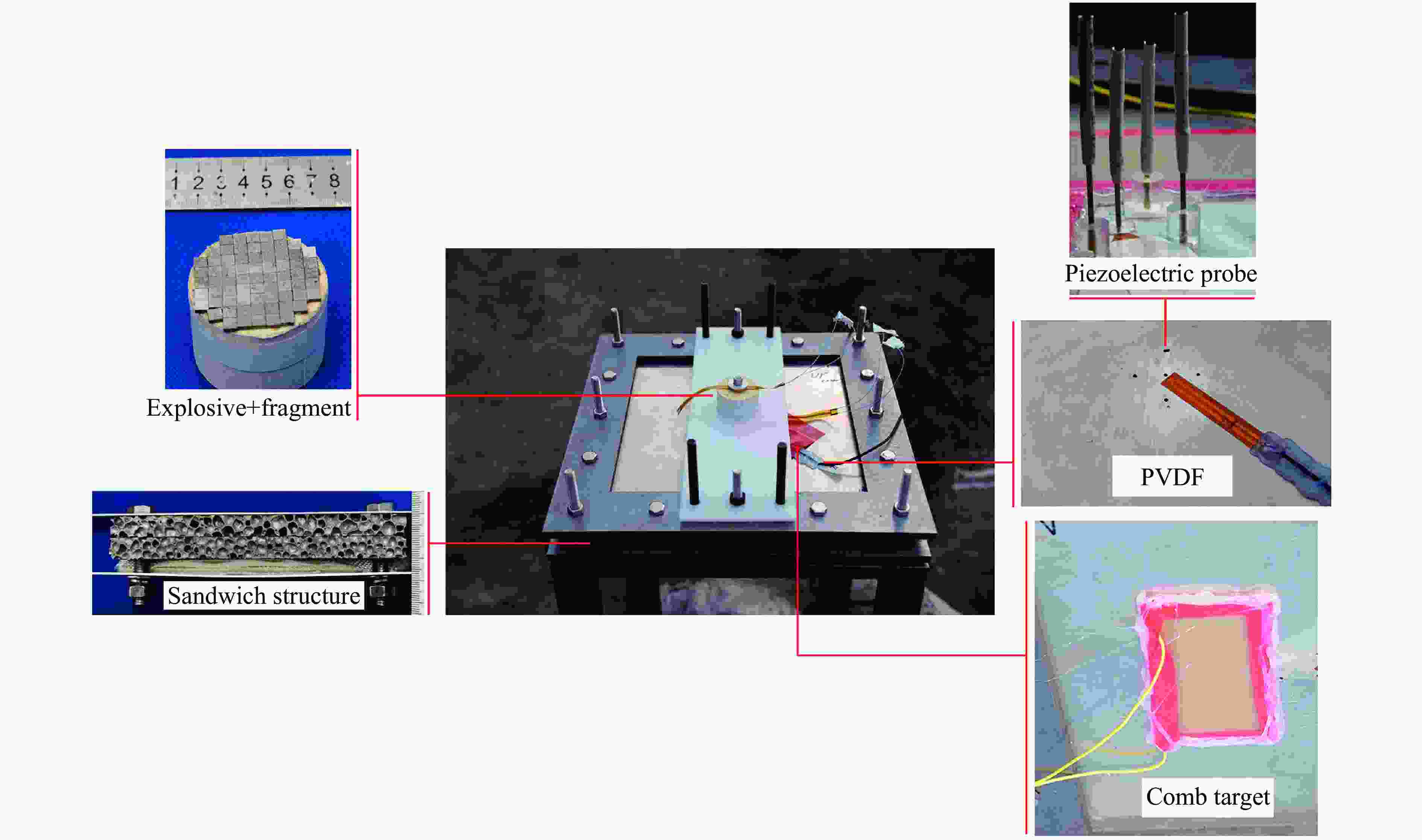
摘要: 在简易自制爆炸装置的近场爆炸中,防护结构常受到爆炸冲击波和破片的复合作用。为了提高结构的防护性能,设计并制备了含“泡沫铝/纤维”夹芯复合结构材料,通过开展“爆炸+侵彻”实验,研究复合结构在爆炸冲击波和高速破片复合作用下的失效模式,重点讨论爆炸冲击波和破片两种载荷时序性对毁伤特性的影响,并分析不同材料的吸能机理。研究结果表明:爆距的变化直接影响爆炸冲击波和破片作用的时序性,在本文讨论的工况中,当爆距大于600 mm时,破片先于冲击波作用;在冲击波和破片的复合作用下,铝面板除了破片的贯穿破坏外,还伴有局部凹陷变形,泡沫铝自身胞孔结构在冲击载荷作用下发生压溃变形和胞壁屈服碎裂,弹孔处纤维则在破片的侵彻下发生拉伸变形和断裂,并伴有高温失效;铝背板主要以瓣裂撕裂破坏为主;在两种时序性作用下,弹孔的存在削弱了冲击波对铝面板的作用,后序夹芯结构材料和铝背板的变形破坏程度较前序材料更为严重。本研究的开展对轻质复合结构材料在有限空间近爆防护领域中的应用和功能设计提供了技术依据。Abstract: In the near-field explosion of improvised explosive device, the protective structure is often subjected to the combined action of blast wave and fragments. To improve the protection performance of the structure, a composite structural material containing foamed aluminum/fiber sandwich was designed and prepared. The explosion and penetration experiment was carried out to study the failure mode of the composite structure under the combined action of explosion shock wave and high-speed fragments. In the experiment, the time for the explosive shock wave to reach the surface of the composite plate and the pressure attenuation before and after passing through the material were tested by installing PVDF pressure gauges on the upper and lower surfaces of the composite plate. Meanwhile, the time for the shock wave to reach the surface of the composite plate was measured by piezoelectric probes for the purpose of verification. The time for fragments to reach the surface of the composite plate was tested using a comb-shaped target, and the velocity attenuation of fragments after penetrating the target plate was obtained. The influence of the two loading’s timing sequence of explosion shock wave and fragment on the failure mode was discussed, and the energy absorption mechanism of different materials was analyzed. The results show that the change of detonation distance directly affects the timing sequence of the action of explosion shock wave and fragment. In the conditions discussed in this paper, when the detonation distance is greater than 600 mm, the fragment acts before the shock wave. Under the combined action of shock wave and fragment, the aluminum plate is accompanied by local sag deformation in addition to the penetration failure of fragments. The cellular structure of foamed aluminum was crushed and deformed under the impact load. The fibers at the bullet hole are stretched and fractured under the penetration of fragments, and are accompanied by high temperature failure. Under the two sequential effects, the existence of bullet holes weakens the effect of shock wave on the front aluminum plate, and the deformation and damage degree of the later sandwich structural material and the rear aluminum plate are more serious than that of the previous material. This research provides a technical basis for the application and functional design of lightweight composite structural materials in the field of near-burst protection in limited space.
-
Key words:
- sandwich structure /
- foamed aluminum /
- UHMWPE fiber /
- time sequence /
- damage characteristic
-
表 1 不同复合板夹芯组合方式和爆距设置
Table 1. Different combinations of target core and detonation distance setting
靶板编号 夹芯材料 面密度/(g∙cm−2) 爆距/mm 上层(厚1 cm) 中层(厚1 cm) 下层(12层) 1 泡沫铝 泡沫铝 SM-17纤维 1.4 200 2 泡沫铝 泡沫铝 SM-17纤维 1.4 400 3 泡沫铝 泡沫铝 SM-17纤维 1.4 600 4 泡沫铝 泡沫铝 SM-17纤维 1.4 800 表 2 时序性计算参数
Table 2. Parameters of timing calculation
$ \sqrt {2E} /({\mathrm{m}}\cdot{\mathrm{s}}^{-1})$ C/g M/g α mbe/g 2438 [22]123 26.91 0.82 91.99 表 3 冲击波和破片时序性理论计算结果
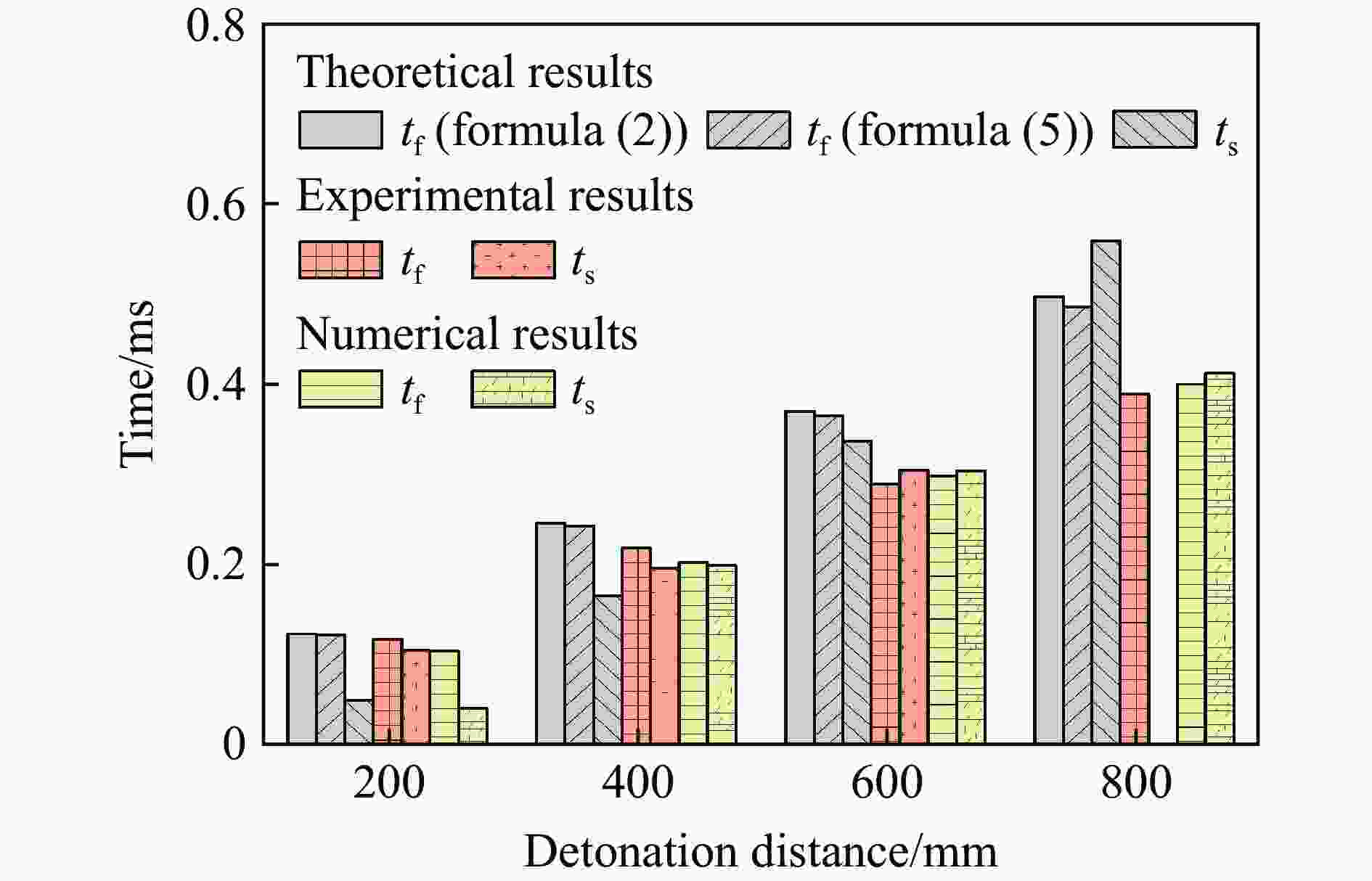
Table 3. Theoretical results of the time sequence of shock wave and fragment
爆距
R/mm重叠位置比例爆距
Rs/(m∙kg−1/3)破片初速
v0/(m∙s−1)破片到达靶板时间
tf /ms(式(2))破片到达靶板时间
tf /ms(式(5))冲击波到达靶板时间
ts /ms时序性 200 0.15[23] 1643.96 0.123 0.122 0.049 冲击波先到达 400 0.246 0.243 0.165 冲击波先到达 600 0.370 0.365 0.337 冲击波先到达 800 0.497 0.486 0.559 破片先到达 表 4 冲击波和破片时序性实验结果
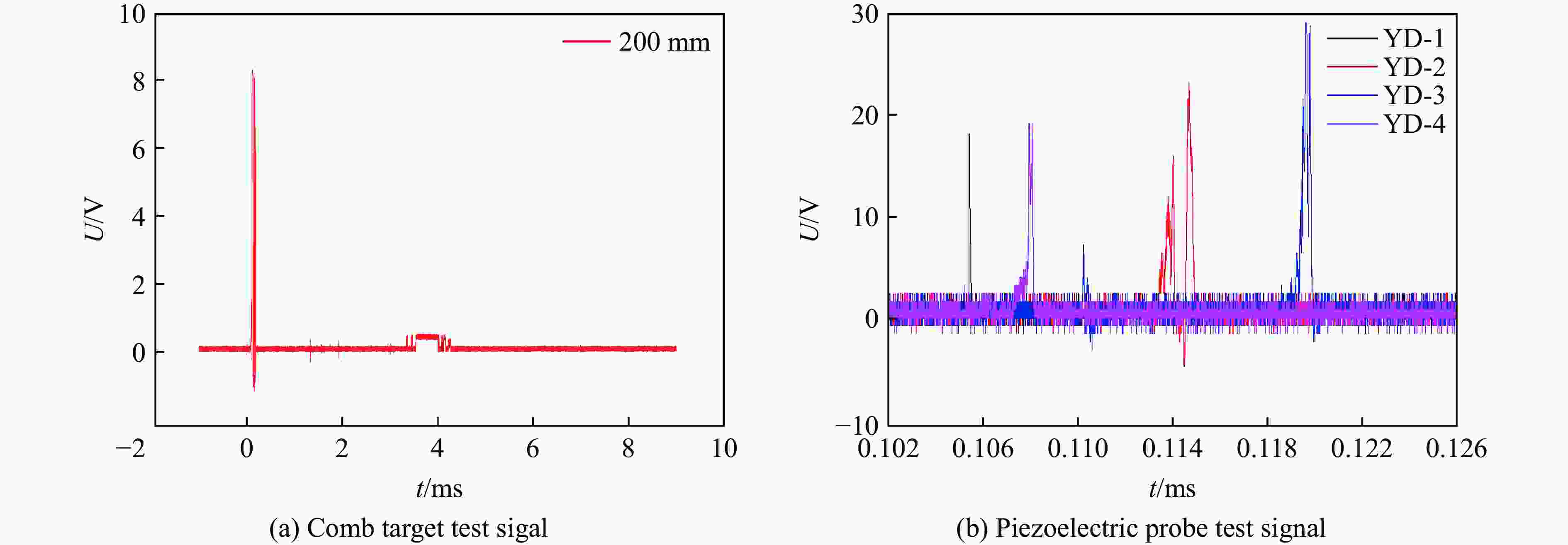
Table 4. Experimental results of the time sequence of shock wave and fragment
爆距
R/mm破片到达靶板
时间tf/ms冲击波到达靶板
时间ts/ms时序性 200 0.117 0.105 冲击波先到达 400 0.218 0.196 冲击波先到达 600 0.289 0.305 破片先到达 800 0.381 表 5 TNT炸药JWL计算参数
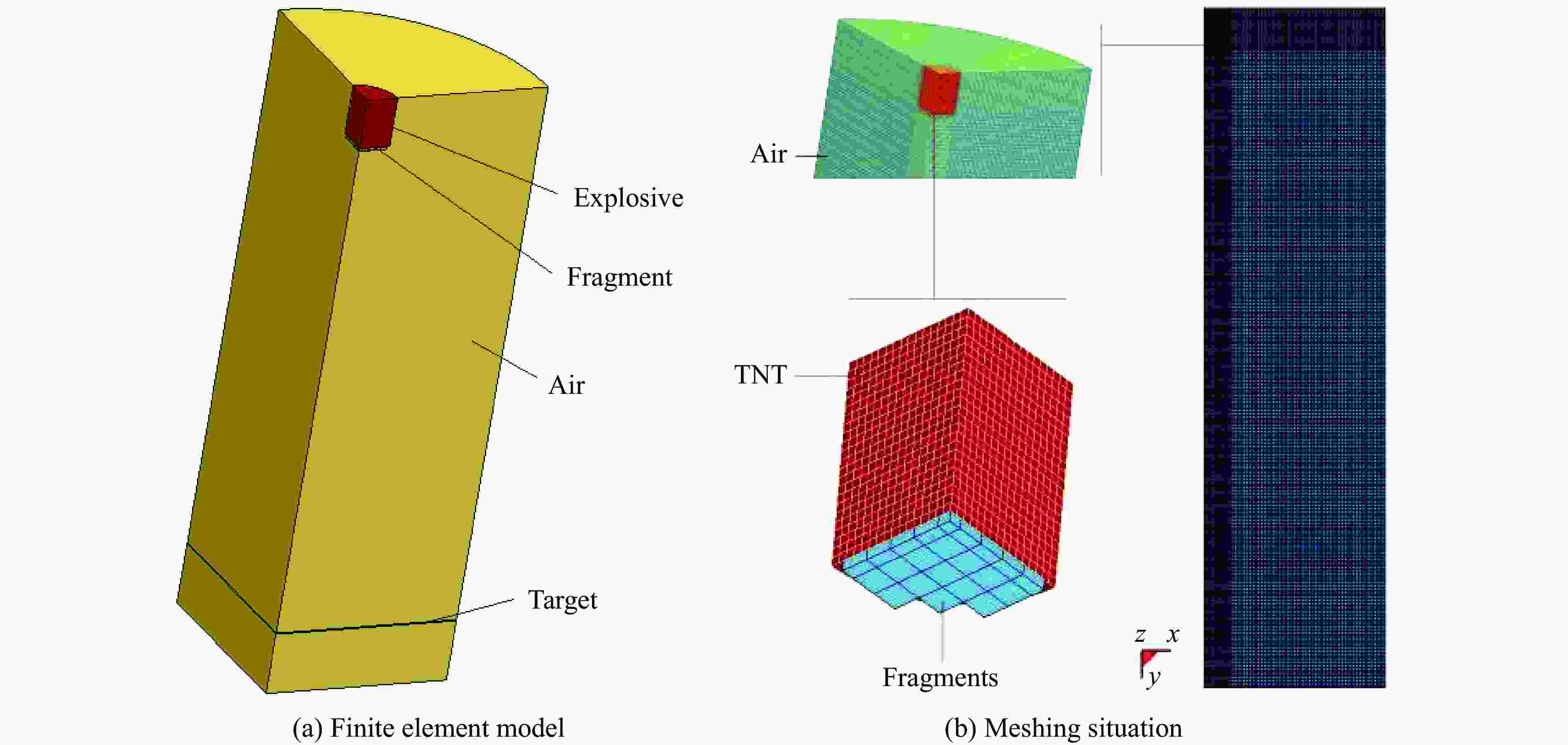
Table 5. JWL parameters of TNT explosive
密度ρ/
(kg∙m−3)爆速vD/
(m∙s−1)爆压pCJ/
GPaA/GPa B/GPa R1 R2 ω 1566 6800 21 374 3.75 4.15 0.9 0.35 表 6 冲击波和破片时序性数值模拟结果
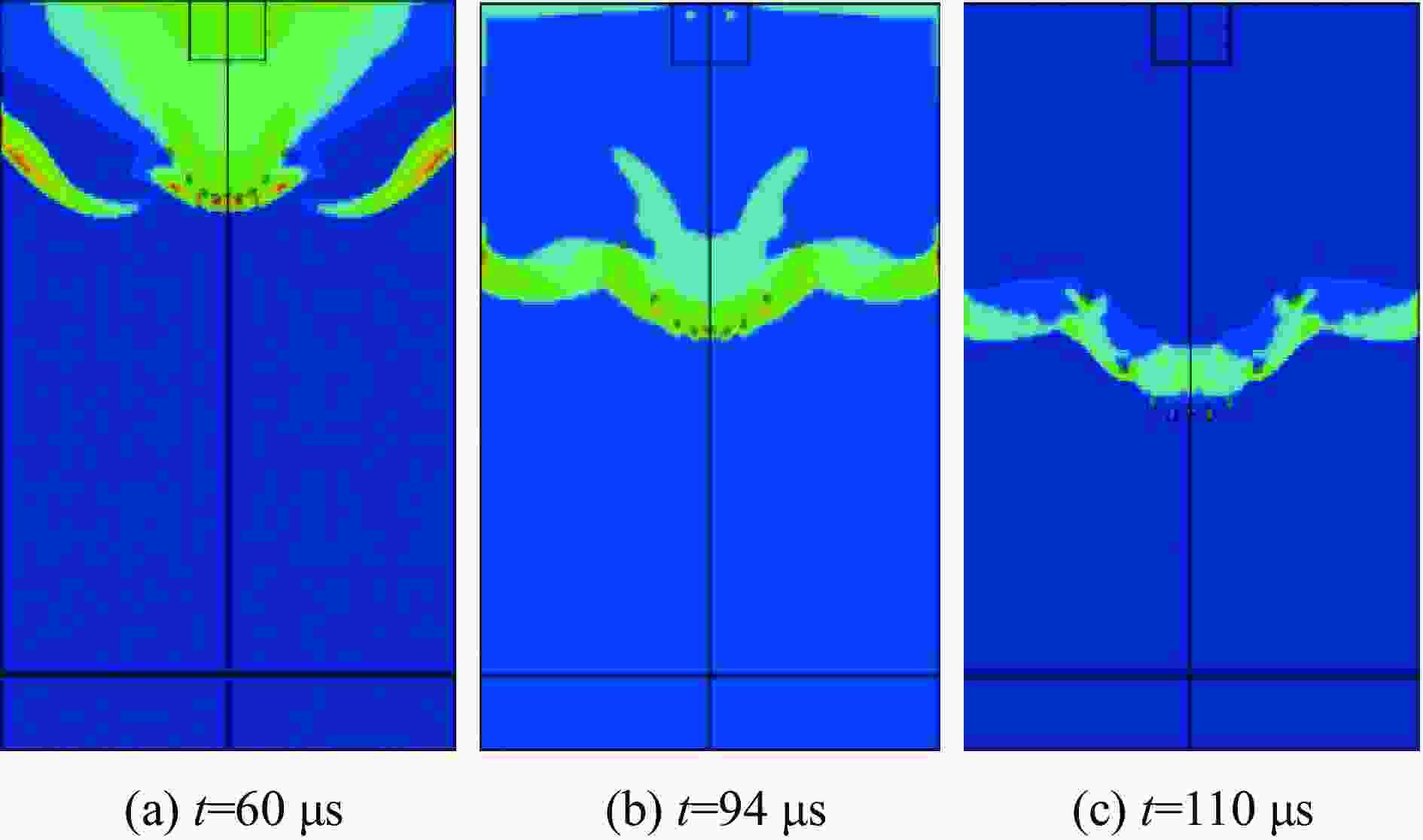
Table 6. Numerical results of the time sequence of shock wave and fragment
爆距
R/mm破片到达靶板
时间tf /ms冲击波到达靶板
时间ts/ms时序性 200 0.104 0.040 冲击波先到达 400 0.202 0.199 冲击波先到达 600 0.298 0.304 破片先到达 800 0.400 0.412 破片先到达 表 7 不同爆距下复合结构典型失效模式
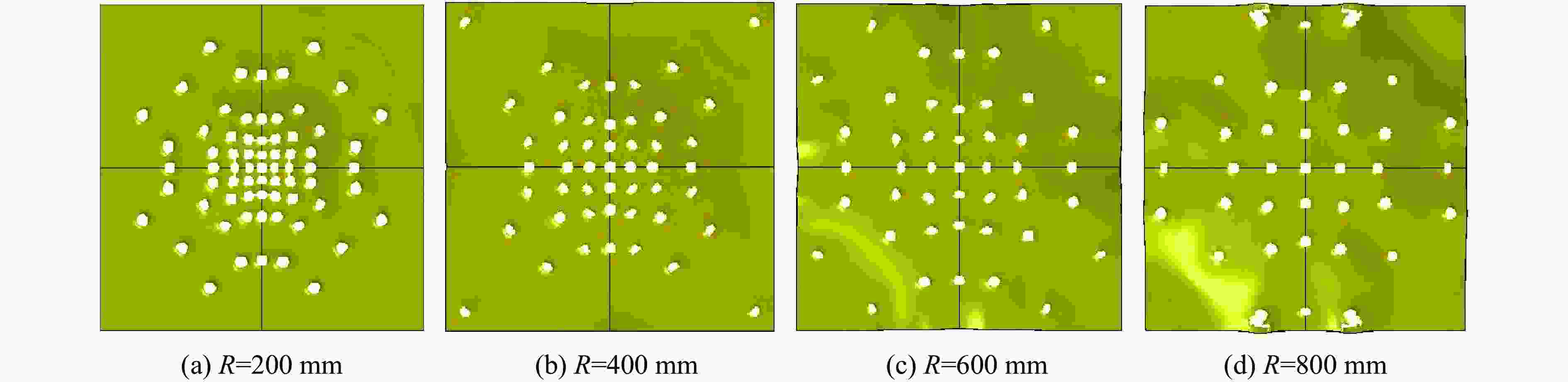
Table 7. Typical failure modes of composite structure at different detonation distances
爆距R/mm 铝面板 上层泡沫铝板 下层泡沫铝板 纤维层 铝背板 200 




400 




600 




800 




-
[1] 郑红伟, 陈长海, 侯海量, 等. 爆炸冲击波和高速破片载荷的复合作用特性及判据研究 [J]. 振动与冲击, 2019, 38(3): 24–31.ZHENG H W, CHEN C H, HOU H L, et al. Multiple impact features of blast shock waves and high-velocity fragments on clamped square plates and a criterion to judge if multiple impact happens [J]. Journal of Vibration and Shock, 2019, 38(3): 24–31. [2] 李茂, 高圣智, 侯海量, 等. 空爆冲击波与破片群联合作用下聚脲涂覆陶瓷复合装甲结构毁伤特性 [J]. 爆炸与冲击, 2020, 40(11): 111403. DOI: 10.11883/bzycj-2019-0119.LI M, GAO S Z, HOU H L, et al. Damage characteristics of polyurea coated ceramic/steel composite armor structures subjected to combined loadings of blast and high-velocity fragments [J]. Explosion and Shock Waves, 2020, 40(11): 111403. DOI: 10.11883/bzycj-2019-0119. [3] 田力, 胡建伟. 近爆冲击波和破片群联合作用下Ⅰ−Ⅴ型夹芯板的防护性能研究 [J]. 中南大学学报(自然科学版), 2018, 49(11): 2834–2837.TIAN L, HU J W. Research on protective properties of Ⅰ−Ⅴ sandwich panel under the combined loading of close-range blast wave and fragments [J]. Journal of Central South University (Science and Technology), 2018, 49(11): 2834–2837. [4] 田力, 胡建伟. Ⅰ−Ⅴ型夹芯板在近爆冲击波和破片群联合作用下防爆性能研究 [J]. 湖南大学学报(自然科学版), 2019, 49(1): 32–46. DOI: 10.16339/j.cnki.hdxbzkb.2019.01.004.TIAN L, HU J W. Research on explosion protective properties of Ⅰ−Ⅴ sandwich panel under combined loading of close-range blast wave and fragments [J]. Journal of Hunan University (Natural Sciences), 2019, 49(1): 32–46. DOI: 10.16339/j.cnki.hdxbzkb.2019.01.004. [5] NYSTRÖM U, GYLLTOFT K. Numerical studies of the combined effects of blast and fragment loading [J]. International Journal of Impact Engineering, 2009, 36(8): 995–1005. DOI: 10.1016/j.ijimpeng.2009.02.008. [6] GONG C A, CHEN Z G, YIN L K. Analysis of movement laws of fragment and shock wave from a blast fragmentation warhead [J]. Journal of Measurement Science and Instrumentation, 2015, 6(3): 218–222. DOI: 10.3969/j.issn.1674-8042.2015.03.003. [7] GRISARO H Y, DANCYGIER A N. Characteristics of combined effects of blast and fragment loading [J]. International Journal of Impact Engineering, 2018, 116(1): 51–64. DOI: 10.1016/j.ijimpeng.2018.02.004. [8] MELLEN P,SHANAHAN C,BENNETT T, et al. Blast and fragmentation loading indicative of a VBIED surrogate for structural panel response analysis [J]. International Journal of Impact Engineering, 2019, 126: 172–184. DOI: 10.1016/j.ijimpeng.2018.12.011. [9] CHU D Y, WANG Y G, YANG S L, et al. Analysis and design for the comprehensive ballistic and blast resistance of polyurea-coated steel plate [J]. Defence Technology, 2023, 19: 35–51. DOI: 10.1016/j.dt.2021.11.010. [10] 陈兴, 周兰伟, 李向东, 等. 破片式战斗部破片与冲击波相遇位置研究 [J]. 高压物理学报, 2018, 32(6): 1–9. DOI: 10.11858/gywlxb.20180591.CHEN X, ZHOU L W, LI X D, et al. Coupling action spans for air-blast waves and fragments by fragmentation warheads exploding in air [J]. Chinese Journal of High Pressure Physics, 2018, 32(6): 1–9. DOI: 10.11858/gywlxb.20180591. [11] 郑红伟, 陈长海, 李茂, 等. 空爆冲击波对高速破片绕流效应的仿真 [J]. 舰船科学技术, 2019, 41(1): 34–39.ZHENG H W, CHEN C H, LI M, et al. Research on turbulent flow of blast wave on high-velocity fragments by numerical simulation [J]. Ship Science and Technology, 22019, 41(1): 34–39. [12] 郑红伟, 陈长海, 李茂, 等. 空爆冲击波对不同形状破片的绕流作用仿真分析 [J]. 舰船科学技术, 2019, 41(3): 31–36.ZHENG H W, CHEN C H, LI M, et al. Research on turbulent flow of blast wave on high-velocity fragments in different shapes by numerical simulation [J]. Ship Science and Technology, 2019, 41(3): 31–36. [13] 蔡林刚, 杜志鹏, 李晓彬, 等. 爆炸冲击波与破片联合作用下泡沫夹芯板的毁伤特性研究 [J]. 武汉理工大学学报(交通科学与工程版), 2020, 44(2): 316–320.CAI L G, DU Z P, LI X B, et al. Study on damage characteristic of foam sandwich panel under combined action of explosion shock wave and fragments [J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2020, 44(2): 316–320. [14] 侯俊亮, 蒋建伟, 李应波, 等. 杀爆战斗部破片和冲击波对目标的耦合作用 [J]. 火炸药学报, 2020, 43(3): 335–340. DOI: 10.14077/j.issn.1007-7812.201909009.HOU J L, JIANG J W, LI Y B, et al. Study on the coupling effect of fragments and shock wave of the blast-fragmentation warhead on typical targets [J]. Chinese Journal of Explosives & Propellants, 2020, 43(3): 335–340. DOI: 10.14077/j.issn.1007-7812.201909009. [15] 王智, 常利军, 黄星源, 等. 爆炸冲击波与破片联合作用下防弹衣复合结构防护效果的数值模拟 [J]. 爆炸与冲击, 2023, 43(6), 063202. DOI: 10.11883/bzycj-2022-0515.WANG Z, CHANG L J, HUANG X Y, et al. Simulation on the defending effect of composite structure of body armor under the combined action of blast wave and fragments [J]. Explosion and Shock Waves, 2023, 43(6): 063202. DOI: 10.11883/bzycj-2022-0515. [16] 周猛, 梁民族, 林玉亮. 冲击波-破片联合载荷对固支方板的耦合作用机理 [J]. 兵工学报, 2023, 44(S1): 99–106. DOI: 10.12382/bgxb.2023.0732.ZHOU M, LIANG M Z, LIN Y L. Mechanism of coupling effect of shock wave and fragments on clamped square plate [J]. Acta Armamentarii, 2023, 44(S1): 99–106. DOI: 10.12382/bgxb.2023.0732. [17] ZHOU N, WANG J X, JIANG D K, et al. Study on the failure mode of a sandwich composite structure under the combined actions of explosion shock wave and fragments [J]. Materials and Design, 2020, 196(109): 1–15. DOI: 10.1016/j.matdes.2020.109166. [18] KONG X S, WU W G, LI J, et al. A numerical investigation on explosive fragmentation of metal casing using Smoothed Particle Hydrodynamic method [J]. Materials and Design, 2013, 51: 729–741. DOI: 10.1016/j.matdes.2013.04.041. [19] 孙业斌. 爆炸作用与装药设计 [M]. 北京: 国防工业出版社, 1987: 47–55. [20] 安振涛, 王超, 甄建伟, 等. 常规弹药爆炸破片和冲击波作用规律理论研究 [J]. 爆破, 2012, 29(1): 15–18. DOI: 10.3963/j.issn.1001-487X.2012.01.004.AN Z T, WANG C, ZHEN J W, et al. Theoretical research on action law of fragment and shock wave of traditional ammunition explosion [J]. Blasting, 2012, 29(1): 15–18. DOI: 10.3963/j.issn.1001-487X.2012.01.004. [21] 梁为民, 张晓忠, 梁仕发, 等. 结构内爆炸破片与冲击波运动规律实验研究 [J]. 兵工学报, 2009(S2): 223–227.LIANG W M, ZHANG X Z, LIANG S F, et al. Experimental research on motion law of fragment and shock wave under the condition of internal explosion [J]. Acta Armamentarii, 2009(S2): 223–227. [22] 黄正祥, 祖旭东. 终点效应 [M]. 北京: 科学出版社, 2014: 85. [23] 甘露, 陈力, 宗周红, 等. 近距离爆炸比例爆距的界定标准及荷载类型 [J]. 爆炸与冲击, 2021, 41(6): 064902. DOI: 10.11883/bzycj-2020-0194.GAN L, CHEN L, ZONG Z H, et al. Definition of scaled distance of close-in explosion and blast load calculation model [J]. Explosion and Shock Waves, 2021, 41(6): 064902. DOI: 10.11883/bzycj-2020-0194. [24] LEPPÄNEN J. Experiments and numerical analyses of blast and fragment impacts on concrete [J]. International Journal of Impact Engineering, 2005, 31(7): 843–860. DOI: 10.1016/j.ijimpeng.2004.04.012. [25] CAI S P, LIU J, LI C P. Dynamic response of sandwich panels with multi-layered aluminum foam/UHMWPE laminate cores under air blast loading [J]. International Journal of Impact Engineering, 2020, 138: 1–16. DOI: 10.1016/j.ijimpeng.2019.103475. -






 下载:
下载: