Fast estimation of blast loading in complex structures based on Bayesian deep learning
-
摘要: 对于复杂结构的爆炸载荷估计,传统数值模拟方法计算耗时长,而基于神经网络的快速估计仅能进行点估计,无法给出结果的置信度。为此,结合贝叶斯理论和深度学习,构建了复杂结构爆炸载荷快速估计的贝叶斯深度学习方法。通过开源数值模拟软件,计算了爆炸当量、位置、速度等参数大范围变化下复杂结构的爆炸载荷数据,基于贝叶斯理论将深度学习模型参数视为随机变量,利用变分贝叶斯推断高效训练模型,在保证爆炸载荷快速估计精度的同时,赋予模型不确定性量化的能力。结果表明,该方法对训练数据以外的爆炸载荷快速估计的误差约为12.2%,置信区间涵盖真实值的百分比超过81.6%,单点爆炸载荷估计时间不超过20 ms。该方法是实现复杂结构爆炸载荷快速、可信估计的新方法。Abstract: For the estimation of blast loading in complex structures, traditional numerical simulation methods were computationally intensive whereas rapid estimation methods based on neural networks can only provide estimates at local points without providing confidence intervals for the predicted results. To achieve fast and reliable estimation of the blast loading in complex structures, Bayesian theory was combined with deep learning to develop a Bayesian deep learning approach for rapid estimation of blast loading in complex structures. The approach initially utilized open-source numerical simulation software to generate a dataset of blast loading in complex structures, encompassing a wide range of parameters such as explosion equivalents, locations, and velocities. During this process, mesh sizes that balanced computational accuracy and speed were determined through mesh sensitivity analysis and the verification of the numerical simulation accuracy. Then, the deep learning model was extended into a Bayesian deep learning model based on Bayesian theory. By introducing probability distributions over the weights of the neural network, the model parameters were treated as random variables. Variational Bayesian inference was then employed to efficiently train the model, ensuring the accuracy of rapid blast loading estimation while also equipping the model with the ability to quantify uncertainty. Finally, metrics such as mean absolute percentage error (MAPE), normalized mean prediction interval width (NMPIW) and prediction interval coverage probability (PICP) were adopted to quantitatively assess the model's estimated accuracy and the precision of the uncertainty quantification. Additionally, an error decomposition of the estimation results was conducted to analyze model’s performance based on target parameters and scaled distance. The results indicate that the proposed method achieved an estimation error of 12.2% on the test set, with a confidence interval covering over 81.6% of true values, and less than 20 milliseconds of the estimation time for a single sample point. This method provides a novel approach for fast and accurate estimation of blast loading in complex structures with sufficient confidence for the estimation results.
-
Key words:
- complex structures /
- blast loading /
- Bayesian deep learning /
- quantization of uncertainty
-
表 1 爆源参数的范围
Table 1. The range of explosion source parameters
爆源参数 符号 单位 参数范围 当量 Q kg (200, 2000 )爆心距 R m (40, 100) 起爆速度 U m/s (0, 1020 )表 2 经验常数的取值
Table 2. The values of empirical constants
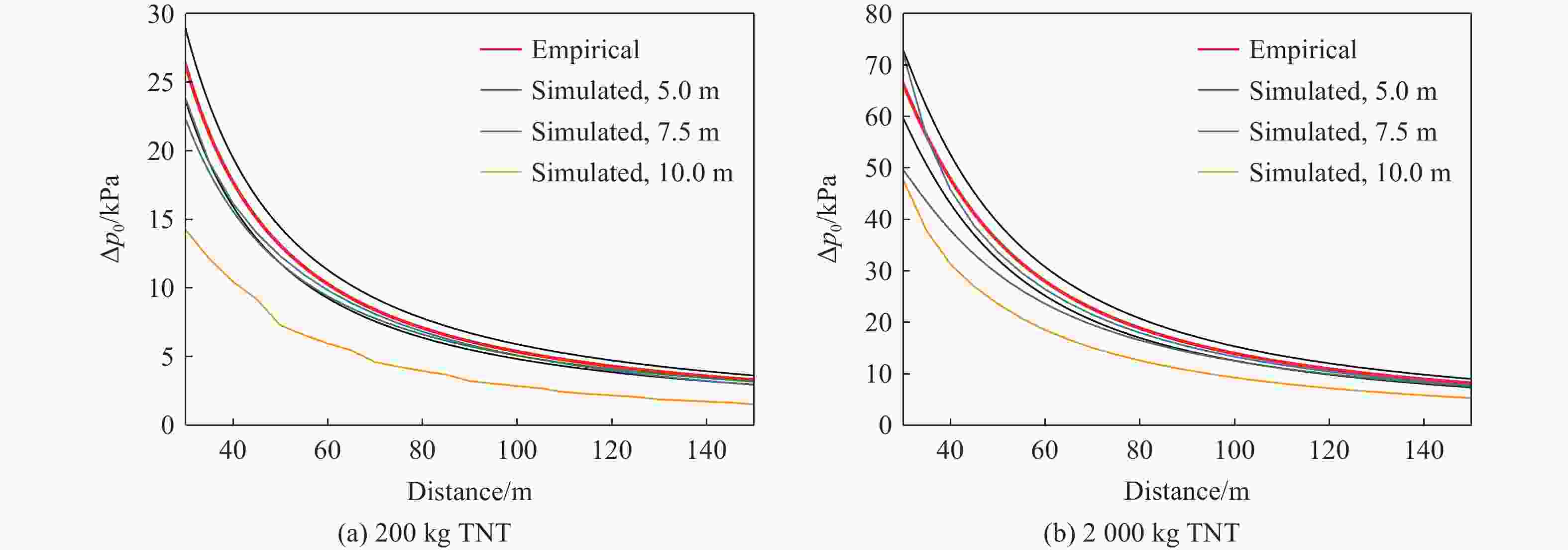
A/TPa B/TPa R1 R2 λ1 e/(TJ·m−3) ρ0/(kg·m−3) 609.77 12.95 4.50 0.9 0.25 9.0 1 630 表 3 不同背景网格设置下数值模拟所需的计算时间
Table 3. Calculation time required for numerical simulation with different background grid settings
背景网格尺寸/m 5.0 7.5 10.0 计算时间/h 10 2 1 表 4 待调节的超参数及其取值范围
Table 4. The hyperparameter to be adjusted and the corresponding range
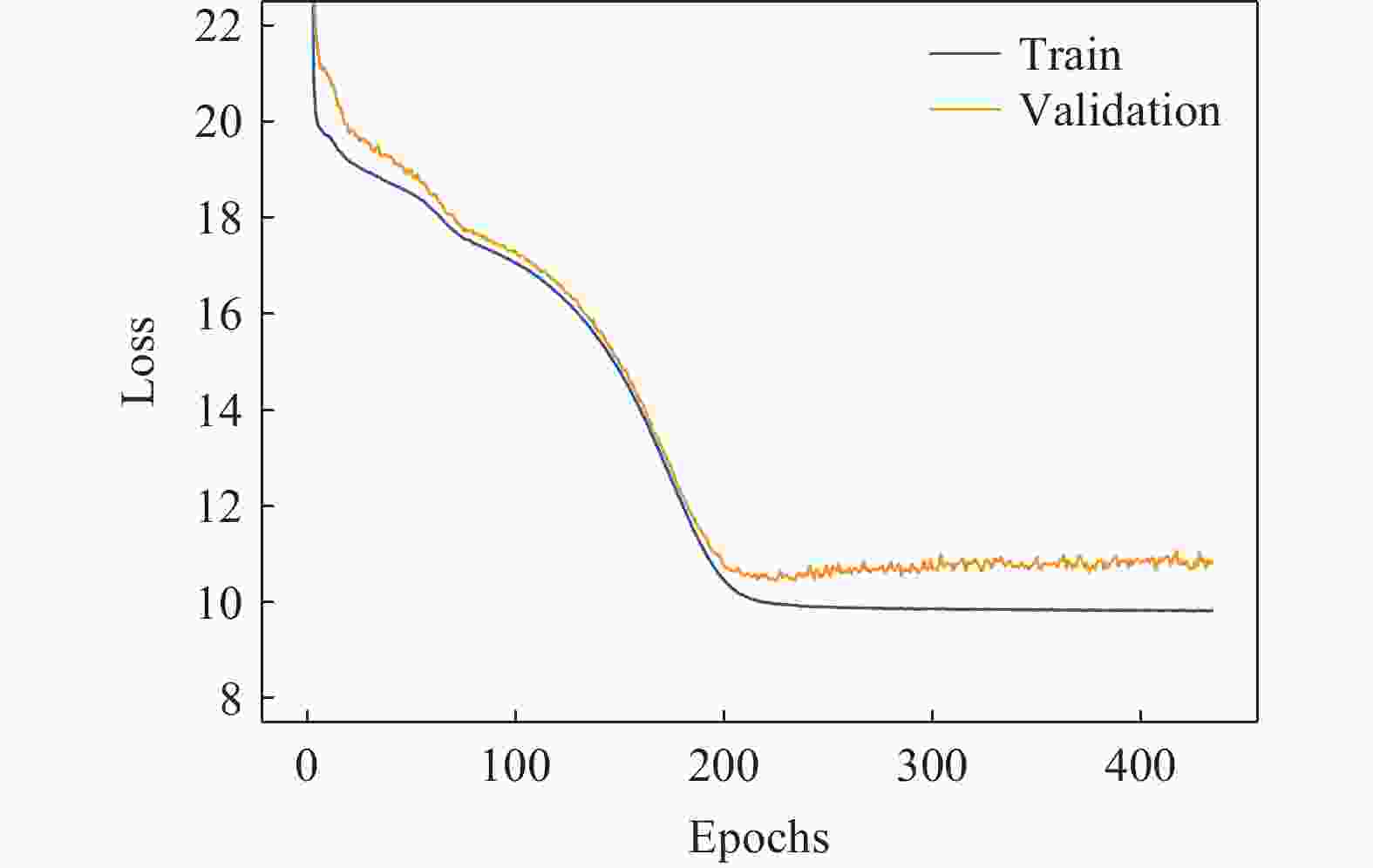
神经网络层数 每层神经元数 激活函数 学习率 2~8 16, 32, 64, 128, 256 ReLU, Leaky ReLU 0.001, 0.005, 0.010 表 5 模拟平台的参数
Table 5. Parameters of the simulation platform
平台 处理器 内存 操作系统 天河二号超级计算中心 2×12 Intel Xeon E5- 2692 v2/单节点128 GB/单节点 Linux lon26 3.10.0-514.el7.x86_64 本地台式机 AMD Ryzen7 3700x8-Core八核 32 GB Windows10 表 6 超压峰值的估计精度和不确定性
Table 6. The estimation accuracy and uncertainty of the peak overpressure
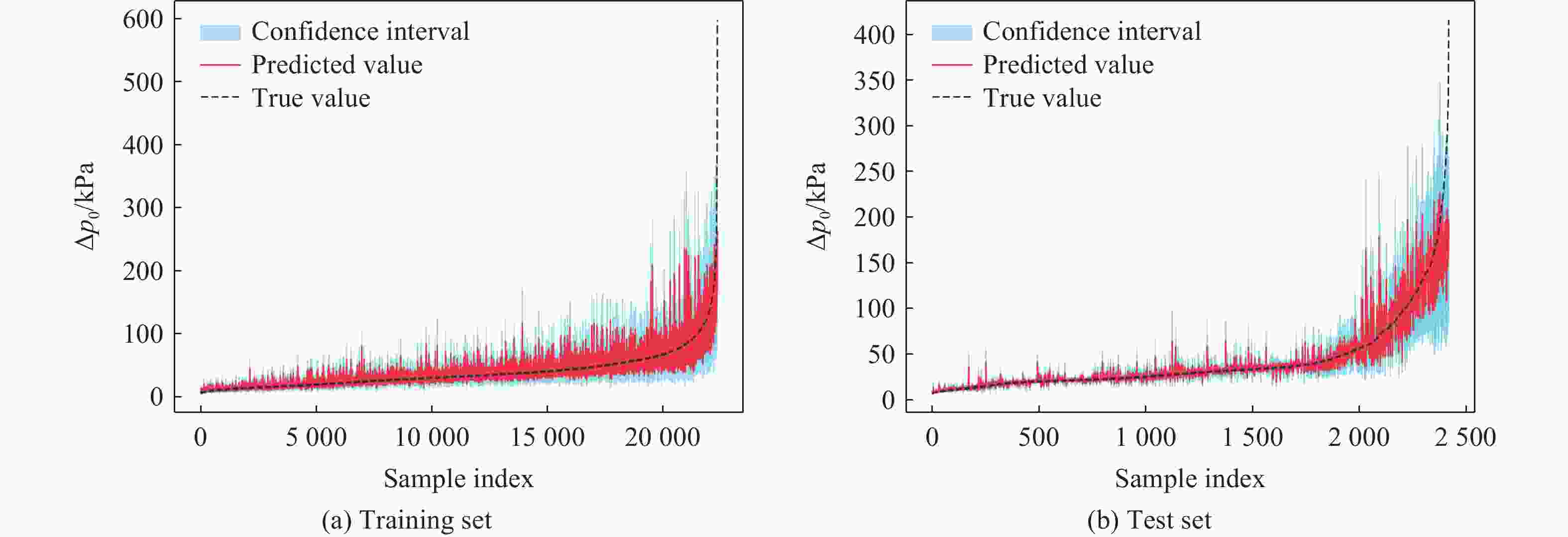
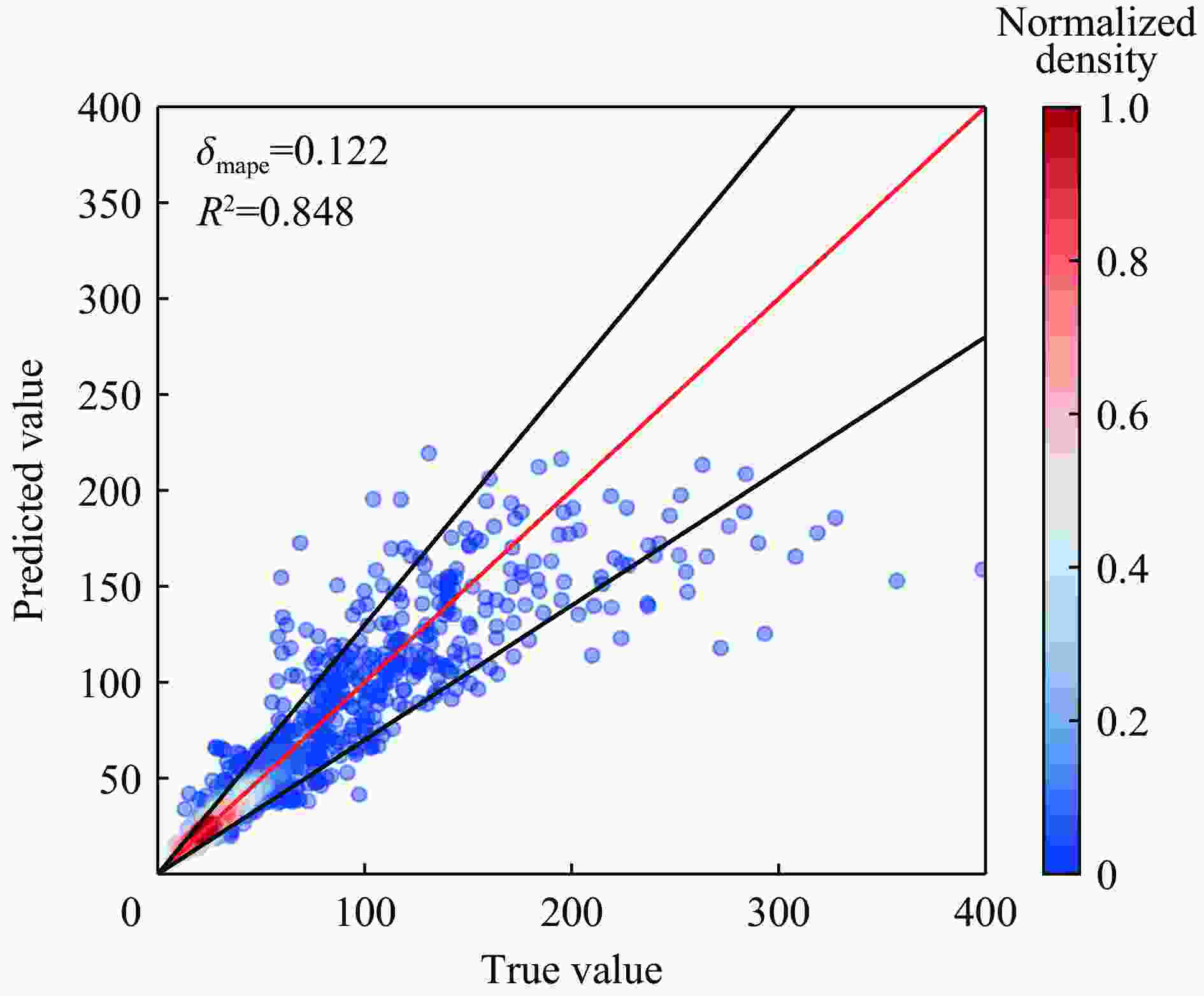
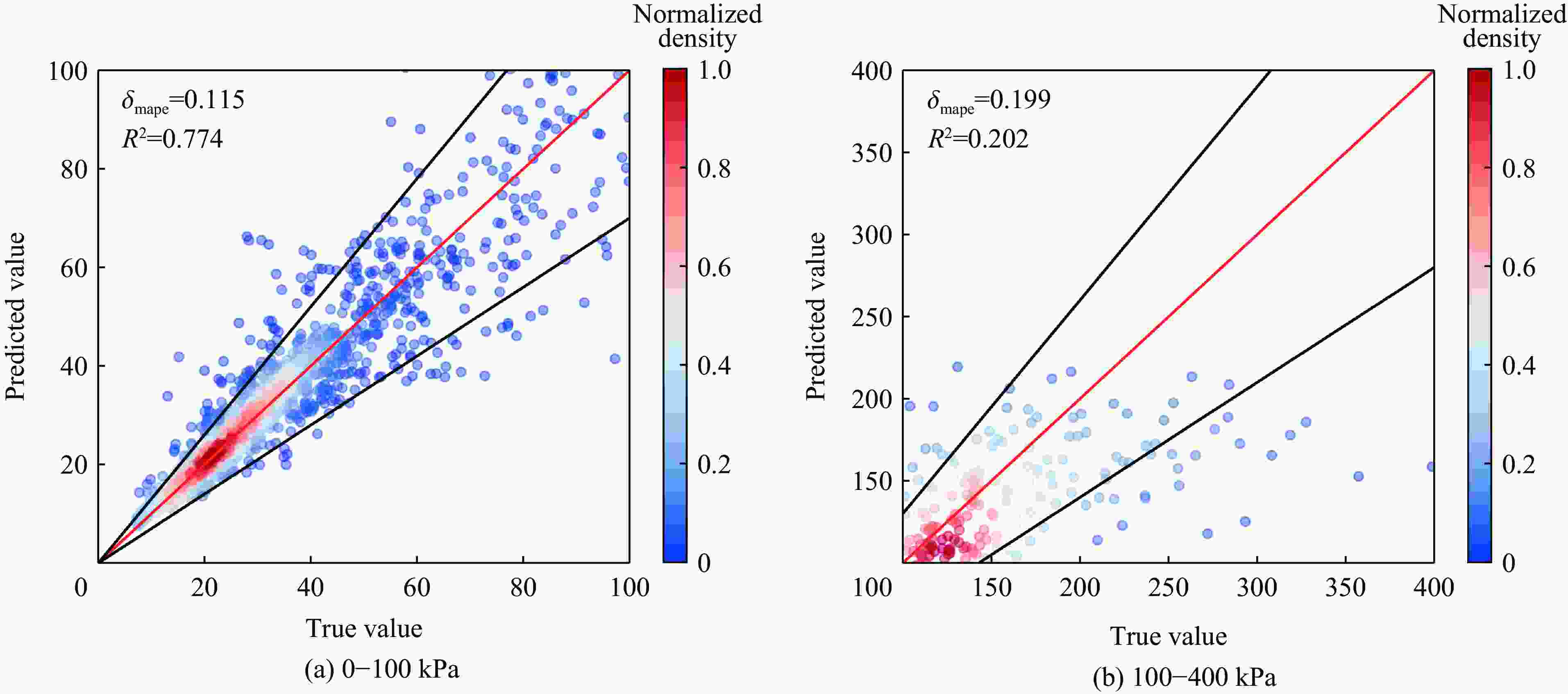
估计精度 不确定性 δmape R2 ppicp wnmpiw 训练集 测试集 训练集 测试集 训练集 测试集 训练集 测试集 0.104 0.122 0.834 0.830 0.921 0.816 0.041 0.057 表 7 基于目标范围的误差分解
Table 7. Error decomposition based on target range
超压峰值/kPa 样本数量 δmape/% φ/% 0 < δmape ≤ 10% 10% < δmape ≤ 20% 20% < δmape ≤ 30% 30% < δmape ≤ 50% δmape ≤ 50% [0, 50] 1927 10.173 66.27 21.33 7.16 3.68 98.44 (50, 100] 282 20.492 37.94 24.82 15.60 16.67 95.03 (100, 150] 124 17.714 41.13 20.97 18.55 14.52 95.15 (150, 400] 83 25.008 18.07 18.07 26.51 32.53 95.18 表 8 基于比例距离的误差分解
Table 8. Error decomposition based on scaled distance
比例距离/$ (\mathrm{m}\mathrm{\cdot kg}^{-{1}/{3}}) $ 样本数量 δmape/% φd/% 0 < δmape ≤ 10% 10% < δmape ≤ 20% 20% < δmape ≤ 30% 30% < δmape ≤ 50% δmape ≤ 50% (3, 5] 388 21.114 34.79 23.97 16.75 18.04 93.55 (5, 7] 963 13.091 57.22 23.88 8.72 7.79 97.61 (7, 10] 949 8.389 71.97 18.12 6.43 2.85 99.37 -
[1] SMITH P D, ROSE T A. Blast wave propagation in city streets—an overview [J]. Progress in Structural Engineering and Materials, 2006, 8(1): 16–28. DOI: 10.1002/pse.209. [2] RATCLIFF A, RIGBY S, CLARKE S, et al. A review of blast loading in the urban environment [J]. Applied Sciences, 2023, 13(9): 5349. DOI: 10.3390/app13095349. [3] SHI Y C, LIU S Z, LI Z X, et al. Review on quick safety assessment of building structures in complex urban environment after extreme explosion events [J]. International Journal of Protective Structures, 2023, 14(3): 438–458. DOI: 10.1177/20414196221104146. [4] PANNELL J J, PANOUTSOS G, COOKE S B, et al. Predicting specific impulse distributions for spherical explosives in the extreme near-field using a Gaussian function [J]. International Journal of Protective Structures, 2021, 12(4): 437–459. DOI: 10.1177/2041419621993492. [5] REMENNIKOV A M, ROSE T A. Predicting the effectiveness of blast wall barriers using neural networks [J]. International Journal of Impact Engineering, 2007, 34(12): 1907–1923. DOI: 10.1016/j.ijimpeng.2006.11.003. [6] REMENNIKOV A M, MENDIS P A. Prediction of airblast loads in complex environments using artificial neural networks [M]. Edinburgh: WIT Press, 2006: 269–78. [7] DENNIS A A, PANNELL J J, SMYL D J, et al. Prediction of blast loading in an internal environment using artificial neural networks [J]. International Journal of Protective Structures, 2021, 12(3): 287–314. DOI: 10.1177/2041419620970570. [8] FLOOD I, BEWICK B T, SALIM H A, et al. A neural network approach to modeling the effects of barrier walls on blast wave propagation PREPRINT [J]. Applied Research Associates Inc Tyndall Afb Fl, 2008: 0011. [9] FLOOD I, BEWICK B T, DINAN R J, et al. Modeling blast wave propagation using artificial neural network methods [J]. Advanced Engineering Informatics, 2009, 23(4): 418–423. DOI: 10.1016/j.aei.2009.06.005. [10] BEWICK B, FLOOD I, CHEN Z. A neural-network model-based engineering tool for blast wall protection of structures [J]. International Journal of Protective Structures, 2011, 2(2): 159–176. DOI: 10.1260/2041-4196.2.2.159. [11] DENNIS A A, RIGBY S E. The direction-encoded neural network: a machine learning approach to rapidly predict blast loading in obstructed environments [J]. International Journal of Protective Structures, 2024, 15(3): 455–483. DOI: 10.1177/20414196231177364. [12] PANNELL J J, RIGBY S E, PANOUTSOS G. Physics-informed regularisation procedure in neural networks: an application in blast protection engineering [J]. International Journal of Protective Structures, 2022, 13(3): 555–578. DOI: 10.1177/20414196211073501. [13] PANNELL J J, RIGBY S E, PANOUTSOS G. Application of transfer learning for the prediction of blast impulse [J]. International Journal of Protective Structures, 2023, 14(2): 242–262. DOI: 10.1177/20414196221096699. [14] KANG M A, PARK C H. Prediction of peak pressure by blast wave propagation between buildings using a conditional 3D convolutional neural network [J]. IEEE Access, 2023, 11: 26114–26124. DOI: 10.1109/ACCESS.2023.3257345. [15] HUANG Y, ZHU S J, CHEN S W. Deep learning-driven super-resolution reconstruction of two-dimensional explosion pressure fields [J]. Journal of Building Engineering, 2023, 78: 107620. DOI: 10.1016/j.jobe.2023.107620. [16] LI Q L, WANG Y, SHAO Y D, et al. A comparative study on the most effective machine learning model for blast loading prediction: from GBDT to Transformer [J]. Engineering Structures, 2023, 276: 115310. DOI: 10.1016/j.engstruct.2022.115310. [17] LI J D, LI Q L, HAO H, et al. Prediction of BLEVE blast loading using CFD and artificial neural network [J]. Process Safety and Environmental Protection, 2021, 149: 711–723. DOI: 10.1016/j.psep.2021.03.018. [18] LI Q L, WANG Y, CHEN W S, et al. Machine learning prediction of BLEVE loading with graph neural networks [J]. Reliability Engineering & System Safety, 2024, 241: 109639. DOI: 10.1016/j.ress.2023.109639. [19] LI Q L, WANG Y, LI L, et al. Prediction of BLEVE loads on structures using machine learning and CFD [J]. Process Safety and Environmental Protection, 2023, 171: 914–925. DOI: 10.1016/j.psep.2023.02.008. [20] ZUO K J, YE Z Y, ZHANG W W, et al. Fast aerodynamics prediction of laminar airfoils based on deep attention network [J]. Physics of Fluids, 2023, 35(3): 037127. DOI: 10.1063/5.0140545. [21] DOU Z H, GAO C Q, ZHANG W W, et al. Nonlinear aeroelastic prediction in transonic buffeting flow by deep neural network [J]. AIAA Journal, 2023, 61(6): 2412–2429. DOI: 10.2514/1.J061946. [22] HU J W, DOU Z H, ZHANG W W. Fast fluid–structure interaction simulation method based on deep learning flow field modeling [J]. Physics of Fluids, 2024, 36(4): 045106. DOI: 10.1063/5.0200188. [23] ZHANG Q, WANG X, YANG D G, et al. Data-driven prediction of aerodynamic noise of transonic buffeting over an airfoil [J]. Engineering Analysis with Boundary Elements, 2024, 163: 549–561. DOI: 10.1016/j.enganabound.2024.04.006. [24] KOU J Q, ZHANG W W. Data-driven modeling for unsteady aerodynamics and aeroelasticity [J]. Progress in Aerospace Sciences, 2021, 125: 100725. DOI: 10.1016/j.paerosci.2021.100725. [25] VALGER S A, FEDOROVA N N, FEDOROV A V. Numerical simulation of blast action on civil structures in urban environment [C]//IOP Conference Series: Materials Science and Engineering. IOP Publishing, 2017, 245(6): 062018. DOI: 10.1088/1757-899X/245/6/062018. [26] 聂源, 蒋建伟, 李梅. 球形装药动态爆炸冲击波超压场计算模型 [J]. 爆炸与冲击, 2017, 37(5): 951–956. DOI: 10.11883/1001-1455(2017)05-0951-06.NIE Y, JIANG J W, LI M. Overpressure calculation model of sphere charge blasting with moving velocity [J]. Explosion and Shock Waves, 2017, 37(5): 951–956. DOI: 10.11883/1001-1455(2017)05-0951-06. [27] WANG H, YEUNG D Y. Towards Bayesian deep learning: a framework and some existing methods [J]. IEEE Transactions on Knowledge and Data Engineering, 2016, 28(12): 3395–3408. DOI: 10.1109/TKDE.2016.2606428. [28] JOSPIN L V, LAGA H, BOUSSAID F, et al. Hands-on Bayesian neural networks—a tutorial for deep learning users [J]. IEEE Computational Intelligence Magazine, 2022, 17(2): 29–48. DOI: 10.1109/MCI.2022.3155327. [29] ABDAR M, POURPANAH F, HUSSAIN S, et al. A review of uncertainty quantification in deep learning: techniques, applications and challenges [J]. Information Fusion, 2021, 76: 243–297. DOI: 10.1016/j.inffus.2021.05.008. [30] PSAROS A F, MENG X H, ZOU Z R, et al. Uncertainty quantification in scientific machine learning: methods, metrics, and comparisons [J]. Journal of Computational Physics, 2023, 477: 111902. DOI: 10.1016/j.jcp.2022.111902. -






 下载:
下载: