Numerical modeling of the energy dissipation and fragmentation of copper-bearing rock under impact load
-
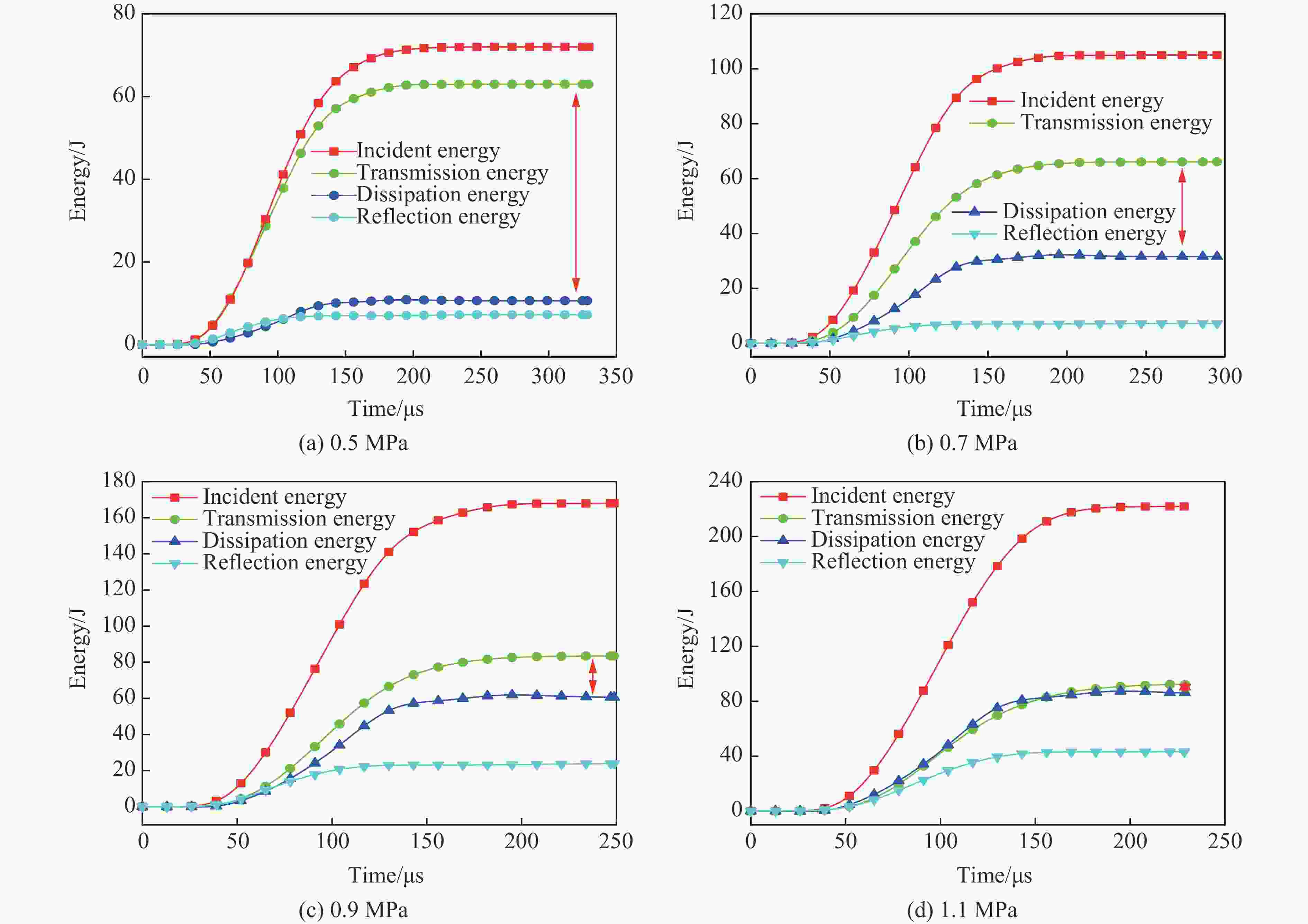
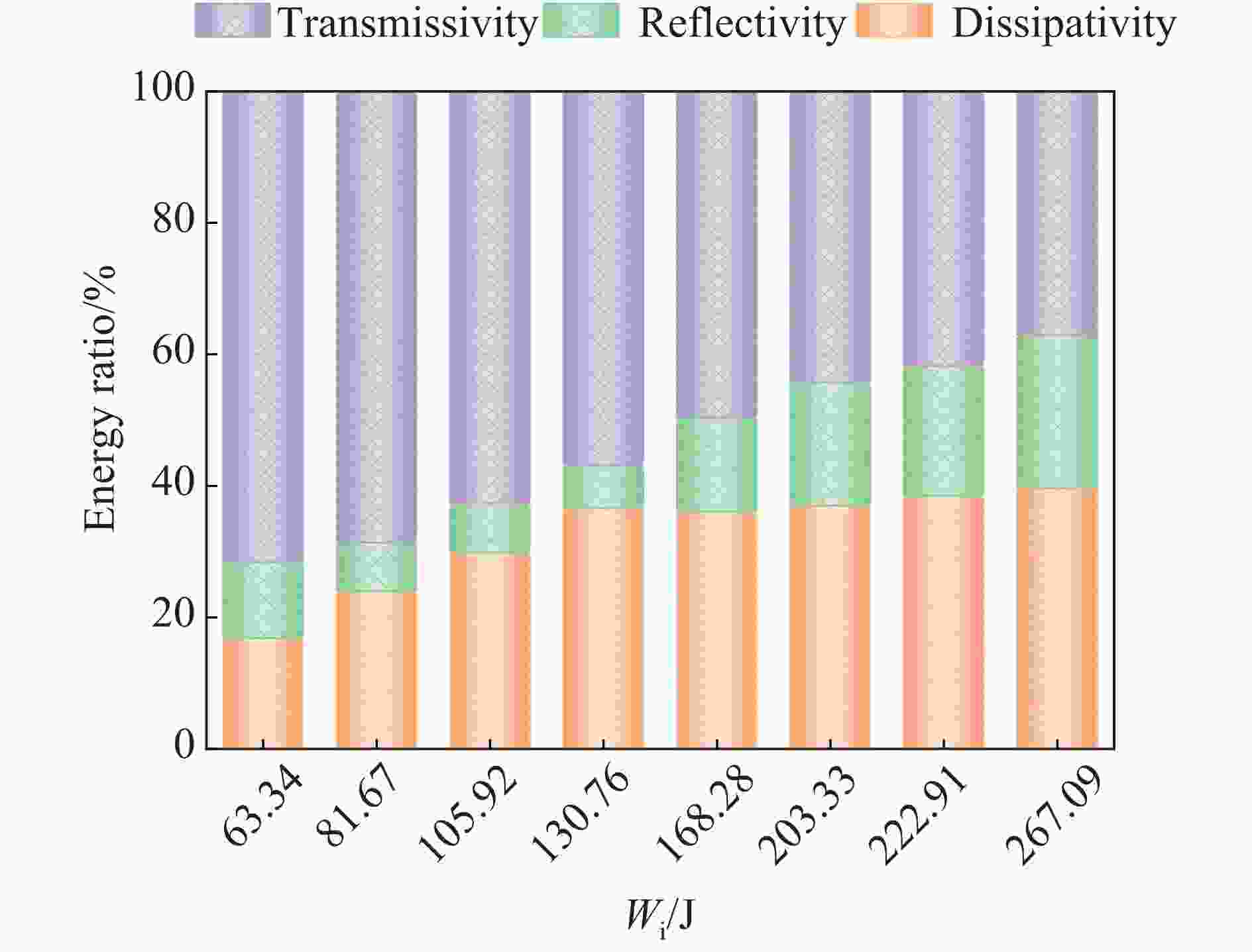
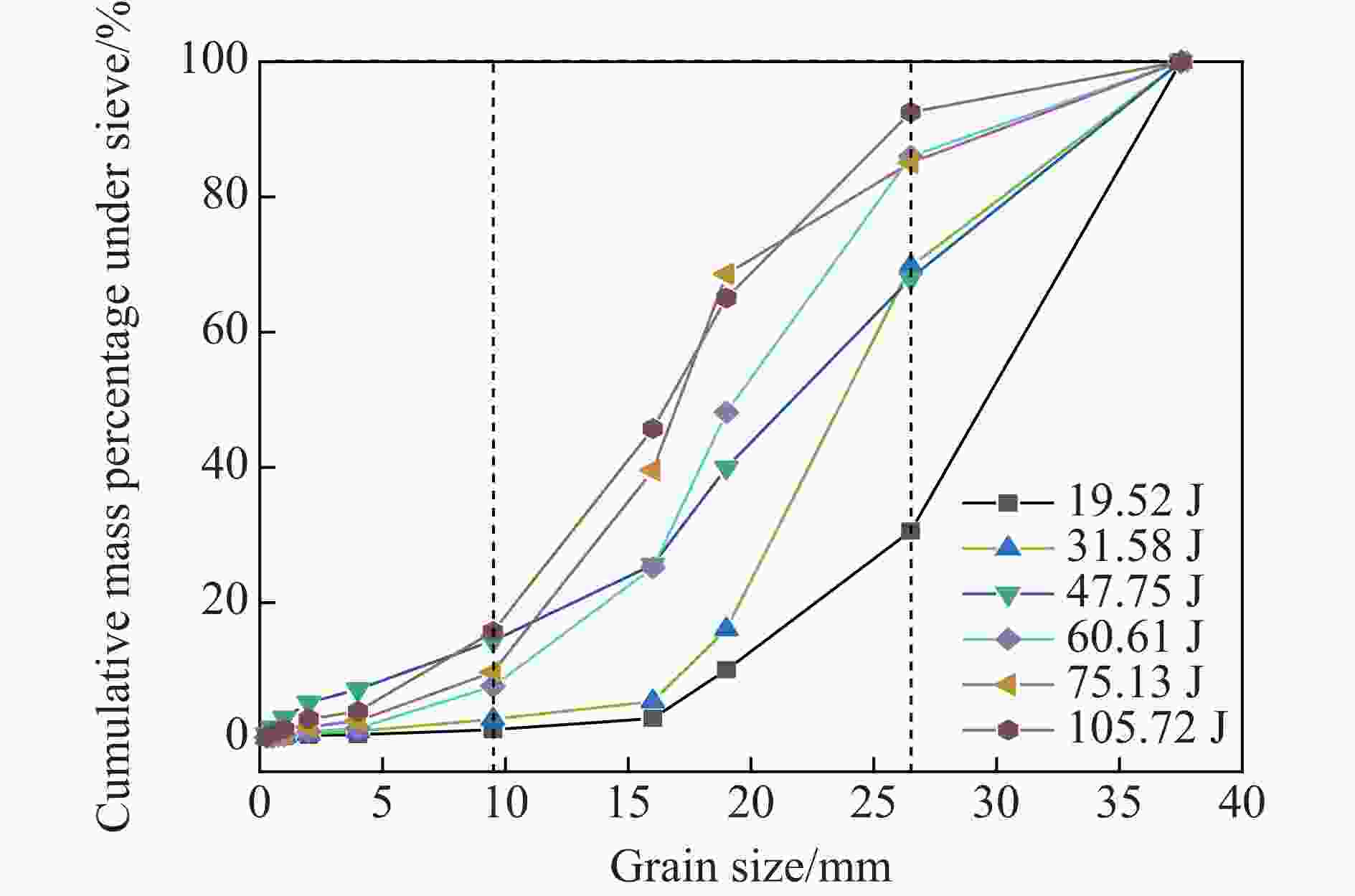
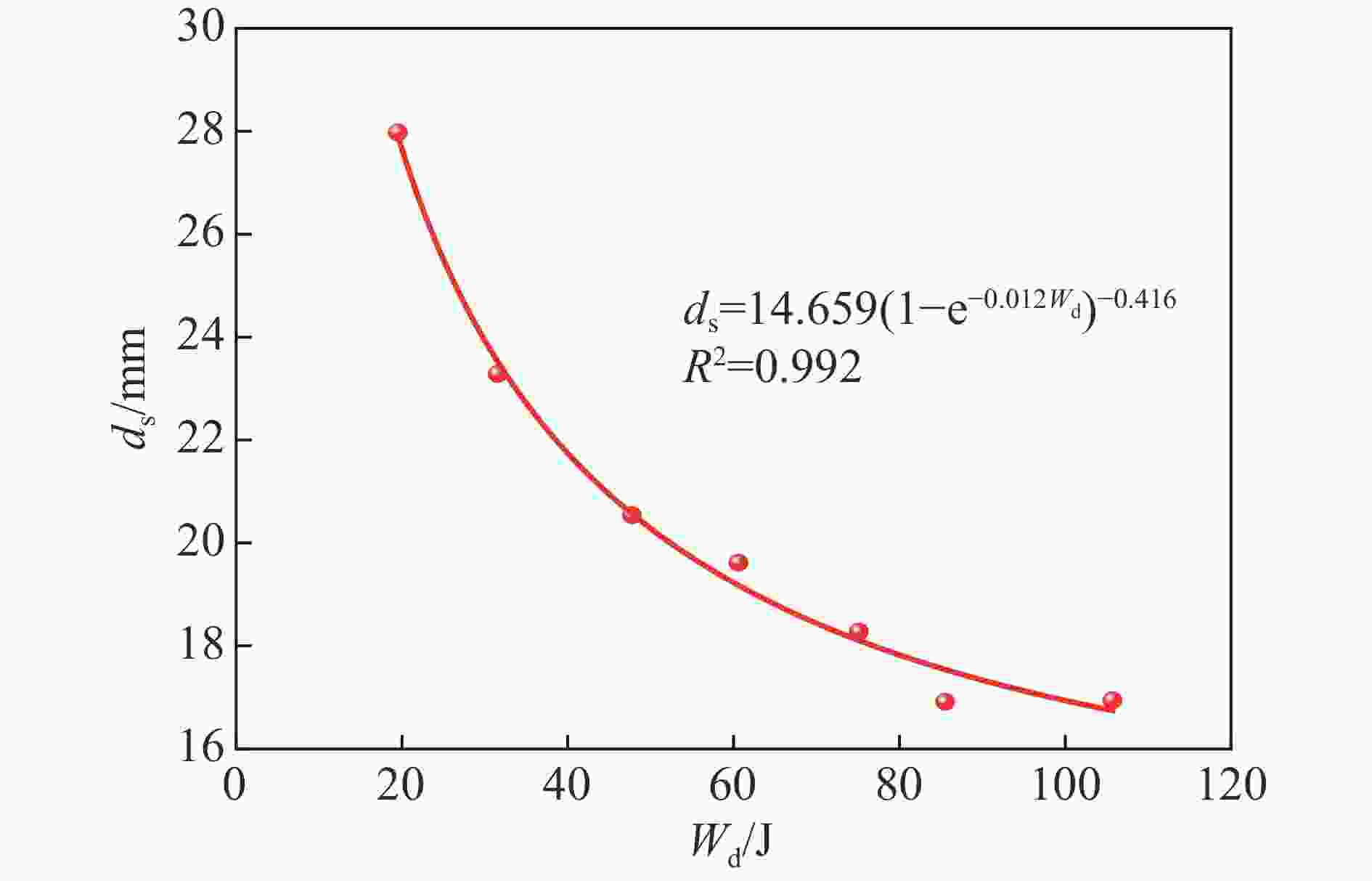
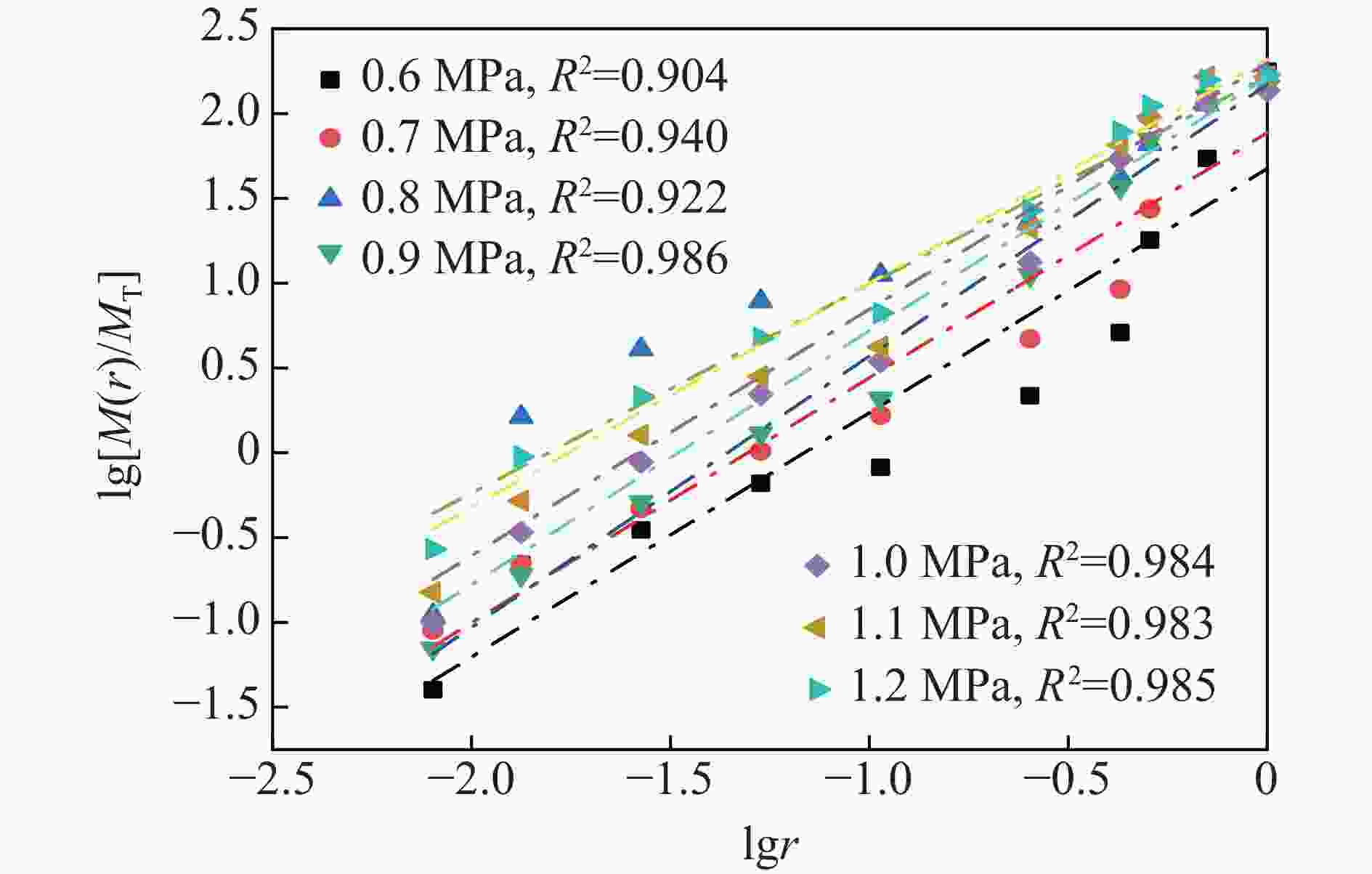
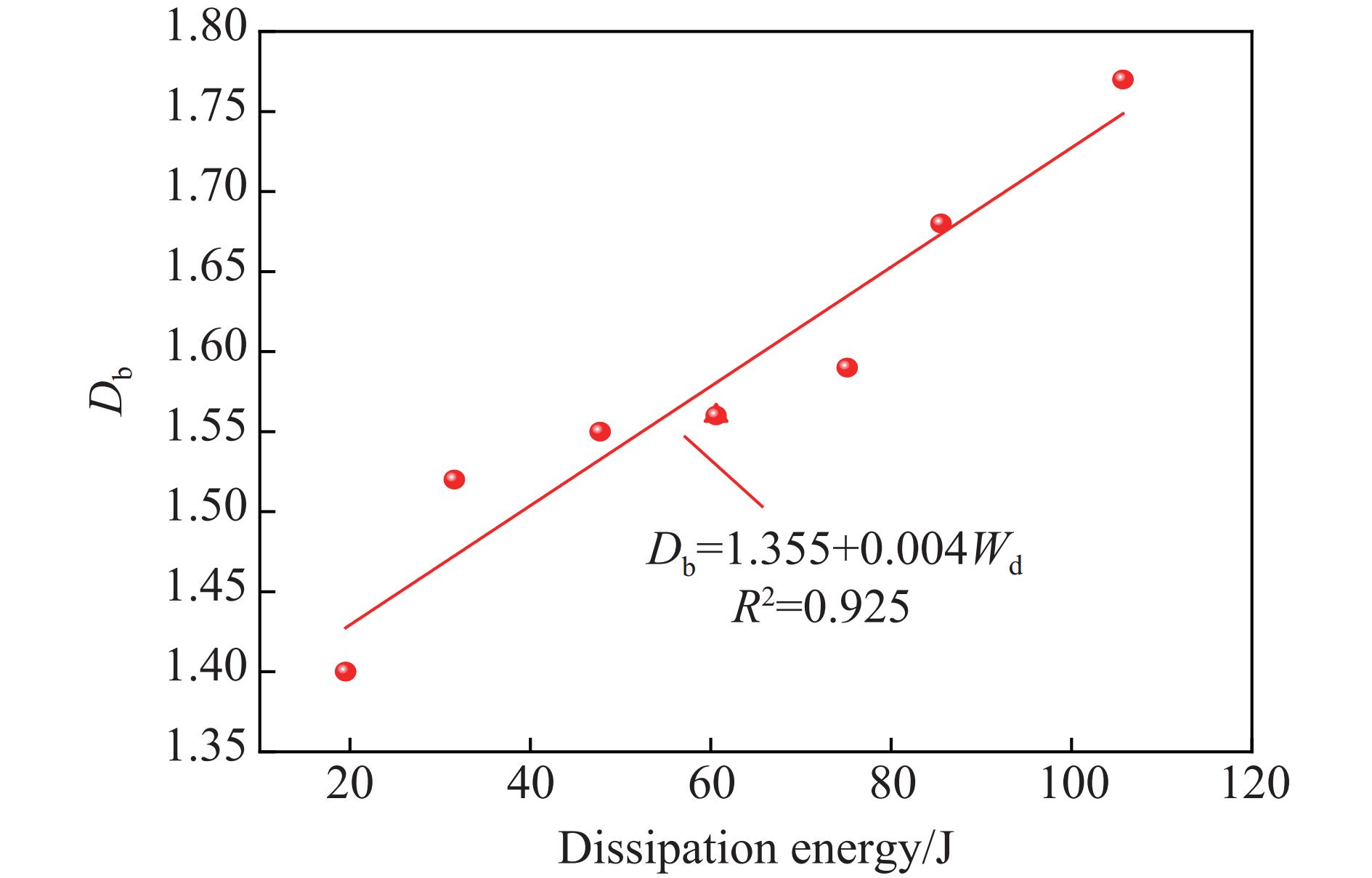
摘要: 为了研究冲击荷载作用下含铜矿岩的破碎块度与能量耗散关系，借助分离式霍普金森压杆试验装置，分析不同冲击荷载下含铜凝灰岩的力学特性及能量传递规律，结合分形理论构建耗散能与矿岩破碎块度之间的关系；同时，基于有限离散元方法（finite discrete element method，FDEM）模拟矿岩的裂纹扩展行为。结果表明：随着入射能的增加，透射能、耗散能、反射能三者的能量分布规律基本保持一致，即透射能、耗散能、反射能依次减小；根据耗散能的不同，碎石块度分布也呈现出明显的差异性。当耗散能由19.52 J增加至105.72 J时，矿岩的平均块度从27.98 mm降低至16.94 mm，分形维数提升了26.43%，表明耗散能越高，矿岩的宏观破碎程度越剧烈，破碎块度的数目越多，碎块粒径越小，均匀性越好；随着冲击荷载的增大，裂纹起裂时间缩短，拉伸裂纹数量占总裂纹数量的比重提高。FDEM数值计算方法的应用可为深入解析岩石断裂破坏特性提供新的思路。Abstract: To understand the relationship between fragmentation and energy dissipation in copper-bearing ore rock subjected to impact loading, a split Hopkinson pressure bar (SHPB) testing apparatus was employed to study the mechanical properties and energy transfer mechanisms of copper-bearing tuff under varying impact loads. Additionally, fractal theory was used to establish the correlation between dissipated energy and rock fragmentation. Utilizing the finite discrete element method (FDEM), numerical simulations of crack propagation within the rock were conducted. The results indicate that as the incident energy increases, the distribution patterns of the transmission energy, absorbed energy and reflection energy remain consistent, which are characterized by transmission energy, absorbed energy and reflection energy decreased successively. Furthermore, significant variations in fragment size distribution are observed with changes in dissipated energy. Specifically, as dissipated energy increases from 19.52 J to 105.72 J, the average fragment size decreases from 27.98 mm to 16.94 mm, while the fractal dimension increases by 26.43%. This suggests that higher dissipated energy results in more extensive macroscopic fragmentation, an increase in the number of fragments, smaller particle sizes and enhanced uniformity. As the impact load intensifies, the time to crack initiation decreases, and the proportion of tensile cracks relative to total cracks increases. The application of the FDEM offers new insights into the fracture and failure characteristics of rocks.
-
铜作为生产生活中应用最广泛的金属之一，在国民经济建设中发挥着重要作用[1]。为了获取金属铜，首先需对含铜矿岩实施爆破，然后对所采矿岩进行二次爆破或机械压碎、磨碎等碎矿过程，以减小矿岩块度。在运用爆破、机械等手段破碎矿岩时，往往存在能量利用率低、耗散大等的问题。随着国家对矿产资源绿色开发战略的实施，矿山企业常常面临节能降耗的艰巨任务，因此，减少矿岩破碎过程中能量消耗的问题亟待解决。
在矿山开采过程中，动载破碎仍为破岩的主流方法，当前用于研究岩石动态力学特性的设备主要有落锤、轻型气炮、飞片及分离式霍普金森压杆（split Hopkinson pressure bar，SHPB）等，其中应用最广泛的为SHPB装置。目前，学者们已经针对岩石破碎过程中的能耗特征与块度分布开展了一系列的研究与探讨，并取得了一定的成果。黎立云等[2]采用SHPB开展了砂岩的动态冲击试验，通过调整冲击气压，获得了不同应变率下砂岩试件的破坏模式。武仁杰等[3]通过对层状岩石进行SHPB试验，研究了不同层理倾角的层状岩石在不同冲击速度荷载下岩石破碎块度与各能量间的关系。Cho等[4]对花岗岩和凝灰岩开展了不同冲击气压的动态压缩试验，发现2种岩石材料的动态抗压强度均与平均应变率呈明显的正相关关系。江益辉[5]采用异形冲头SHPB试验系统，同时借助高速摄影机，探究了花岗岩超过峰值应力后的损伤破坏特征，此外，建立了PFC2D数值模型，进一步从理论角度解释了花岗岩在峰后损伤破坏的机制机理。尤业超等[6]基于能量原理分析了三轴压力下盐岩的能量传递规律及破坏模式。Ping等[7]对砂岩开展了一系列的动态劈裂试验，分别探讨了25～800 °C热处理后砂岩的动态拉伸特性。Li等[8]利用自主改进的SHPB系统，探究了在三维压力条件下盐岩的动态力学特性，并定量分析了盐岩在破碎过程中各能量的传递规律。Yu等[9]采用SHPB系统对大理岩进行了动态三点弯曲试验，结果表明，随着大理岩试件动态累积损伤的增加，其动态断裂韧性与断裂能均逐渐降低。近年来，数值模拟成为研究岩石破裂过程必不可少的手段，利用有限离散元方法（finite discrete element method, FDEM）模拟岩石的连续-非连续断裂过程受到越来越多学者的关注[10-12]。
综上可知，目前的研究大部分针对砂岩、花岗岩、大理岩等单一岩样，对于含金属矿物成分的矿岩动态力学特性研究较少。为此，本文中，借助SHPB对含铜凝灰岩进行常规冲击试验，基于应力波传播理论、能量守恒定律、分形维数理论和FDEM方法，研究含铜凝灰岩在冲击荷载作用下的能量耗散和裂纹扩展行为，以期为降低采选过程中的能量消耗提供理论参考。
1. 冲击试验设备及试件制作
1.1 试验设备
选择昆明理工大学
∅ 50 mm分离式霍普金森杆进行常规冲击试验，如图1所示。试验设备中的弹性压杆均由Cr40合金钢加工而成，密度为7 800 kg/m3，弹性模量为210 GPa，纵波波速为5 190 m/s，其中入射杆和透射杆长均为2 m，纺锤形子弹冲头长为0.4 m。基于一维应力波假设和应力均匀性假定[13-15]，采用“三波法”将存储的试验数据进行分析处理，便可得到试件在冲击压缩过程中的动态应力
σs(t) 、应变率˙ε(t) 以及轴向应变ε(t) ：σs(t)=Ae2As[σi(t)+σr(t)+σt(t)] (1) ˙ε(t)=σi(t)+σr(t)−σt(t)ρeceLs (2) ε(t)=1ρeceLs∫t0[σi(t)−σr(t)−σt(t)]dt (3) 式中：
σi(t) 为入射应力，σr(t) 为反射应力，σt(t) 为透射应力，ρece 、ce 、Ls 分别为弹性压杆的波阻抗、纵波波速和试件长度，Ae 、As 分别为弹性压杆和被测试件的横截面积。1.2 试件制作
试验所用试件均取自云南省大红山铜矿某中段，其岩性主要为深灰至灰黑色含铜磁铁纳长凝灰岩，矿体呈顺层条纹条带状、细脉状产出，平均品位为25.67%，主要脉石矿物为钠长石、石榴子石、黑云母、石英。试件表面存在少许点星铜斑，但总体结构单一，质地紧密，岩样加工尺寸符合国际岩石力学学会（ISRM）规定的标准尺寸[16]，直径（D）为50 mm，高（L）为25 mm，加工后的部分试件如图2所示，本文中统称“含铜矿岩”。
为了尽量减少端面效应及弥散效应，需要对含铜矿岩的端面进行仔细打磨，确保端面不平行度和不垂直度均小于0.02 mm，尽量选择密度、纵波波速等参数相近的试件，部分含铜矿岩的基本物理力学参数如表1所示。
表 1 含铜矿岩基本物理力学参数Table 1. Basic physical and mechanical parameters of copper-bearing rock specimen编号 密度/
(g·cm−3)纵波波速/
(m·s−1)弹性模量/
GPa泊松比 抗压强度/
MPaJ-1 3.10 3 549 93.35 0.33 59.23 2. 能量分析
2.1 能量计算依据
根据一维应力波传播理论和能量守恒定律，入射能
Wi 、透射能Wr 、反射能Wt 、耗散能量Wd 可分别表示为：Wi=AsceE0∫t0ε2i(t)dt (4) Wr=AsceE0∫t0ε2r(t)dt (5) Wt=AsceE0∫t0ε2t(t)dt (6) Wd=Wi−Wr−Wt (7) 式中：
εi(t) 、εr(t) 、εt(t) 分别为入射、反射及透射波的应变，E0 为弹性杆的弹性模量。2.2 动态应力平衡分析
试验选用0.5～1.2 MPa区间的冲击气压p，每间隔0.1 MPa为1个等级，共分为8个等级，每级冲击3～5个试件，图3为随机选取的试件B-2（冲击气压为0.6 MPa）的动态加载应力平衡曲线。图中显示了试件入射端与透射端的应力平衡情况，其中，入射应力波与反射应力波叠加形成的曲线与透射应力波曲线基本重叠，表明在整个冲击过程中，矿岩试件左右两端面的应力基本保持一致，符合动态应力平衡，因此，说明试验结果的可靠性较高。
通过式(1)～式(7)，可以得到不同冲击荷载下含铜矿岩的平均应变率、峰值应力、入射能、反射能、透射能及耗散能，筛选出每组典型含铜矿岩的测试数据，具体计算结果如表2所示。
表 2 含铜矿岩的冲击实验数据Table 2. SHPB test data of copper-bearing rock samples编号 冲击气压/
MPa平均应
变率/s−1峰值应力/
MPaWi/J Wr/J Wt/J Wd/J A-3 0.5 30.68 108.03 63.34 7.24 45.13 10.62 B-2 0.6 35.71 119.72 81.67 5.73 55.75 19.51 C-4 0.7 44.25 141.35 105.92 7.32 66.10 31.57 D-1 0.8 50.93 163.19 130.76 8.05 74.19 47.75 E-3 0.9 53.62 189.55 168.28 23.94 83.45 60.60 F-2 1.0 59.15 200.93 203.33 37.88 89.99 75.12 G-4 1.1 64.81 249.80 222.91 43.46 93.01 85.52 H-1 1.2 77.39 265.90 267.09 62.21 99.06 105.72 图4给出了含铜矿岩不同冲击荷载下入射能与冲击气压的关系曲线，入射能与冲击气压之间存在较好的线性关系，拟合关系式为：Wi=293.11p–93.73，相关系数R2=0.989。因此，对含铜矿岩进行冲击加载时，可通过调整冲击气压实现对输入能量的控制。
图 4 冲击气压与入射能曲线关系Figure 4. Relationship between impact pressure and incident energy curve2.3 能量传递规律
分别选取冲击气压为0.5、0.7、0.9和1.1 MPa时的能量时程曲线，如图5所示。从图5可以看出，4种不同的冲击气压下，能量变化随冲击作用时间大致分为3个阶段： 第1阶段，入射、反射、透射及耗散能量从零开始缓慢增长；第2阶段，入射、透射及耗散能量随时间的增长明显增加；第3阶段，各能量曲线发展趋势开始趋缓，随后基本保持恒定；其中反射能量的时程曲线在整个过程近似为一条水平直线。当冲击气压分别为0.5、0.7、0.9和1.1 MPa时，加载持续时间分别为327、295、249和223 μs，能量达到恒定的起始时间分别为184、179、174和181 μs。这表明，随着冲击气压的增加，总的加载时间不断缩短，能量越快达到平衡，冲击气压越大，对含铜矿岩的破碎效率越高。
矿岩在破碎过程中，其本质是能量相互转化的过程，为了进一步探究冲击过程中各能量的传递规律，引入能量比率（反射能、透射能、耗散能分别占入射能的比值）用于描述能量的传递规律[17-18]。
图6给出了含铜矿岩在不同冲击气压下能量反射率、透射率、耗散率与入射能之间的关系，可以发现，随着入射能的增加，3种能量整体的大小关系基本保持一致，即透射能、耗散能、反射能依次减小。当入射能小于110 J时，随着入射能的增加，能量耗散率逐渐增大，透射率逐渐减小，反射率减小；当入射能大于200 J之后，随着入射能的增加，能量耗散率、透射率和反射率的范围分别为39.58%～39.95%、37.09%～44.29%和18.77%～23.32%，表明在冲击过程中，约有60%的入射能被透反射波耗散。同时发现，随着入射能的增长，能量耗散率并无明显变化。
图 6 冲击荷载下含铜矿岩能量比率传递规律Figure 6. Energy ratio transfer of copper bearing rock under impact load3. 含铜矿岩破碎效果
3.1 破碎形态
当矿岩所受到冲击荷载超过了其极限强度，矿岩开始发生破坏，将会形成新的细小的微裂纹，随着荷载的持续，微小裂纹便会进一步扩展、贯通。当耗散能较小时，矿石内部的所能释放的弹性应变能变小，新生裂纹一般沿着轴向加载方向进行贯通，即出现破裂拉伸破坏，过程以张拉应力为主。当耗散能较大时，矿石内部的所释放的弹性应变能较多，新生裂纹的数量也会增加，不同尺寸的裂纹构成了错综复杂的裂隙网络，迅速贯通切割矿岩，此时以张拉应力与剪切应力共同作用。
图7为矿岩在不同耗散能条件下的破坏形态，随着耗散能增加，试件的破坏模式是由轴向劈裂拉伸破坏向整体压碎破坏的方向发展，其中试件碎片体积不断减小，碎块数目明显增多，显示出了矿岩试件破碎与耗散能具有较强的相关性。
图 7 不同耗散能下含铜矿岩的破碎模式Figure 7. Fracture patterns of copper bearing rocks under different dissipated energies3.2 不同耗散能下含铜矿岩累积质量分布
为了能具体量化出矿岩在冲击荷载下，耗散能的变化对矿岩破碎效果的影响，将矿岩碎屑进行收集，选用10个等级标准圆孔筛对矿岩碎屑进行筛分试验，并通过电子秤称取每个标准筛网中矿石碎块的质量，各等级孔径及矿岩碎块质量如表3所示。A-3矿岩试件发生的是拉伸破坏，因此，不进行筛分处置。
表 3 含铜矿岩破碎块度筛分试验结果Table 3. Test screening results of crushed copper-bearing rock fragments编号 Wd/J 各等级粒径岩矿碎块的质量/g 平均块度/
mm<0.3 mm <0.5 mm <1.0 mm <2.0 mm <4.0 mm <9.5 mm <16.0 mm <19.0 mm <26.5 mm <37.5 mm B2-0.6 19.52 0.04 0.18 0.13 0.31 0.16 1.35 2.95 12.8 36.44 123.42 27.98 C4-0.7 31.58 0.09 0.13 0.25 0.55 0.64 3.03 4.50 18.16 91.39 51.51 23.29 D1-0.8 47.75 0.11 1.52 2.46 3.74 3.39 12.10 18.87 24.19 47.12 53.92 20.54 E3-0.9 60.61 0.07 0.12 0.32 0.79 0.78 9.06 25.52 33.49 55.18 20.42 19.62 F2-1 75.13 0.10 0.24 0.54 1.33 1.25 9.85 40.75 39.61 22.46 20.47 18.28 G4-1.1 85.53 0.15 0.37 0.75 1.55 1.38 16.84 44.16 30.27 69.63 0 16.92 H3-1.2 105.72 0.27 0.68 1.20 2.60 1.92 20.17 51.22 32.99 46.95 12.74 16.94 对表3中不同耗散能与矿岩碎块质量分布的数据进行汇总并分析对比，可以得到不同耗散能与矿岩碎块质量分布的关系，如图8所示。根据曲线走势可以看出，所有曲线均包含2个拐点，第1个拐点位于粒径为9 mm左右的区域，第2个拐点出现在粒径为27 mm左右的区域。当粒径位于0～9 mm区域时，筛中累积质量百分比随粒径的增大缓慢增加，当超过第1个拐点但未超过第2个拐点时，曲线加速上升。当超过第2个拐点后，曲线的增长趋势出现了不同程度的减缓，其变化规律与耗散能有关。当耗散能为19.52 J时，矿岩试件破碎后存在明显的大块，矿岩碎块粒径分布以大于37.5 mm为主，其质量约占整体的70%。当耗散能为31.58 J时，矿岩碎块粒径主要集中分布于19.0～26.5 mm区域内，其质量占总体的50%左右，当耗散能超过100 J后，随着耗散能的增大，矿岩碎块的数目明显增多，但几乎无明显大块出现，矿岩碎块粒径为9.5～26.5 mm的矿岩质量约占总体质量的88%，综合分析可知，随着耗散能的增加，矿岩破坏后的碎块粒径变化主要由粗粒端向细粒端发展。
图 8 不同耗散能与含铜矿岩破碎块度分布Figure 8. Mass distribution against fragment size for different absorbed energy by copper bearing rocks3.3 平均块度分析
平均块度与能量耗散关系密切[19-20]，用矿岩破碎的平均块度ds对破碎程度进行表征：
ds=∑ridi/∑ri (8) 式中：
di 为不同等级筛网的粒径，ri 为筛分粒径为Ri时所对应的碎块质量百分比。图9给出了耗散能与矿岩破碎块度平均尺寸之间的关系，由图9可知，随着耗散能的增加，矿岩破碎的平均块度呈幂指函数降低，当耗散能从19.52 J提升至105.72 J时，矿岩破碎的平均块度从27.98 mm降低至16.94 mm，降幅高达40%左右。其主要原因是，随着耗散能的升高，矿岩试件新生裂纹的数量不断增多，众多裂纹之间相互贯通，极易形成宏观破坏面，同时由于整个冲击过程时间较短，应力波传播速度远超过矿岩试件内部裂纹、裂隙的扩展速度，应力波所携带的绝大部分能量将不会沿着试件的裂隙节理进行逸散，则只能以增大矿岩碎块体表面积的方式对能量进行耗散，因此，矿岩破碎数目逐渐增多，其平均块度逐渐降低。
图 9 不同耗散能与矿岩破碎块度的分布Figure 9. Distribution of copper-bearing rock fragmentation for different dissipated energies3.4 矿岩耗散能与分形维数分析
研究发现，矿岩内部的原始缺陷（孔隙、裂隙、节理等）的分布与损伤破坏的演化之间表现出较高的统计自相似性，在冲击荷载下，岩石内部的原始缺陷被迅速激发、活化，裂纹开始发育扩展，甚至交汇贯通，最终导致岩石发生破碎，岩石碎块的块度尺寸与数量差异较大，表现出较大的随机性。为了能较好地描述岩石破碎过程中产生碎块的随机性，本文中借助分形理论对矿岩破碎的随机分布展开研究，进而从随机事件中探明可能存在的某些变化规律。根据（G-G-S）分布函数模型[21-22]，建立含铜矿岩受单轴冲击破碎后的质量-频率分布关系：
y=M(x)MT=(xxm)3−Db (9) 式中：
M(x) 为粒径小于x 的碎块累积质量，MT 为碎块总质量，x 为碎块的粒径，xm 为碎块最大粒径，Db 为矿岩碎块分布分形维数。对式(9)左右两端同时去对数，化简可得：
lgy=lgM(x)MT=(3−Db)lgxxm (10) 根据式(10)可知，利用
lg[M(r)/MT] -lgr 拟合直线中的斜率可求得冲击荷载下含铜矿岩破碎块度的分形维数。图10给出了含铜矿岩破碎块度分形维数计算的双对数关系曲线，由图10可以看出，拟合曲线的线性相关系数R2均在0.9以上，说明在冲击荷载下岩石破碎块度的分布遵循统计意义上的自相似性。当矿岩试件受到高速冲击荷载后，其内部的微缺陷开始延伸、扩展，最终导致试件发生宏观破坏，通常利用碎块的分形表征岩石在冲击荷载下破碎的形成过程[23-24]。基于矿岩碎块的分形特点，可根据不同等级的碎矿要求，选择适当的冲击能量，使矿岩碎块分布范围更均匀，以期达到最佳的破碎效果。
图 10 不同耗散能条件下典型lg[M(r)/MT]-lgr关系曲线Figure 10. Typical lg[M(r)/MT]-lgr curves under different dissipated energies根据典型的
lg[M(r)/MT] -lgr 关系曲线，得出含铜矿岩的块度分形维数，绘制出含铜矿岩在单轴冲击条件下的不同耗散能与块度分形维数的关系，如图11所示。从图11可以明显看出，随着耗散能的升高，分形维数有所增大，呈较强线性关系，其具体拟合关系为：Db=1.35+0.004Wd。耗散能由19.52 J升高至105.72 J时，含铜矿岩的块度分形维数由1.40增至1.77，提高了26.42%。从岩石试件的破坏模式出发，对比图7与9发现，随着耗散能的增加，分形维数明显增大，破碎程度越严重，碎块数目越多，粒径也越小，碎石块度越均匀，表明分形维数在一定范围内可以合理地表征单轴冲击荷载作用下含铜矿岩的宏观破碎程度。
图 11 耗散能与分形维数关系曲线Figure 11. Relationship between fractal dimension and dissipated energy4. FDEM数值计算
4.1 FDEM方法介绍
自从Munjiza提出有限离散元方法后，该方法已被广泛应用于岩土工程与地质工程[25-26]领域。Yan等[27]通过在FDEM中引入一种动态插入内聚元单元算法，提出了一种自适应有限离散元方法，并开发了一种新的内聚元单元本构模型。本文中运用Yan等[28-30]开发的MultiFracs软件进行不同冲击气压下含铜凝灰矿岩在冲击荷载下的断裂破坏数值仿真。
4.1.1 FDEM基本原理
FDEM基本原理是在连续介质中用三角形单元进行划分，同时在相邻三角形单元边缘插入无厚度的节理单元，每个三角单元不共享节点，如图12(a)所示。通过判断节理单元是否断裂，模拟连续体中裂纹的萌生、发育和扩展[31-33]。由于自适应有限离散元方法无需内聚单元模拟连续体变形过程，因此可以提高计算精度。与传统FDEM相比，自适应有限离散元方法可大大缩短计算时间，有效降低计算成本[34-37]。
4.1.2 节理单元断裂本构关系
FDEM中节理单元断裂本构是采用内聚力单元来模拟连续体的破裂过程，避免了破裂过程中质量不守恒和能量的异常损失。该方法采用损伤本构模型表征内聚单元的峰后软化行为。如图12(b)所示。节点本构模型破坏类型一共有3种：拉伸破坏（模型Ⅰ）、剪切破坏（模型Ⅱ）和拉伸-剪切混合破坏（模型Ⅲ）。关于FDEM中节理本构模型详细介绍可参考文献[38-39]。
4.2 参数校准与模型建立
4.2.1 微观参数的选择
对于FDEM方法而言，其输入的物理力学参数均可以从实验中获取，使得宏观参数与微观参数相对应，因此，只需标定裂纹能量释放率（GI和GⅡ）。选取FDEM参数如表4[40]所示，表中：ρ为密度，E为弹性模量，pn为法向接触罚值，pt为切向接触罚值，μ为泊松比，c为黏聚力，ft为抗拉强度，ϕ为内摩擦角，GI为Ⅰ型断裂能，GⅡ为Ⅱ型断裂能，pf为节理罚值。其中，密度、弹性模量、泊松比、抗拉强度、黏聚力、内摩擦角等基础力学参数根据室内试验获取。参考Zuo等[40]的研究成果，三角形单元的法向和切向罚参数设为E，节理单元的法向和切向罚参数设为100E，模拟结果较好。Ⅰ型断裂能GI和Ⅱ型断裂能GⅡ分别为节理单元发生拉伸破坏和剪切破坏时的断裂能量释放率。数值计算软件采用基于FDEM开发的MultiFracs软件进行计算。
三角形单元 节理单元 ρ/(kg·m−3) E/GPa pn/GPa pt/GPa μ c/MPa ft/MPa ϕ/(°) GI/(J·m−2) GII/(J·m−2) pf/GPa 3080 65.00 65.00 65.00 0.28 5.26 8.26 30 1100 2200 6500 4.2.2 模型的建立
采用gmsh软件建立凝灰岩冲击破坏模型，模拟不同冲击荷载下含铜凝灰矿岩的动态响应及断裂破坏过程。数值模拟杆件尺寸与实验室设备尺寸相同，具体模型及网格设置如图13所示，其中入射杆和透射杆长度均为2 m，试件长度和直径均为50 mm，网格总数为20 000。试件采用加密网格进行细化，便于捕捉岩石破碎特征和裂纹扩展，杆件采用更大的网格尺寸来提高计算效率降低计算时间成本。应力加载方式采用纺锤形子弹冲击入射杆进行加载。
4.3 数值计算结果
4.3.1 破裂形态
图14为数值模拟得到的不同冲击气压下矿岩的冲击破坏过程。根据结果可知，随着冲击气压的增大，裂纹起裂步长逐渐减小。以1.2 MPa为例，当应力波从入射杆传到试件中时，在试件首先发生局部拉伸剪切破坏，随着应力波的传播试件裂纹数量继续增加，伴随少量张拉裂纹的生成，此时试件裂纹数量呈稳定增长趋势，此时试件中张拉裂纹并没有急速扩张；当透射端出现透射波和反射波时，试件表现出卸载作用，在此阶段，试件中部迅速多条张拉裂纹，并以显著的速度向透射杆端延展，裂纹数量进入快速上升阶段，其间裂纹宽度明显增大。当张拉裂纹在整个试件贯通后，整体应力水平逐渐降低，裂纹进入缓慢扩展阶段。尽管裂纹宽度持续增大，裂纹数量却基本保持稳定，仅在原有裂纹周边出现局部延伸。最终，裂纹增长停止，意味着试件破坏过程结束。
图 14 不同冲击气压下含铜凝灰矿岩的裂纹演变图（蓝色代表拉伸裂纹，红色代表剪切裂纹）Figure 14. Crack evolution diagram of copper-bearing Tuff specimens under different impact air pressures (blue represents tensile cracks, and red represents shear cracks)4.3.2 裂纹演化特征
图15(a)显示了不同冲击气压下凝灰岩试件裂纹数量演化过程。岩石破裂后，随着应力波的传播，裂纹数量迅速增加，然后生长速度逐渐减慢，直到全部破碎后裂纹停止发育。以1.20 MPa冲击气压裂纹演化过程为例，微裂纹在约50 μs开始萌生，其拉伸裂纹数占比最大，说明裂纹类型以拉伸为主。在随后的裂纹发育期间，剪切裂纹数量逐渐增加，但是裂纹类型仍以拉伸为主。约60 μs后，由于岩石已完全破碎，裂纹数量没有继续增加，保持不变。由图15(a)可知，3类裂纹的演变特征相似，均可分为开始发育、迅速增加、生长缓慢、逐步稳定4个阶段。从图15(b)可知，不同冲击气压岩样拉伸裂纹数量占总裂纹数量之比的平均值为62.30%，表明凝灰岩试件破裂过程中拉伸破坏始终占据主导作用，伴随着应力波的加载发生复杂的拉剪破坏。
5. 结 论
借助SHPB对含铜矿岩进行了常规单轴冲击试验，对比分析了不同冲击荷载作用下含铜矿岩块度分布规律，探讨了不同耗散能对矿岩碎块分布的影响，利用FDEM数值计算方法再现裂纹扩展行为，得出如下主要结论。
(1) 在含铜矿岩SHPB冲击试验中，入射能主要受冲击气压的控制，随着入射能的增加，其他3种能量的分布规律基本保持一致，即透射能、耗散能、反射能依次减小。当入射能低于110 J时，能量耗散率逐渐增大，透射率、反射率逐渐减小，当入射能超过200 J后，各能量比率变化不明显。
(2) 含铜矿岩在不同耗散能的条件下，其破坏形式也存在一定的差异，当耗散能较小时，含铜矿岩以轴向劈裂拉伸破坏为主，随着耗散能逐步增大，矿岩碎块粒径不断减小，表现出由粗粒端向细粒端聚集的趋势。随着耗散能的不断增加，矿岩破碎的平均块度呈幂指函数降低，耗散能由19.52 J提升至105.72 J时，矿岩破碎的平均块度从27.98 mm降低至16.94 mm，下降了39.4%。
(3) 通过FDEM模拟试件的断裂过程，随着冲击气压的增大，裂纹起裂时间逐渐缩短。当冲击气压达到1.2 MPa时，裂纹在约50 μs开始生成，拉伸裂纹数占比达到最大，平均值为62.30%，表明拉伸破坏在整个过程中始终占据主导作用。
(4) 含铜矿石试件破碎块度的分形维数随耗散能的增加呈线性增长，矿岩宏观破碎程度加剧，粒径不断减小，破碎块度的数目明显增多，均匀性越好，当耗散能从19.52 J增至105.72 J时，含铜矿岩破碎块度的分形维数Db提升了26.43%。
-
图 4 冲击气压与入射能曲线关系
Figure 4. Relationship between impact pressure and incident energy curve
图 6 冲击荷载下含铜矿岩能量比率传递规律
Figure 6. Energy ratio transfer of copper bearing rock under impact load
图 7 不同耗散能下含铜矿岩的破碎模式
Figure 7. Fracture patterns of copper bearing rocks under different dissipated energies
图 8 不同耗散能与含铜矿岩破碎块度分布
Figure 8. Mass distribution against fragment size for different absorbed energy by copper bearing rocks
图 9 不同耗散能与矿岩破碎块度的分布
Figure 9. Distribution of copper-bearing rock fragmentation for different dissipated energies
图 10 不同耗散能条件下典型lg[M(r)/MT]-lgr关系曲线
Figure 10. Typical lg[M(r)/MT]-lgr curves under different dissipated energies
图 11 耗散能与分形维数关系曲线
Figure 11. Relationship between fractal dimension and dissipated energy
图 14 不同冲击气压下含铜凝灰矿岩的裂纹演变图（蓝色代表拉伸裂纹，红色代表剪切裂纹）
Figure 14. Crack evolution diagram of copper-bearing Tuff specimens under different impact air pressures (blue represents tensile cracks, and red represents shear cracks)
表 1 含铜矿岩基本物理力学参数
Table 1. Basic physical and mechanical parameters of copper-bearing rock specimen
编号 密度/
(g·cm−3)纵波波速/
(m·s−1)弹性模量/
GPa泊松比 抗压强度/
MPaJ-1 3.10 3 549 93.35 0.33 59.23 
下载: 导出CSV
表 2 含铜矿岩的冲击实验数据
Table 2. SHPB test data of copper-bearing rock samples
编号 冲击气压/
MPa平均应
变率/s−1峰值应力/
MPaWi/J Wr/J Wt/J Wd/J A-3 0.5 30.68 108.03 63.34 7.24 45.13 10.62 B-2 0.6 35.71 119.72 81.67 5.73 55.75 19.51 C-4 0.7 44.25 141.35 105.92 7.32 66.10 31.57 D-1 0.8 50.93 163.19 130.76 8.05 74.19 47.75 E-3 0.9 53.62 189.55 168.28 23.94 83.45 60.60 F-2 1.0 59.15 200.93 203.33 37.88 89.99 75.12 G-4 1.1 64.81 249.80 222.91 43.46 93.01 85.52 H-1 1.2 77.39 265.90 267.09 62.21 99.06 105.72
下载: 导出CSV
表 3 含铜矿岩破碎块度筛分试验结果
Table 3. Test screening results of crushed copper-bearing rock fragments
编号 Wd/J 各等级粒径岩矿碎块的质量/g 平均块度/
mm<0.3 mm <0.5 mm <1.0 mm <2.0 mm <4.0 mm <9.5 mm <16.0 mm <19.0 mm <26.5 mm <37.5 mm B2-0.6 19.52 0.04 0.18 0.13 0.31 0.16 1.35 2.95 12.8 36.44 123.42 27.98 C4-0.7 31.58 0.09 0.13 0.25 0.55 0.64 3.03 4.50 18.16 91.39 51.51 23.29 D1-0.8 47.75 0.11 1.52 2.46 3.74 3.39 12.10 18.87 24.19 47.12 53.92 20.54 E3-0.9 60.61 0.07 0.12 0.32 0.79 0.78 9.06 25.52 33.49 55.18 20.42 19.62 F2-1 75.13 0.10 0.24 0.54 1.33 1.25 9.85 40.75 39.61 22.46 20.47 18.28 G4-1.1 85.53 0.15 0.37 0.75 1.55 1.38 16.84 44.16 30.27 69.63 0 16.92 H3-1.2 105.72 0.27 0.68 1.20 2.60 1.92 20.17 51.22 32.99 46.95 12.74 16.94
下载: 导出CSV
-
[1] 李鹏远, 周平, 唐金荣, 等. 中国铜矿资源供应风险识别与评价: 基于长周期历史数据分析预测法 [J]. 中国矿业, 2019, 28(7): 44–51. DOI: 10.12075/j.issn.1004-4051.2019.07.027.LI P Y, ZHOU P, TANG J R, et al. Identification and evaluation of copper supply risk for China: using method of long-term historical data analysis [J]. China Mining Magazine, 2019, 28(7): 44–51. DOI: 10.12075/j.issn.1004-4051.2019.07.027. [2] 黎立云, 谢和平, 鞠杨, 等. 岩石可释放应变能及耗散能的实验研究 [J]. 工程力学, 2011, 28(3): 35–40. DOI: 10.6052/j.issn.1000-4750.2009.08.0584.LI L Y, XIE H P, JU Y, et al. Experimental investigations of releasable energy and dissipative energy within rock [J]. Engineering Mechanics, 2011, 28(3): 35–40. DOI: 10.6052/j.issn.1000-4750.2009.08.0584. [3] 武仁杰, 李海波. SHPB冲击作用下层状千枚岩多尺度破坏机理研究 [J]. 爆炸与冲击, 2019, 39(8): 083106. DOI: 10.11883/bzycj-2019-0187.WU R J, LI H B. Multi-scale failure mechanism analysis of layered phyllite subject to impact loading [J]. Explosion and Shock Waves, 2019, 39(8): 083106. DOI: 10.11883/bzycj-2019-0187. [4] CHO S H, OGATA Y, KANEKO K. Strain-rate dependency of the dynamic tensile strength of rock [J]. International Journal of Rock Mechanics and Mining Sciences, 2003, 40(5): 763–777. DOI: 10.1016/S1365-1609(03)00072-8. [5] 江益辉. 冲击荷载作用下岩石峰后损伤破坏特性研究 [D]. 长沙: 中南大学, 2014: 48–53.JIANG Y H. Study on post failure behaviors of rock under impact loading [D]. Changsha: Central South University, 2014: 48–53. [6] 尤业超, 李二兵, 谭跃虎, 等. 基于能量耗散原理的盐岩动力特性及破坏特征分析 [J]. 岩石力学与工程学报, 2017, 36(4): 843–851. DOI: 10.13722/j.cnki.jrme.2016.0503.YOU Y C, LI E B, TAN Y H, et al. Analysis on dynamic properties and failure characteristics of salt rock based on energy dissipation principle [J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(4): 843–851. DOI: 10.13722/j.cnki.jrme.2016.0503. [7] PING Q, WU M J, YUAN P, et al. Dynamic splitting experimental study on sandstone at actual high temperatures under different loading rates [J]. Shock and Vibration, 2020, 2020: 8867102. DOI: 10.1155/2020/8867102. [8] LI E B, GAO L, JIANG X Q, et al. Analysis of dynamic compression property and energy dissipation of salt rock under three-dimensional pressure [J]. Environmental Earth Sciences, 2019, 78(14): 388. DOI: 10.1007/s12665-019-8389-7. [9] YU L Y, FU A Q, YIN Q, et al. Dynamic fracturing properties of marble after being subjected to multiple impact loadings [J]. Engineering Fracture Mechanics, 2020, 230: 106988. DOI: 10.1016/j.engfracmech.2020.106988. [10] WU Z J, CUI W J, FAN L F, et al. Mesomechanism of the dynamic tensile fracture and fragmentation behaviour of concrete with heterogeneous mesostructure [J]. Construction and Building Materials, 2019, 217: 573–591. DOI: 10.1016/j.conbuildmat.2019.05.094. [11] FUKUDA D, MOHAMMADNEJAD M, LIU H Y, et al. Development of a 3D hybrid finite-discrete element simulator based on GPGPU-parallelized computation for modelling rock fracturing under quasi-static and dynamic loading conditions [J]. Rock Mechanics and Rock Engineering, 2020, 53(3): 1079–1112. DOI: 10.1007/s00603-019-01960-z. [12] WU D, LI H B, FUKUDA D, et al. Development of a finite-discrete element method with finite-strain elasto-plasticity and cohesive zone models for simulating the dynamic fracture of rocks [J]. Computers and Geotechnics, 2023, 156: 105271. DOI: 10.1016/j.compgeo.2023.105271. [13] 柴少波, 王昊, 井彦林, 等. 充填节理岩石累积损伤动力压缩特性试验研究 [J]. 岩石力学与工程学报, 2020, 39(10): 2025–2037. DOI: 10.13722/j.cnki.jrme.2020.0310.CHAI S B, WANG H, JING Y L, et al. Experimental study on dynamic compression characteristics of rock with filled joints after cumulative damage [J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(10): 2025–2037. DOI: 10.13722/j.cnki.jrme.2020.0310. [14] 滕骁, 卢玉斌, 陈兴, 等. 再生混凝土动态直接拉伸的试验研究 [J]. 振动与冲击, 2016, 35(9): 43–51. DOI: 10.13465/j.cnki.jvs.2016.09.008.TENG X, LU Y B, CHEN X, et al. Tests for dynamic direct tensile of recycled aggregate concrete [J]. Journal of Vibration and Shock, 2016, 35(9): 43–51. DOI: 10.13465/j.cnki.jvs.2016.09.008. [15] 魏威. 冲击载荷作用下活性材料的响应特性研究 [D]. 北京: 北京理工大学, 2016: 35–39.WEI W. Study on the dynamic responses of the active materialsunder impact loadings [D]. Beijing: Beijing Institute of Technology, 2016: 35–39. [16] 王建国, 雷振, 杨阳, 等. 饱水冻结花岗岩动态力学性状的应变率效应 [J]. 地下空间与工程学报, 2018, 14(5): 1292–1297.WANG J G, LEI Z, YANG Y, et al. Strain rate effect of dynamic mechanical characteristics of saturated freezing granite [J]. Chinese Journal of Underground Space and Engineering, 2018, 14(5): 1292–1297. [17] 袁芝斌. 大红山铜矿深部巷道围岩动态破碎耗能规律研究 [D]. 昆明: 昆明理工大学, 2021: 53–56. DOI: 10.27200/d.cnki.gkmlu.2021.000385.YUAN Z B. Research on the energy dissipation mechanism of dynamic fragmentation in surrounding rock of deep shafts in the Dahongshan copper mine [D]. Kunming: Kunming University of Science and Technology, 2021: 53–56. DOI: 10.27200/d.cnki.gkmlu.2021.000385. [18] 王浩. 大红山铜矿深埋变质灰岩动态响应特征研究 [D]. 昆明: 昆明理工大学, 2021: 68–69. DOI: 10.27200/d.cnki.gkmlu.2021.001943.WANG H. Study on the dynamic response characteristics of deeply buried metamorphic limestone in the Dahongshan copper mine [D]. Kunming: Kunming University of Science and Technology, 2021: 68–69. DOI: 10.27200/d.cnki.gkmlu.2021.001943. [19] 谢和平, 高峰. 岩石类材料损伤演化的分形特征 [J]. 岩石力学与工程学报, 1991, 10(1): 74–82.XIE H P, GAO F. The fractal features of the damage evolution of rock materials [J]. Chinese Journal of Rock Mechanics and Engineering, 1991, 10(1): 74–82. [20] 梁正召, 唐春安, 唐世斌, 等. 岩石损伤破坏过程中分形与逾渗演化特征 [J]. 岩土工程学报, 2007, 29(9): 1386–1391. DOI: 10.3321/j.issn:1000-4548.2007.09.017.LIANG Z Z, TANG C A, TANG S B, et al. Characteristics of fractal and percolation of rocks subjected to uniaxial compression during their failure process [J]. Chinese Journal of Geotechnical Engineering, 2007, 29(9): 1386–1391. DOI: 10.3321/j.issn:1000-4548.2007.09.017. [21] 李祥龙, 何丽华, 栾龙发, 等. 露天煤矿高台阶抛掷爆破爆堆形态模拟 [J]. 煤炭学报, 2011, 36(9): 1457–1462. DOI: 10.13225/j.cnki.jccs.2011.09.014.LI X L, HE L H, LUAN L F, et al. Simulation model for muckpile shape of high bench cast blasting in surface coal mine [J]. Journal of China Coal Society, 2011, 36(9): 1457–1462. DOI: 10.13225/j.cnki.jccs.2011.09.014. [22] 杨军, 王国生. 分形几何在岩石爆破研究中的应用 [J]. 爆破, 1995(4): 1–5. [23] 丁希平, 冯叔瑜, 魏伴云. 硐室爆破法采石级配预测 [J]. 爆炸与冲击, 1997, 17(4): 326–332. DOI: 10.11883/1001-1455(1997)04-0326-7.DING X P, FENG S Y, WEI B Y. Prediction of rock fragment distribution for chamber blasting [J]. Explosion and Shock Waves, 1997, 17(4): 326–332. DOI: 10.11883/1001-1455(1997)04-0326-7. [24] 杨仁树, 李炜煜, 杨国梁, 等. 炸药类型对富铁矿爆破效果影响的试验研究 [J]. 爆炸与冲击, 2020, 40(6): 065201. DOI: 10.11883/bzycj-2019-0396.YANG R S, LI W Y, YANG G L, et al. Experimental study on the blasting effects of rich-iron ore with different explosives [J]. Explosion and Shock Waves, 2020, 40(6): 065201. DOI: 10.11883/bzycj-2019-0396. [25] MUNJIZA A, OWEN D R J, BICANIC N. A combined finite-discrete element method in transient dynamics of fracturing solids [J]. Engineering Computations, 1995, 12(2): 145–174. DOI: 10.1108/02644409510799532. [26] MUNJIZA A. Special issue on the discrete element method: aspects of recent developments in computational mechanics of discontinua [J]. Engineering Computations, 2009, 26(6). DOI: 10.1108/ec.2009.18226faa.001. [27] YAN C Z, ZHENG Y C, WANG G. A 2D adaptive finite-discrete element method for simulating fracture and fragmentation in geomaterials [J]. International Journal of Rock Mechanics and Mining Sciences, 2023, 169: 105439. DOI: 10.1016/j.ijrmms.2023.105439. [28] YAN C Z, LUO Z Q, ZHENG Y C, et al. A 2D discrete moisture diffusion model for simulating desiccation fracturing of soil [J]. Engineering Analysis with Boundary Elements, 2022, 138: 42–64. DOI: 10.1016/j.enganabound.2022.02.006. [29] YAN C Z, WANG T, KE W H, et al. A 2D FDEM-based moisture diffusion-fracture coupling model for simulating soil desiccation cracking [J]. Acta Geotechnica, 2021, 16(8): 2609–2628. DOI: 10.1007/s11440-021-01297-4. [30] YAN C Z, FAN H W, HUANG D R, et al. A 2D mixed fracture-pore seepage model and hydromechanical coupling for fractured porous media [J]. Acta Geotechnica, 2021, 16(10): 3061–3086. DOI: 10.1007/s11440-021-01183-z. [31] OÑATE E, ROJEK J. Combination of discrete element and finite element methods for dynamic analysis of geomechanics problems [J]. Computer Methods in Applied Mechanics and Engineering, 2004, 193(27/28/29): 3087–3128. DOI: 10.1016/j.cma.2003.12.056. [32] YAN C Z, ZHAO Z H, YANG Y, et al. A three-dimensional thermal-hydro-mechanical coupling model for simulation of fracturing driven by multiphysics [J]. Computers and Geotechnics, 2023, 155: 105162. DOI: 10.1016/j.compgeo.2022.105162. [33] YAN C Z, MA H, TANG Z C, et al. A two-dimensional moisture diffusion continuous model for simulating dry shrinkage and cracking of soil [J]. International Journal of Geomechanics, 2022, 22(10): 04022172. DOI: 10.1061/(ASCE)GM.1943-5622.0002570. [34] YAN C Z, ZHENG H, SUN G H, et al. Combined finite-discrete element method for simulation of hydraulic fracturing [J]. Rock Mechanics and Rock Engineering, 2016, 49(4): 1389–1410. DOI: 10.1007/s00603-015-0816-9. [35] LISJAK A, TATONE B S A, MAHABADI O K, et al. Hybrid finite-discrete element simulation of the EDZ formation and mechanical sealing process around a microtunnel in opalinus clay [J]. Rock Mechanics and Rock Engineering, 2016, 49(5): 1849–1873. DOI: 10.1007/s00603-015-0847-2. [36] WANG T, YAN C Z, HAN D, et al. Insights into the breaking mechanism and fragment pattern of soft rock assisted by free face under TBM wedge cutter indentation [J]. Engineering Fracture Mechanics, 2023, 291: 109580. DOI: 10.1016/j.engfracmech.2023.109580. [37] WANG T, YAN C Z, ZHENG H, et al. Optimum spacing and rock breaking efficiency of TBM double disc cutters penetrating in water-soaked mudstone with FDEM [J]. Tunnelling and Underground Space Technology, 2023, 138: 105174. DOI: 10.1016/j.tust.2023.105174. [38] FUKUDA D, NIHEI E, CHO S H, et al. Development of a numerical simulator for 3-D dynamic fracture process analysis of rocks based on hybrid FEM-DEM using extrinsic cohesive zone model [J]. Materials Transactions, 2020, 61(9): 1767–1774. DOI: 10.2320/matertrans.Z-M2020833. [39] DENG P H, LIU Q S, HUANG X, et al. Sensitivity analysis of fracture energies for the combined finite-discrete element method (FDEM) [J]. Engineering Fracture Mechanics, 2021, 251: 107793. DOI: 10.1016/j.engfracmech.2021.107793. [40] ZUO T, LI X L, WANG J G, et al. Insights into natural tuff as a building material: effects of natural joints on fracture fractal characteristics and energy evolution of rocks under impact load [J]. Engineering Failure Analysis, 2024, 163: 108584. DOI: 10.1016/j.engfailanal.2024.108584. -
下载:
计量
- 文章访问数: 276
- HTML全文浏览量: 40
- PDF下载量: 69
- 被引次数: 0