Influence of serrated configuration on transverse overload ofthe projectile penetrating with a small attack angle
-
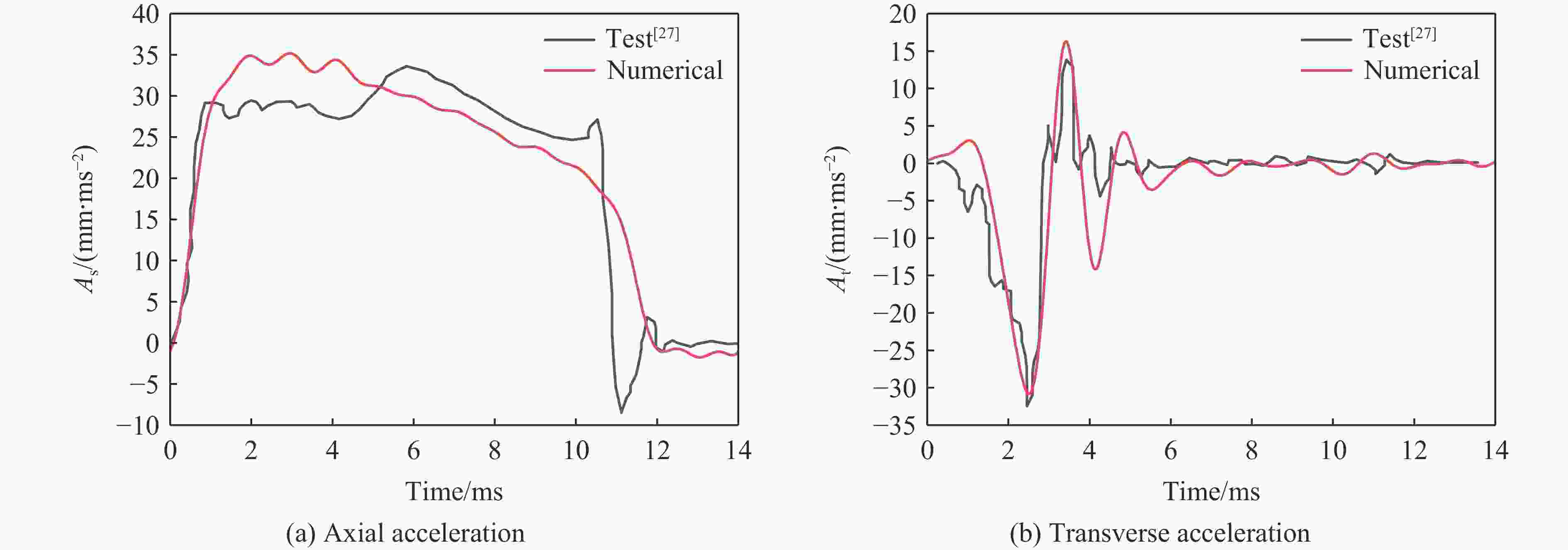
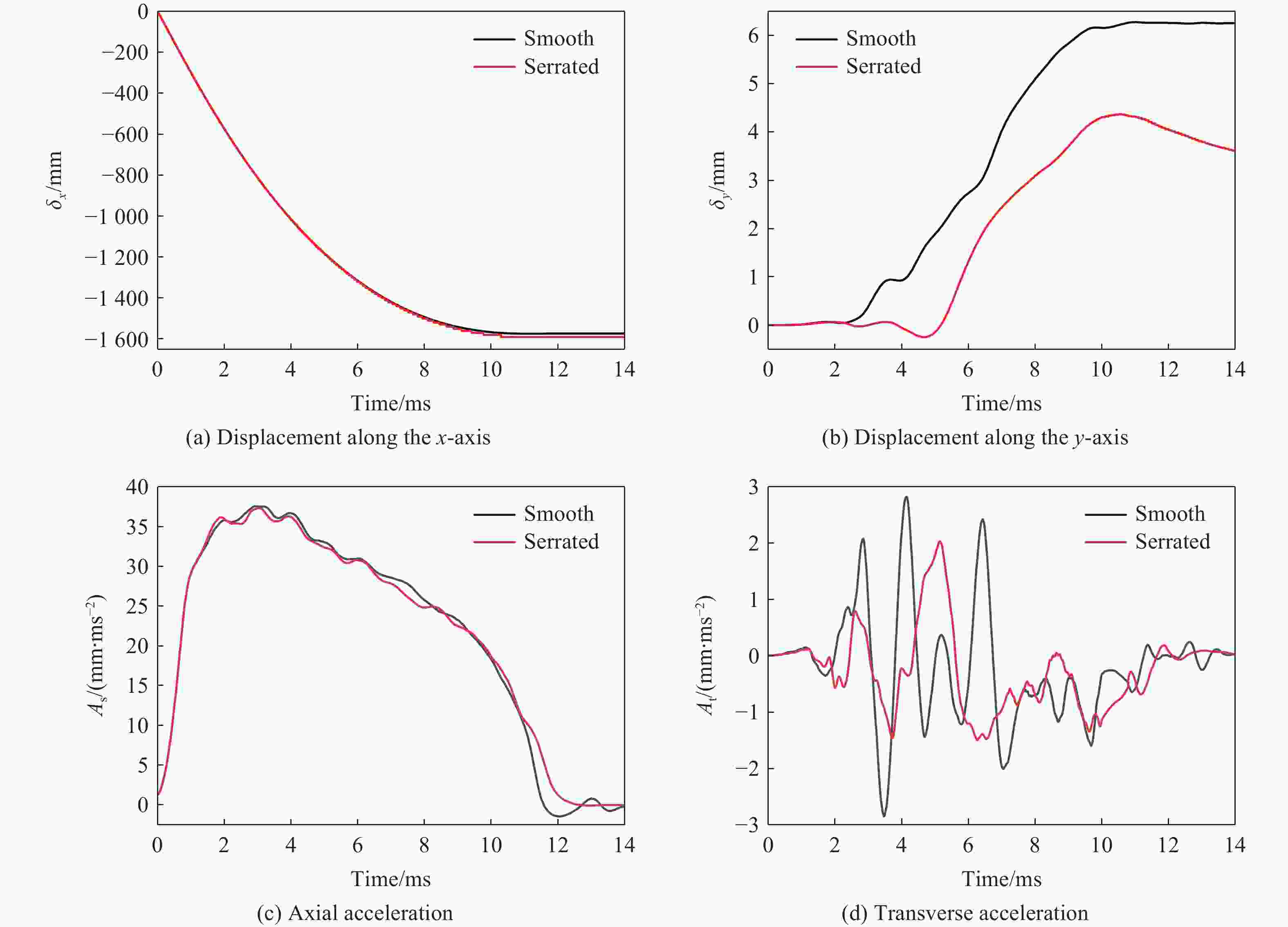
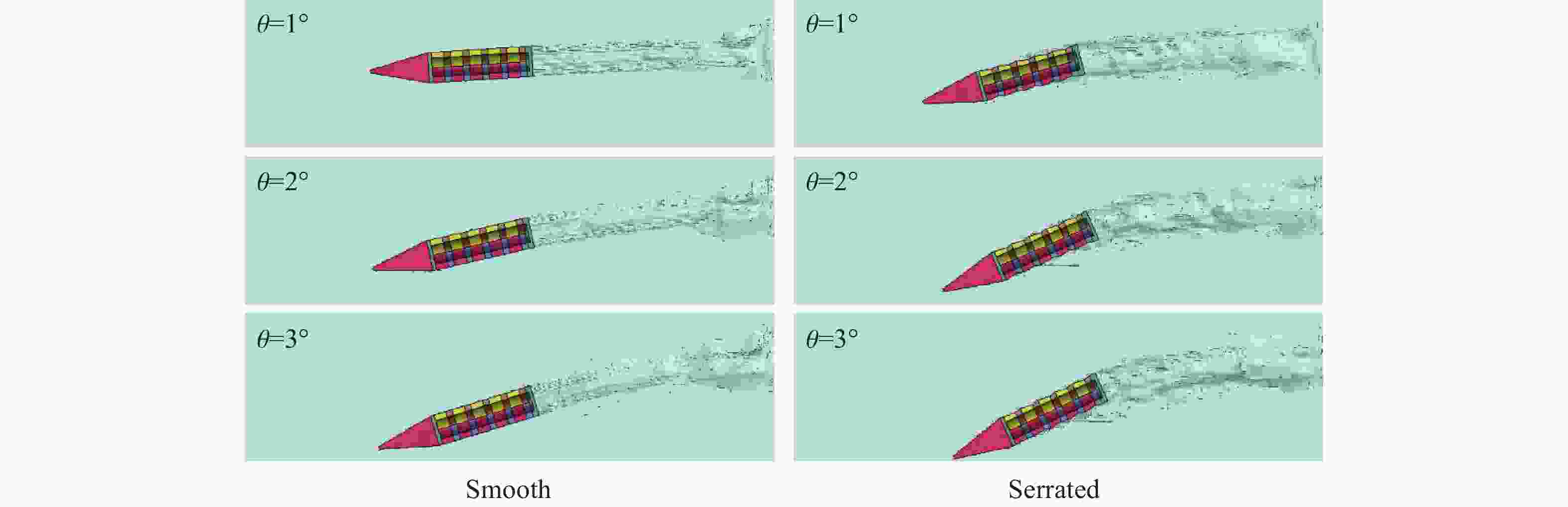
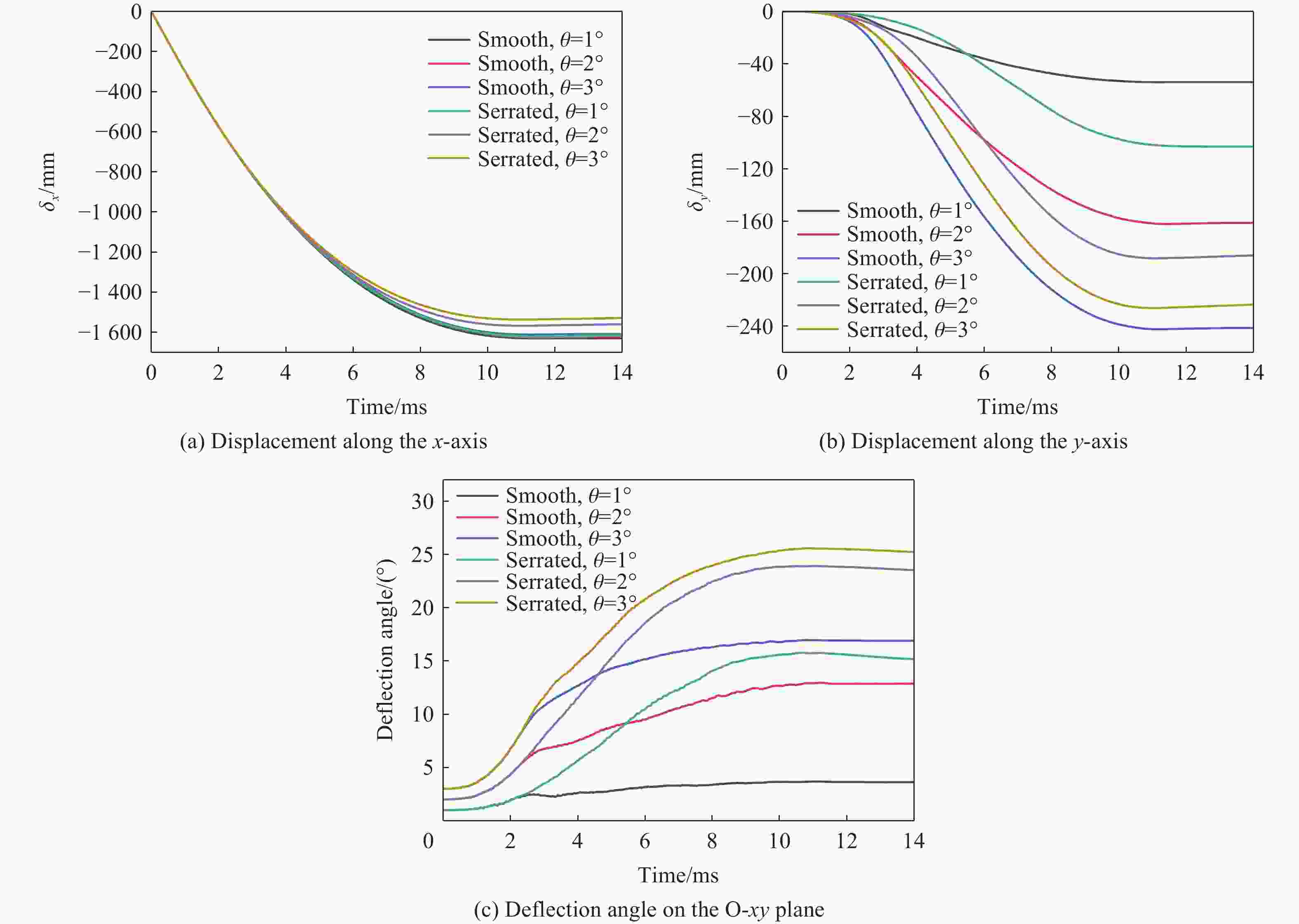
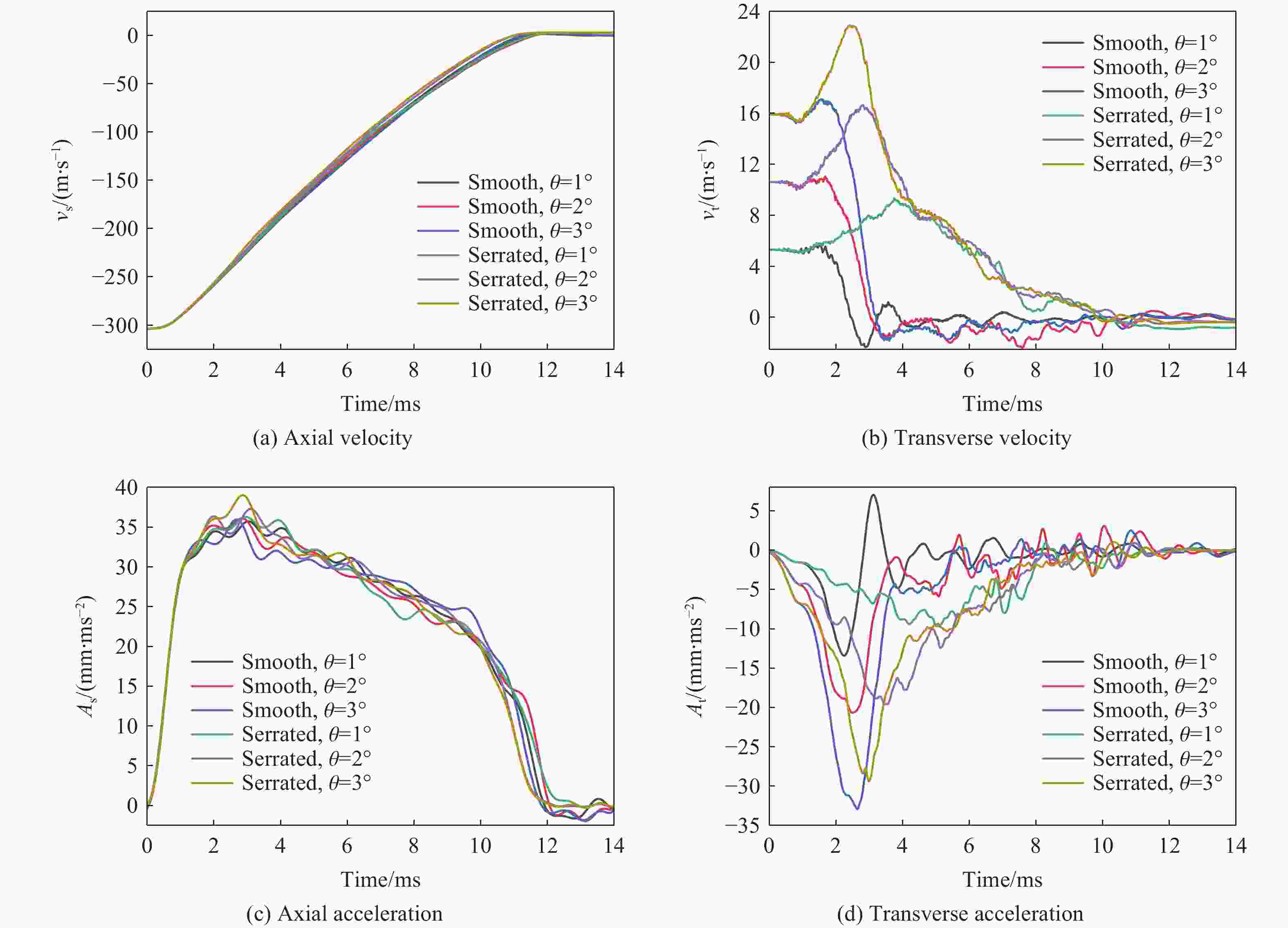
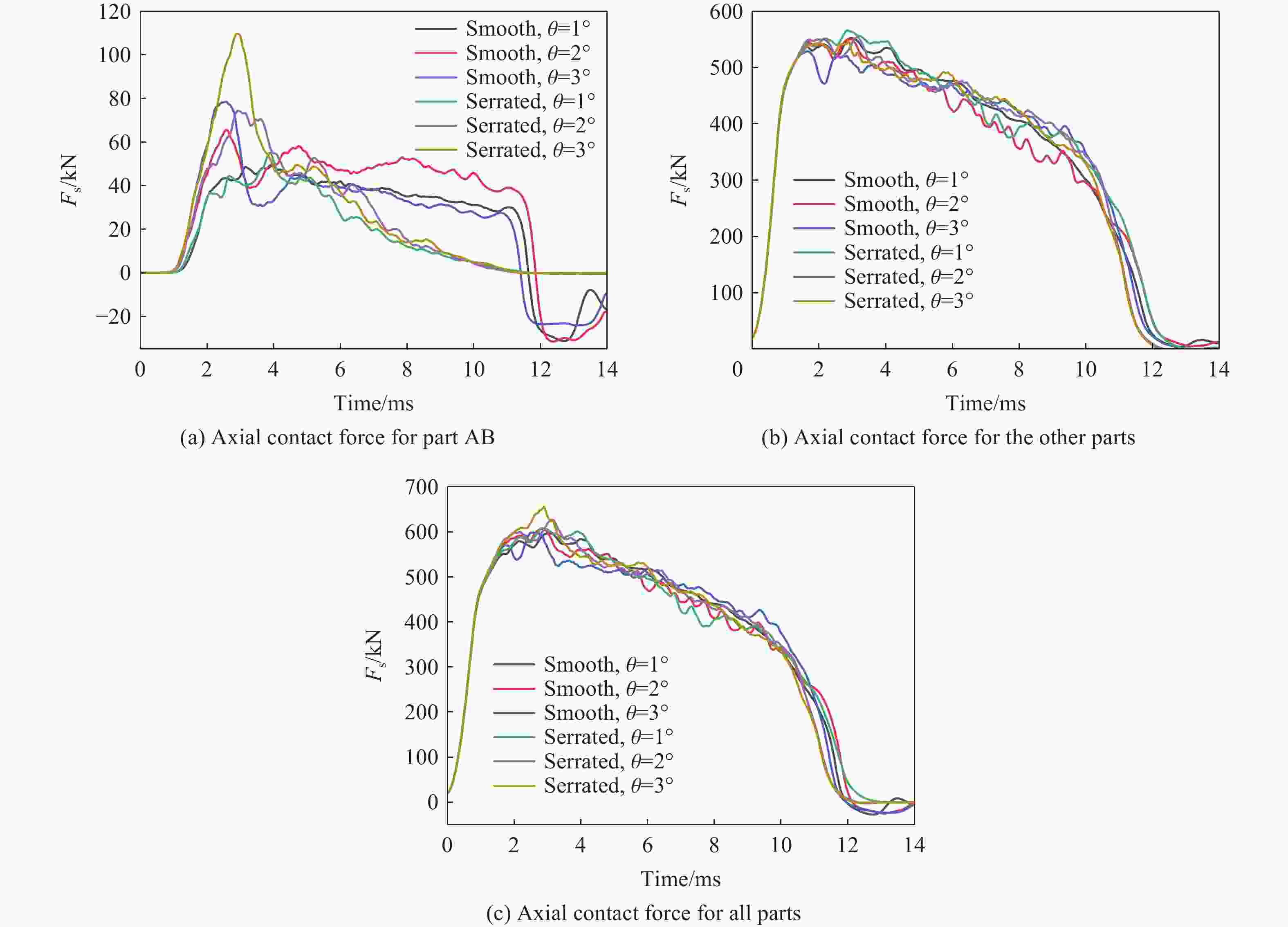
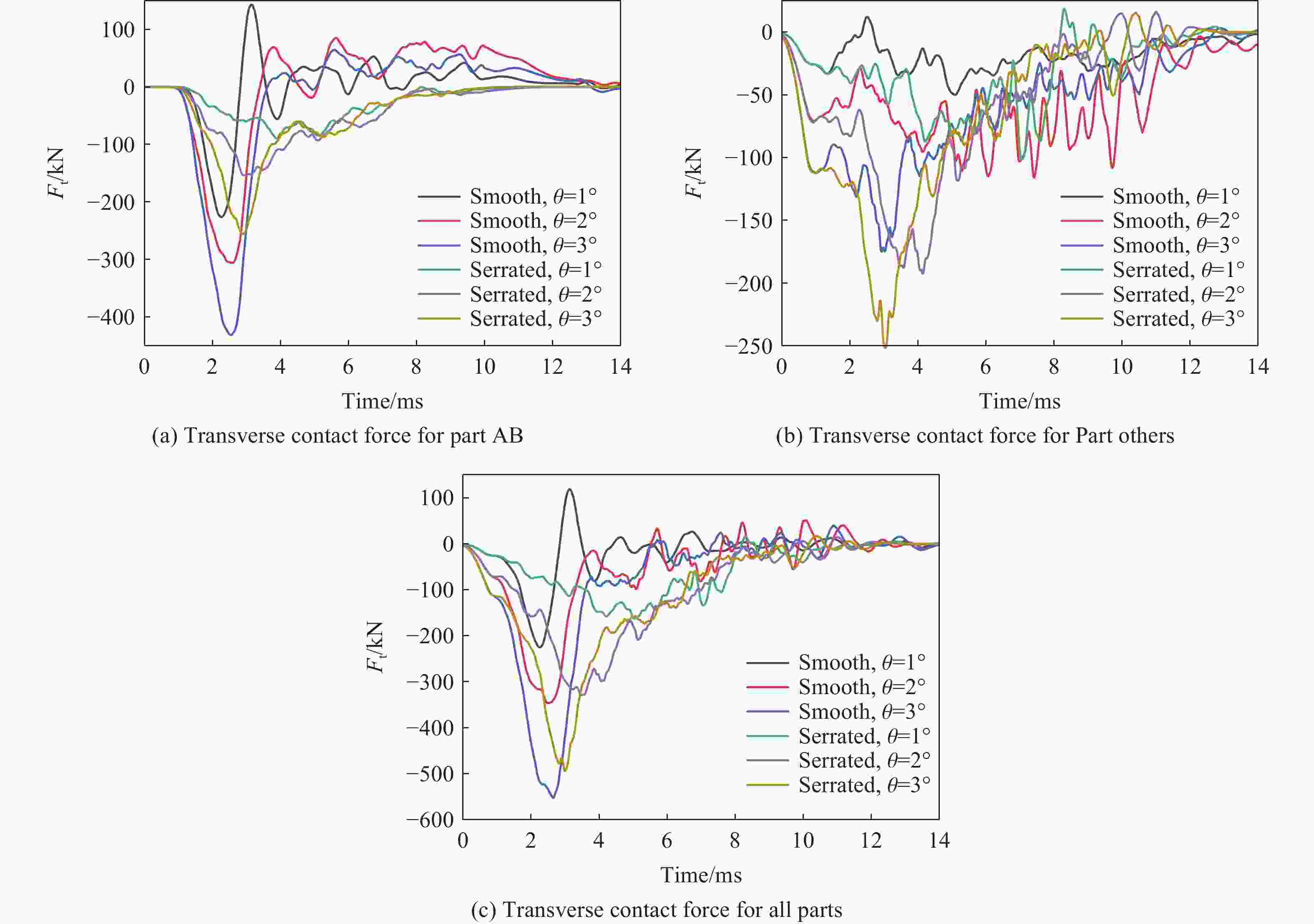
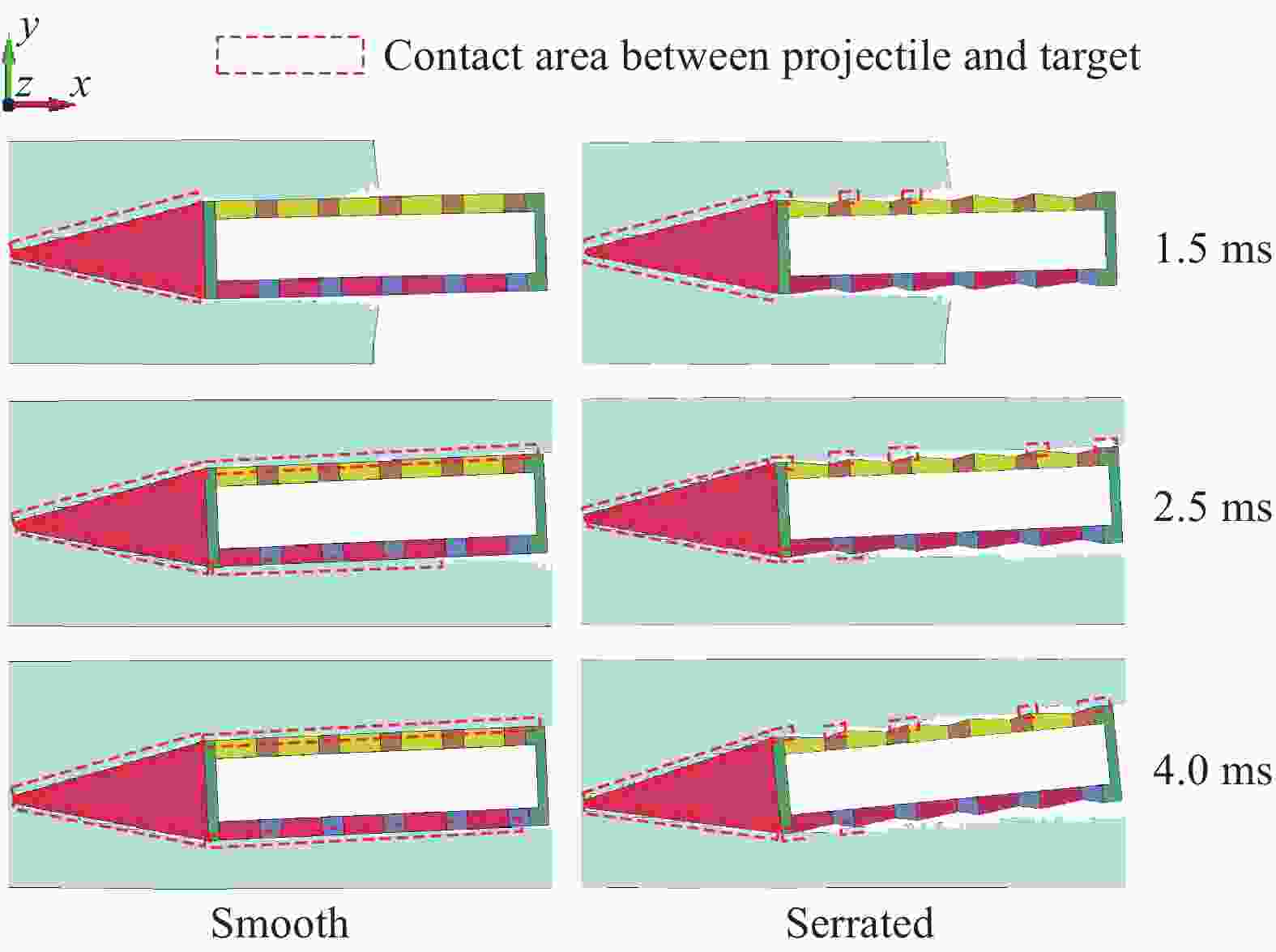
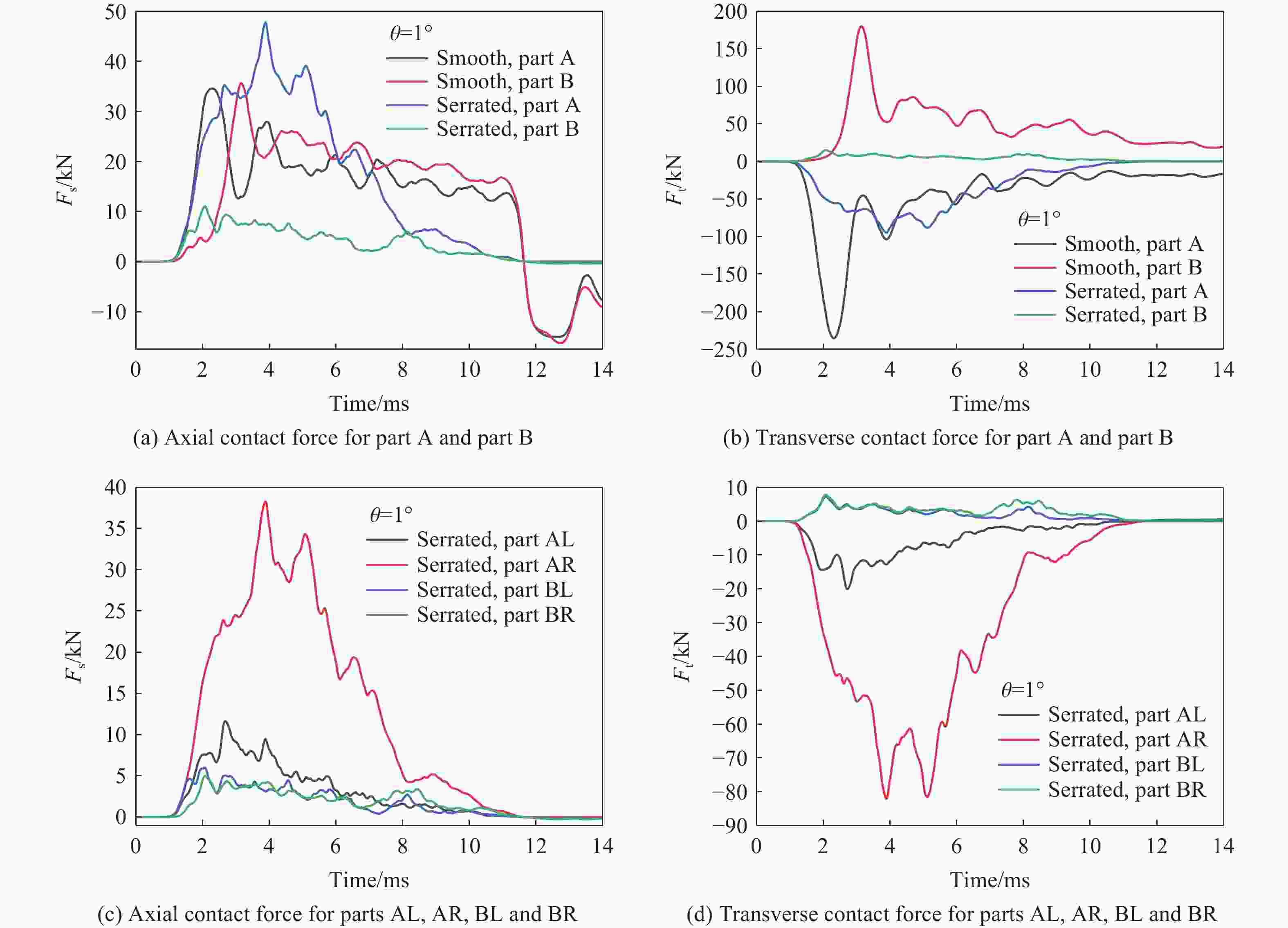
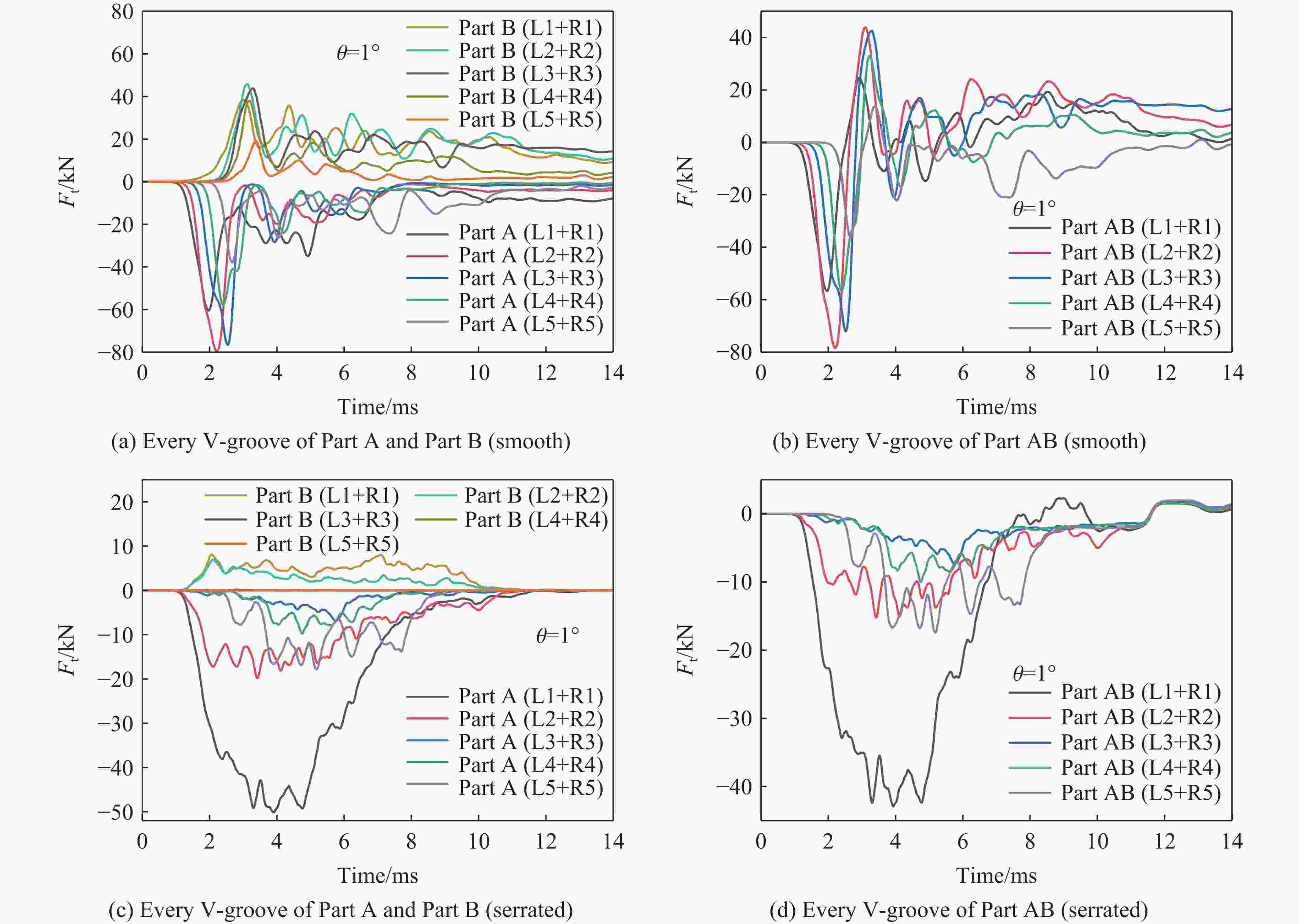
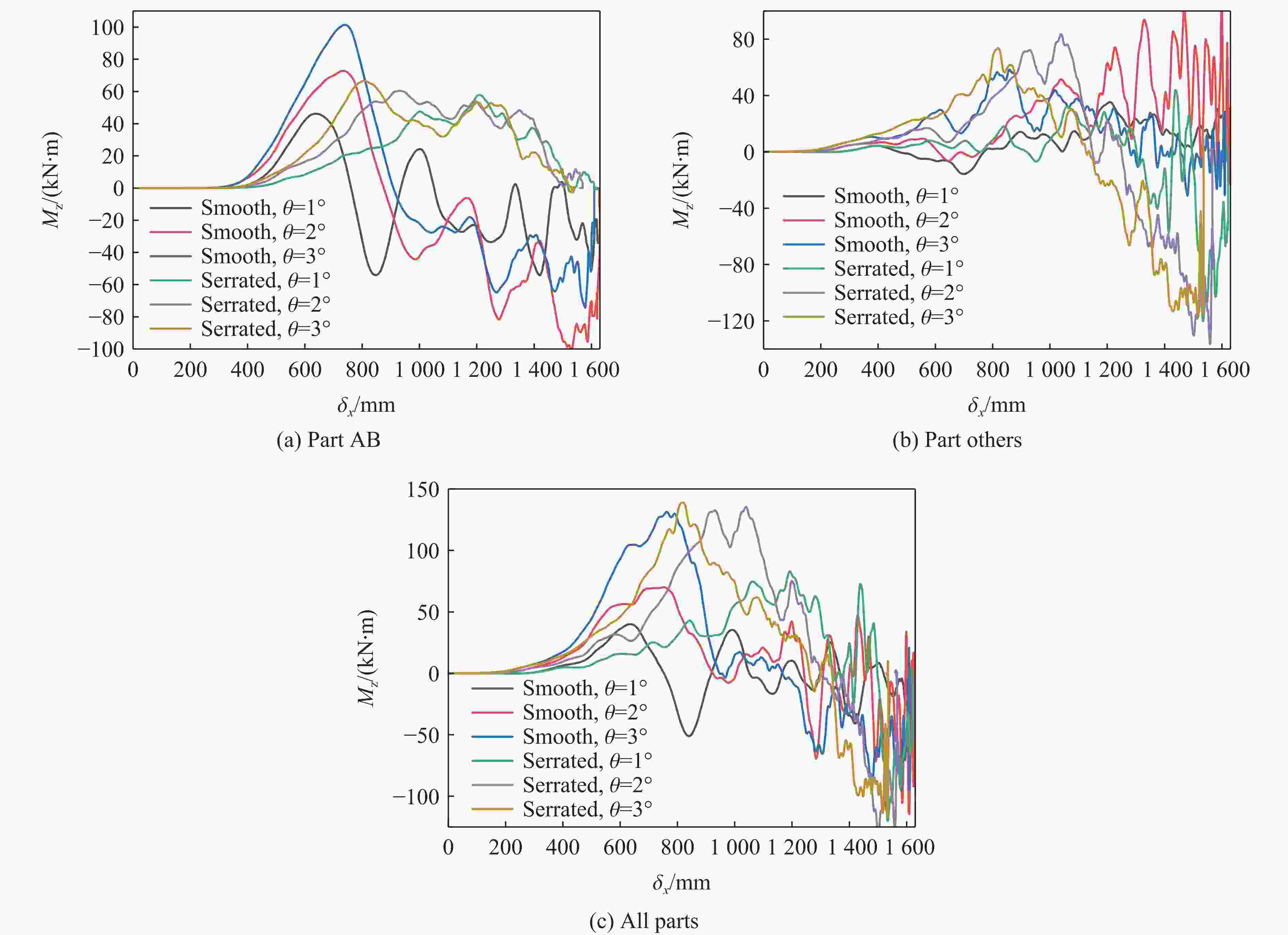
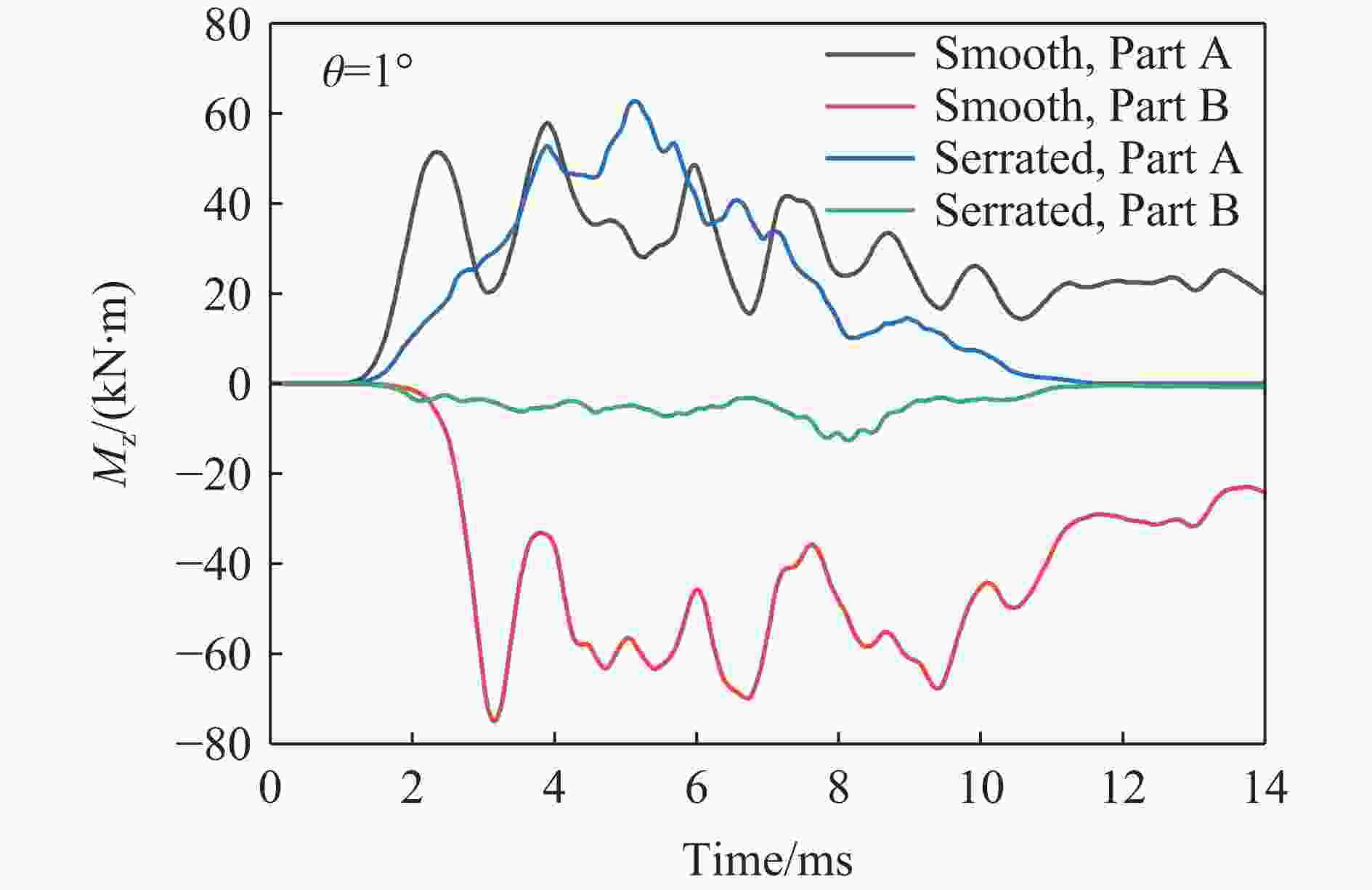
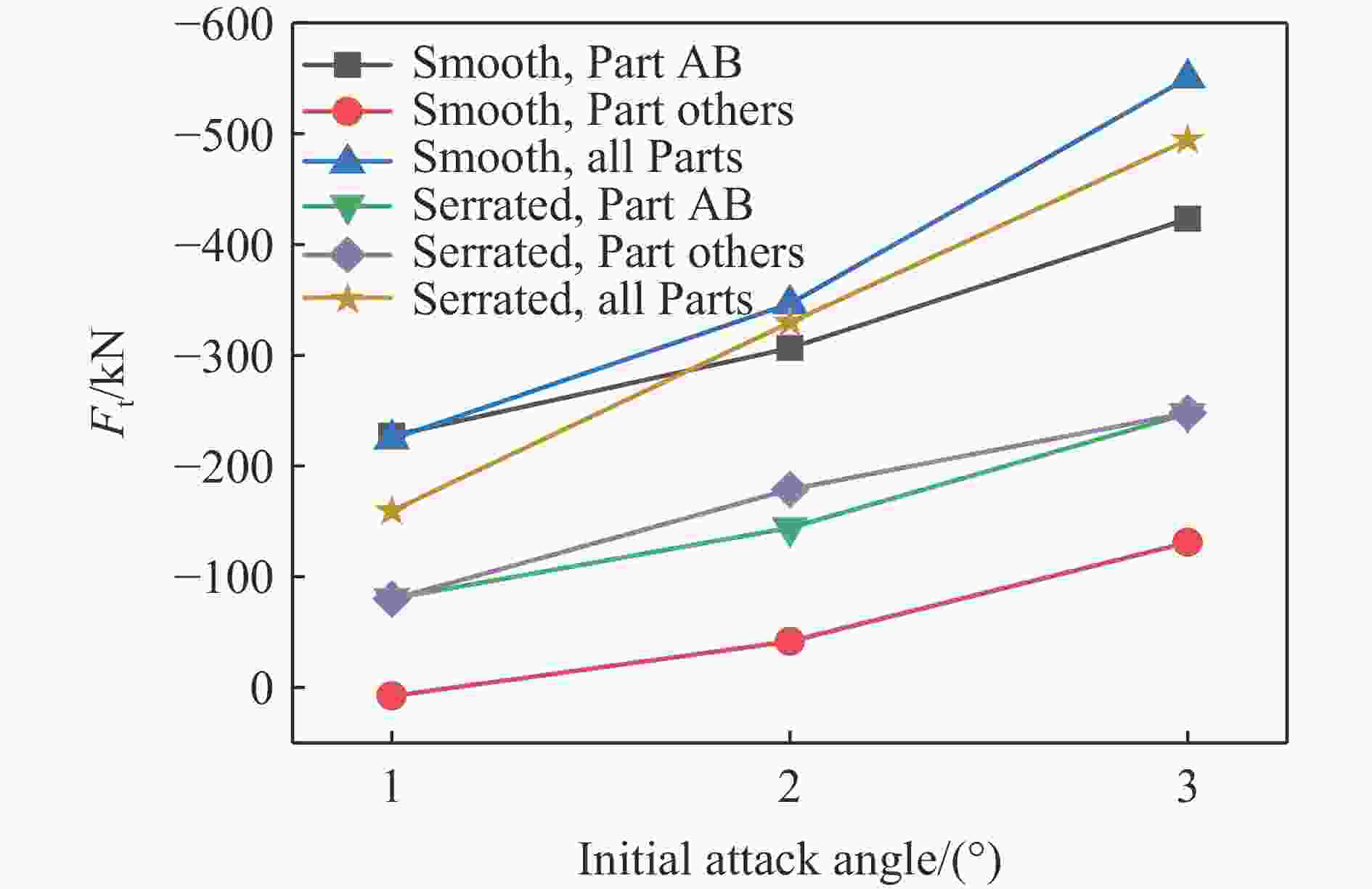
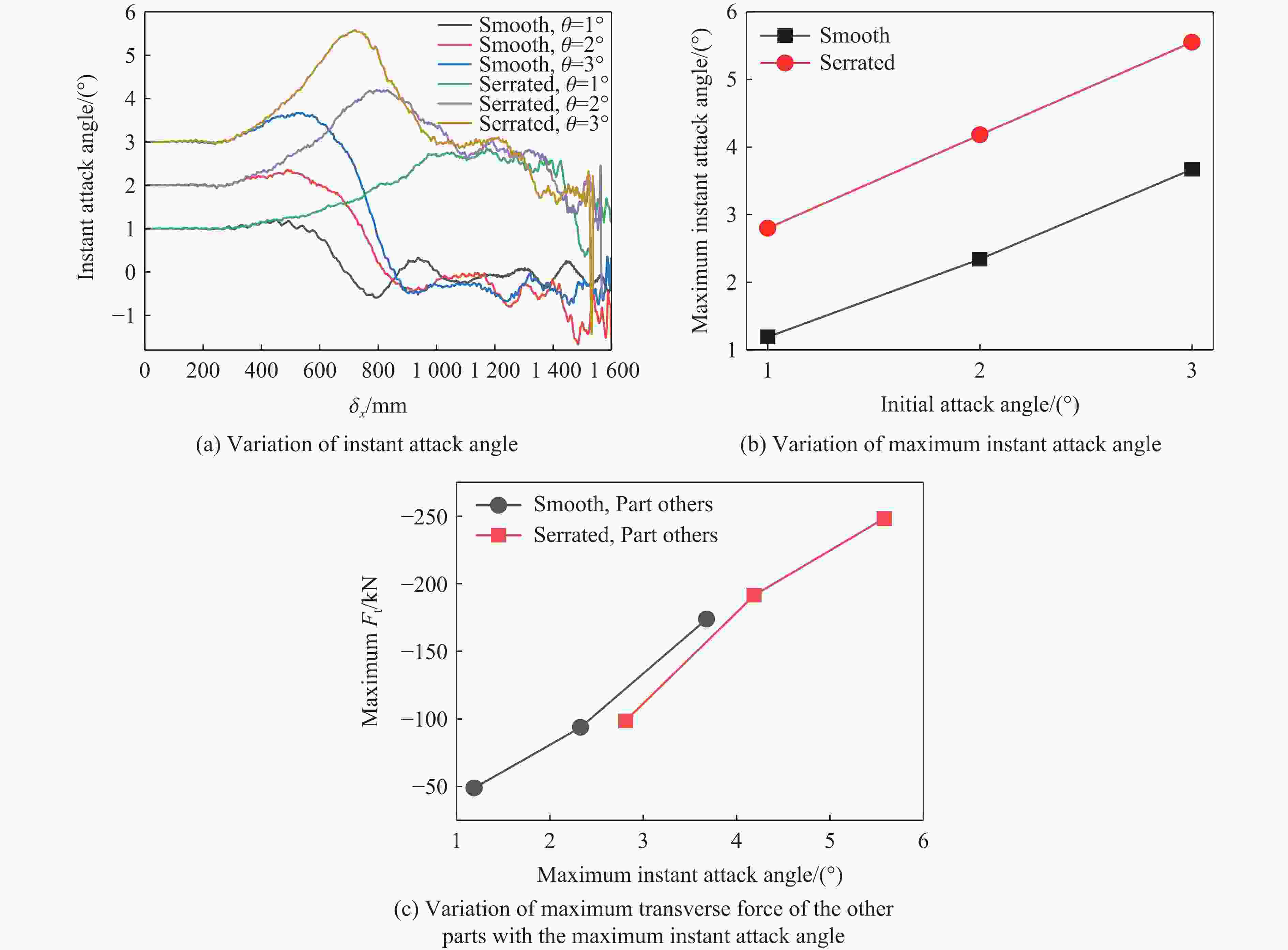
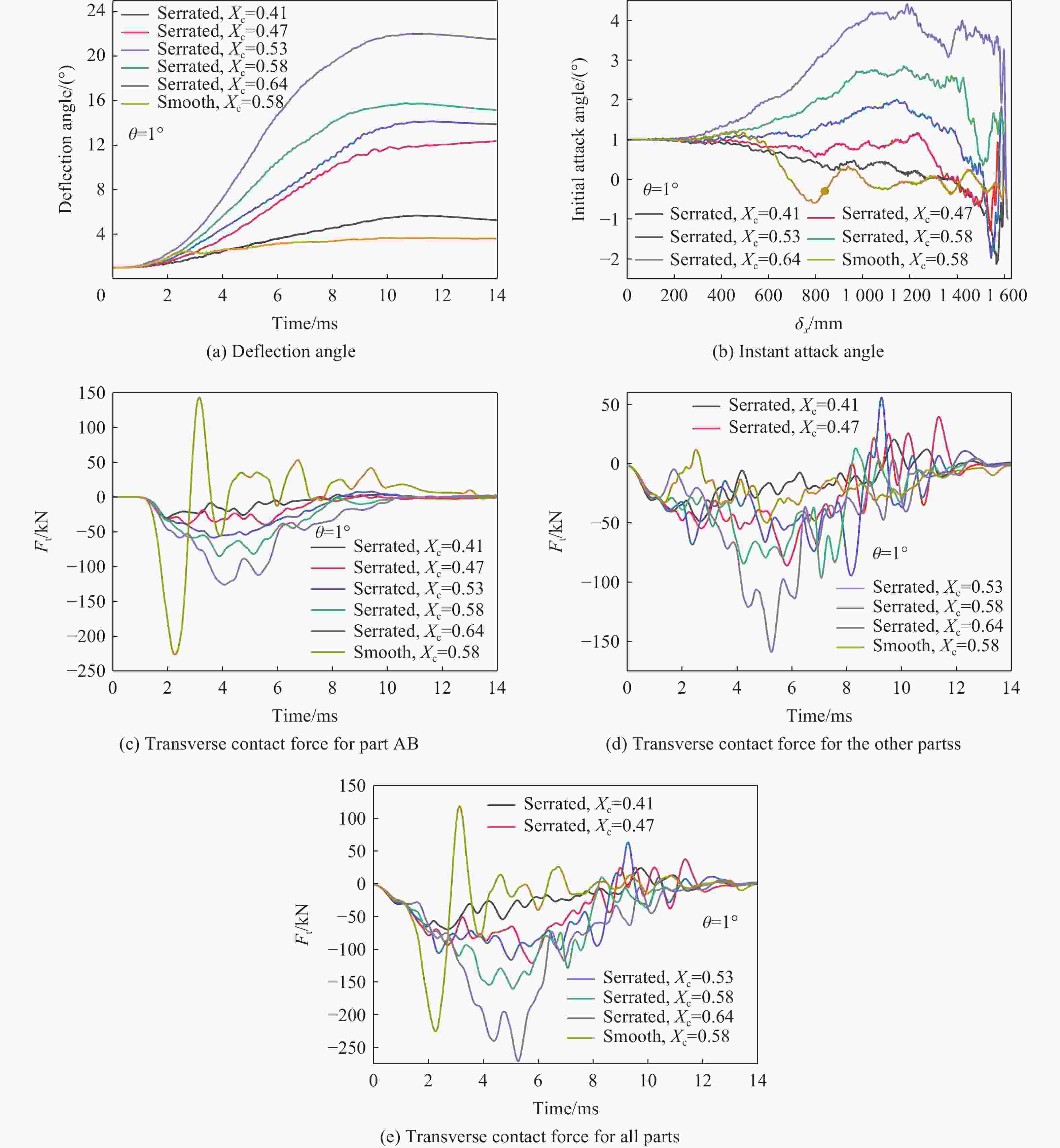
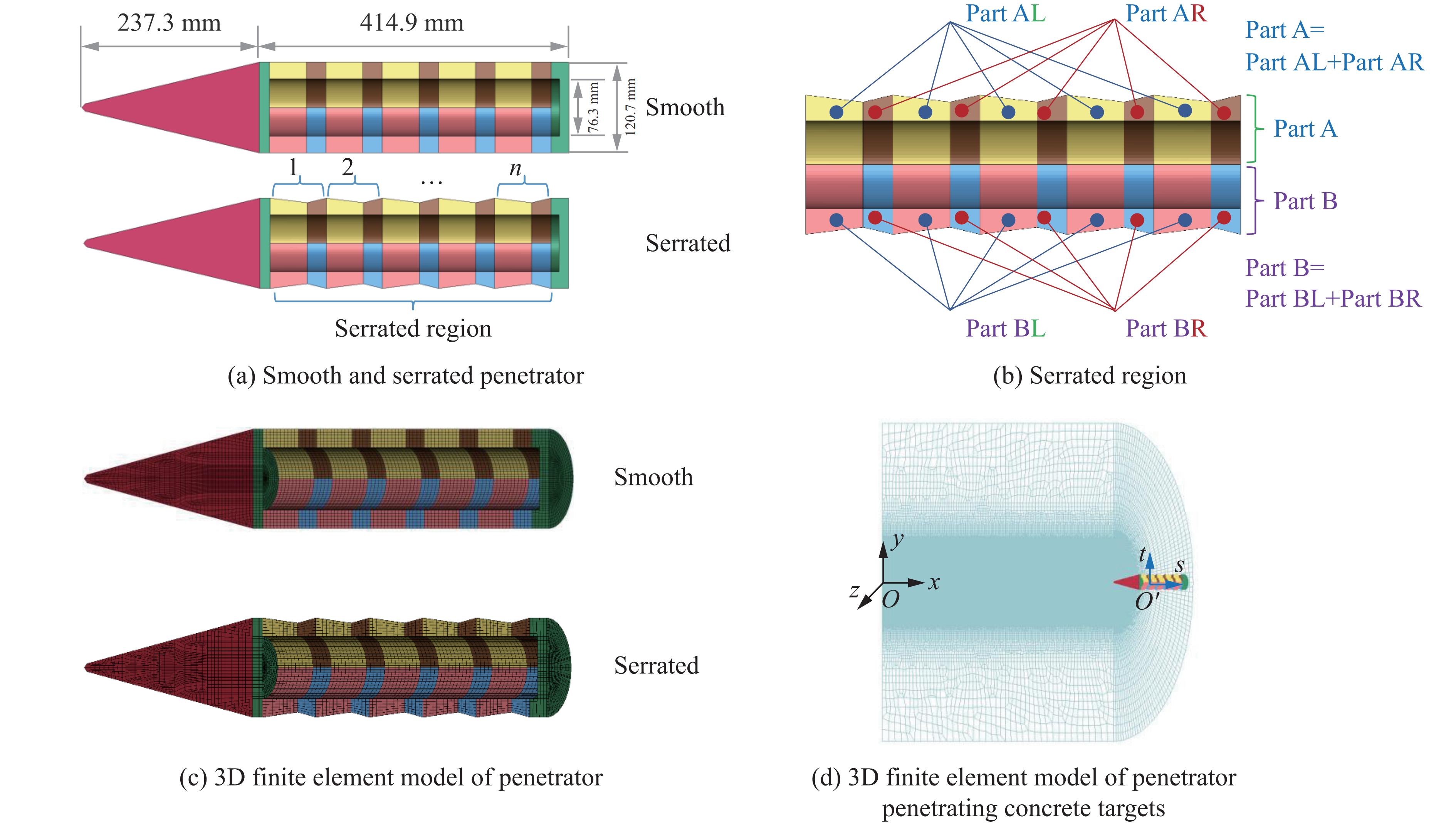
摘要: 为降低具有初始攻角的弹体在侵彻时产生的横向过载峰值，采用数值模拟方法，研究了一种带锯齿弹身的新型钻地弹以非零攻角姿态侵彻混凝土靶体时其特有的横向降载效应和机理。考虑初始攻角、质心系数等的影响，以常规光滑弹作为对比对象，分析了弹体运动规律、弹靶接触力、接触力矩、接触面积等。结果表明，在1°、2°和3°的小初始攻角范围内，锯齿弹较光滑弹分别降低横向过载峰值约30.6%、5.2%和11.3%，但相应的接触力矩的峰值和脉宽、偏转角度等均有所增大。研究结果揭示了锯齿弹的横向降载机理：锯齿弹身减小了弹靶的接触面积，横向接触力主要集中在弹身锯齿区靠近头部的前两个锯齿环槽的右锯齿上，使得锯齿弹身与靶的横向接触力减小，而非锯齿区（主要是弹体头部）与靶的横向接触力增大，二者的竞争可增强锯齿弹整体的横向降载效果。通过结构设计等手段抑制锯齿弹的弹道偏转后，可有效提升锯齿弹的横向降载效率。Abstract: In the process of deep penetration of the earth penetration weapon (EPW) attacking the underground target, the non-ideal penetration attitude with an initial attack angle is inevitable, which will introduce transverse overload with a large peak value for the earth penetrator. It could damage some important components of the earth-penetrating projectile and reduce the penetration efficiency of the projectile. Therefore, it is necessary to study the methodology of reducing the transverse overload peak value of the earth-penetrating projectile. However, the previous research on the earth-penetrating projectile seldom considered the influence of transverse overload, making it difficult to effectively reduce the transverse overload. In order to overcome this problem, a numerical simulation method was used to study the special transverse overload shedding effect and its mechanism of a new type of earth-penetrating projectile with a serrated configuration penetrating concrete targets at non-zero attack angles. The influences of the initial attack angle and the coefficient of the center of mass of the projectile were studied, and the motion, contact force, contact moment, and contact area of the projectile were analyzed using a conventional smooth projectile for comparison. The results show that for small initial attack angles of 1°, 2° and 3°, the peak value of transverse overload of the serrated projectile is reduced by about 30.6%, 5.2%, and 11.3%, respectively, compared to the smooth projectile but the peak value of contact moment, pulse width, and deflection angle are increased. The research reveals the mechanical mechanism to reduce transverse overload: the serrated body of the projectile reduces the contact area between the projectile and the target, and the transverse contact force is mainly concentrated on the upper surface of the right serrated parts of the first two serrated grooves near the head of the projectile; the transverse contact force between the serrated body and the target decreases, while the transverse contact force between the non-serrated parts (mainly the head of the projectile) and the target increases. Therefore, these two parts of the projectile compete and control the reduction effects of the transverse overload of the whole projectile in the process of deep penetration with an initial attack angle. When optimizations of structural design are used to suppress the ballistic deflection of the serrated projectile, the transverse overload shedding efficiency of serrated projectiles can be effectively improved.
-
为应对冲击动力学问题，人们发展了大量安全可靠的冲击防护结构[1-3]和高侵彻能力的武器装备[4-5]。现代化战争中，随着地面目标的加固防护及高价值目标等的深埋防护，使钻地武器成为有效打击和威慑此类目标的重要手段。为提高钻地弹的打击效率，在维持弹体结构完整性的前提下，需尽可能加大弹体的侵彻深度。通过优化弹头形状[6-10]、增大弹体长径比[11]、提高弹体初始撞击速度[12]、优化弹材和质量比[4]等，能够实现钻地弹最大侵彻深度的提升。然而，由于钻地过程中存在靶体不均匀及不对称性、弹体侵蚀和变形、弹体飞行时气动扰动等因素影响，实际弹体通常以非理想正侵彻姿态着靶，即弹体着靶的倾角和攻角非零，影响钻地弹的侵彻和打击能力[13]。
对非正侵彻过程中钻地弹的动力学问题已有很多研究[13-22]。非正侵彻姿态将引入垂直于弹轴的横向作用力。横向作用力一方面推动弹体沿垂直于弹体轴向的平动，另一方面促使弹体绕质心转动，从而减小弹体的有效侵彻深度。过大的横向作用力还可能导致弹体结构弯曲甚至被破坏，从而降低弹体的侵彻能力。与倾角相比，攻角对弹体偏转的影响更大。为此，学者们开展了抑制弹体偏转的研究，通过优化弹体质心系数[20]、弹身变径结构设计（尾裙等）[23-24]、弹体着靶姿态控制[13, 25]等提升弹体的弹道稳定性。若弹体在整个侵彻过程中均不发生明显的结构弯曲，常规设计的弹体在弹身全部埋入靶内后，弹道轨迹近似为直线[17, 26]。这说明在约一个弹长的侵深范围内，弹体的横向作用力及偏转力矩同时降至零。在如此短的侵深范围内将横向运动消除，说明弹体在此过程中承受了较大的横向加速度（过载），其峰值通常与轴向过载的峰值相当。较大的横向过载峰值可能损坏对过载方向敏感的弹载元器件。为此，本文中主要通过弹体外形设计降低弹体的横向过载峰值。
综上所述，学者们对维持深侵彻弹体的弹道稳定较为关注，希望在较短的侵深范围内消除弹体的横向运动，而对攻角引起的高横向过载峰值问题研究较少，甚少关注降低横向过载峰值的有效方法。2023年，Spawn[27]首次提出了一种锯齿弹身的钻地弹结构，并开展了数发素混凝土侵彻试验，研究结果表明，锯齿弹身外形具有横向降载作用，但该研究并未深入分析弹型结构侵彻的降载机理和影响因素。
本文中将采用数值模拟方法，进一步对比分析锯齿弹与常规光滑弹的侵彻动力学响应，研究弹体横向过载及弹道偏转规律，揭示锯齿弹的横向降载机理，以获得影响降载效果的关键因素及提高降载效率的方法。
1. 数值模拟模型
1.1 几何模型
为对比锯齿弹的侵彻效果，同时设计了一种等径圆柱弹身结构的光滑弹，如图1所示。两种弹体均主要由锥形弹头、弹身和尾盖组成，主要差异在于弹身结构，如图1（a）所示。光滑弹弹身为等径圆柱；锯齿弹的弹身表面均布数个V形环槽，环槽对称轴与弹体轴线重合，弹身剖面形状与锯齿相似。为突出两种弹型的弹身锯齿外形结构差异，忽略了文献[27]中两种弹体内部装填的硬回收装置，并将尾盖和弹身合并到一起。为研究锯齿弹弹身不同几何区域的受力特性，将锯齿区上下平分，上半区域和下半区域分别命名为Part A和Part B，进一步将Part A中所有锯齿的左锯齿和右锯齿分别命名为Part AL和Part AR，将Part B中所有锯齿的左锯齿和右锯齿分别命名为Part BL和Part BR，如图1（b）所示。此外，将锯齿区（即Part AB）以外的其他区域统称为Part others。为对比分析结果，将光滑弹采用相同的方式剖分。在构建数值仿真模型时，考虑弹体结构及侵彻条件的对称性，建立两种弹体三维结构的1/2有限元模型，如图1（c）所示。混凝土靶为圆柱体，直径为
2438.4 mm，高为2133.6 mm，建立的弹体侵彻混凝土靶体1/2有限元模型如图1（d）所示。
图 1 锯齿弹与光滑弹结构及有限元模型Figure 1. Configurations and numerical models of the smooth and serrated projectiles采用文献[27]中的光滑弹侵彻试验结果校核有限元模型。文献[27]中，该试验弹内部装填了硬回收装置，如图2（a）所示，相应的弹体1/2数值仿真模型如图2（b）所示。
将整体坐标系O-xyz固定在靶体上，局部坐标系O'-st固定在弹体上，如图1（d）所示。其中，坐标原点O固定在靶体底面圆心位置，局部坐标系原点O'固定在弹体质心上，x轴沿靶面法线方向并指向弹体，s轴沿弹体轴线方向，当正侵彻时x轴与s轴方向重合，当侵彻带攻角时，O-xy平面与O'-st平面重合。
在有限元模型中，利用八节点六面体单元对几何体进行离散，网格尺寸约5 mm，其中弹体模型共包含约3.7万个单元，靶体模型包含约321万个单元。两种弹型的弹体头部和尾盖的网格大小及数量完全相同，弹身沿轴向和环槽方向的网格数量也完全相同。弹头、弹身、尾盖之间的连接均简化为共节点约束。数值模拟采用拉格朗日显式有限元方法，并使用减缩积分单元，弹靶相互作用采用面面侵蚀接触表征，采用单元删除方法表征结构的破坏失效。对弹体施加沿x轴负方向的初始速度，其值为304 m/s（该速度属于亚声速范围），弹体和靶体在O-xy平面上施加对称边界条件，靶体底面固支。
1.2 材料模型
弹头、弹身及尾盖材料均为G50钢，试验弹内部硬回收部件材料为
7075 铝合金，采用弹塑性本构模型表征其材料力学性能，参数如表1所示。表 1 G50钢与7075铝合金弹塑性本构模型参数Table 1. Elastoplastic constitutive parameters of G50 steel and 7075 aluminum alloy材料 密度/
(g·cm−3)弹性模量/
GPa泊松比 屈服应力/
MPa切线模量/
MPaG50钢 7.8 200 0.3 1800 1000 7075 铝合金2.7 70 0.3 520 477 靶体为素混凝土，无约束抗压强度为12.3 MPa。采用HJC本构模型[28]表征其强度及损伤行为，材料参数引自文献[29]，如表2所示。其中，a为归一化内聚强度，b为归一化压力硬化参数，C为应变率系数，N为压力硬化指数，fc为无约束抗压强度，T为材料的最大拉伸应力，
˙ε0 为参考应变率，εe，min为使材料断裂的最小塑性应变，Fmax为归一化最大强度，pc为压溃压力，εc为压溃体积应变，pl为锁定压力，εl为锁定体积应变，D1、D2为模型的损伤常数，K1、K2、K3为压力常数。采用破坏应变作为混凝土材料的失效破坏准则，最大主应变和最大切应变参数均设置为0.2。密度/(g·cm−3) 剪切模量/GPa a b C N fc/MPa T/MPa ˙ε0/s−1 εe, min 1.604 1.15 0.28 1.85 0.006 0.84 12.3 1.8 1 0.01 Fmax pc/MPa εc pl/MPa εl D1 D2 K1/GPa K2/GPa K3/GPa 15.0 13.8 0.0075 1210 0.15 0.04 1.0 12 135 698 1.3 模型验证
基于文献[27]的试验测试，建立了图2中的光滑试验弹以1.7°的初始攻角侵彻混凝土靶的1/2对称有限元模型。数值仿真计算获得沿x轴方向的弹体侵彻深度为
1630 mm，相应试验测试结果为1616 mm[27]，两者偏差仅0.8%。弹体硬回收装置上轴向与横向加速度的仿真计算结果与试验测试结果对比如图3所示，其中，A表示加速度，下标s和t分别表示轴向和横向。二者轴向加速度的波形和幅值基本一致，加速度平台大约在3000 g（g表示重力加速度，g=9.8 m/s2）附近，试验弹加速度持续时间为11.1 ms，数值仿真所得加速度持续时间为11.8 ms，两者时间脉宽相对偏差仅6.3%；二者横向加速度的波形和幅值也基本一致，加速度峰值约3250 g，主波形的脉宽持续时间约为2.5 ms。总之，数值仿真获得的侵彻深度、加速度时间历程等与试验测试结果吻合良好，验证了数值模拟模型的有效性和合理性。
2. 侵彻动力学规律分析
2.1 弹体侵彻运动
为研究锯齿弹的运动学特性及动力学降载机理，对无初始攻角（即攻角为0°，理想正侵彻姿态）和初始攻角分别为1°、2°、3°时锯齿弹的运动学特性进行分析，并与光滑弹进行对比，弹体结构如图1所示。当弹体从右向左侵彻时，定义弹体绕逆时针方向偏转为正攻角。为消除两种构型弹体几何外形不同造成的质量差异，对左锯齿区、右锯齿区及其他区域的材料密度进行修正，使得两个弹体的总质量保持一致，均为33.5 kg（与文献[27]一致），且质心位置完全相同。这种修改密度的方法消除了两种弹型因质量与质心差异造成的侵彻响应差异，为进一步分析锯齿外形对弹体侵彻动力学影响的研究奠定了基础。两种弹型的计算工况如表3所示，其中Xc为质心系数，定义为弹体质心到弹尖的长度与整弹长度之比。
表 3 不同攻角时光滑弹与锯齿弹的侵彻工况设计Table 3. Penetration condition of smooth and serrated projectiles at different attack angles工况 弹体类型 初始攻角θ/（°） 质心系数Xc 左锯齿密度/(g·cm−3) 右锯齿密度/(g·cm−3) 其他区域密度/(g·cm−3) 1 光滑弹 0 0.58 8.525 8.525 8.525 2 锯齿弹 0 0.58 9.800 11.000 8.525 3 光滑弹 1 0.58 8.525 8.525 8.525 4 锯齿弹 1 0.58 9.800 11.000 8.525 5 光滑弹 2 0.58 8.525 8.525 8.525 6 锯齿弹 2 0.58 9.800 11.000 8.525 7 光滑弹 3 0.58 8.525 8.525 8.525 8 锯齿弹 3 0.58 9.800 11.000 8.525 理想正侵彻时，两种不同构型弹体的弹道轨迹对比如图4所示，整弹质心位置的位移和总体加速度对比如图5所示。其中，δ表示位移；采用傅里叶低通滤波的方法对加速度时间历程曲线进行滤波，滤波截止频率为1 kHz（后续接触力采用相同方法处理）。可见，光滑弹与锯齿弹弹道轨迹差异较小，在x轴方向的位移基本一致，如图4和图5（a）所示；在y轴方向两者位移均较小，其中光滑弹为4.4 mm、锯齿弹为6.3 mm，如图5（b）所示。光滑弹与锯齿弹的轴向加速度基本一致，如图5（c）所示，横向加速度均在0附近小幅震荡，如图5（d）所示。鉴于弹靶结构及着靶条件的对称性，理论上，0°攻角时弹体不应产生横向位移。然而，由于数值计算中存在沙漏，同时采用单元删除表征材料失效，因此，即使在理想正侵彻时，这些因素产生的数值扰动也将导致数值仿真中仍存在小幅横向力，从而产生小幅的弹体横向位移。基于相同的靶体网格及类似的弹体网格，数值分析对比显示，锯齿弹对数值扰动更敏感。
图 4 理想正侵彻时光滑弹与锯齿弹的弹道轨迹对比Figure 4. Comparison of ballistic trajectories between smooth and serrated projectiles during ideal normal penetration
图 5 理想正侵彻时光滑弹与锯齿弹的位移及加速度对比Figure 5. Comparison of displacements and accelerations between smooth and serrated projectiles during ideal normal penetration当初始攻角分别为1°、2°、3°时，光滑弹和锯齿弹的弹道轨迹均发生偏转，相同条件下，光滑弹的偏转小于锯齿弹，初始攻角越大，弹体偏转越明显，如图6所示。图7展示了不同初始攻角时光滑弹和锯齿弹的质心位置位移及弹体偏转角对比。分析三种不同的攻角情况，发现攻角对弹体沿x轴方向的位移影响较小，随着攻角的增大，两种弹型的最大侵深均略有减小；当初始攻角为1°和2°时，锯齿弹沿y轴的位移较光滑弹大，而当初始攻角为3°时，其沿y轴位移较光滑弹小，这说明攻角增大改变了锯齿弹对y轴位移的影响趋势；在不同初始攻角下，锯齿弹的最大偏转角明显大于光滑弹，且弹体偏转角保持增长的时间明显长于光滑弹。从数值上看，初始攻角分别为1°、2°、3°时，锯齿弹沿y轴位移分别比光滑弹增大91.1%、15.4%、−7.4%，最大偏转角分别增大318.9%、82.7%、49.2%，相对增大程度随初始攻角的增大而减小。
图 6 不同攻角时光滑弹及锯齿弹的弹道轨道对比Figure 6. Comparison of ballistic trajectories between smooth and serrated projectiles for different attack angles
图 7 不同攻角时光滑弹及锯齿弹位移及偏转角对比Figure 7. Comparison of displacements and deflection angles between smooth and serrated projectiles for different attack angles当初始攻角分别为1°、2°、3°时，光滑弹与锯齿弹的速度v及加速度曲线对比如图8所示。由图可知，对三种不同的攻角情况，初始攻角对两种弹型的轴向速度及加速度影响较小，二者基本一致，如图8（a）、（c）所示。不同初始攻角时，两种弹型的横向速度均出现了先明显增大、而后再减小并趋于零的变化趋势，相比而言，光滑弹的横向速度增加趋势不明显，如图8（b）所示。当初始攻角分别为1°、2°、3°时，锯齿弹的横向速度峰值分别比光滑弹增大60.5%、51.7%、34.0%。类似地，随着初始攻角的增大，两种弹型的横向加速度峰值增大，光滑弹的横向加速度峰值均大于同条件下的锯齿弹峰值，如图8（d）所示。当初始攻角分别为1°、2°、3°时，锯齿弹的横向加速度峰值分别比光滑弹降低30.6%、5.2%、11.3%。可见，锯齿弹具有较明显的降横向过载效果。
图 8 不同攻角时光滑弹及锯齿弹速度和加速度对比Figure 8. Comparison of velocities and accelerations between smooth and serrated projectiles for different attack angles综上所述，当以小的初始攻角侵彻混凝土靶体时，锯齿弹与光滑弹沿轴向（x轴）的运动几乎一致，体现在两种弹型沿x轴的位移、速度和加速度差异较小；然而，在横向（即y轴）上，相比于光滑弹，锯齿弹展现出了更大的偏转角和横向速度，但横向加速度峰值降低。
2.2 弹体与靶体的接触力
导致锯齿弹与光滑弹轴向及横向运动规律差异的本质原因是二者弹靶接触力的差异。鉴于两种弹体构型差异主要在弹身锯齿区域，以下将主要分析弹身锯齿区、非锯齿区（主要在弹体头部）及整个弹体与靶体的接触力的差异。
弹体锯齿区、非锯齿区及整个弹体与靶体的轴向接触力Fs变化曲线如图9所示。其中，F表示接触面上的合力。首先，针对轴向接触力，在锯齿区，光滑弹在侵彻初期形成一个明显的峰值，然后形成较稳定的平台及较宽的脉宽，而锯齿弹侵彻初期形成的峰值大于光滑弹，其后随时间逐渐降低，其变化规律显著区别于光滑弹，如图9（a）所示。在非锯齿区，两种弹型均形成脉宽较宽的平台，波形一致且相对差异很小，如图9（b）所示。此外，尽管锯齿区轴向接触力峰值相对差异显著，但将两者合成为总体的轴向接触力时，两种弹型相对差异几乎消失，且接触力波形及脉宽与图8（c）中的轴向加速度完全一致，如图9（c）所示。这是因为小攻角侵彻条件下，锯齿区的弹身提供的轴向接触力较非锯齿区的弹头部分接触力小约一个量级，两种构型的整个弹体的轴向接触力及轴向运动规律主要由弹头区域决定。
图 9 不同攻角时两种弹型的锯齿区与非锯齿区轴向接触力的对比Figure 9. Comparison of axial contact forces in serrated and non-serrated areas between smooth and serrated projectiles for different attack angles其次，针对横向接触力，弹体锯齿区、非锯齿区及整个弹体与靶体的横向接触力Ft变化曲线如图10所示。在锯齿区，两种弹型均在侵彻初期形成一个大的峰值，其后迅速降低，但锯齿弹峰值显著低于光滑弹、脉宽显著长于光滑弹，如图10（a）所示；在非锯齿区，锯齿弹峰值显著高于光滑弹，如图10（b）所示。尽管两种弹型在锯齿区与非锯齿区的横向接触力峰值大小相对关系相反，但将两个区域的横向接触力合成时，锯齿弹总横向接触力峰值仍然小于光滑弹，且两者接触力波形及脉宽与图8（d）中的横向加速度完全一致，如图10（c）所示。以上分析表明，锯齿弹锯齿区能够降低弹体与靶体的横向接触力的峰值，这是锯齿弹相比光滑弹具有横向降载能力的根本原因。
图 10 不同攻角时两种弹型锯齿区与非锯齿区横向接触力的对比Figure 10. Comparison of transverse contact forces in serrated and non-serrated areas between smooth and serrated projectiles for different attack angles2.3 不同锯齿区的受力规律
为进一步研究弹身锯齿区与靶体的相互作用机制，以1°初始攻角工况为例，从弹靶接触宏观形貌及弹身上下侧锯齿面、左右锯齿区及从弹头到弹尾的每个锯齿区三种不同视角进行深入分析。
首先，直观展示了在有限元模型1/2对称面上不同时刻光滑弹和锯齿弹的弹靶接触宏观形貌，如图11所示。由图可知，在弹体头部，无论是光滑弹还是锯齿弹，其上下表面均与靶体充分接触。对弹身区域，在侵彻初期（如图11中1.5 ms时），弹身尚未全部埋入靶体时，由于初始攻角的影响，两种弹型与靶接触面主要分布在弹身上表面；随着弹身全部埋入靶后（如图11中2.5、4.0 ms时），光滑弹上下两侧弹身均与靶体接触，但锯齿弹弹身与靶的接触面主要分布在弹身上表面及下表面最左端锯齿上，且主要集中在右锯齿。总体而言，锯齿区显著减小了锯齿弹与靶的接触面积，同时改变了弹身上下表面与靶的接触方式。
图 11 光滑弹与锯齿弹的弹靶接触形貌对比（1°攻角时）Figure 11. Comparison of contact morphologies of projectile and target between smooth and serrated projectiles when attack angle is 1°当初始攻角为1°时，两种弹型弹身上下两侧锯齿面（Part A、Part B）及其左右锯齿（Part AL、Part AR、Part BL、Part BR）的接触力随时间的变化历程，如图12所示。由图12（a）～（b）可知，对光滑弹，其上下锯齿面的轴向及横向接触力幅值及波形相似，轴向接触力方向相同，横向接触力方向相反，且下锯齿面接触力开始上升及到达峰值时间迟于上锯齿面约0.9 ms。然而，对锯齿弹，接触力主要分布在上锯齿面，其中轴向接触力的峰值高于光滑弹，但持续时间较短，而横向接触力峰值绝对值明显小于光滑弹，但持续时间相当。锯齿弹的下锯齿面横向接触力峰值小于上锯齿面，这意味着锯齿弹侵彻过程中弹身下表面几乎不能抑制整个弹体的横向运动，因而锯齿弹相比光滑弹具有更大的横向运动速度（如图8（b）所示）。进一步分析锯齿弹左、右锯齿的接触力，如图12（c）～（d）所示。可见，锯齿弹轴向接触力主要由上锯齿面的右锯齿承受，其最大接触力峰值为38.1 kN；而上锯齿面的左锯齿以及下锯齿面的左、右锯齿的相应最大接触力峰值仅分别为11.5、5.9、4.9 kN。类似地，横向接触力主要由上锯齿面的右锯齿承受，其最大接触力峰值为81.6 kN；上锯齿面的左锯齿以及下锯齿面的左、右锯齿的相应最大接触力峰值仅为20.2、7.0、7.5 kN。可见，锯齿弹仅上锯齿面右锯齿的轴向与横向接触力幅值最突出，其余锯齿接触力明显偏小。
图 12 锯齿区上下表面及左右锯齿接触力对比（1°攻角时）Figure 12. Comparison of contact forces between the upper and lower surfaces and the left and right parts in the serrated areas when attack angle is 1°两种构型弹体弹身的横向接触力沿弹尖至弹尾方向的变化趋势如图13所示。本文中分析的锯齿弹弹身共分布有5个V形环槽锯齿，光滑弹的区域划分参照锯齿弹。由图可知，针对光滑弹，无论是上锯齿面还是下锯齿面，或者是两个锯齿面之和，横向接触力沿弹尖至弹尾方向呈现峰值先增大再减小的变化趋势，最大值出现在弹身中部附近，如图13（a）～（b）所示。然而，针对锯齿弹，沿弹尖至弹尾方向，上锯齿面横向接触力先迅速减小再缓慢增大，最大值出现在最接近弹头的锯齿，其峰值为50.1 kN；下锯齿面的横向接触力持续减小，且由最接近弹头的2个锯齿承受，其峰值仅分别为7.8、6.7 kN，明显小于上锯齿面的峰值最大值，如图13（c）所示。由于不同V形环槽锯齿的接触力也主要由上锯齿面承受，因而从弹尖至弹尾，锯齿弹上下锯齿面横向力合力的分布也与上锯齿面分布相似，如图13（d）所示。
图 13 沿弹尖至弹尾方向两种构型弹体弹身横向接触力变化趋势对比（1°攻角时）Figure 13. Comparison of transverse contact forces of projectile bodies between smooth and serrated projectiles along the direction from head to tail when attack angle is 1°2.4 接触力矩及弹道偏转机制
锯齿弹相比于光滑弹的另一个显著运动特征在于锯齿弹具有更大的偏转角，为此，进一步分析两种弹体与靶体接触过程中所产生的接触力矩的差异，进而揭示锯齿弹的弹道偏转机制。
对比弹体锯齿区、非锯齿区及整个弹体与靶体的接触力矩（Mz）变化曲线，如图14所示。对锯齿区，光滑弹在侵彻初期形成正向的接触力矩，后期形成反向的接触力矩；而锯齿弹主要形成正向的接触力矩，如图14（a）所示。这说明锯齿弹与光滑弹在该区域与靶体的作用机理不同。对非锯齿区，在大约前
1200 mm侵彻深度内，锯齿弹接触力矩总体上稍大于光滑弹，且两者总体为正值；在剩余侵彻过程中，两者接触力矩的大小都有较大的波动，其中锯齿弹接触力矩总体为负值，如图14（b）所示。当将锯齿区与非锯齿区的接触力矩合成后，锯齿弹总体接触力矩峰值大于光滑弹，发生时间明显滞后于光滑弹，且接触力矩脉宽更宽，如图14（c）所示。这说明侵彻过程中锯齿弹将发生更大的偏转，这与图7（c）中偏转角的变化情况一致。此外，还可以发现，锯齿弹总体接触力矩峰值大于光滑弹，随着初始攻角的增大，两种弹型接触力矩峰值均增大。当初始攻击为3°时，锯齿弹总体接触力矩峰值仅为光滑弹的1.1倍，因而作用在锯齿弹上的最大力矩与光滑弹相当。这说明在限定小攻角范围内，若结构设计能够保证光滑弹不发生结构弯曲，则也可保证锯齿弹不发生结构弯曲。
图 14 不同攻角时两种弹型锯齿区与非锯齿区接触力矩的对比Figure 14. Comparison of contact moments between serrated and non-serrated areas for different attack angles当初始攻角为1°时，两种弹型弹身上下两侧锯齿面的接触力矩随时间的变化历程如图15所示。对光滑弹的上下锯齿面，接触力矩幅值及波形相似；但两个面的接触力矩方向相反，且下锯齿面力矩开始上升及达到峰值的时间迟于上锯齿面约0.9 ms。然而，对锯齿弹，接触力矩主要分布在上锯齿面，其中接触力矩的峰值稍高于光滑弹，但持续时间相对较短。此外，锯齿弹下锯齿面接触力矩峰值远小于上锯齿面，因而锯齿弹的弹身无反向的接触力矩（图14（a）），这意味着锯齿弹侵彻过程中弹身下表面几乎不能抑制弹体偏转，因而相比光滑弹具有更大的偏转角（图7（c））。
综上所述，光滑弹弹身在侵彻过程中上下两部分弹体均承受接触力及力矩的作用，接触力及接触力矩相似，但下锯齿面的最大值出现时间较上锯齿面滞后约0.9 ms；沿弹尖至弹尾方向，光滑弹弹身的中间部分横向接触力最大。锯齿弹的弹身接触力及接触力矩主要由上锯齿面承受，且主要集中在上锯齿面右锯齿上，主要由靠近头部的1～2个右锯齿承受，因而难以抑制弹体的横向运动及弹体偏转。这种接触力及接触力矩的变化趋势差异与图11中两种弹型与靶相互作用面积的直观差异表现完全一致。
3. 锯齿弹横向降载机理
3.1 锯齿弹身降载与非锯齿弹头增载的竞争机制
上述分析阐述了两种弹型弹身锯齿区（Part AB）及头部非锯齿区（Part others）与靶接触力及接触力矩的差异，研究发现，锯齿型弹身能够显著降低弹体与靶体的横向接触力峰值，进而降低弹体的横向过载。当初始攻角分别为1°、2°、3°时，锯齿弹弹身的横向接触力峰值较光滑弹分别降低60.5%、49.6%和41.2%（根据图10（a）），而总体横向过载仅分别降低30.6%、5.2%、11.3%（根据图8（d））。弹体总的横向降载能力明显弱于弹身的横向降载能力，且随攻角的增大，横向降载能力呈减小的趋势。由于弹体横向降载效果是弹身与弹头的综合体现，这说明锯齿弹弹身横向接触力降低的同时，非锯齿头部横向接触力升高，正如图10（b）中所示，锯齿弹弹头的横向接触力较光滑弹分别增加了96.4%、64.8%和43.1%。进一步对图8（d）中横向加速度最大时刻两种弹型锯齿区与非锯齿区的横向接触力进行对比，如图16所示。可见，当横向加速度最大时，两种弹型锯齿区和非锯齿区的横向接触力绝对值均随初始攻角增大而增大，且增长斜率基本一致。尽管锯齿弹锯齿区的横向接触力显著小于光滑弹对应区域，但非锯齿区横向接触力显著大于光滑弹对应区域，因而使得锯齿弹总体降载效果低于其弹身部分的降载效果。此外，尽管锯齿弹与光滑弹总的横向接触力差别不大，但是两者横向接触力均随攻角的增大而增大，因而使得降载百分比随攻角的增大而减小。以上分析表明，锯齿弹的锯齿弹身降低横向过载的同时，非锯齿头部的横向接触力增大，两者存在竞争效应。锯齿弹整体的横向降载效果随初始攻角的增大而减小。
图 16 横向加速度最大时锯齿弹与光滑弹弹身与头部横向接触力的对比Figure 16. Comparison of transverse contact forces between body and head of smooth and serrated projectiles when the transverse acceleration is maximum上述分析表明，初始攻角对弹体横向接触力及降载效果都有显著影响。一般情况下，横向接触力峰值随初始攻角的增大而增大（图10），横向降载效果随攻角的增大而减小。由于锯齿弹相比光滑弹更容易发生偏转，使得两种弹体在侵彻过程中的瞬时攻角变化规律产生差异，如图17（a）～（b）所示。无论是光滑弹还是锯齿弹，瞬时攻角在侵彻过程中均先增大后减小，锯齿弹的瞬时攻角显著大于光滑弹，如图17（a）所示。此外，锯齿弹非零瞬时攻角持续时间贯穿整个侵彻过程，远大于光滑弹，这说明在横向上锯齿弹与靶体作用时间更长，因而横向的速度、加速度、接触力以及接触力矩持续时间更长，如图8（b）和（d）、图10、图14所示。从图17（b）可见，瞬时攻角峰值与初始攻角近似呈线性关系，且锯齿弹大于光滑弹约2°左右。从图17（c）可知，弹体头部最大横向接触力峰值随最大瞬时攻角的增大而增大，并且两种弹型映射曲线几乎在一条直线上。以上分析进一步表明，导致锯齿弹横向降载效果降低的更深层次原因是锯齿弹在侵彻过程中产生的瞬时攻角显著大于光滑弹，使得相同初始攻角情况下锯齿弹的弹体头部产生更大的横向接触力，最终减弱了锯齿区弹身的降载效果。
图 17 不同攻角时两种弹型瞬时攻角及横向接触力的变化规律Figure 17. Variation of instant attack angles and transverse contact forces at different initial attack angles3.2 抑制弹道偏转后对降载效率的提升
对图14的分析表明，小攻角侵彻混凝土靶时，光滑弹受到逆时针方向的偏转力矩作用发生逆时针偏转；当弹体全部埋入靶内后，混凝土将作用于弹体一个反向的顺时针偏转力矩，抑制弹体进一步逆时针偏转。然而，由于锯齿弹与靶体的接触面积小于光滑弹，受到的抑制偏转力矩更小，最终弹体偏转角度更大。当偏转角增大时，侵彻过程中瞬时攻角也随之增大，进而导致锯齿弹横向降载效率降低。反之，通过抑制弹体弹道偏转则能提高弹体的横向降载能力。一般情况下，改变弹体结构、质心系数、增加尾裙等都可以抑制弹体的弹道偏转[15]。相比而言，改变质心系数的方法可以在有限元模型中通过修改弹体不同部件的密度方便实现。由于本文的主要研究目的是揭示锯齿弹的横向降载机理，因而本文将主要讨论质心位置改变抑制弹体偏转后对降载效果的影响，其他方法机理及效果是类似的。通过修改模型密度改变弹体质心位置，对1°初始攻角时5个不同质心系数的锯齿弹侵彻工况进行分析，并与工况3的光滑弹进行对比，如表4所示。
表 4 不同质心位置构型弹体侵彻工况Table 4. Penetration conditions of configurations of projectiles with different mass centers工况 弹体类型 初始攻角θ/（°） 质心系数Xc 左锯齿密度/(g·cm−3) 右锯齿密度/(g·cm−3) 其他区域密度/(g·cm−3) 9 锯齿弹 1 0.41 0.479 0.479 24.200 10 锯齿弹 1 0.47 3.721 3.721 18.985 11 锯齿弹 1 0.53 6.965 6.965 13.756 4 锯齿弹 1 0.58 11.000 11.000 9.800 12 锯齿弹 1 0.64 13.454 13.454 3.295 3 光滑弹 1 0.58 8.525 8.525 8.525 1°初始攻角时不同质心位置锯齿弹偏转角、瞬时攻角、弹身和头部接触力及接触力合力随时间的变化规律如图18所示。当弹体质心位置前移，即质心系数减小时，锯齿弹偏转角及瞬时攻角均显著减小，如图18（a）～（b）所示。相比而言，5个工况中，Xc=0.41时的锯齿弹偏转角和瞬时攻角与Xc=0.58时的光滑弹较为接近，可近似认为此时两者弹道偏转过程及程度相当，而其他4个工况的偏转角及瞬时攻角均显著大于光滑弹，弹道偏转程度明显更严重。而Xc=0.41时的锯齿弹非锯齿区的横向接触力也与Xc=0.58时的光滑弹较为接近，如图18（d）所示，因而此时光滑弹与锯齿弹的受力差异仅体现在弹身锯齿区。此外，在锯齿弹锯齿区及非锯齿区，横向接触力均随弹体质心位置的前移而显著减小。在质心前移前后，相比Xc=0.58时的光滑弹，锯齿弹锯齿区横向接触力峰值由光滑弹的56%减小到光滑弹的13%，而锯齿弹非锯齿区横向接触力的峰值由光滑弹的3.15倍减小到光滑弹的0.96倍。相比光滑弹，表4中5种工况锯齿弹的总横向接触力峰值分别降低−20.4%、29.2%、48.8%、45.9%、68.6%，如图18（c）～（e）所示。由于Xc=0.41时锯齿弹与光滑弹弹道的偏转程度相当，因而可近似认为，在相同的弹道偏转情况下，锯齿弹横向降载效率为光滑弹的68.6%，相比图8（d）中30.6%的降载效率，降载能力显著提升。
图 18 不同质心系数时锯齿弹偏转角、瞬时攻角、横向接触力变化趋势Figure 18. Variation of deflection angle, instant attack angle and transverse contact force for serrated projectiles with different mass centers4. 结 论
基于一种新型锯齿弹构型，通过对弹体小初始攻角侵彻混凝土靶体问题开展数值模拟分析，系统研究了锯齿弹不同于传统光滑弹的侵彻运动特征和弹靶间的受力作用规律，深入揭示了锯齿弹的横向降载机制，并提供了一种提升降载效率的方法。主要结论如下。
(1)当弹体以较小初始攻角侵彻时，与光滑弹相比，锯齿弹外形不损失弹体轴向侵彻能力，但可降低弹体横向过载峰值，同时伴随更大的弹体偏转角度。
(2)锯齿弹横向降载机理在于，弹身与靶体接触区域集中在弹体上部，且接触力主要由靠近头部的1～2个右锯齿承受，这使得锯齿弹弹身横向接触力降低，且难以抑制锯齿弹的弹道偏转。
(3)锯齿弹的易偏转特征将增大锯齿弹瞬时攻角，从而增加锯齿弹非锯齿区的横向接触力，锯齿弹身横向降载与非锯齿弹头横向增载相互竞争。随攻角增大，锯齿弹总的横向降载能力呈下降趋势。
(4)当弹体质量、质心位置、着靶速度及侵彻靶标相同，初始攻角分别为1°、2°和3°时，与光滑弹相比，锯齿弹横向过载峰值分别降低30.6%、5.2%和11.3%。若通过改变质心位置实现锯齿弹与光滑弹类似的弹道偏转，当初始攻角为1°时，与光滑弹相比，锯齿弹横向降载能力可提升至68.6%。
本文分析结果仅适用于亚声速小攻角侵彻工况，针对攻角倾角耦合、超声速侵彻、高强度靶标等更为复杂的侵彻条件，将在未来工作中进一步展开讨论与分析。对于锯齿可能引入的弹身抗弯极限强度降低问题，也将在未来工作中一并讨论。
-
图 1 锯齿弹与光滑弹结构及有限元模型
Figure 1. Configurations and numerical models of the smooth and serrated projectiles
图 4 理想正侵彻时光滑弹与锯齿弹的弹道轨迹对比
Figure 4. Comparison of ballistic trajectories between smooth and serrated projectiles during ideal normal penetration
图 5 理想正侵彻时光滑弹与锯齿弹的位移及加速度对比
Figure 5. Comparison of displacements and accelerations between smooth and serrated projectiles during ideal normal penetration
图 6 不同攻角时光滑弹及锯齿弹的弹道轨道对比
Figure 6. Comparison of ballistic trajectories between smooth and serrated projectiles for different attack angles
图 7 不同攻角时光滑弹及锯齿弹位移及偏转角对比
Figure 7. Comparison of displacements and deflection angles between smooth and serrated projectiles for different attack angles
图 8 不同攻角时光滑弹及锯齿弹速度和加速度对比
Figure 8. Comparison of velocities and accelerations between smooth and serrated projectiles for different attack angles
图 9 不同攻角时两种弹型的锯齿区与非锯齿区轴向接触力的对比
Figure 9. Comparison of axial contact forces in serrated and non-serrated areas between smooth and serrated projectiles for different attack angles
图 10 不同攻角时两种弹型锯齿区与非锯齿区横向接触力的对比
Figure 10. Comparison of transverse contact forces in serrated and non-serrated areas between smooth and serrated projectiles for different attack angles
图 11 光滑弹与锯齿弹的弹靶接触形貌对比（1°攻角时）
Figure 11. Comparison of contact morphologies of projectile and target between smooth and serrated projectiles when attack angle is 1°
图 12 锯齿区上下表面及左右锯齿接触力对比（1°攻角时）
Figure 12. Comparison of contact forces between the upper and lower surfaces and the left and right parts in the serrated areas when attack angle is 1°
图 13 沿弹尖至弹尾方向两种构型弹体弹身横向接触力变化趋势对比（1°攻角时）
Figure 13. Comparison of transverse contact forces of projectile bodies between smooth and serrated projectiles along the direction from head to tail when attack angle is 1°
图 14 不同攻角时两种弹型锯齿区与非锯齿区接触力矩的对比
Figure 14. Comparison of contact moments between serrated and non-serrated areas for different attack angles
图 16 横向加速度最大时锯齿弹与光滑弹弹身与头部横向接触力的对比
Figure 16. Comparison of transverse contact forces between body and head of smooth and serrated projectiles when the transverse acceleration is maximum
图 17 不同攻角时两种弹型瞬时攻角及横向接触力的变化规律
Figure 17. Variation of instant attack angles and transverse contact forces at different initial attack angles
图 18 不同质心系数时锯齿弹偏转角、瞬时攻角、横向接触力变化趋势
Figure 18. Variation of deflection angle, instant attack angle and transverse contact force for serrated projectiles with different mass centers
表 1 G50钢与7075铝合金弹塑性本构模型参数
Table 1. Elastoplastic constitutive parameters of G50 steel and 7075 aluminum alloy
材料 密度/
(g·cm−3)弹性模量/
GPa泊松比 屈服应力/
MPa切线模量/
MPaG50钢 7.8 200 0.3 1800 1000 7075 铝合金2.7 70 0.3 520 477 
下载: 导出CSV
密度/(g·cm−3) 剪切模量/GPa a b C N fc/MPa T/MPa ˙ε0/s−1 εe, min 1.604 1.15 0.28 1.85 0.006 0.84 12.3 1.8 1 0.01 Fmax pc/MPa εc pl/MPa εl D1 D2 K1/GPa K2/GPa K3/GPa 15.0 13.8 0.0075 1210 0.15 0.04 1.0 12 135 698
下载: 导出CSV
表 3 不同攻角时光滑弹与锯齿弹的侵彻工况设计
Table 3. Penetration condition of smooth and serrated projectiles at different attack angles
工况 弹体类型 初始攻角θ/（°） 质心系数Xc 左锯齿密度/(g·cm−3) 右锯齿密度/(g·cm−3) 其他区域密度/(g·cm−3) 1 光滑弹 0 0.58 8.525 8.525 8.525 2 锯齿弹 0 0.58 9.800 11.000 8.525 3 光滑弹 1 0.58 8.525 8.525 8.525 4 锯齿弹 1 0.58 9.800 11.000 8.525 5 光滑弹 2 0.58 8.525 8.525 8.525 6 锯齿弹 2 0.58 9.800 11.000 8.525 7 光滑弹 3 0.58 8.525 8.525 8.525 8 锯齿弹 3 0.58 9.800 11.000 8.525
下载: 导出CSV
表 4 不同质心位置构型弹体侵彻工况
Table 4. Penetration conditions of configurations of projectiles with different mass centers
工况 弹体类型 初始攻角θ/（°） 质心系数Xc 左锯齿密度/(g·cm−3) 右锯齿密度/(g·cm−3) 其他区域密度/(g·cm−3) 9 锯齿弹 1 0.41 0.479 0.479 24.200 10 锯齿弹 1 0.47 3.721 3.721 18.985 11 锯齿弹 1 0.53 6.965 6.965 13.756 4 锯齿弹 1 0.58 11.000 11.000 9.800 12 锯齿弹 1 0.64 13.454 13.454 3.295 3 光滑弹 1 0.58 8.525 8.525 8.525
下载: 导出CSV
-
[1] 余同希, 卢国兴, 张雄. 能量吸收: 结构与材料的力学行为和塑性分析 [M]. 北京: 科学出版社, 2019: 303–330. [2] 诺曼·琼斯. 结构冲击 [M]. 许骏, 蒋平, 译. 北京: 国防工业出版社, 2018: Ⅹ–Ⅺ.JONES N. Structural impact [M]. Translated by XU J, JIANG P. Beijing: National Defense Industry Press, 2018: Ⅹ–Ⅺ. [3] WANG S, XU F, ZHANG X Y, et al. A directional framework of similarity laws for geometrically distorted structures subjected to impact loads [J]. International Journal of Impact Engineering, 2022, 161: 104092. DOI: 10.1016/j.ijimpeng.2021.104092. [4] 陈小伟. 穿甲/侵彻力学的理论建模与分析 [M]. 北京: 科学出版社, 2019: 281–470.CHEN X W. Modelling on the perforation and penetration [M]. Beijing: Science Press, 2019: 281–470. [5] BEN-DOR G, DUBINSKY A, ELPERIN T. 高速侵彻动力学: 工程模型和方法 [M]. 武海军, 黄风雷, 皮爱国, 译. 北京: 科学出版社, 2020: 241–298.BEN-DOR G, DUBINSKY A, ELPERIN T. High-speed penetration dynamics: engineering models and methods [M]. Translated by WU H J, HUANG F L, PI A G. Beijing: Science Press, 2020: 241–298. [6] JONES S E, RULE W K, JEROME D M, et al. On the optimal nose geometry for a rigid penetrator [J]. Computational Mechanics, 1998, 22(5): 413–417. DOI: 10.1007/s004660050373. [7] BEN-DOR G, DUBINSKY A, ELPERIN T. Shape optimization of impactor penetrating into concrete or limestone targets [J]. International Journal of Solids and Structures, 2003, 40(17): 4487–4500. DOI: 10.1016/S0020-7683(03)00212-9. [8] 刘坚成, 黄风雷, 皮爱国, 等. 异型头部弹体增强侵彻性能机理研究 [J]. 爆炸与冲击, 2014, 34(4): 409–414. DOI: 10.11883/1001-1455(2014)04-0409-06.LIU J C, HUANG F L, PI A G, et al. On enhanced penetration performance of modified nose projectiles [J]. Explosion and Shock Waves, 2014, 34(4): 409–414. DOI: 10.11883/1001-1455(2014)04-0409-06. [9] 柴传国, 武海军, 皮爱国, 等. 异形头部弹体中低速侵彻混凝土的实验研究 [J]. 北京理工大学学报, 2015, 35(8): 787–791. DOI: 10.15918/j.tbit1001-0645.2015.08.004.CHAI C G, WU H J, PI A G, et al. Experimental study on nose headed penetrator penetrating to concrete target with middle and low speed [J]. Transactions of Beijing Institute of Technology, 2015, 35(8): 787–791. DOI: 10.15918/j.tbit1001-0645.2015.08.004. [10] 张欣欣, 武海军, 黄风雷, 等. 刻槽弹侵彻混凝土受力模型研究 [J]. 爆炸与冲击, 2016, 36(1): 75–80. DOI: 10.11883/1001-1455(2016)01-0075-06.ZHANG X X, WU H J, HUANG F L, et al. Mechanical model of the grooved-tapered projectile penetrating concrete targets [J]. Explosion and Shock Waves, 2016, 36(1): 75–80. DOI: 10.11883/1001-1455(2016)01-0075-06. [11] 皮爱国, 黄风雷. 大长细比动能弹体弹塑性动力响应数值模拟 [J]. 北京理工大学学报, 2007, 27(8): 666–670. DOI: 10.3969/j.issn.1001-0645.2007.08.003.PI A G, HUANG F L. Numerical simulation of the elastic-plastic dynamic response of a slender kinetic energy penetrator [J]. Transactions of Beijing Institute of Technology, 2007, 27(8): 666–670. DOI: 10.3969/j.issn.1001-0645.2007.08.003. [12] CHEN X W, LI Q M. Deep penetration of a non-deformable projectile with different geometrical characteristics [J]. International Journal of Impact Engineering, 2002, 27(6): 619–637. DOI: 10.1016/S0734-743X(02)00005-2. [13] 高旭东, 李庆明. 带攻角斜侵彻混凝土的弹道偏转分析 [J]. 兵工学报, 2014, 35(S2): 33–39.GAO X D, LI Q M. Trajectory analysis of projectile obliquely penetrating into concrete target at attack angle [J]. Acta Armamentarii, 2014, 35(S2): 33–39. [14] 尹放林, 王明洋, 钱七虎, 等. 弹丸斜入射对侵彻深度的影响 [J]. 爆炸与冲击, 1998, 18(1): 69–76. DOI: 10.11883/1001-1455(1998)01-0069-8.YIN F L, WANG M Y, QIAN Q H, et al. Penetration depth of projectile oblique into target [J]. Explosion and Shock Waves, 1998, 18(1): 69–76. DOI: 10.11883/1001-1455(1998)01-0069-8. [15] 闪雨, 黄风雷, 武海军, 等. 动能弹非正侵彻弹道稳定性研究 [C]//第六届全国强动载效应及防护学术会议暨2014年复杂介质/结构的动态力学行为创新研究群体学术研讨会论文集. 北京: 中国力学学会爆炸力学专业委员会, 2014: 450–459. [16] 段卓平, 李淑睿, 马兆芳, 等. 刚性弹体斜侵彻贯穿混凝土靶的姿态偏转理论模型 [J]. 爆炸与冲击, 2019, 39(6): 063302. DOI: 10.11883/bzycj-2018-0411.DUAN Z P, LI S R, MA Z F, et al. Analytical model for attitude deflection of rigid projectile during oblique perforation of concrete targets [J]. Explosion and Shock Waves, 2019, 39(6): 063302. DOI: 10.11883/bzycj-2018-0411. [17] 何丽灵, 郭虎, 陈小伟, 等. 结构变形对深侵彻弹体偏转的影响 [J]. 爆炸与冲击, 2023, 43(9): 091404. DOI: 10.11883/bzycj-2023-0068.HE L L, GUO H, CHEN X W, et al. Influence of structural deformation on the deflection of penetrator into concrete target with deep penetration [J]. Explosion and Shock Waves, 2023, 43(9): 091404. DOI: 10.11883/bzycj-2023-0068. [18] WARREN T L, HANCHAK S J, POORMON K L. Penetration of limestone targets by ogive-nosed VAR 4340 steel projectiles at oblique angles: experiments and simulations [J]. International Journal of Impact Engineering, 2004, 30(10): 1307–1331. DOI: 10.1016/j.ijimpeng.2003.09.047. [19] 马爱娥, 黄风雷, 初哲, 等. 弹体攻角侵彻混凝土数值模拟 [J]. 爆炸与冲击, 2008, 28(1): 33–37. DOI: 10.11883/1001-1455(2008)01-0033-05.MA A E, HUANG F L, CHU Z, et al. Numerical simulation on yawed penetration into concrete [J]. Explosion and Shock Waves, 2008, 28(1): 33–37. DOI: 10.11883/1001-1455(2008)01-0033-05. [20] BERNARD R S, CREIGHTON D C. Projectile penetration in soil and rock: analysis for non-normal impact: SL-79-15 [R]. USA: Vicksbury: Army Engineer Waterways Experiment Station Strutures Laboratory, 1979. [21] 吕中杰, 徐钰巍, 黄风雷. 弹体斜侵彻混凝土过程中的方向偏转 [J]. 兵工学报, 2009, 30(S2): 301–304.LYU Z J, XU Y W, HUANG F L. Transverse deflection of projectile obliquely penetrating into concrete [J]. Acta Armamentarii, 2009, 30(S2): 301–304. [22] 王可慧, 宁建国, 李志康, 等. 高速弹体非正侵彻混凝土靶的弹道偏转实验研究 [J]. 高压物理学报, 2013, 27(4): 561–566. DOI: 10.11858/gywlxb.2013.04.015.WANG K H, NING J G, LI Z K, et al. Ballistic trajectory of high-velocity projectile obliquely penetrating concrete target [J]. Chinese Journal of High Pressure Physics, 2013, 27(4): 561–566. DOI: 10.11858/gywlxb.2013.04.015. [23] 武海军, 黄风雷, 王一楠. 高速弹体非正侵彻混凝土试验研究 [C]//第八届全国爆炸力学学术会议论文集. 吉安: 中国力学学会爆炸力学专业委员会, 2007: 488–494. [24] 康海峰, 代廷静, 沈培辉, 等. 弹体形状对侵彻弹道的影响分析 [J]. 弹箭与制导学报, 2012, 32(2): 73–76. DOI: 10.3969/j.issn.1673-9728.2012.02.020.KANG H F, DAI T J, SHEN P H, et al. The analysis of the influence of projectile’s shape on penetration trajectory [J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2012, 32(2): 73–76. DOI: 10.3969/j.issn.1673-9728.2012.02.020. [25] 郭松林, 高世桥, 李泽章, 等. 弹引系统攻角侵彻混凝土仿真与试验研究 [J]. 兵器装备工程学报, 2022, 43(1): 135–139, 205. DOI: 10.11809/bqzbgcxb2022.01.021.GUO S L, GAO S Q, LI Z Z, et al. Experiment and simulation of projectile obliquely penetrating into concrete target at attack angle [J]. Journal of Ordnance Equipment Engineering, 2022, 43(1): 135–139, 205. DOI: 10.11809/bqzbgcxb2022.01.021. [26] 郭虎, 何丽灵, 陈小伟, 等. 球形颗粒遮弹层对高速侵彻弹体的作用机理 [J]. 爆炸与冲击, 2020, 40(10): 103301. DOI: 10.11883/bzycj-2019-0428.GUO H, HE L L, CHEN X W, et al. Penetration mechanism of a high-speed projectile into a shelter made of spherical aggregates [J]. Explosion and Shock Waves, 2020, 40(10): 103301. DOI: 10.11883/bzycj-2019-0428. [27] SPAWN C M. Field testing of earth penetrators: LA-UR-23-21935 [R]. Los Alamos: Los Alamos National Laboratory, 2023. DOI: 10.2172/1958976. [28] HOLMQUIST T J, JOHNSON G R, COOK W H. A computational constitutive model for concrete subjected to large strains, high strain rates and high pressures [C]//The 14th International Symposium on Ballistic. Quebec, 1993: 591–600. [29] 任根茂, 吴昊, 方秦, 等. 普通混凝土HJC本构模型参数确定 [J]. 振动与冲击, 2016, 35(18): 9–16. DOI: 10.13465/j.cnki.jvs.2016.18.002.REN G M, WU H, FANG Q, et al. Determinations of HJC constitutive model parameters for normal strength concrete [J]. Journal of Vibration and Shock, 2016, 35(18): 9–16. DOI: 10.13465/j.cnki.jvs.2016.18.002. -
下载:
计量
- 文章访问数: 186
- HTML全文浏览量: 72
- PDF下载量: 72
- 被引次数: 0