不同长径比下圆柱套筒的破片初速轴向分布

毕伟新; 李伟兵; 李军宝; 朱炜; 李文彬

doi:10.11883/bzycj-2024-0294

不同长径比下圆柱套筒的破片初速轴向分布

doi: 10.11883/bzycj-2024-0294

南京理工大学智能弹药技术国防重点学科实验室，江苏南京 210094

基金项目: 国家自然科学基金（12302437）；

详细信息

作者简介:
毕伟新（1993－　），男，博士研究生，1400219206@qq.com

通讯作者:
李伟兵（1982－　），男，博士，教授，njustlwb@163.com

中图分类号: O381; TJ410
计量
- 文章访问数: 162
- HTML全文浏览量: 35
- PDF下载量: 73
- 被引次数: 0
出版历程
- 收稿日期: 2024-08-19
- 修回日期: 2024-11-06
- 网络出版日期: 2024-11-11
- 刊出日期: 2025-08-01

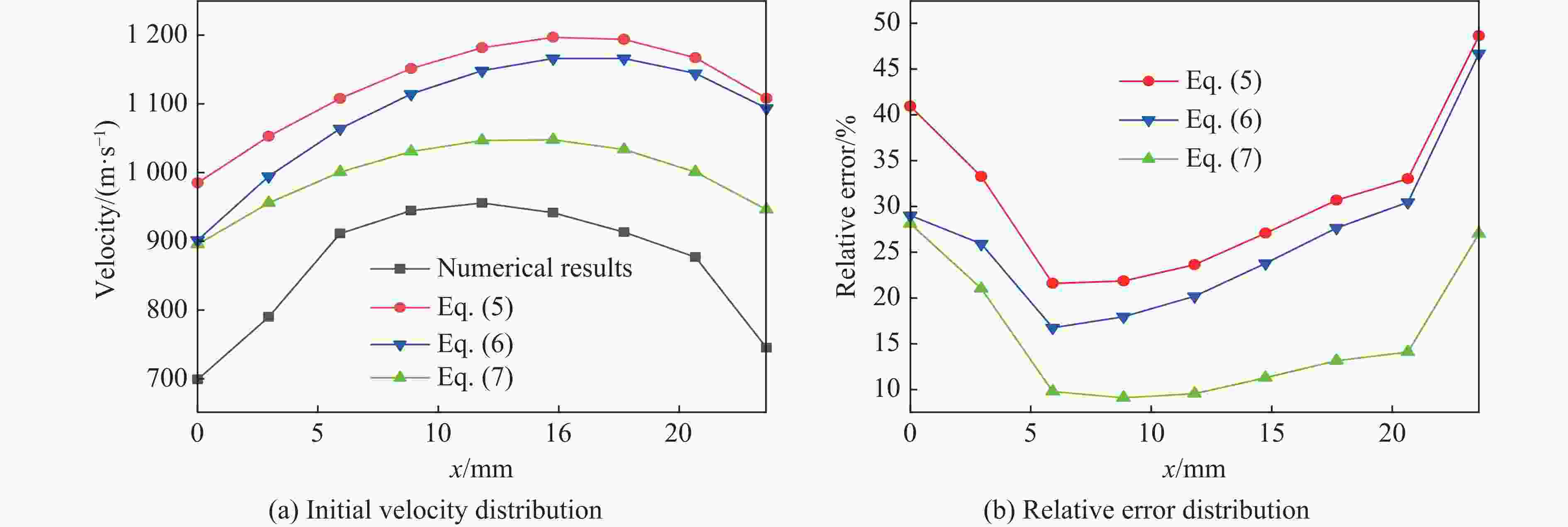
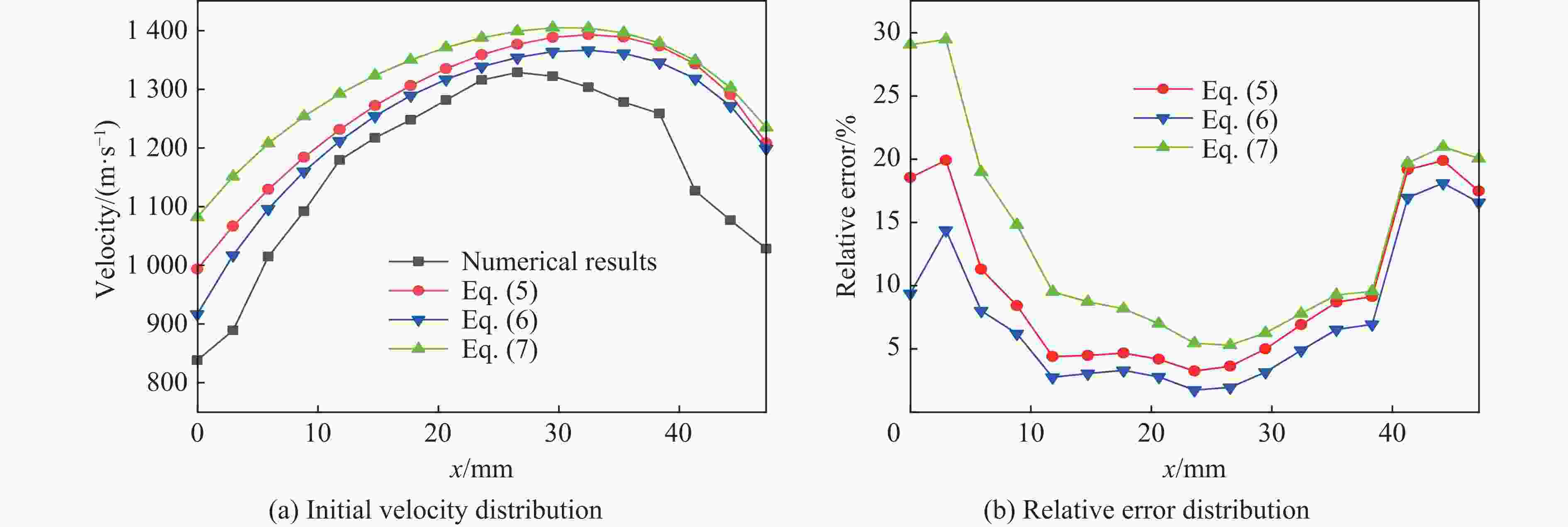
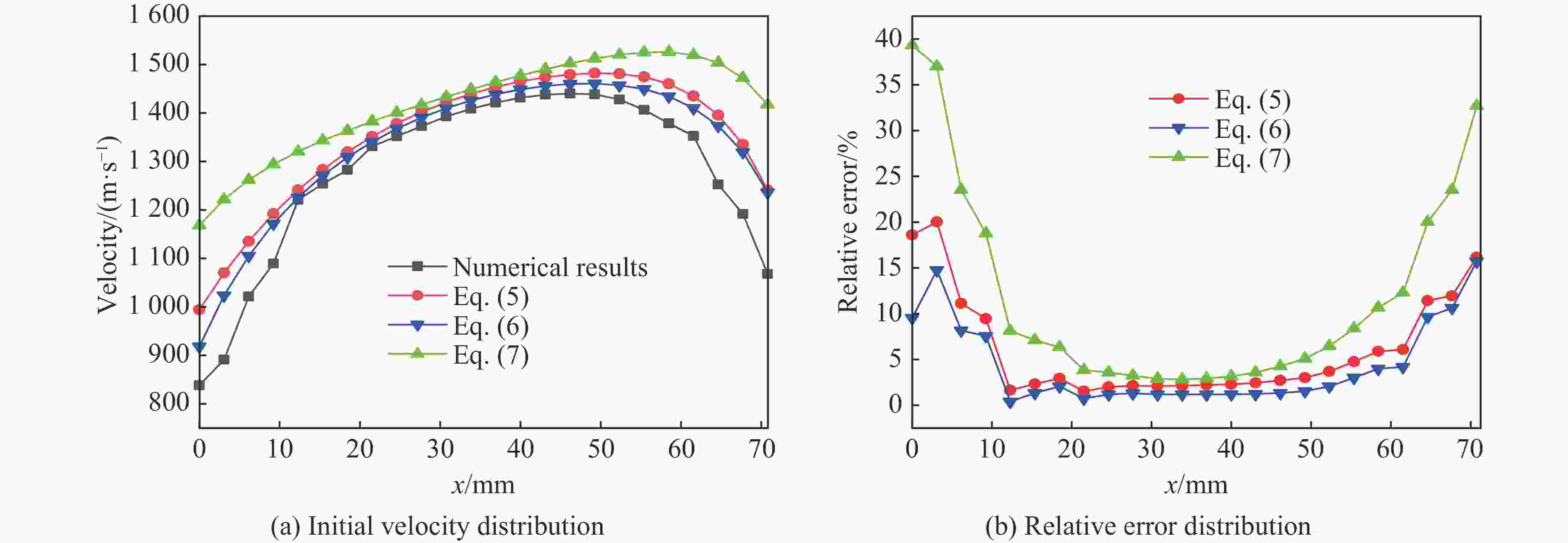
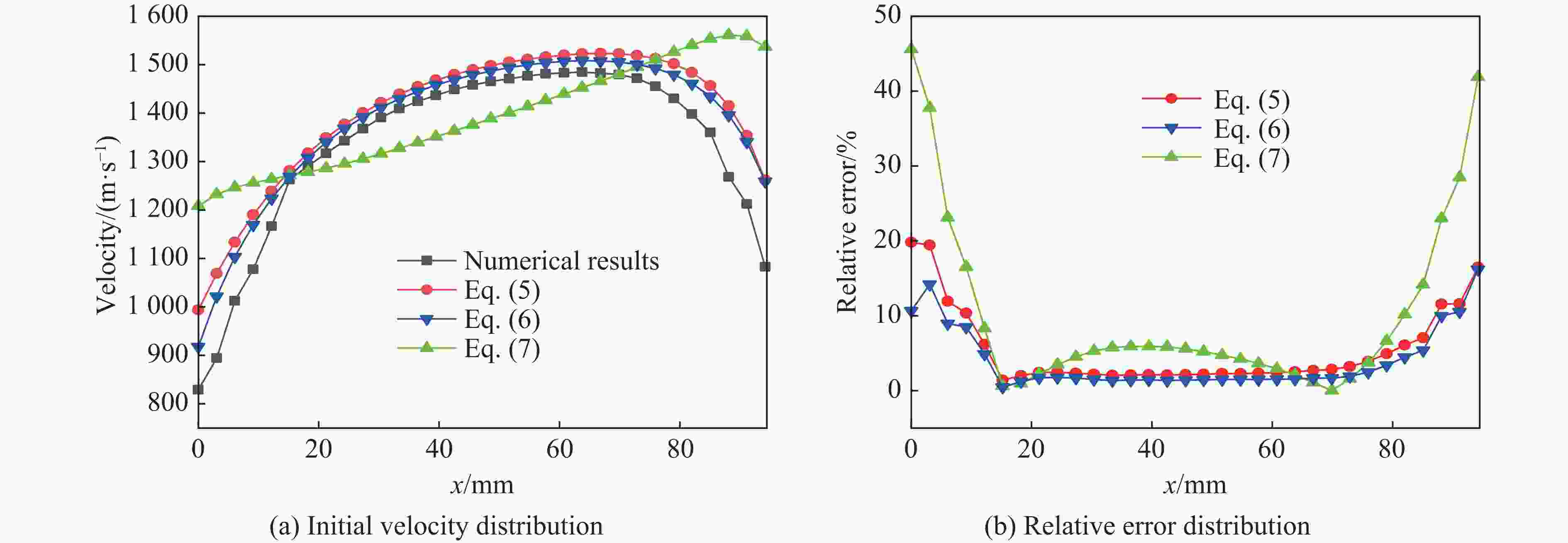
Axial distribution of fragment initial velocities from cylindrical casing with different length-to-diameter ratios

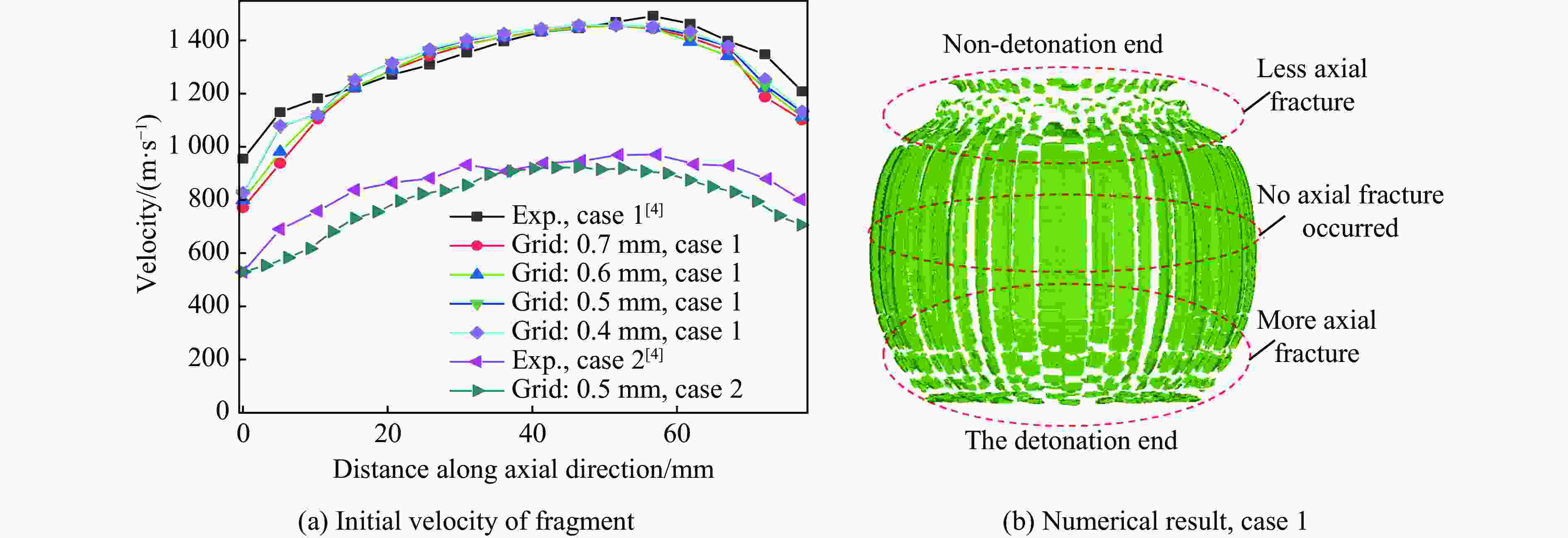
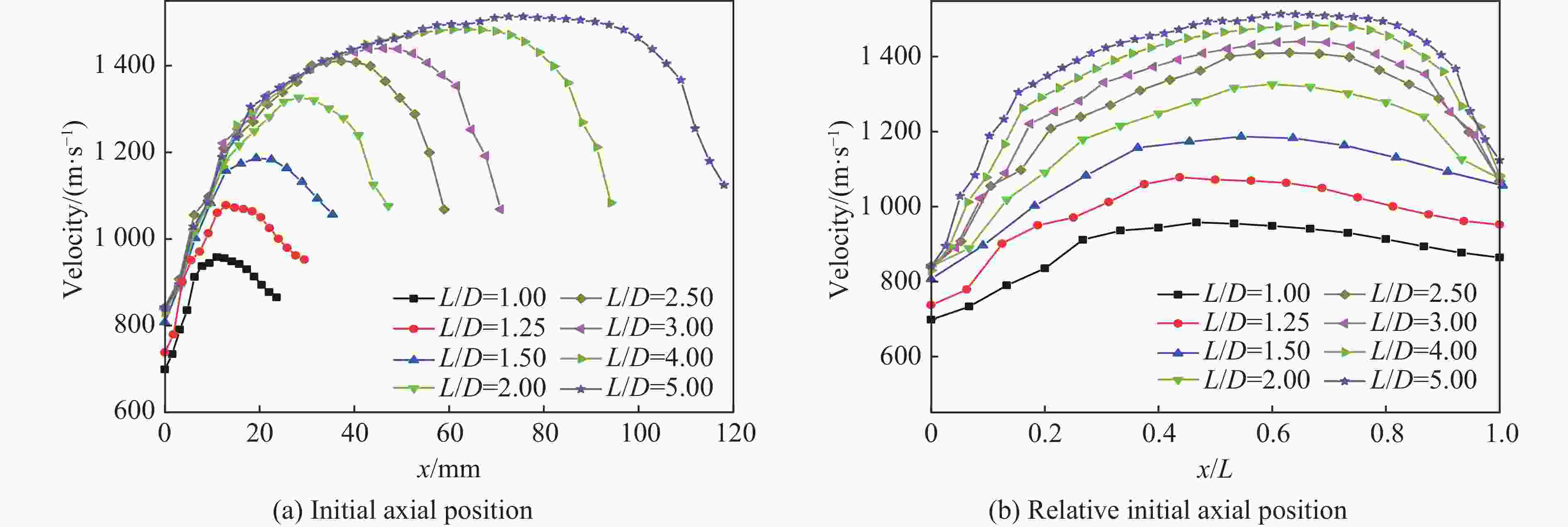
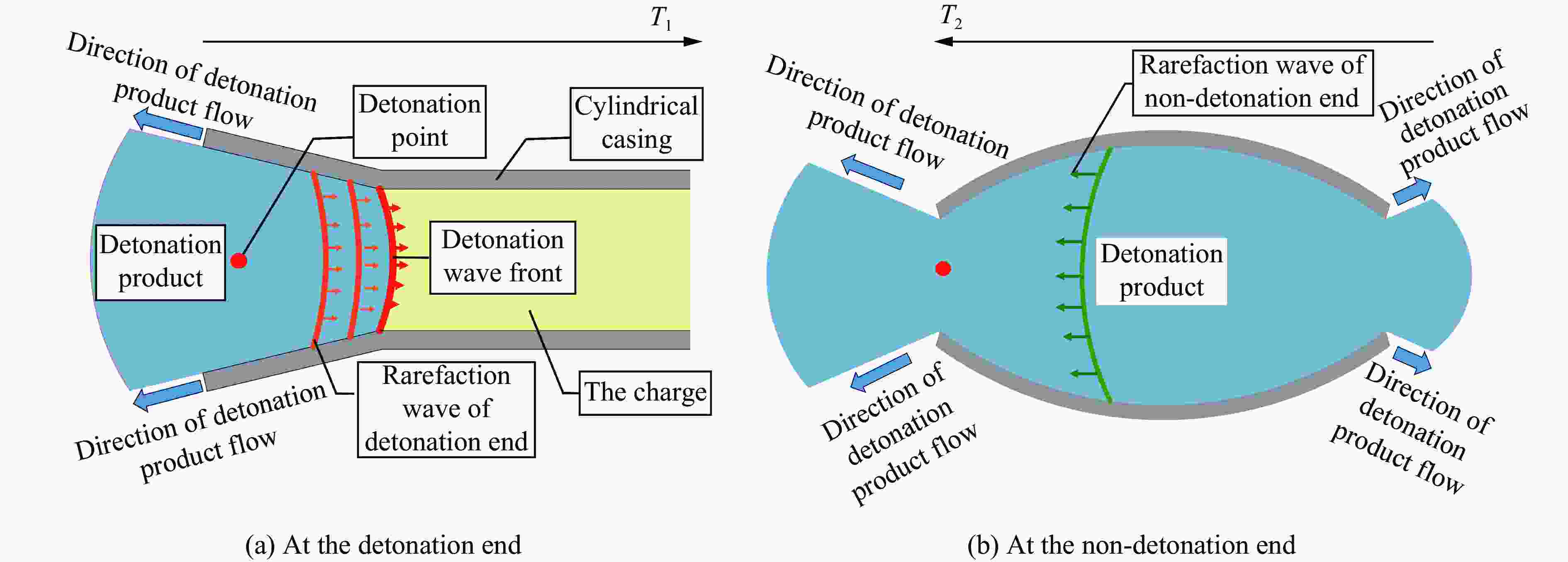
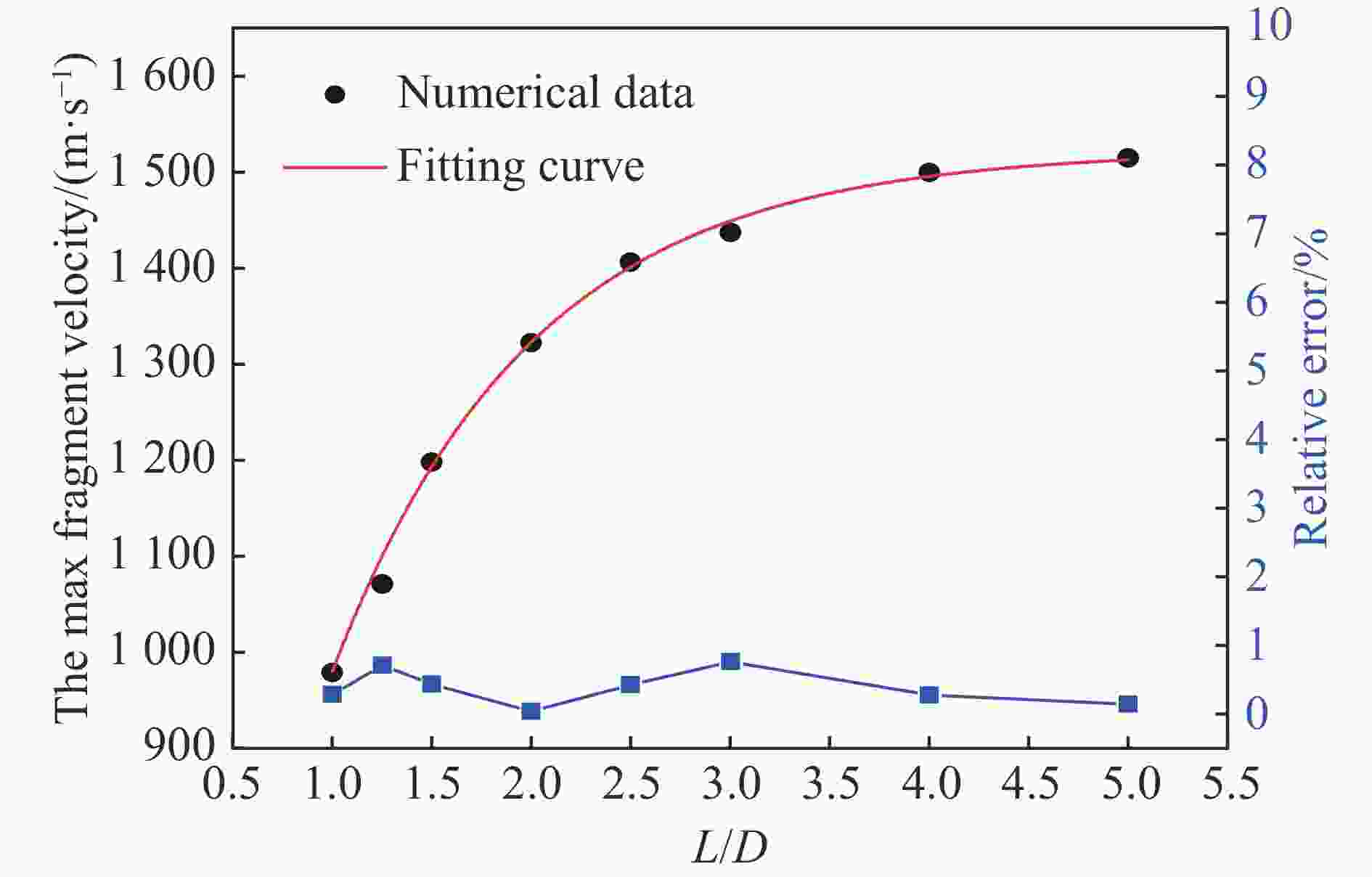
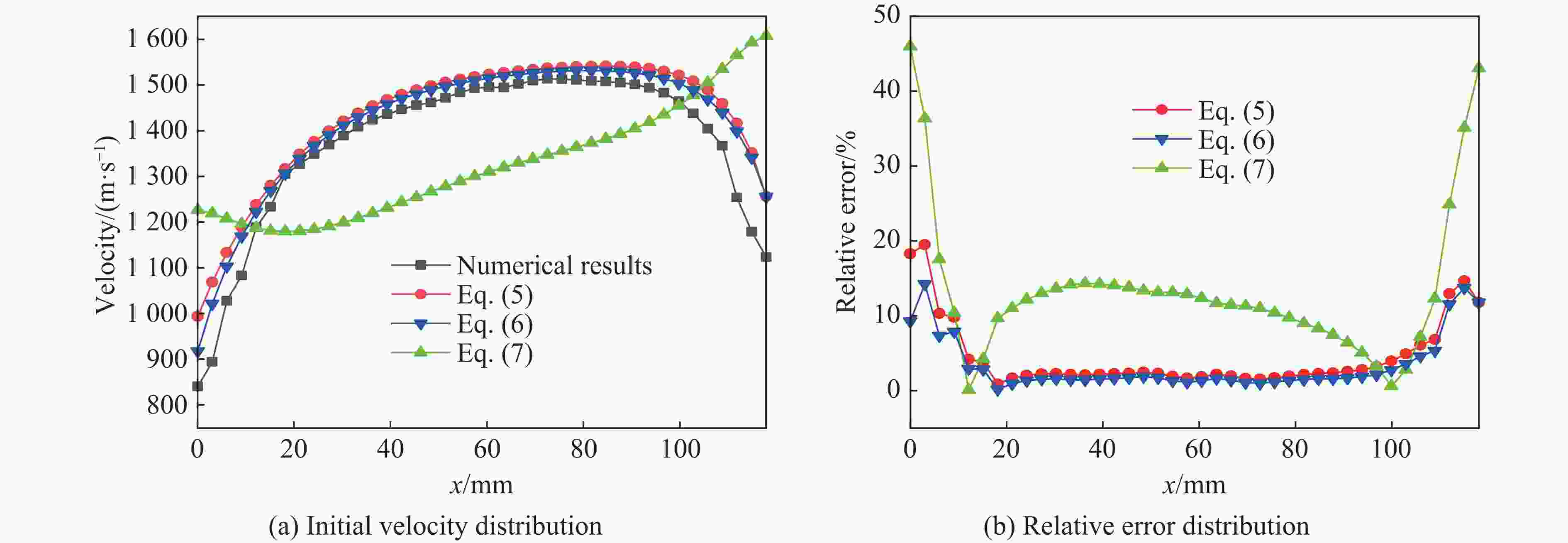
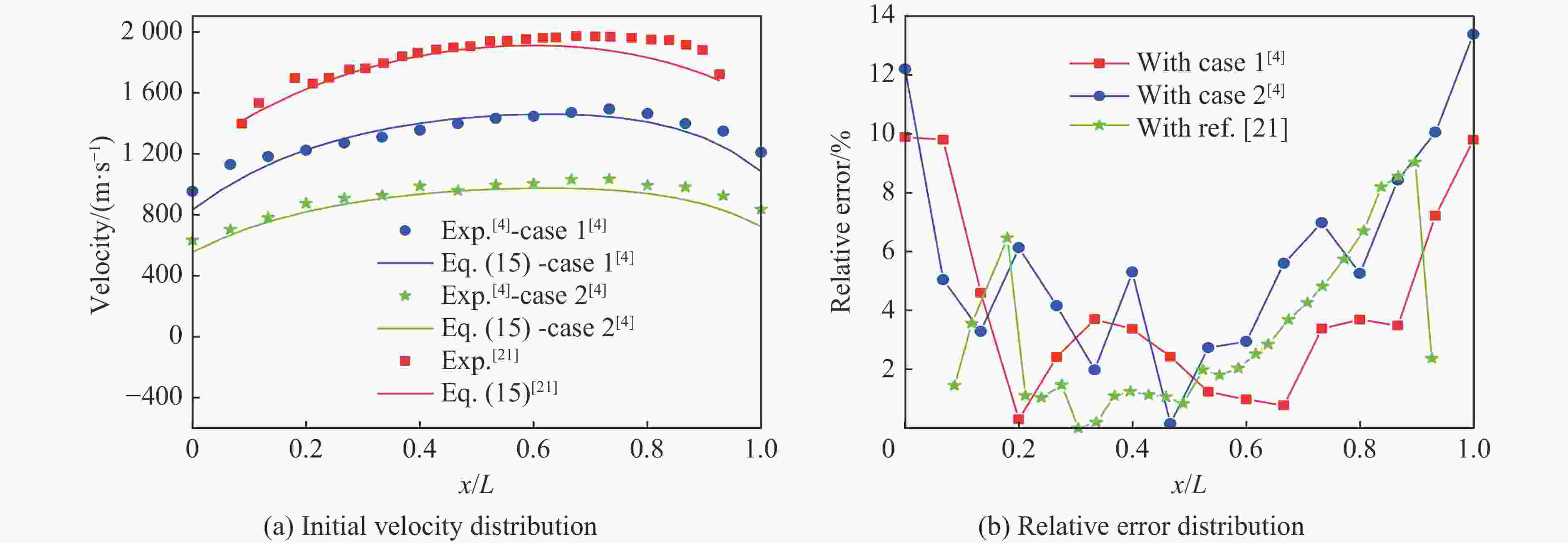
Ministerial Key Laboratory of ZNDY, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China

摘要

摘要: 针对精确预测不同长径比（L/D）的圆柱套筒在一段起爆下的破片初速分布问题，首先基于试验验证的数值模型研究了L/D对破片初速的影响；在此基础上，提出了适用于L/D≥1圆柱套筒的初速分布计算模型，该模型中添加了与L/D相关的受轴向稀疏波影响的修正项；最后，通过试验和数值模拟对所提出的初速计算模型进行了验证。研究结果表明：不同L/D下的破片初速分布均呈现两端初速低、中间高的变化趋势，且L/D越大，破片初速越高，当L/D达到5时，最大破片初速与Gurney公式计算结果之间的相对误差仅为0.15%；公式计算结果与试验结果和数值计算结果的平均误差不超过6%，表明该模型预测不同L/D下的破片初速分布是可靠的。
- 圆柱套筒 /
- 破片初速 /
- 长径比 /
- 轴向稀疏波
Abstract: To accurately predict the initial velocity distribution of cylindrical casing under central point detonation at one end with different length-diameter ratios (L/D), it studied the impact of L/D on the initial velocity of fragments and the applicability of existing empirical models for the initial velocity of fragments founded on the numerical model of experimental verification. On this basis, a correction term related to L/D, which was often influenced by the axial rarefaction waves, was added to the fragment initial velocity index model. By fitting the data obtained from numerical simulations, the function expression of the correction term was derived and the calculation model for the initial velocity distribution of cylindrical casing with L/D≥1 was obtained. Finally, the applicability of the established fragment initial velocity calculation model was validated through experimental data and numerical simulations. The research results indicate that the initial velocity distribution of fragments under different L/D exhibits a trend where the initial velocities are lower at both ends and higher in the middle. Additionally, as the L/D raises, the initial velocity of the fragment also increases. When the L/D reaches 5, the relative error between the maximum initial velocity of the fragments and the calculated result using the Gurney formula is only 1.99%. However, the existing models for calculating initial velocities of fragment display significant errors when predicting smaller L/D in cylindrical casing. The average error between the formula calculation results and the experimental and numerical simulation results does not exceed 6%, indicating that the proposed model is reliable for predicting the initial velocity distribution of fragments under different L/D.
- cylindrical casing /
- fragment initial velocity /
- length-to-diameter ratio /
- axial rarefaction wave

HTML全文

图 1 数值计算模型

Figure 1. Numerical calculation model

下载: 全尺寸图片幻灯片

图 2 数值模拟结果与试验结果^[4]的对比

Figure 2. Comparison of numerical results and experimental results^[4]

下载: 全尺寸图片幻灯片

图 3 不同L/D下破片初速分布

Figure 3. Fragment initial velocity distribution with different L/D

下载: 全尺寸图片幻灯片

图 4 稀疏波传播过程

Figure 4. Process of rarefaction wave propagation

下载: 全尺寸图片幻灯片

图 5 不同L/D下破片的最大初速

Figure 5. Maximum initial velocity of fragments for different L/D

下载: 全尺寸图片幻灯片

图 6 L/D=1时破片速度分布和相对误差分布对比情况

Figure 6. Comparison of fragment velocity distribution and relative error distribution while L/D=1

下载: 全尺寸图片幻灯片

图 7 L/D=2时破片速度分布和相对误差分布对比情况

Figure 7. Comparison of fragment velocity distribution and relative error distribution while L/D=2

下载: 全尺寸图片幻灯片

图 8 L/D=3时破片速度分布和相对误差分布对比情况

Figure 8. Comparison of fragment velocity distribution and relative error distribution while L/D=3

下载: 全尺寸图片幻灯片

图 9 L/D=4时破片速度分布和相对误差分布对比情况

Figure 9. Comparison of fragment velocity distribution and relative error distribution while L/D=4

下载: 全尺寸图片幻灯片

图 10 L/D=5时破片速度分布和相对误差分布对比情况

Figure 10. Comparison of fragment velocity distribution and relative error distribution while L/D=5

下载: 全尺寸图片幻灯片

图 11 系数A₁、B₁、C₁、D₁与L/D的关系

Figure 11. Relationship of coefficients A₁, B₁, C₁, D₁ with L/D

下载: 全尺寸图片幻灯片

图 12 试验结果和式(15)计算结果对比

Figure 12. Comparison of experimental results and calculation results of Eq. (15)

下载: 全尺寸图片幻灯片

图 13 仿真结果与式(15)计算结果对比（cases V1）

Figure 13. Comparison of numerical results and calculation results of Eq. (18) (cases V1)

下载: 全尺寸图片幻灯片

图 14 仿真结果与式(15)计算结果对比（cases V2）

Figure 14. Comparison of numerical results and calculation results of Eq. (18) (cases V2)

下载: 全尺寸图片幻灯片

图 15 仿真结果与式(15)计算结果对比（cases V3）

Figure 15. Comparison of numerical results and calculation results of Eq. (18) (cases V3)

下载: 全尺寸图片幻灯片

表 1 不同$L/D $的数值模拟试样

Table 1. Simulation samples with different L/D

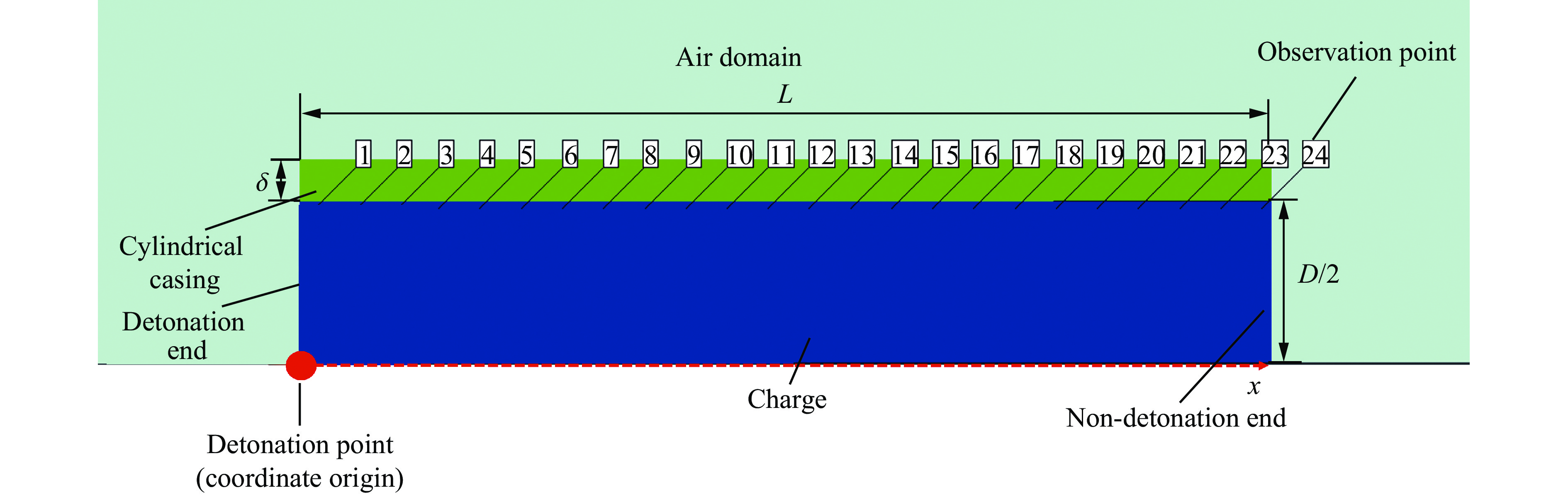
模型	D/mm	L/mm	L/D	δ/mm	模型	D/mm	L/mm	L/D	δ/mm
1	23.6	23.6	1.00	3.04	5	23.6	59.0	2.50	3.04
2	23.6	29.5	1.25	3.04	6	23.6	70.8	3.00	3.04
3	23.6	35.4	1.50	3.04	7	23.6	94.4	4.00	3.04
4	23.6	47.2	2.00	3.04	8	23.6	118.0	5.00	3.04

下载: 导出CSV

表 2 AISI1045的J-C本构模型参数^[14-15]

Table 2. J-C constitutive model parameters of AISI1045^[14-15]

密度/(g·cm⁻³)	A_JC/MPa	B_JC/MPa	n	C_JC	m	D₁	D₂	D₃	D₄	D₅
7.83	507	320	0.28	0.064	1.06	0.15	0.72	1.66	0.005	−0.84

下载: 导出CSV

表 3 B炸药的材料参数^[4]

Table 3. Material parameters of Comp B^[4]

爆速/(m·s⁻¹)	爆轰压力/GPa	E/(kJ·m⁻³)	A_JWL/GPa	B_JWL/GPa	R₁	R₂	ω
7980	29	8.5×10⁶	542	7.68	4.2	1.1	0.24

下载: 导出CSV

表 4 Huang的试验样本参数^[4]

Table 4. Parameters of Huang's test sample ^[4]

工况	套筒材料	装药材料	D/mm	L/mm	δ/mm
1	ASI1045	B炸药	23.60	77.30	3.04
2	ASI1045	B炸药	23.56	77.15	6.69

下载: 导出CSV

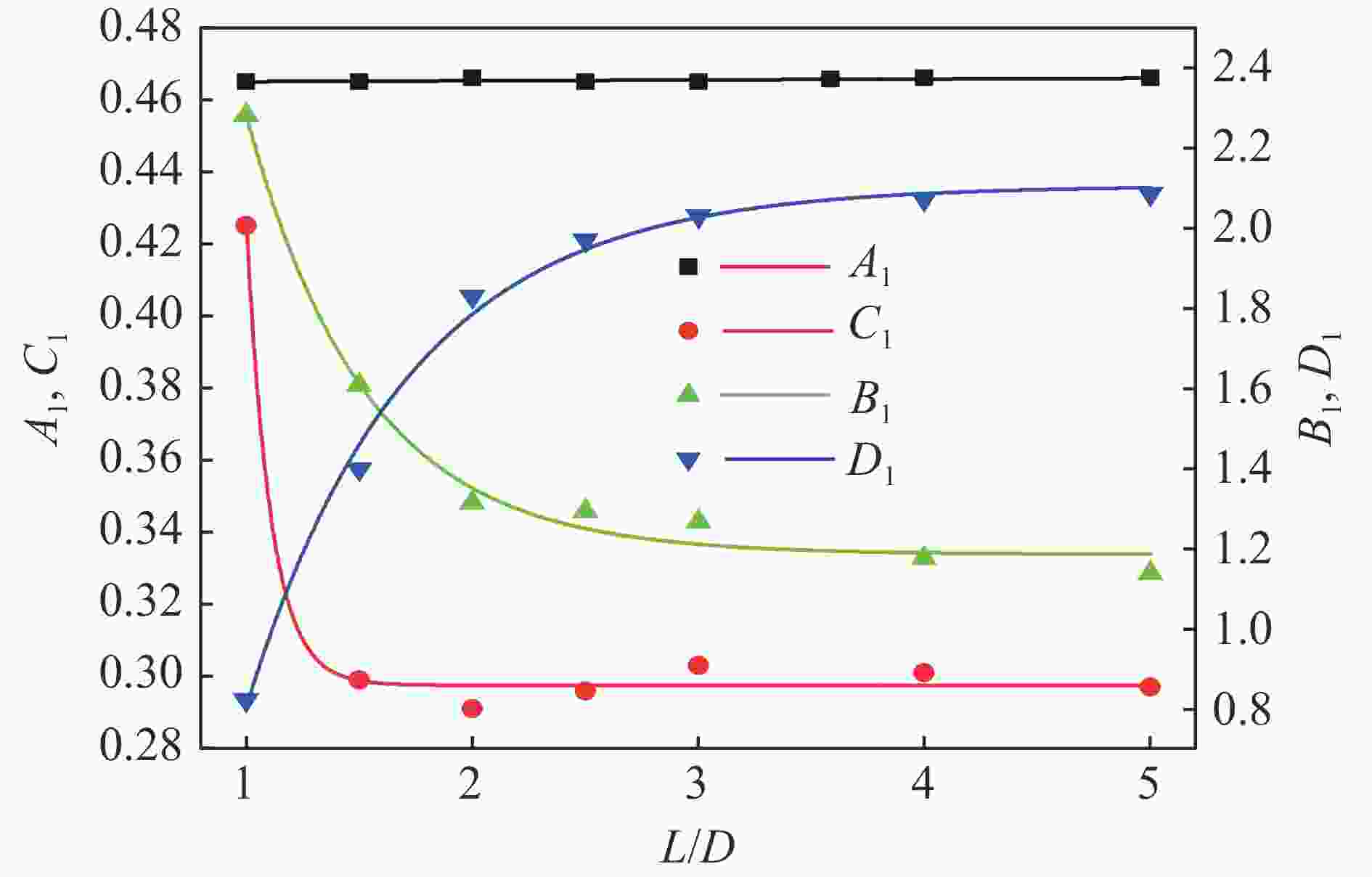
表 5 不同$L/D $下的的$A_1 $、$B_1 $、$C_1 $、$D_1 $系数

Table 5. Coefficients A₁, B₁, C₁ and D₁ obtained with different L/D

L/D	A₁	B₁	C₁	D₁	L/D	A₁	B₁	C₁	D₁
1.00	0.465	2.282	0.425	0.823	2.50	0.465	1.293	0.296	1.970
1.25	0.465	1.983	0.326	1.121	3.00	0.465	1.267	0.303	2.030
1.50	0.465	1.607	0.299	1.399	4.00	0.466	1.175	0.301	2.072
2.00	0.466	1.314	0.291	1.830	5.00	0.466	1.137	0.297	2.086

下载: 导出CSV

表 6 9个用于验证公式的试样参数

Table 6. Nine sample parameters used to validate the formula

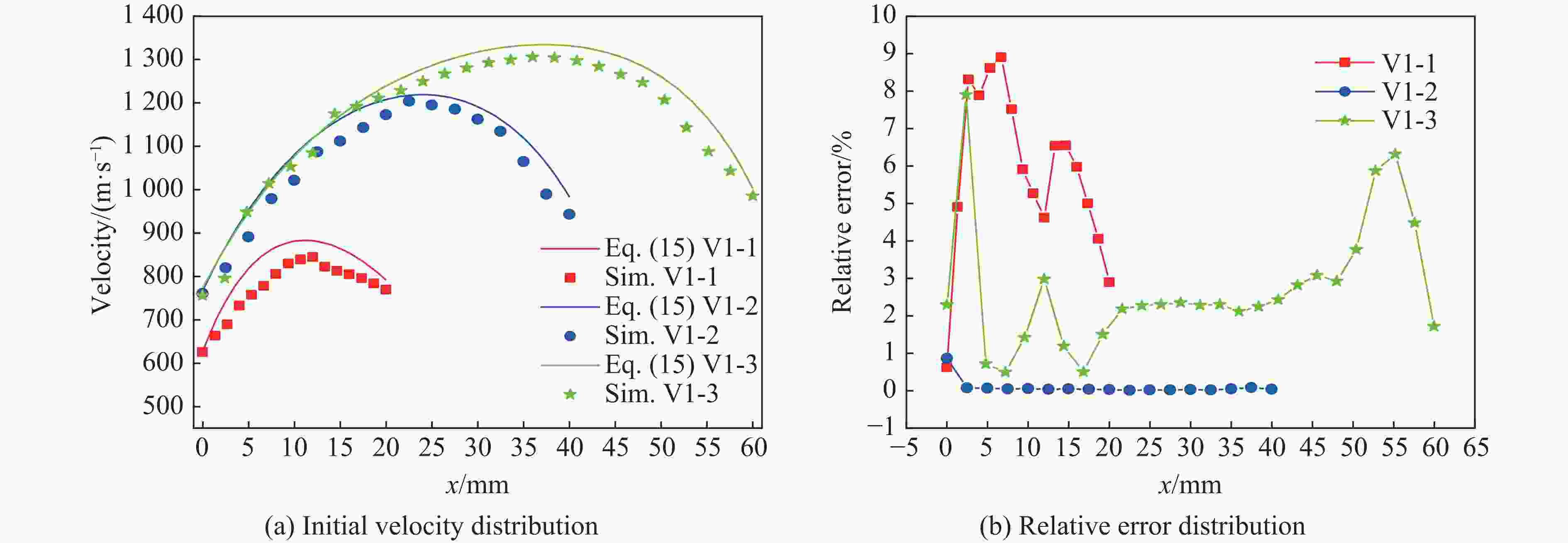
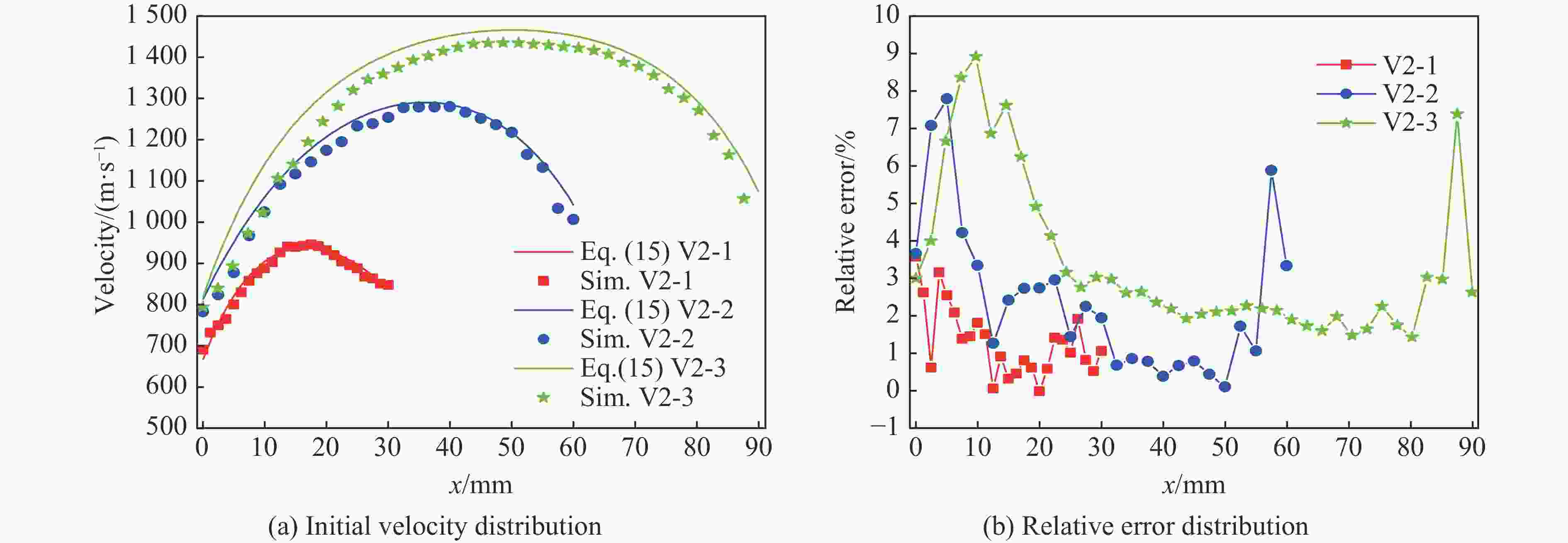
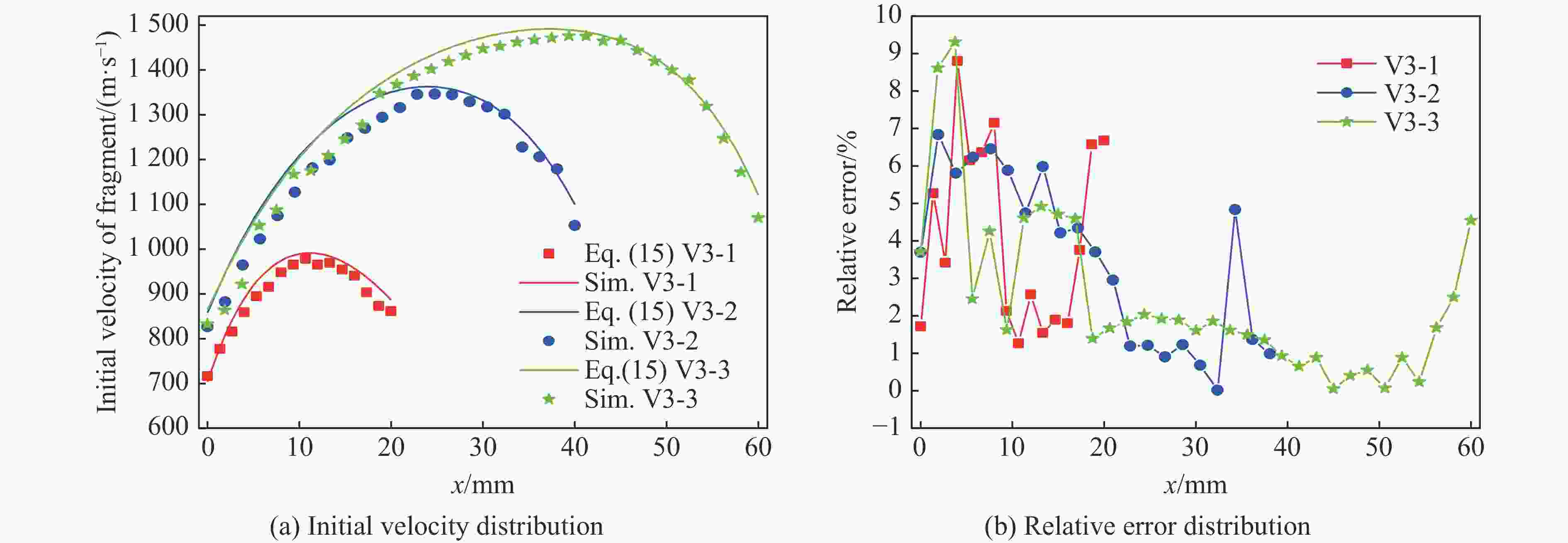
工况	装药	D/mm	L/mm	D/L	δ/mm	工况	装药	D/mm	L/mm	D/L	δ/mm	工况	装药	D/mm	L/mm	D/L	δ/mm
V1-1	B炸药	20	20	1.0	3.0	V2-1	B炸药	30	30	1.0	4.0	V3-1	HMX	20	20	1.0	3.0
V1-2	B炸药	20	40	1.2	3.0	V2-2	B炸药	30	60	1.2	4.0	V3-2	HMX	20	40	1.2	3.0
V1-3	B炸药	20	60	3.0	3.0	V2-3	B炸药	30	90	3.0	4.0	V3-3	HMX	20	60	3.0	3.0
注：所有工况中套筒材料均为ASI1045.

下载: 导出CSV

表 7 HMX的材料参数^[22]

Table 7. The material parameters of HMX^[22]

爆速/(m·s⁻¹)	爆轰压力/GPa	E/(kJ·m⁻³)	A_JWL/GPa	B_JWL/GPa	R₁	R₂	ω
9110	42.0	10.5×10⁶	778.28	7.07	4.2	1.0	0.30

下载: 导出CSV

参考文献(22)

[1]	GURNEY R W. The initial velocities of fragments from bombs, shell, and grenades [M]. Aberdeen: Ballistic Research Laboratories, 1943.
[2]	ZULKOSKI T. Development of optimum theoretical warhead design criteria [R]. China Lake: Naval Weapons Center, 1976.
[3]	CHARRON Y J. Estimation of velocity distribution of fragmenting warheads using a modified Gurney method [M]. PN, 1979.
[4]	HUANG G Y, LI W, FENG S S. Axial distribution of fragment velocities from cylindrical casing under explosive loading [J]. International Journal of Impact Engineering, 2015, 76: 20–27. DOI: 10.1016/j.ijimpeng.2014.08.007.
[5]	GAO Y G, ZHANG B, YAN X M, et al. Axial distribution of fragment velocities from cylindrical casing with air parts at two ends [J]. International Journal of Impact Engineering, 2020, 140: 103535. DOI: 10.1016/j.ijimpeng.2020.103535.
[6]	LIU H, HUANG G Y, GUO Z W, et al. Fragments velocity distribution and estimating method of thin-walled cylindrical improvised explosive devices with different length-to-diameter ratios [J]. Thin-Walled Structures, 2022, 175: 109212. DOI: 10.1016/j.tws.2022.109212.
[7]	BI W X, LI W B, LUO Y S, et al. Pre-control of shell expansion fracture process by high energy beam [J]. Journal of Physics: Conference Series, 2023, 2478: 072002. DOI: 10.1088/1742-6596/2478/7/072002.
[8]	XU H Y, LI W B, LI W B, et al. Fracture mechanism of a cylindrical shell cut by circumferential detonation collision [J]. Defence Technology, 2021, 17(5): 1650–1659. DOI: 10.1016/j.dt.2020.09.006.
[9]	李元, 李燕华, 刘琛, 等. 预制破片战斗部爆轰产物泄露数值模拟 [J]. 北京理工大学学报, 2017, 37(8): 778–782. DOI: 10.15918/j.tbit1001-0645.2017.08.002. LI Y, LI Y H, LIU C, et al. Modeling of the gas leakage of premade fragment warhead [J]. Transactions of Beijing Institute of Technology, 2017, 37(8): 778–782. DOI: 10.15918/j.tbit1001-0645.2017.08.002.
[10]	LI W, HUANG G Y, FENG S S. Effect of eccentric edge initiation on the fragment velocity distribution of a cylindrical casing filled with charge [J]. International Journal of Impact Engineering, 2015, 80: 107–115. DOI: 10.1016/j.ijimpeng.2015.01.007.
[11]	XU W L, WANG C, CHEN D P. Formation of a bore-center annular shaped charge and its penetration into steel targets [J]. International Journal of Impact Engineering, 2019, 127: 122–134. DOI: 10.1016/j.ijimpeng.2019.01.008.
[12]	BHATTACHARYA A K, NIX W D. Finite element simulation of indentation experiments [J]. International Journal of Solids and Structures, 1988, 24(9): 881–891. DOI: 10.1016/0020-7683(88)90039-X.
[13]	JOHNSON G R, COOK W H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures [J]. Engineering Fracture Mechanics, 1985, 21(1): 31–48. DOI: 10.1016/0013-7944(85)90052-9.
[14]	陈刚, 陈忠富, 陶俊林, 等. 45钢动态塑性本构参量与验证 [J]. 爆炸与冲击, 2005, 25(5): 451–456. DOI: 10.11883/1001-1455(2005)05-0451-06. CHEN G, CHEN Z F, TAO J L, et al. Investigation and validation on plastic constitutive parameters of 45 steel [J]. Explosion and Shock Waves, 2005, 25(5): 451–456. DOI: 10.11883/1001-1455(2005)05-0451-06.
[15]	陈刚, 陈忠富, 徐伟芳, 等. 45钢的J-C损伤失效参量研究 [J]. 爆炸与冲击, 2007, 27(2): 131–135. DOI: 10.11883/1001-1455(2007)02-0131-05. CHEN G, CHEN Z F, XU W F, et al. Investigation on the J-C ductile fracture parameters of 45 steel [J]. Explosion and Shock Waves, 2007, 27(2): 131–135. DOI: 10.11883/1001-1455(2007)02-0131-05.
[16]	SOUERS P C, HASELMAN JR L C. Detonation equation of state at LLNL, 1993: UCRL-ID-116113 [R]. Livermore: Lawrence Livermore National Laboratory, 1994. DOI: 10.2172/10166640.
[17]	LI W B, WANG X M, LI W B. The effect of annular multi-point initiation on the formation and penetration of an explosively formed penetrator [J]. International Journal of Impact Engineering, 2010, 37(4): 414–424. DOI: 10.1016/j.ijimpeng.2009.08.008.
[18]	张守中. 爆炸与冲击动力学 [M]. 北京: 兵器工业出版社, 1993. ZHANG S Z. Explosion and impact dynamics [M]. Beijing: CNGC, 1993.
[19]	DANEL J F, KAZANDJIAN L. A few remarks about the Gurney energy of condensed explosives [J]. Propellants, Explosives, Pyrotechnics, 2004, 29(5): 314–316. DOI: 10.1002/prep.200400060.
[20]	高月光, 冯顺山, 刘云辉, 等. 不同端盖厚度的圆柱形装药壳体破片初速分布 [J]. 兵工学报, 2022, 43(7): 1527–1536. DOI: 10.12382/bgxb.2021.0443. GAO Y G, FENG S S, LIU Y H, et al. Initial velocity distribution of fragments from cylindrical charge shells with different thick end caps [J]. Acta Armamentarii, 2022, 43(7): 1527–1536. DOI: 10.12382/bgxb.2021.0443.
[21]	ANDERSON JR C E, PREDEBON W W, KARPP R R. Computational modeling of explosive-filled cylinders [J]. International Journal of Engineering Science, 1985, 23(12): 1317–1330. DOI: 10.1016/0020-7225(85)90110-7.
[22]	DOBRATZ B M. LLNL explosives handbook: properties of chemical explosives and explosives and explosive simulants: UCRL-52997 [R]. Livermore: Lawrence Livermore National Laboratory. DOI: 10.2172/6530310.