冲击质量对方形锂离子电池在冲击载荷下动态力学响应和失效模式的影响

王涛; 孟康培; 刘跃专; 袁泉; 黄浩; 陈晓平

doi:10.11883/bzycj-2024-0316

冲击质量对方形锂离子电池在冲击载荷下动态力学响应和失效模式的影响

doi: 10.11883/bzycj-2024-0316

王涛^1,,
孟康培¹,
刘跃专¹,
袁泉¹,
黄浩²,
陈晓平^1, ,

1.
宁波工程学院机械与汽车工程学院，浙江宁波 315016
2.
长安大学能源与电气工程学院，陕西西安 710064

基金项目: 国家自然科学基金（12402457）；宁波市自然科学基金（2023J389）

详细信息

作者简介:
王　涛（1978－　），男，硕士，高级实验师，wangtao@nbut.edu.cn

通讯作者:
陈晓平（1978－　），男，博士，教授，cxp@nbut.edu.cn

中图分类号: O347
计量
- 文章访问数: 84
- HTML全文浏览量: 31
- PDF下载量: 32
- 被引次数: 0
出版历程
- 收稿日期: 2024-08-29
- 修回日期: 2024-12-20
- 网络出版日期: 2024-12-25
- 刊出日期: 2025-02-01

Effects of impact mass on dynamic mechanical responses and failure modes of square lithium-ion batteries under impact loading

1.
Department of Mechanical Engineering, Ningbo University of Technology, Ningbo 315016, Zhejiang, China
2.
School of Energy and Electrical Engineering, Changʼan University, Xiʼan 710064, Shaanxi, China

摘要

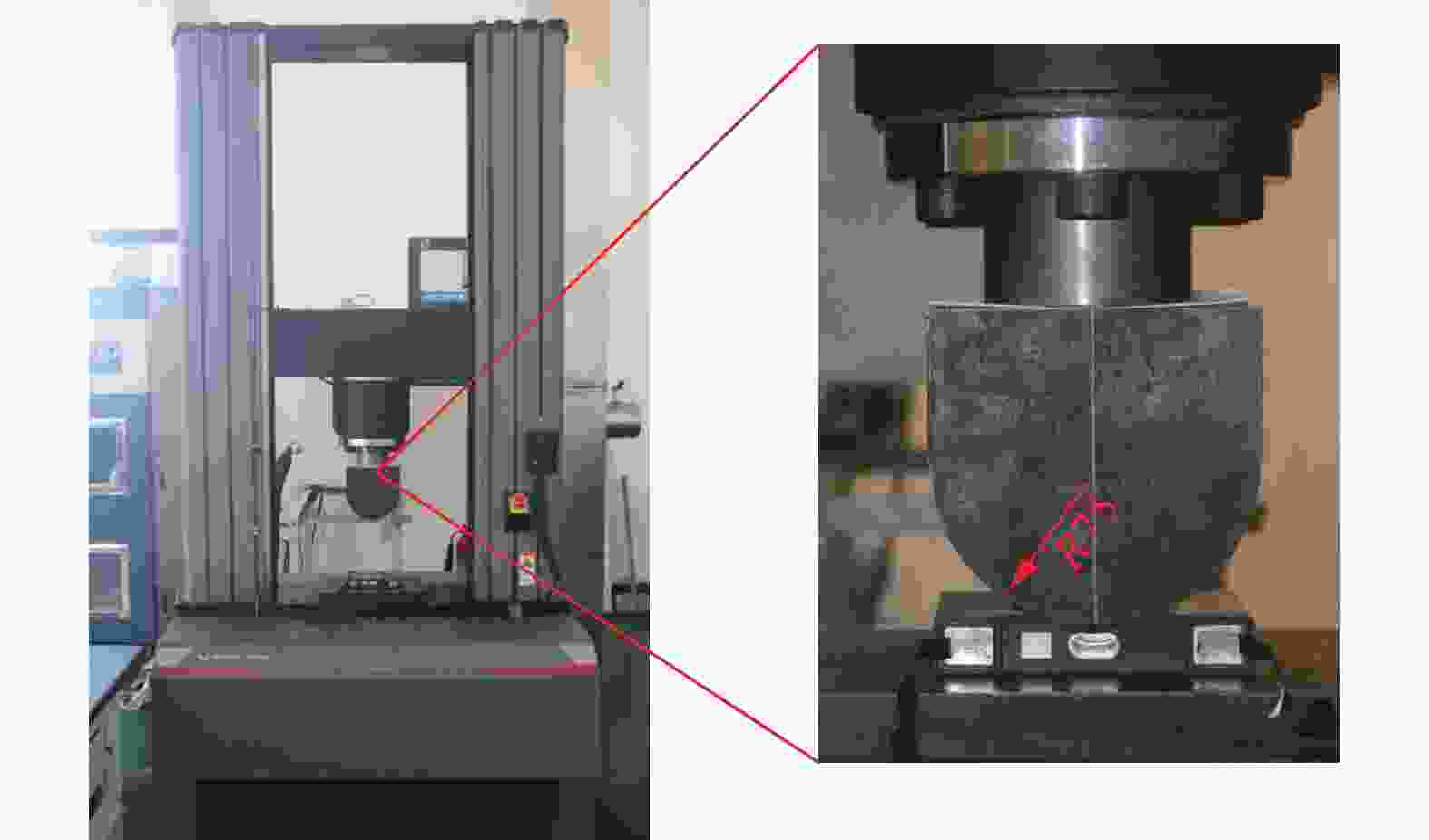
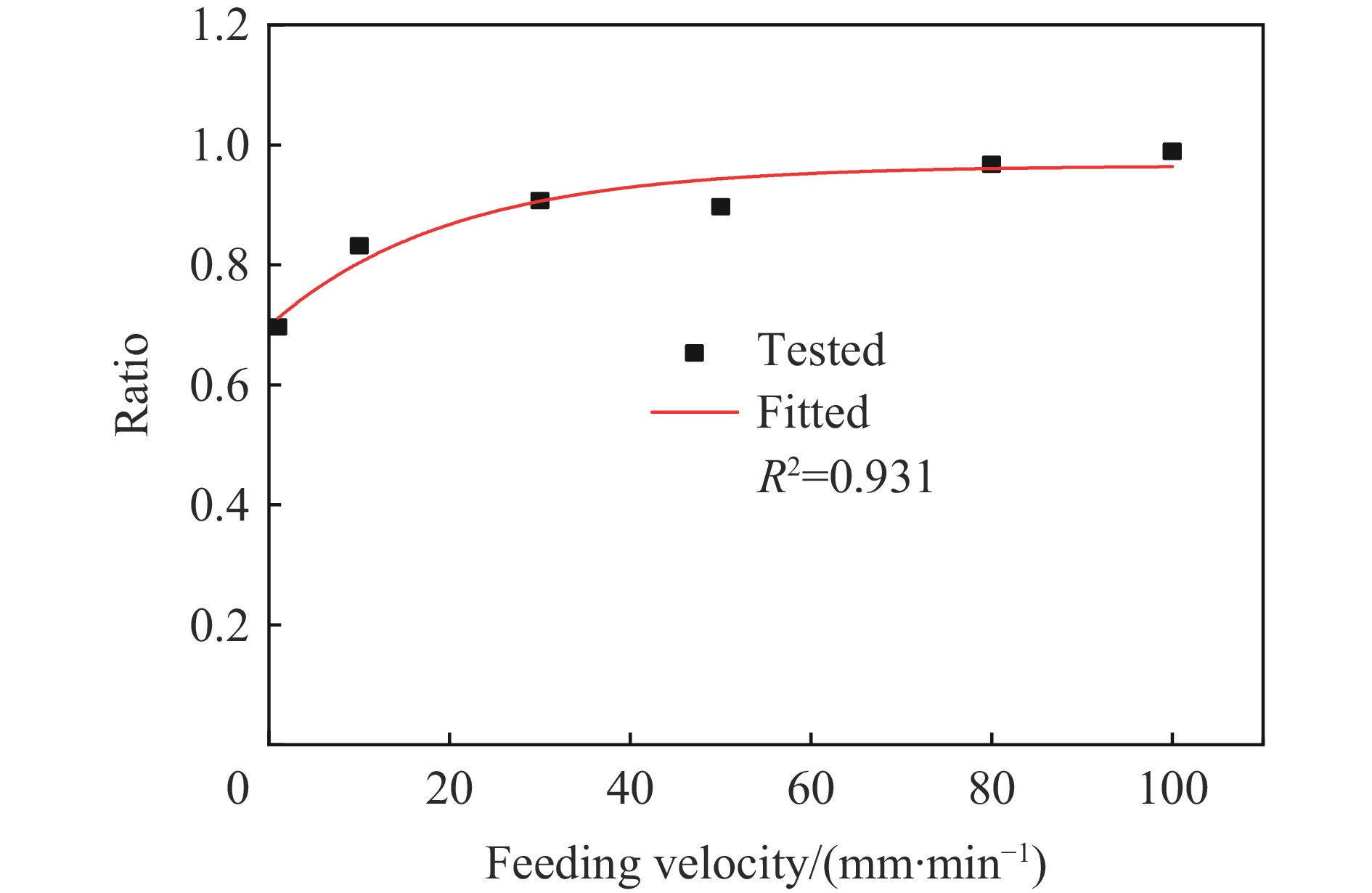
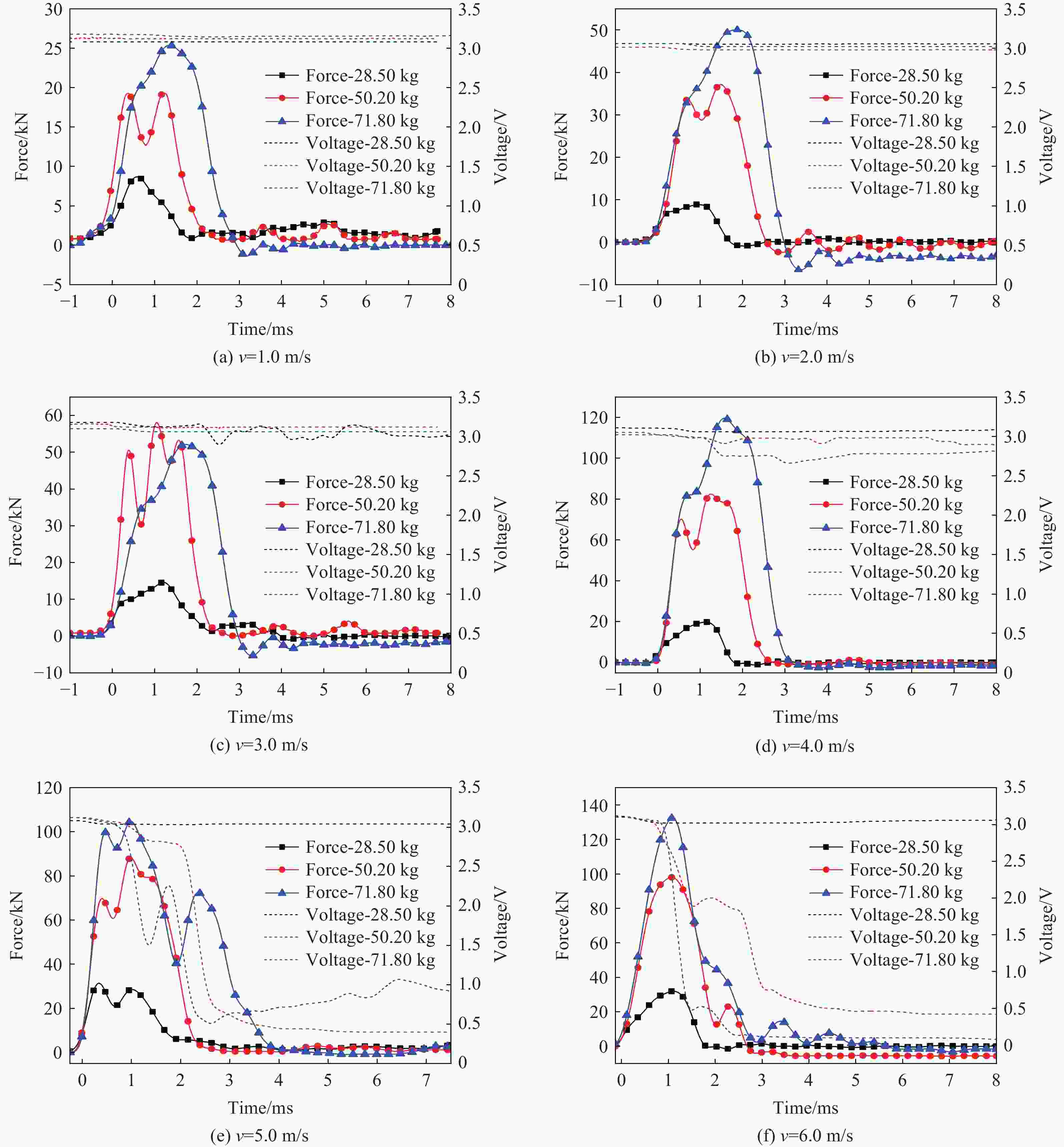
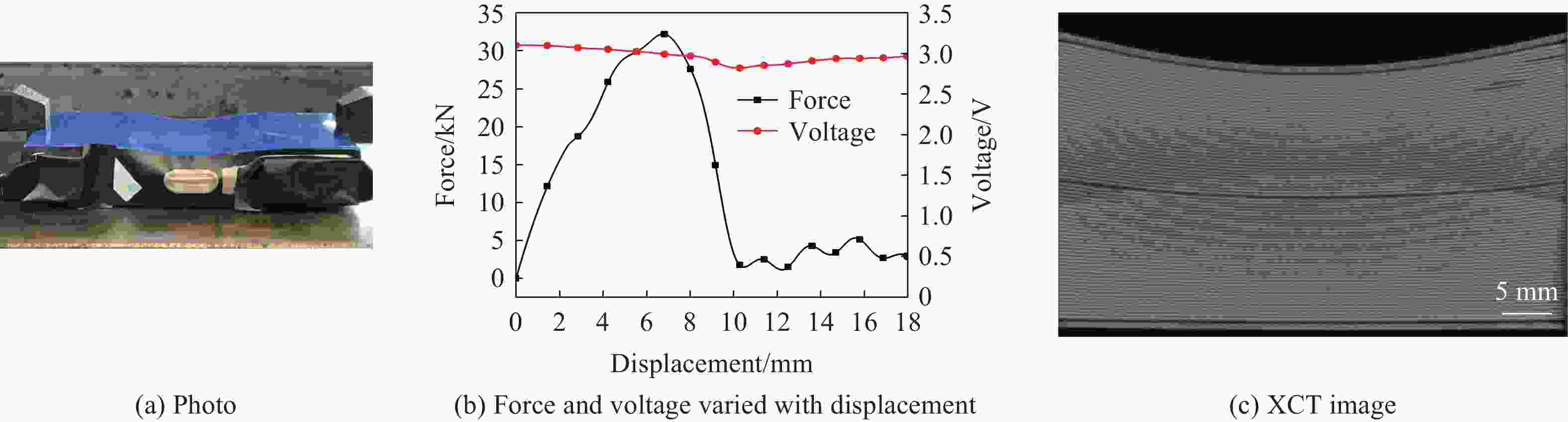
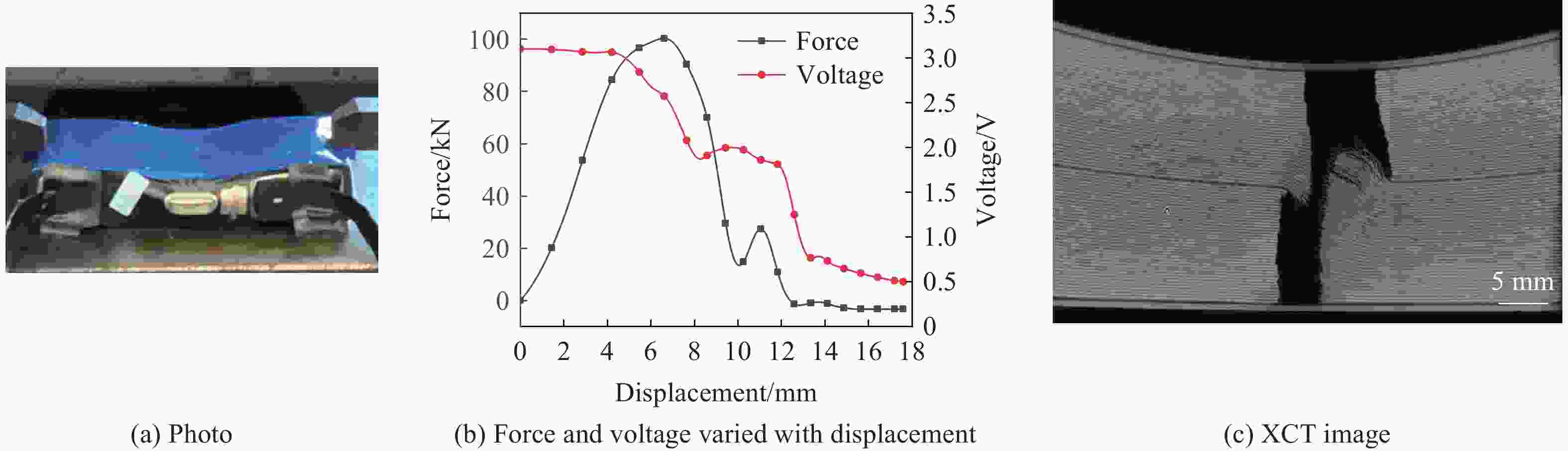
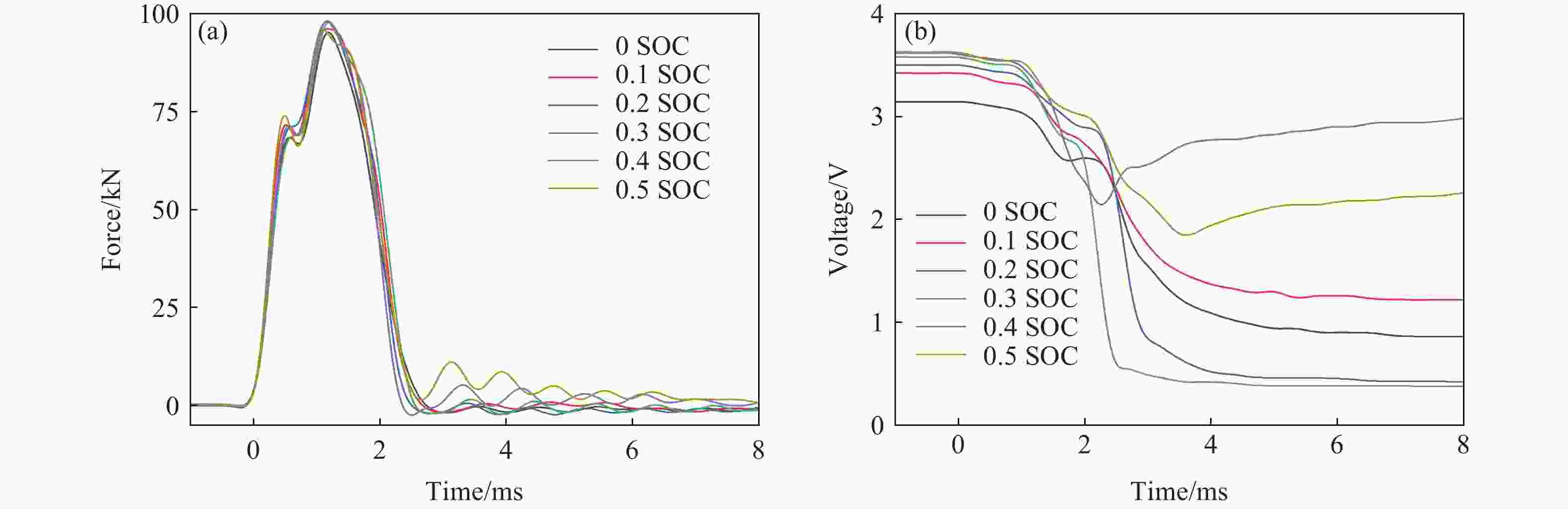
摘要: 电动汽车在运行过程中容易发生碰撞事故，动力锂离子电池不可避免会受到冲击作用，导致电池不同程度的损伤，而损伤程度的判断对电池的安全使用至关重要。基于上述背景，开展了不同冲击质量对方形锂离子电池动态冲击响应和失效行为影响的研究。首先，开展了准静态压缩试验，采用6种不同的进给速度对锂离子电池进行了挤压测试。试验结果显示，随着进给速度的递增，锂离子电池达到硬短路失效所需的峰值载荷持续减小。这表明，准静态条件下，锂离子电池的短路失效载荷主要由挤压速度决定。然后，开展了落锤冲击试验，通过调控冲头的质量和冲击速度，系统模拟了锂离子电池可能遭遇的多种冲击工况。研究结果表明，冲击质量和冲击速度是决定锂离子电池动态失效行为的关键因素。在冲击能量恒定的条件下，相较于高速、小质量的冲击条件，低速、大质量的冲头冲击对电芯内部造成的损伤更明显；当冲头质量不变时，提高冲击速度则会提前触发锂离子电池的内短路。
- 方形锂离子电池 /
- 冲击质量 /
- 冲击速度 /
- 冲击能量 /
- 动态失效
Abstract: Electric vehicles are prone to collision accidents during operation, and power lithium-ion batteries are inevitably subjected to impact, which leads to varying degrees of damage to the battery, and assessing the extent of this damage is crucial for the safe use of the battery. Based on the above background, the study was conducted on the influence of different impact masses on the dynamic impact response and failure behavior of square lithium-ion batteries. Firstly, in the quasi-static compression test, six different feed rates were used to test the extrusion of lithium-ion batteries. The test results show that the peak load required for lithium-ion batteries to reach hard short-circuit failure continues to decrease with the increment of feed rate. This indicates that the short-circuit failure load of lithium-ion batteries under quasi-static conditions is mainly determined by the feed rate. Then the hammer impact test, through the regulation of the quality of the punch and impact speed, the system simulates the lithium-ion battery may encounter a variety of impact conditions. Impact quality is an important factor in determining the degree of damage to lithium-ion batteries. Under the same impact energy, the damage of low-speed large mass impact on lithium-ion battery is significantly higher than that of high-speed low mass impact. At a constant impact energy, mass is the dominant factor in determining the degree of battery damage. If the impact mass is heavier, it will produce a larger impact load, which will cause more serious damage to the internal structure of the lithium-ion battery, leading to its functional damage or even failure. Conversely, if the impact mass is lighter, the impact force generated is relatively small, and the damage to the battery structure is correspondingly reduced. Therefore, the size of the impact mass directly affects the degree of damage to the lithium-ion battery, which is a key indicator for evaluating its safety performance and durability. The impact speed has a significant impact on the voltage drop of lithium-ion batteries after damage. Especially accelerating the occurrence of hard short circuits, further exacerbating the sharp drop in voltage. This characteristic makes the impact velocity as an important consideration for evaluating the voltage stability and overall safety performance of lithium-ion batteries after damage.
- square lithium-ion battery /
- impact mass /
- impact velocity /
- impact energy /
- dynamic failure

HTML全文

图 1 用于测试的方形锂离子电池

Figure 1. A square lithium-ion battery used for testing

下载: 全尺寸图片幻灯片

图 2 Instron2386万能试验机

Figure 2. Instron2386 universal testing machine

下载: 全尺寸图片幻灯片

图 3 落重测试系统

Figure 3. Drop-weight test system

下载: 全尺寸图片幻灯片

图 4 不同进给速度对锂离子电池短路失效的影响

Figure 4. Influences of different feeding velocities on short-circuit failure of lithium-ion batteries

下载: 全尺寸图片幻灯片

图 5 硬短路失效点能量-进给速度拟合曲线

Figure 5. Fitted energy-feeding velocity curve of hard short circuit failure points

下载: 全尺寸图片幻灯片

图 6 图4中第2个波峰载荷与第1个波峰载荷之比随进给速度的变化

Figure 6. Ratio of the force at the second wave crest to the one at the first wave crest in Fig.4 varied with feeding velocity

下载: 全尺寸图片幻灯片

图 7 不同冲击速度和冲头质量的冲击试验中锂离子电池所受到的冲击力及其电压随时间的变化

Figure 7. Variation of impact force loaded on a lithium-ion battery and its voltage with time in drop-weight impact tests with different impact velocities and punch head masses

下载: 全尺寸图片幻灯片

图 8 在质量为28.50 kg的冲头以6.0 m/s的速度冲击下锂离子电池的结构及其受到的冲击力和电压随位移的变化

Figure 8. Battery structures as well as variations of impact forces loaded on batteries and their voltages with displacement under impact of a 28.50-kg punch head at the impact velocity of 6.0 m/s

下载: 全尺寸图片幻灯片

图 9 在质量为50.20 kg的冲头以6.0 m/s的速度冲击下锂离子电池的结构及其受到的冲击力和电压随位移的变化

Figure 9. Battery structures as well as variations of impact forces loaded on batteries and their voltages with displacement under impact of a 50.20-kg punch head at the impact velocity of 6.0 m/s

下载: 全尺寸图片幻灯片

图 10 在质量为71.80 kg的冲头以6.0 m/s的速度冲击下锂离子电池的结构及其受到的冲击力和电压随位移的变化

Figure 10. Battery structures as well as variations of impact forces loaded on batteries and their voltages with displacement under impact of a 71.80-kg punch head at the impact velocity of 6.0 m/s

下载: 全尺寸图片幻灯片

图 11 不同SOC的锂离子电池在质量为50.20 kg的冲头以5.0 m/s的速度冲击下所受到冲击力及其电压随时间的变化

Figure 11. Impact force- and voltage-time curves of lithium-ion batteries with different SOCs impacted by a 50.20-kg punch at 5.0 m/s

下载: 全尺寸图片幻灯片

图 12 在50.20 kg-5.0 m/s冲头的冲击下0.5 SOC锂离子电池结构的变形及其载荷和电压随位移的变化

Figure 12. Structure deformation of the lithium-ion battery with 0.5 SOC impacted by a 50.20-kg and 5.0-m/s punch as well as changes of load and voltage with displacement

下载: 全尺寸图片幻灯片

图 13 在不同质量、不同速度的冲头以恒定能量冲击下锂离子电池所受的冲击力及其电压随时间和位移的变化

Figure 13. Impact force and voltage of lithium-ion batteries subjected to constant impact energy from punches with different masses and different velocities

下载: 全尺寸图片幻灯片

图 14 在质量为139.50 kg的冲头以3.0 m/s的速度冲击下锂离子电池受到冲击力及其电压随时间的变化以及电芯中部和底部的XCT图像

Figure 14. Impact force- and voltage-time curves of the lithium-ion battery impacted by the 139.50-kg punch with the velocity of 3.0 m/s as well as XCT images for the battery cell middle and bottom

下载: 全尺寸图片幻灯片

图 15 在质量为78.45 kg的冲头以4.0 m/s的速度冲击下锂离子电池受到冲击力及其电压随时间的变化以及电芯中部和底部的XCT图像

Figure 15. Impact force- and voltage-time curves of the lithium-ion battery impacted by the 78.45-kg punch with the velocity of 4.0 m/s as well as XCT images for the battery cell middle and bottom

下载: 全尺寸图片幻灯片

图 16 在质量为50.20 kg的冲头以5.0 m/s的速度冲击下锂离子电池受到的冲击力及其电压随时间的变化以及电芯中部和底部的XCT图像

Figure 16. Impact force- and voltage-time curves of the lithium-ion battery impacted by the 50.20-kg punch with the velocity of 5.0 m/s as well as XCT images for the battery cell middle and bottom

下载: 全尺寸图片幻灯片

图 17 在质量为34.87 kg的冲头以6.0 m/s的速度冲击下锂离子电池受到冲击载荷及其电压随时间的变化以及电芯中部和底部的XCT图像

Figure 17. Impact force- and voltage-time curves of the lithium-ion battery impacted by the 34.87-kg punch with the velocity of 6.0 m/s as well as XCT images for the battery cell middle and bottom

下载: 全尺寸图片幻灯片

图 18 在质量为29.71 kg的冲头以6.5 m/s的速度冲击下锂离子电池受到冲击载荷及其电压随时间的变化以及电芯中部和底部的XCT图像

Figure 18. Impact force- and voltage-time curves of the lithium-ion battery impacted by the 29.71-kg punch with the velocity of 6.5 m/s as well as XCT images for the battery cell middle and bottom

下载: 全尺寸图片幻灯片

图 19 在不同冲击质量和不同冲击速度下的冲击载荷曲线及硬短路失效时间

Figure 19. Impact load profiles and hard short-circuit failure times at different impact masses and different impact velocities

下载: 全尺寸图片幻灯片

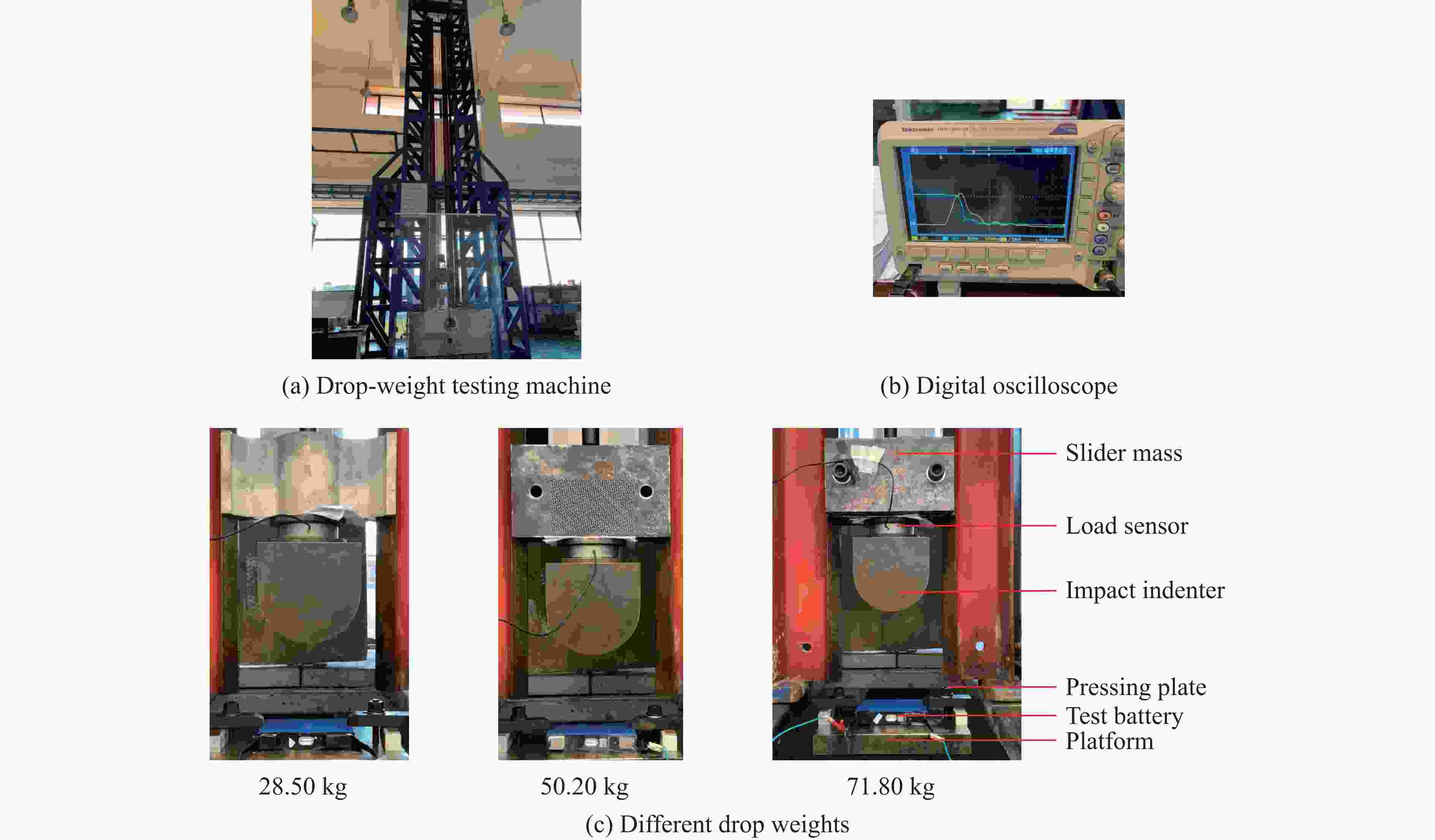
表 1 由冲击速度和落锤质量不同组合确定的冲击能量

Table 1. Impact energies determined by different combinations of impact velocity and hammer mass

冲击速度/(m∙s⁻¹)	下落高度/mm	冲击能量/J
冲击速度/(m∙s⁻¹)	下落高度/mm	28.50 kg	50.20 kg	71.80 kg
1.0	51	14.25	25.10	35.90
2.0	204	57.00	100.40	143.60
3.0	459	128.25	225.90	323.10
4.0	817	228.00	401.60	574.40
5.0	1276	356.25	627.50	897.50
6.0	1838	513.00	903.60	1292.40

下载: 导出CSV

表 2 硬短路失效点的能量

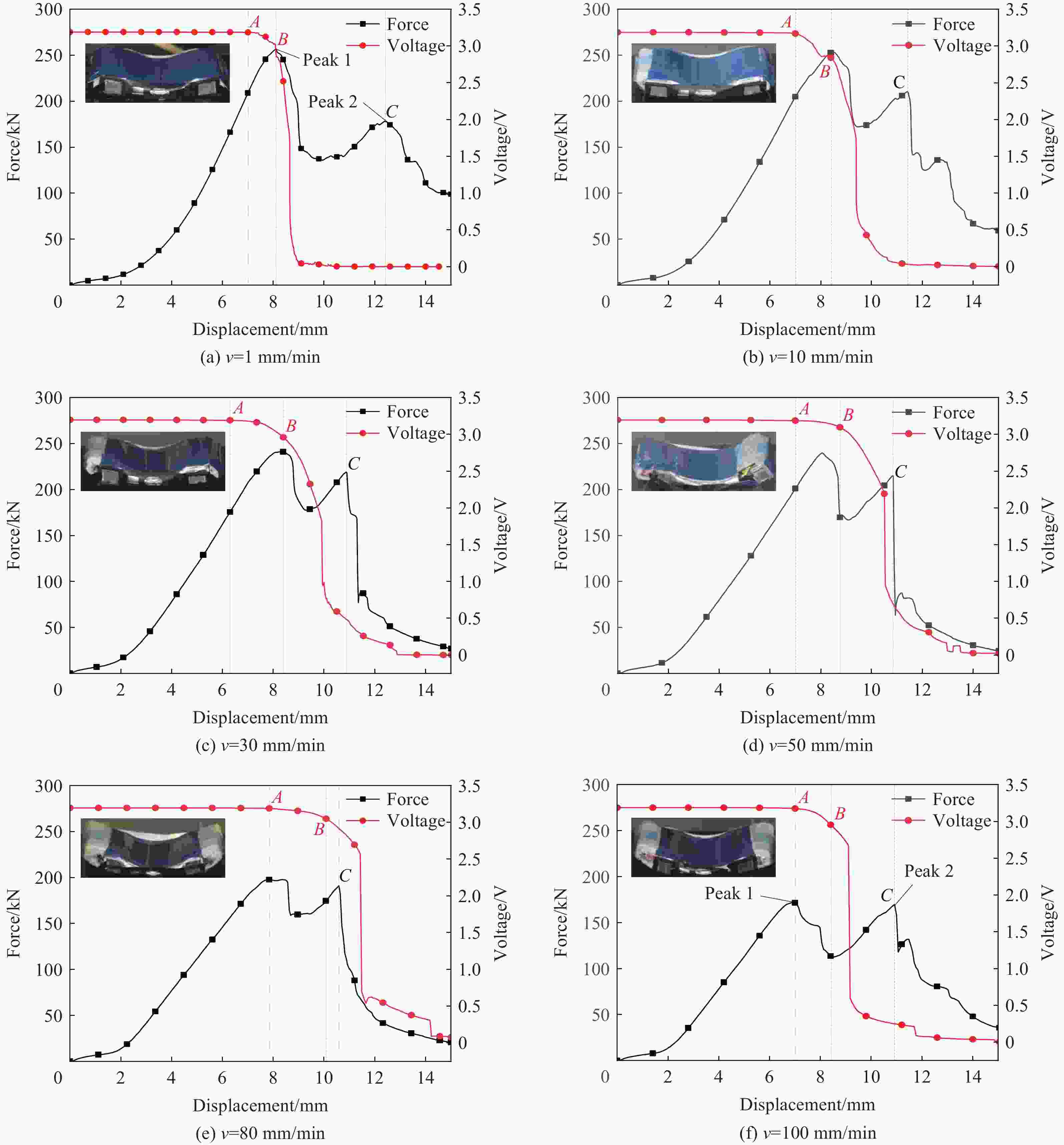
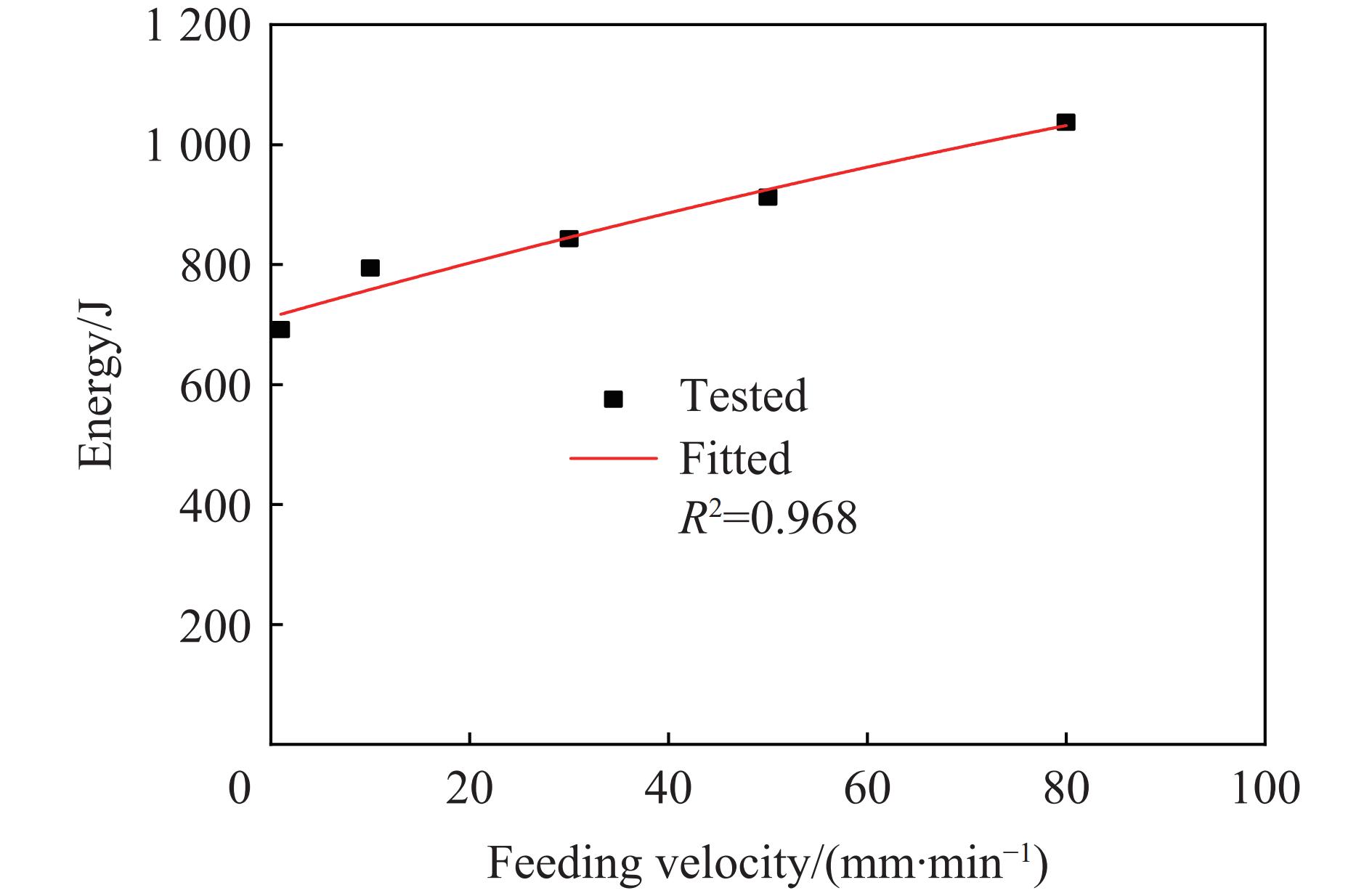
Table 2. Energies at hard short circuit failure points

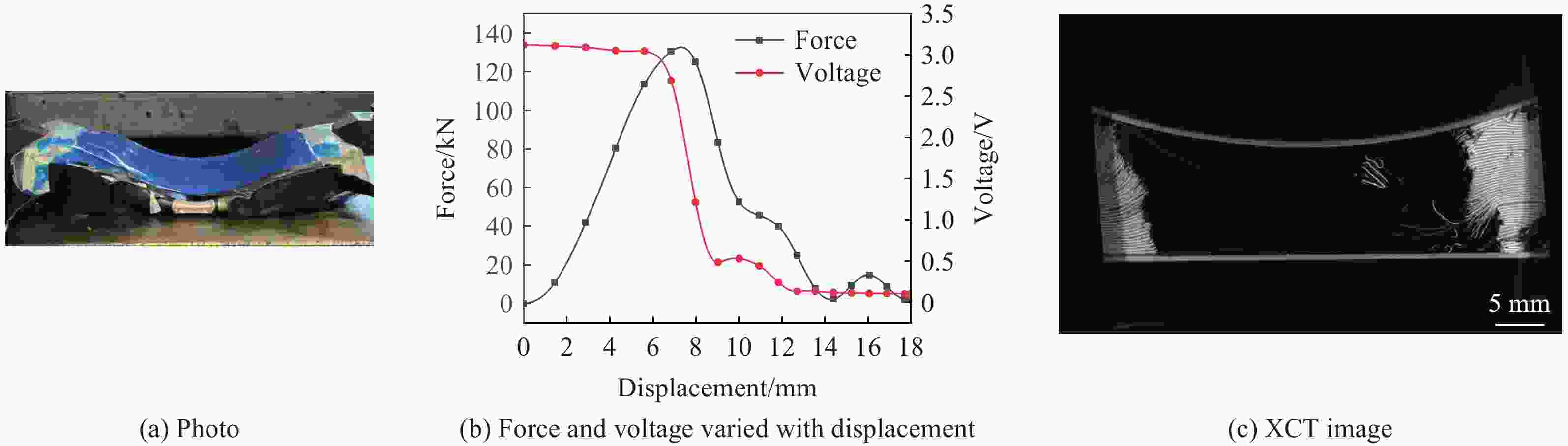
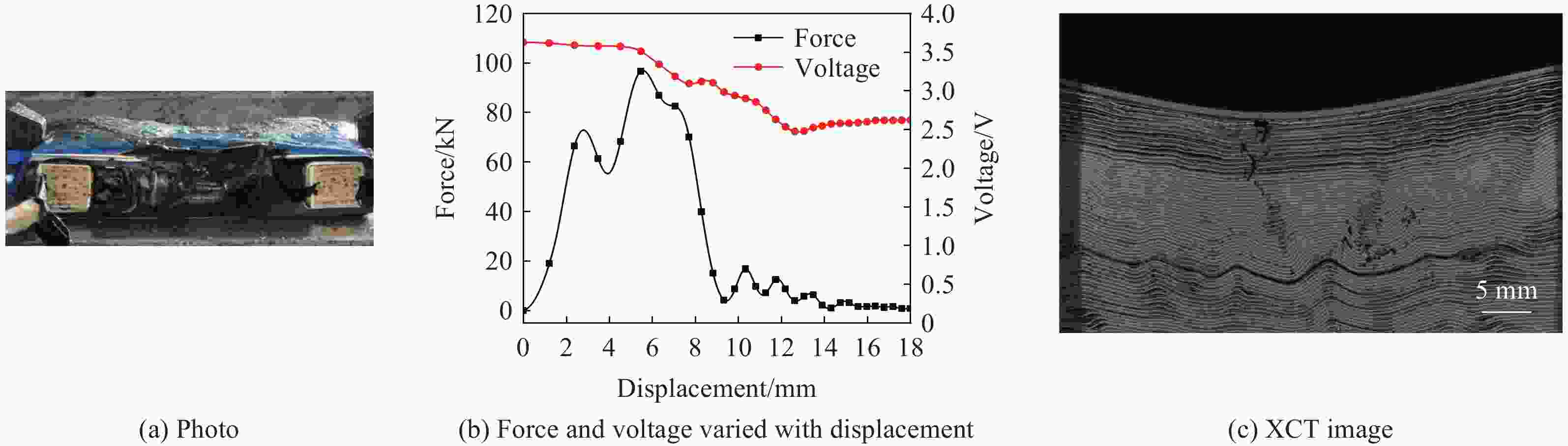
进给速度/(mm∙min⁻¹)	位移/mm	载荷/kN	失效点能量/J
1	8.06	256.24	691.61
10	8.40	252.49	794.16
30	8.40	241.06	842.76
50	8.76	169.57	912.06
80	10.08	174.55	1036.69
100	8.40	113.61	692.85

下载: 导出CSV

表 3 恒定冲击能量下的不同冲击速度、落锤初始高度和冲击质量

Table 3. Different impact velocities, initial drop height and impact masses at constant impact energy

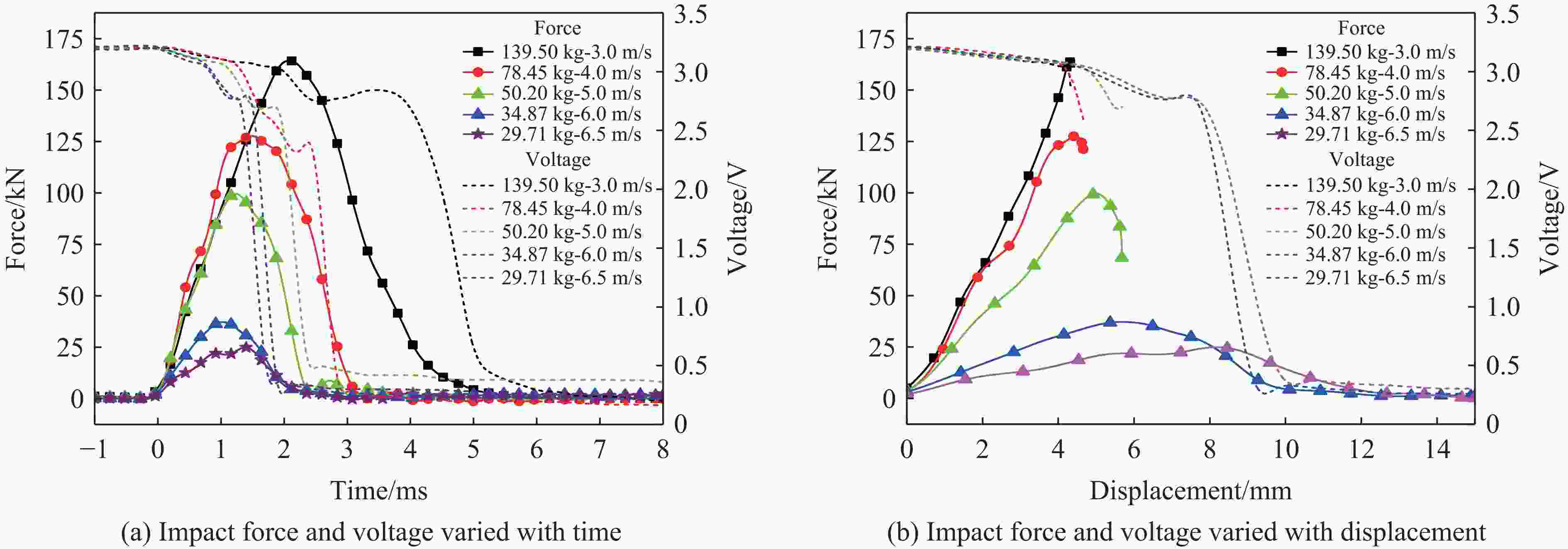
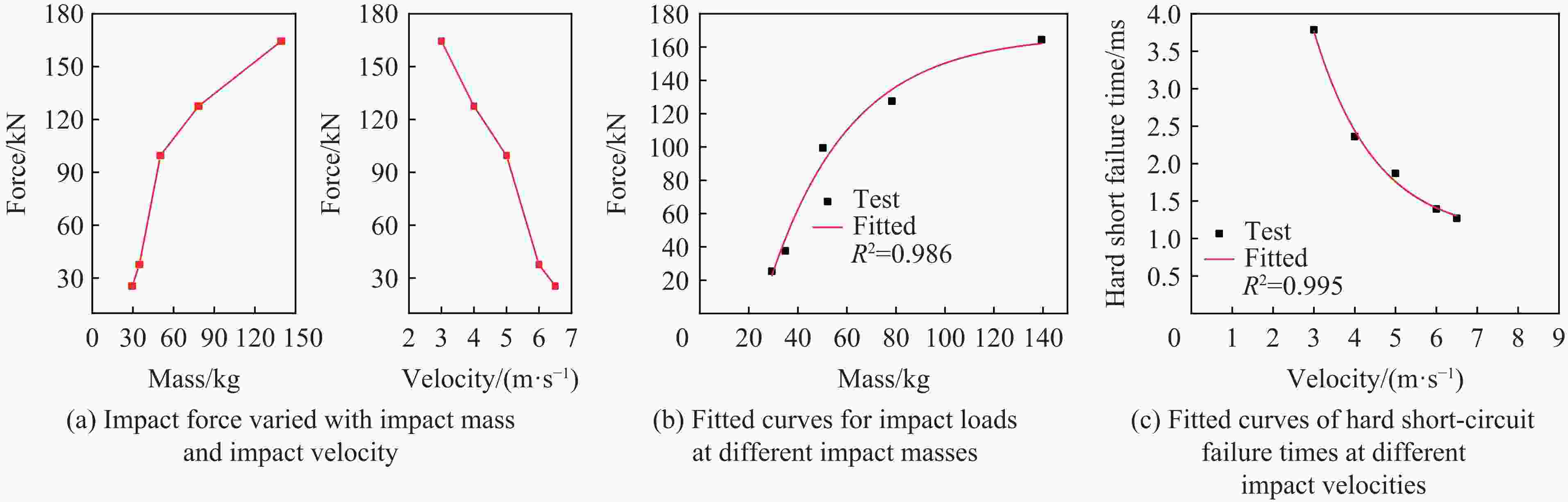
冲击能量/J	冲击速度/(m∙s⁻¹)	落锤初始高度/mm	冲击质量/kg
627.75	3.0	459	139.50
627.60	4.0	817	78.45
627.50	5.0	1276	50.20
627.66	6.0	1838	34.87
627.62	6.5	2179	29.71

下载: 导出CSV

表 4 恒定冲击能量下冲击试验的峰值载荷和硬短路失效时间点

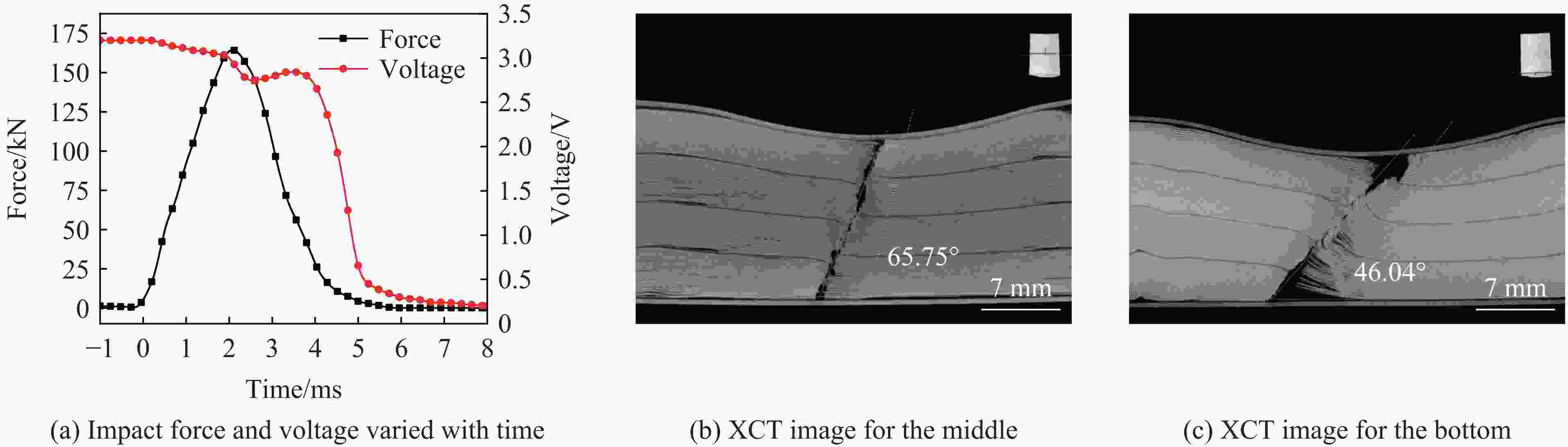
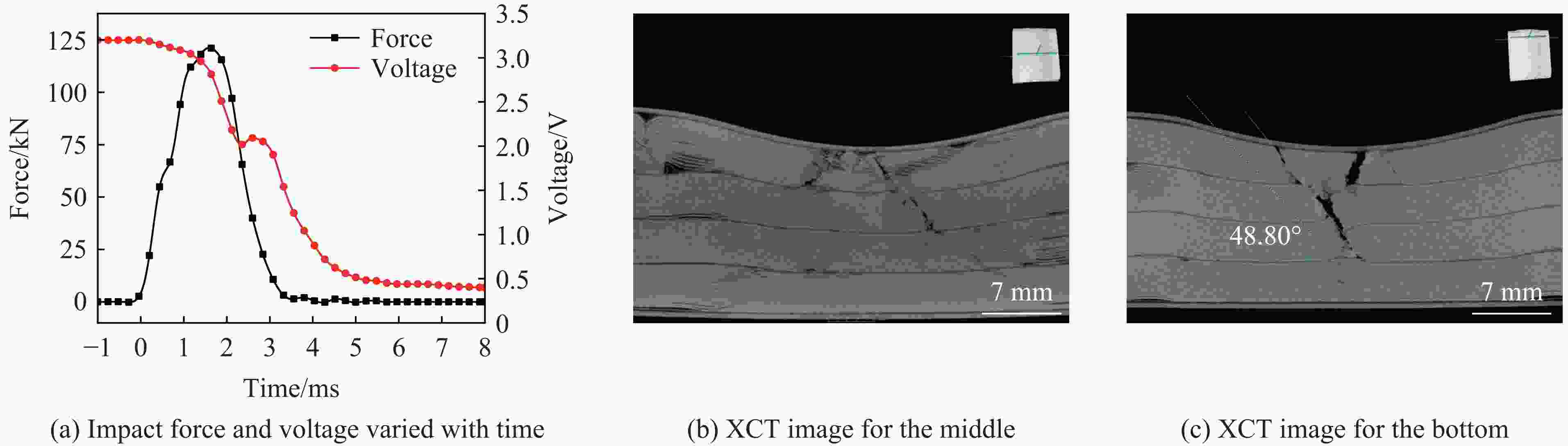
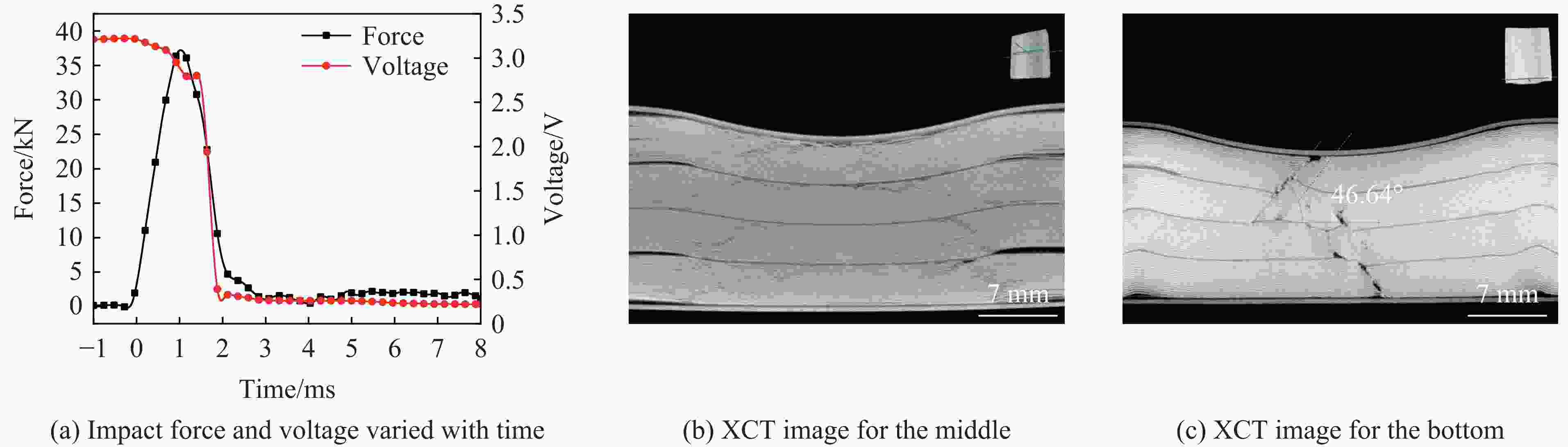
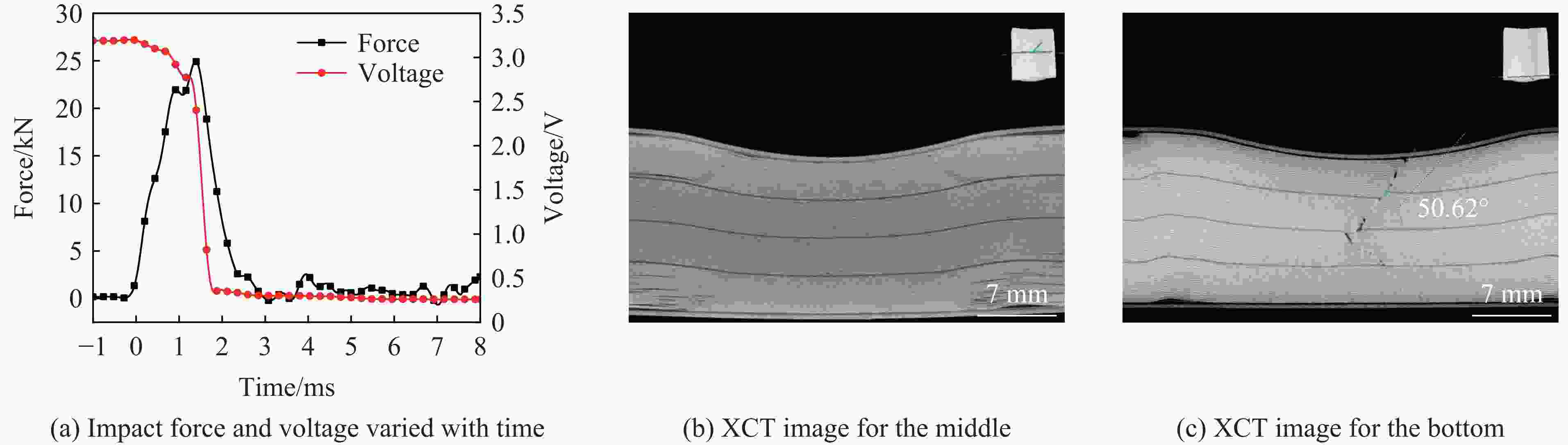
Table 4. Peak loads and hard short-circuit failure time points for impact tests at constant impact energy

冲击速度/(m∙s⁻¹)	冲击质量/kg	峰值载荷/kN	硬短路失效时间/ms
3.0	139.50	164.43	3.79
4.0	78.45	127.60	2.36
5.0	50.20	99.46	1.87
6.0	34.87	37.60	1.39
6.5	29.71	25.40	1.27

下载: 导出CSV

参考文献(27)

[1]	LIU B H, JIA Y K, YUAN C H, et al. Safety issues and mechanisms of lithium-ion battery cell upon mechanical abusive loading: a review [J]. Energy Storage Materials, 2020, 24: 85–112. DOI: 10.1016/j.ensm.2019.06.036.
[2]	XIA Y, WIERZBICKI T, SAHRAEI E, et al. Damage of cells and battery packs due to ground impact [J]. Journal of Power Sources, 2014, 267: 78–97. DOI: 10.1016/j.jpowsour.2014.05.078.
[3]	XU J, LIU B H, WANG X Y, et al. Computational model of 18650 lithium-ion battery with coupled strain rate and SOC dependencies [J]. Applied Energy, 2016, 172: 180–189. DOI: 10.1016/j.apenergy.2016.03.108.
[4]	XU J, LIU B H, WANG L B, et al. Dynamic mechanical integrity of cylindrical lithium-ion battery cell upon crushing [J]. Engineering Failure Analysis, 2015, 53: 97–110. DOI: 10.1016/j.engfailanal.2015.03.025.
[5]	JIA Y K, YIN S, LIU B H, et al. Unlocking the coupling mechanical-electrochemical behavior of lithium-ion battery upon dynamic mechanical loading [J]. Energy, 2019, 166: 951–960. DOI: 10.1016/j.energy.2018.10.142.
[6]	KISTERS T, SAHRAEI E, WIERZBICKI T. Dynamic impact tests on lithium-ion cells [J]. International Journal of Impact Engineering, 2017, 108: 205–216. DOI: 10.1016/j.ijimpeng.2017.04.025.
[7]	KISTERS T, GILAKI M, NAU S, et al. Modeling of dynamic mechanical response of Li-ion cells with homogenized electrolyte-solid interactions [J]. Journal of Energy Storage, 2022, 49: 104069. DOI: 10.1016/j.est.2022.104069.
[8]	RATNER A, BEAUMONT R, MASTERS I. Dynamic mechanical compression impulse of lithium-ion pouch cells [J]. Energies, 2020, 13(8): 2105. DOI: 10.3390/en13082105.
[9]	CHEN X P, WANG T, ZHANG Y, et al. Dynamic behavior and modeling of prismatic lithium-ion battery [J]. International Journal of Energy Research, 2020, 44(4): 2984–2997. DOI: 10.1002/er.5126.
[10]	CHEN X P, WANG T, ZHANG Y, et al. Dynamic mechanical behavior of prismatic lithium-ion battery upon impact [J]. International Journal of Energy Research, 2019, 43: 7421–7432. DOI: 10.1002/er.4774.
[11]	KOTTER P, KISTERS T, SCHLEICHER A. Dynamic impact tests to characterize the crashworthiness of large-format lithium-ion cells [J]. Journal of Energy Storage, 2019, 26: 100948. DOI: 10.1016/j.est.2019.100948.
[12]	HU L L, ZHANG Z W, ZHOU M Z, et al. Crushing behaviors and failure of packed batteries [J]. International Journal of Impact Engineering, 2020, 143: 103618. DOI: 10.1016/j.ijimpeng.2020.103618.
[13]	SAHRAEI E, KAHN M, MEIER J, et al. Modelling of cracks developed in lithium-ion cells under mechanical loading [J]. RSC Advances, 2015, 5(98): 80369–80380. DOI: 10.1039/c5ra17865g.
[14]	WANG H, SIMUNOVIC S, MALEKI H, et al. Internal configuration of prismatic lithium-ion cells at the onset of mechanically induced short circuit [J]. Journal of Power Sources, 2016, 306: 424–430. DOI: 10.1016/j.jpowsour.2015.12.026.
[15]	CHUNG S H, TANCOGNE-DEJEAN T, ZHU J E, et al. Failure in lithium-ion batteries under transverse indentation loading [J]. Journal of Power Sources, 2018, 389: 148–159. DOI: 10.1016/j.jpowsour.2018.04.003.
[16]	ZHU X Q, WANG H, WANG X, et al. Internal short circuit and failure mechanisms of lithium-ion pouch cells under mechanical indentation abuse conditions: an experimental study [J]. Journal of Power Sources, 2020, 455: 227939. DOI: 10.1016/j.jpowsour.2020.227939.
[17]	ZHU F, ZHOU R Z, SYPECK D, et al. Failure behavior of prismatic Li-ion battery cells under abuse loading condition: a combined experimental and computational study [J]. Journal of Energy Storage, 2022, 48: 103969. DOI: 10.1016/j.est.2022.103969.
[18]	LI W, XING B B, WATKINS T R, et al. Damage of prismatic lithium-ion cells subject to bending: test, model, and detection [J]. EcoMat, 2022, 4(6): e12257. DOI: 10.1002/eom2.12257.
[19]	XING B B, XIAO F Y, KOROGI Y, et al. Direction-dependent mechanical-electrical-thermal responses of large-format prismatic Li-ion battery under mechanical abuse [J]. Journal of Energy Storage, 2021, 43: 103270. DOI: 10.1016/j.est.2021.103270.
[20]	WANG L B, CHEN J Y, LI J P, et al. A novel anisotropic model for multi-stage failure threshold of lithium-ion battery subjected to impact loading [J]. International Journal of Mechanical Sciences, 2022, 236: 107757. DOI: 10.1016/j.ijmecsci.2022.107757.
[21]	KISTERS T, KUDER J, TÖPEL A, et al. Strain-rate dependence of the failure behavior of lithium-ion pouch cells under impact loading [J]. Journal of Energy Storage, 2021, 41: 102901. DOI: 10.1016/j.est.2021.102901.
[22]	LIU Y J, XIA Y, XING B B, et al. Mechanical-electrical-thermal responses of lithium-ion pouch cells under dynamic loading: a comparative study between fresh cells and aged ones [J]. International Journal of Impact Engineering, 2022, 166: 104237. DOI: 10.1016/j.ijimpeng.2022.104237.
[23]	LI W, ZHU J E, XIA Y, et al. Data-driven safety envelope of lithium-ion batteries for electric vehicles [J]. Joule, 2019, 3(11): 2703–2715. DOI: 10.1016/j.joule.2019.07.026.
[24]	CHEN X P, YUAN Q, WANG T, et al. Experimental study on the dynamic behavior of prismatic lithium-ion battery upon repeated impact [J]. Engineering Failure Analysis, 2020, 115: 104667. DOI: 10.1016/j.engfailanal.2020.104667.
[25]	ZHANG H J, ZHOU M Z, HU L L, et al. Mechanism of the dynamic behaviors and failure analysis of lithium-ion batteries under crushing based on stress wave theory [J]. Engineering Failure Analysis, 2020, 108: 104290. DOI: 10.1016/j.engfailanal.2019.104290.
[26]	KALNAUS S, WANG H, WATKINS T R, et al. Features of mechanical behavior of EV battery modules under high deformation rate [J]. Extreme Mechanics Letters, 2019, 32: 100550. DOI: 10.1016/j.eml.2019.100550.
[27]	李志杰. 新能源汽车方形锂离子电池内部芯层载荷变形失效试验与仿真分析 [D]. 广州: 华南理工大学, 2021. DOI: 10.27151/d.cnki.ghnlu.2021.001195. LI Z J. Load deformation failure test and simulation analysis for internal configuration of prismatic lithium-ion batteries on new energy vehicle [D]. Guangzhou: South China University of Technology, 2021. DOI: 10.27151/d.cnki.ghnlu.2021.001195.