Numerical investigation on dynamic tensile fracture in concrete material by non-ordinary state-based peridynamics
-
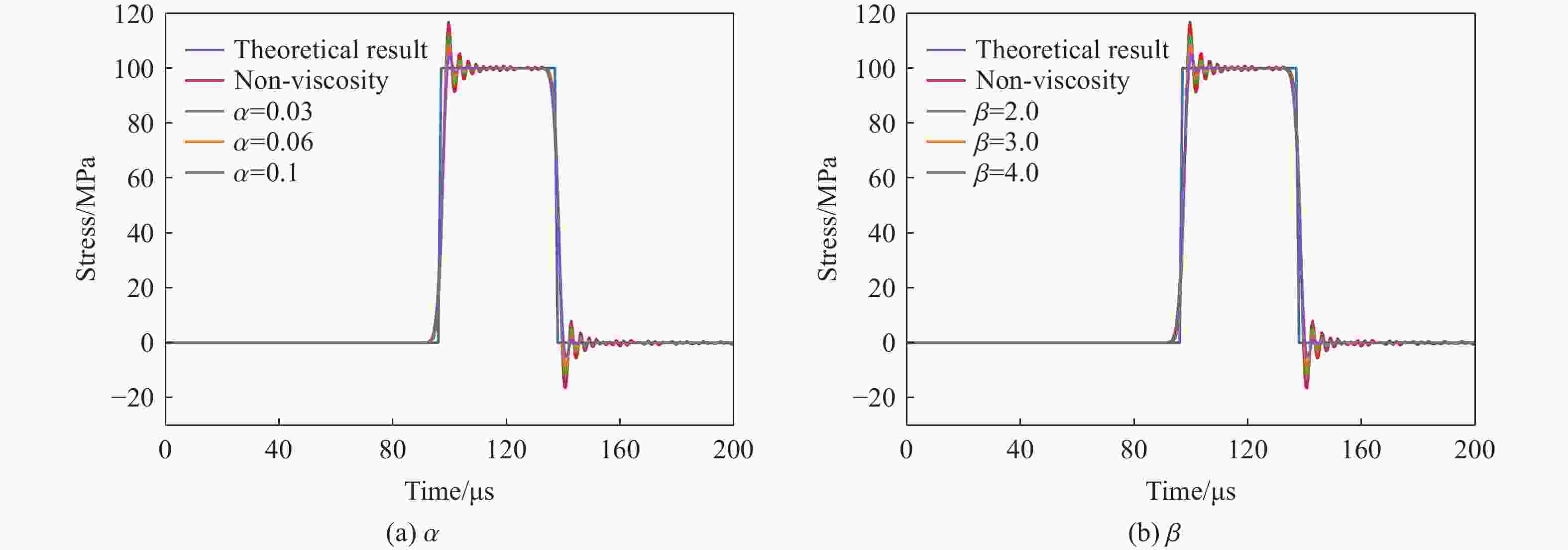
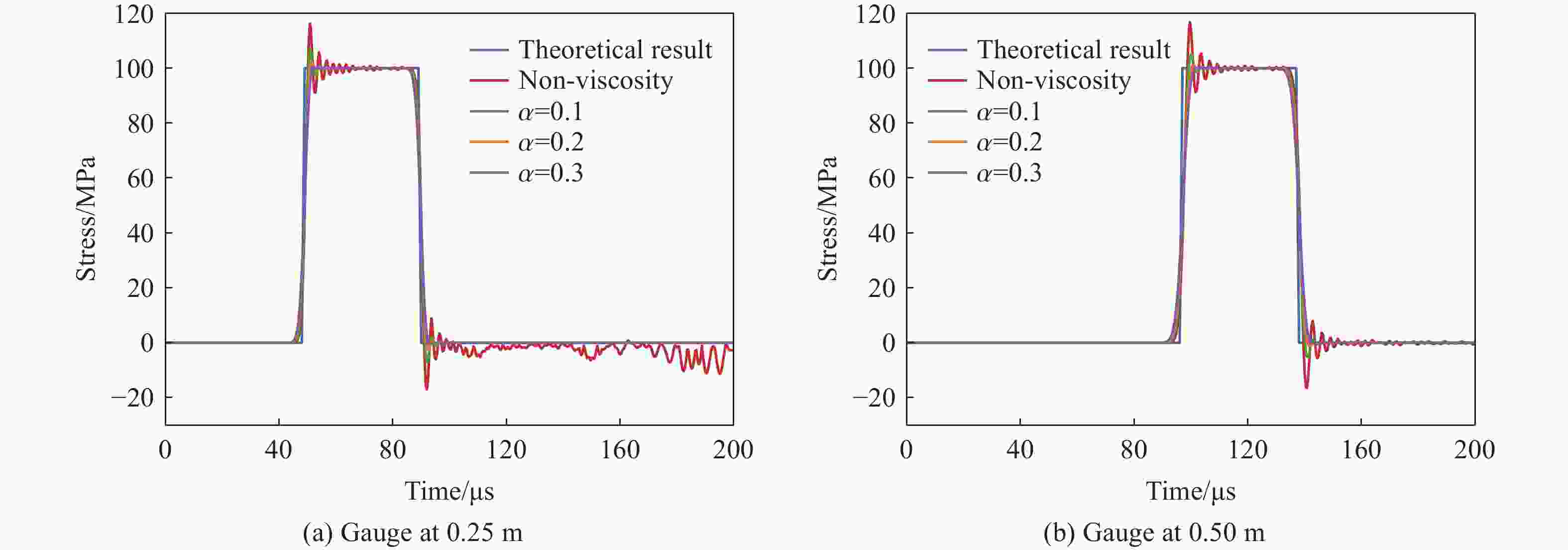
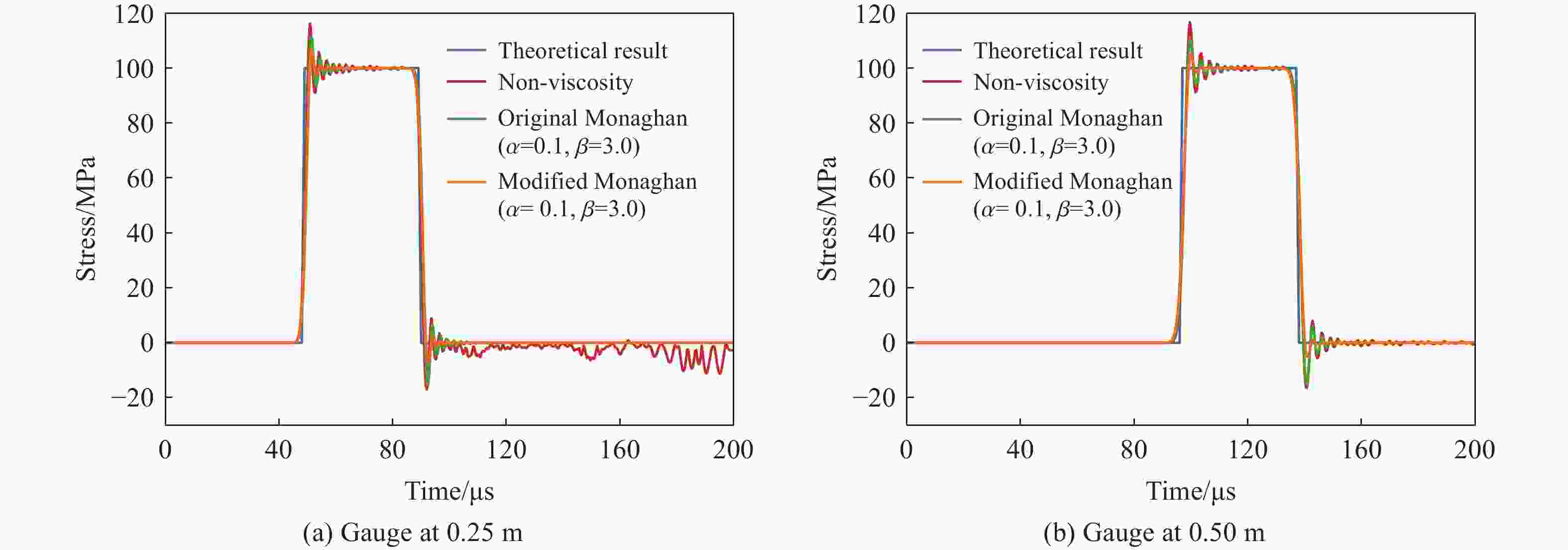
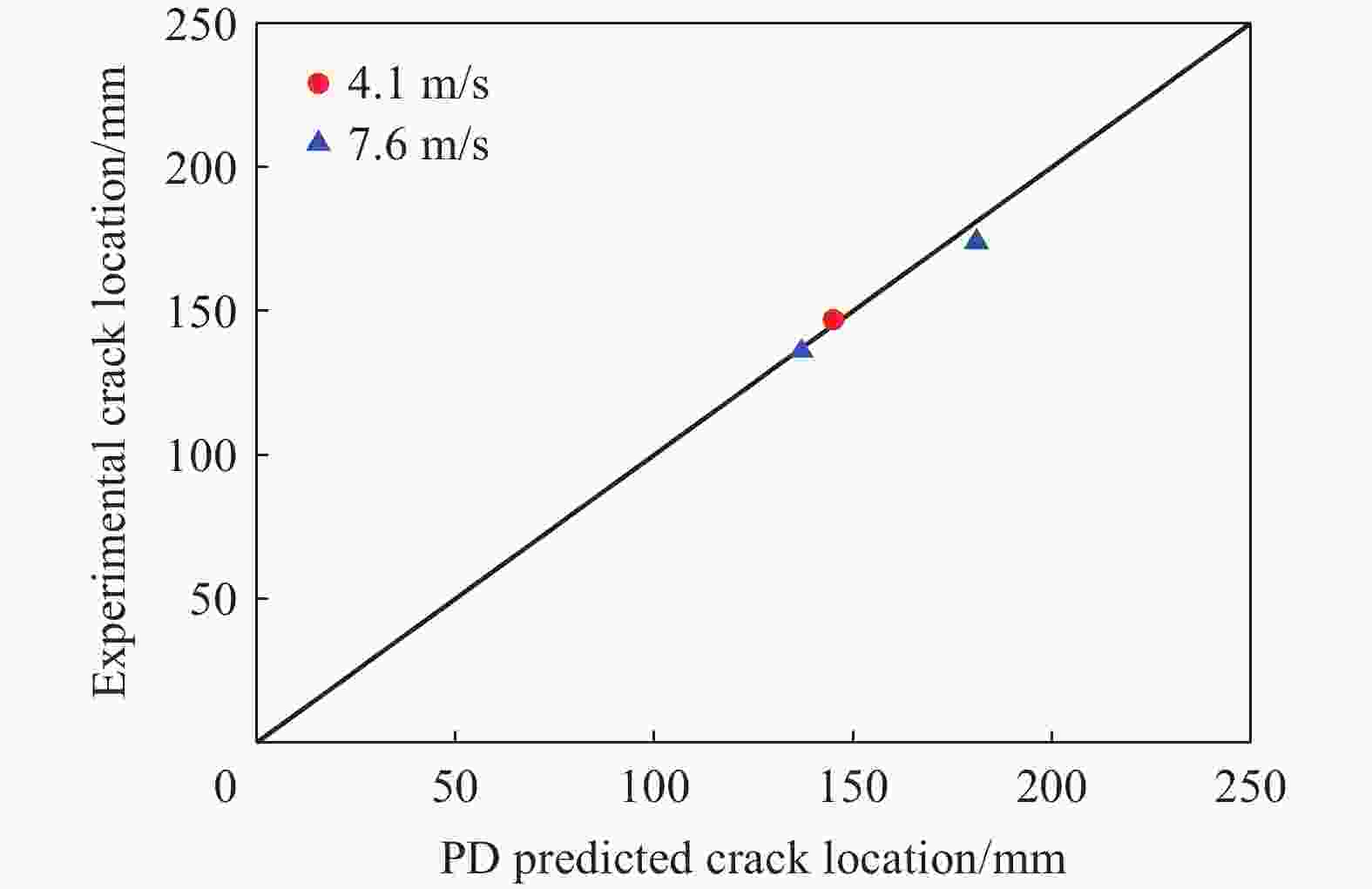
摘要: 为了准确预测冲击爆炸荷载作用下混凝土材料的动态拉伸断裂破坏，基于非常规态近场动力学理论框架，本文首先建立了修正的Monaghan人工体积黏性计算方法用于消除数值振荡，然后将前期建立的等效计算应变率方法植入到课题组前期研发的Kong-Fang混凝土材料模型中，用以准确计算应变率突变时的应变率效应。在此基础上，开展了一维杆中的弹性波传播的数值模拟，发现在力矢量状态上额外附加修正的Monaghan人工体积黏性力矢量状态，可有效地抑制由变形梯度近似导致的非物理数值振荡现象，进而讨论分析了人工体积黏性参数的影响并给出参数建议值。最后将模型用于混凝土试件层裂的数值模拟，对比分析了人工体积黏性、不同应变率效应计算方法对动态拉伸断裂预测结果的影响规律，数值模拟结果表明，准确预测混凝土材料动态拉伸断裂破坏需同时考虑修正的Monaghan人工体积黏性和等效计算应变率，建立的考虑修正的Monaghan人工体积黏性和等效计算应变率的非常规态近场动力学模型可以较好地预测裂缝位置和数量，为冲击爆炸荷载作用下混凝土材料动态拉伸断裂破坏的数值模拟提供了新思路。
-
关键词:
- 动态断裂 /
- 修正的Monaghan人工体积黏性 /
- 等效计算应变率 /
- 非常规态近场动力学
Abstract: To accurately predict the dynamic tensile fracture in concrete materials subjected to impact and blast loadings, this study first establishes a modified Monaghan artificial bulk viscosity computation method within the framework of a non-ordinary state-based peridynamics (NOSB-PD) theory to eliminate numerical oscillations. Subsequently, the corrected strain-rate computation method, previously developed, is integrated into the Kong-Fang concrete material model, which was proposed earlier by the research group to calculate accurately the strain-rate effect during sudden changes. Based on the two methods above, numerical simulations of elastic wave propagation in a one-dimensional rod are conducted, and the results demonstrate that the additional inclusion of the modified Monaghan artificial bulk viscosity force vector state into the original force vector state can effectively suppress the non-physical numerical oscillations caused by the deformation gradient approximation. The superiority of the modified Monaghan artificial bulk viscosity is validated through comparative analysis with the original Monaghan artificial bulk viscosity. Furthermore, the influence of the modified Monaghan artificial bulk viscosity parameters is investigated, and recommended values for these parameters are provided. Finally, the aforementioned model is used to numerically simulate the spall test in concrete specimens, where the effects of including or excluding the modified Monaghan artificial bulk viscosity and different strain-rate computation methods on the prediction results of dynamic tensile fracture are compared and analyzed. The numerical simulation results demonstrate that accurately predicting the dynamic tensile fracture in concrete materials requires simultaneous consideration of the modified Monaghan artificial bulk viscosity and corrected strain-rate computation. The established non-ordinary state-based peridynamics model that accounts for both the modified Monaghan artificial bulk viscosity and corrected strain-rate computation demonstrates strong capabilities in predicting crack locations and quantities based on both qualitative and quantitative analysis metrics. This work provides new insights into the numerical simulation of dynamic tensile fracture in concrete materials under impact and blast loadings. -
图 2 一维杆中的弹性波传播数值模型示意图
Figure 2. Numerical model for wave propagation in one-dimensional rod
图 3 不考虑人工体积黏性时一维杆中0.25 m处测点的应力时程曲线
Figure 3. Stress-time history of gauge located at 0.25 m without consideration of artificial bulk viscosity
图 4 考虑人工体积黏性时一维杆中0.25 m处测点的应力时程曲线
Figure 4. Stress-time history of gauge located at 0.25 m with consideration of artificial bulk viscosity
图 5 不同黏性参数下0.25 m处测点的应力时程曲线
Figure 5. Stress-time history of gauge located at 0.25 m with different viscosity parameters
图 6 不同黏性参数下0.50 m处测点的应力时程曲线
Figure 6. Stress-time history of gauge located at 0.50 m with different viscosity parameters
图 7 不同黏性参数下不同测点的应力时程曲线
Figure 7. Stress-time history of different gauges with different viscosity parameters
图 8 不同黏性方式下不同测点的应力时程曲线
Figure 8. Stress-time history of different gauges with different viscosity modes
图 10 子弹冲击速度4.1 m/s工况下的δ收敛性
Figure 10. Convergence of δ under the condition of projectile impact velocity with 4.1 m/s
图 11 子弹冲击速度4.1 m/s工况下的m收敛性
Figure 11. Convergence of m under the condition of projectile impact velocity with 4.1 m/s
图 12 不同子弹冲击速度下不同计算方法预测的混凝土试件断裂破坏及与试验的对比
Figure 12. Experimental and numerical fracture and failure in concrete specimens with different projectile impact velocity
图 13 不同冲击速度下试验与PD模拟的裂缝位置对比
Figure 13. Comparisons of crack locations between test and PD simulations under different impact velocities
表 1 层裂试验PD模拟参数
Table 1. Parameters required in PD simulations for spall tests
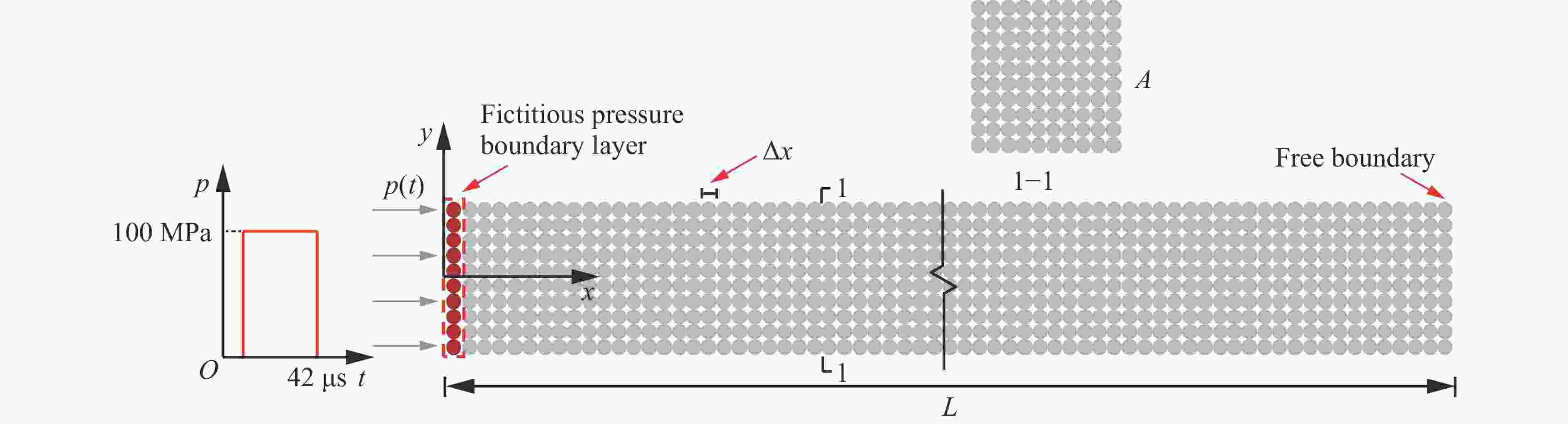
参数 取值 参数 取值 粒子间距Δx 4 × 10−3 m 密度ρ 2 400 kg/m3 邻域半径δ 3Δx 强度面参数a1 0.5876 时间步Δt 4 × 10−7 s 强度面参数a2 0.025/fc Newmark常数γ 0.6 损伤参数d1 0.04 Newmark常数ψ 0.6 损伤参数d2 1.5 抗压强度fc 35 MPa 流动法则参数ω 0.5 抗拉强度ft 3.22 MPa 断裂应变εfrac 0.01 弹性模量E 28 GPa 时间迟滞因子η 1 × 10−4 s 泊松比v 0.3 状态方程 文献[4] 
下载: 导出CSV
-
[1] 方秦, 陈小伟. 冲击爆炸效应与工程防护专辑·编者按 [J]. 中国科学: 物理学力学天文学, 2020, 50(2): 024601. DOI: 10.1360/SSPMA-2019-0404.FANG Q, CHEN X W. Special issue on impact and explosion effect and engineering protection [J]. Scientia Sinica Physica, Mechanica & Astronomica, 2020, 50(2): 024601. DOI: 10.1360/SSPMA-2019-0404. [2] KONG X Z, FANG Q, WU H, et al. Numerical predictions of cratering and scabbing in concrete slabs subjected to projectile impact using a modified version of HJC material model [J]. International Journal of Impact Engineering, 2016, 95: 61–71. DOI: 10.1016/j.ijimpeng.2016.04.014. [3] KONG X Z, FANG Q, LI Q M, et al. Modified K&C model for cratering and scabbing of concrete slabs under projectile impact [J]. International Journal of Impact Engineering, 2017, 108: 217–228. DOI: 10.1016/j.ijimpeng.2017.02.016. [4] KONG X Z, FANG Q, CHEN L, et al. A new material model for concrete subjected to intense dynamic loadings [J]. International Journal of Impact Engineering, 2018, 120: 60–78. DOI: 10.1016/j.ijimpeng.2018.05.006. [5] KONG X Z, FANG Q, ZHANG J H, et al. Numerical prediction of dynamic tensile failure in concrete by a corrected strain-rate dependent nonlocal material model [J]. International Journal of Impact Engineering, 2020, 137: 103445. DOI: 10.1016/j. ijimpeng.2019.103445. DOI: 10.1016/j.ijimpeng.2019.103445. [6] KHOE Y S, WEERHEIJM J. Limitations of smeared crack models for dynamic analysis of concrete [C]//The 12th International LS-DYNA Users Conference. Constitutive Models, 2012. [7] KONG X Z, FANG Q, HONG J. A new damage-based nonlocal model for dynamic tensile failure of concrete material [J]. International Journal of Impact Engineering, 2019, 132: 103336. DOI: 10.1016/j.ijimpeng.2019.103336. [8] XU K, LU Y. Numerical simulation study of spallation in reinforced concrete plates subjected to blast loading [J]. Computers & Structures, 2006, 84(5/6): 431–438. DOI: 10.1016/j.compstruc.2005.09.029. [9] LI J, HAO H. Numerical study of concrete spall damage to blast loads [J]. International Journal of Impact Engineering, 2014, 68: 41–55. DOI: 10.1016/j.ijimpeng.2014.02.001. [10] 孔祥振, 方秦. 基于SPH方法对强动载下混凝土结构损伤破坏的数值模拟研究 [J]. 中国科学: 物理学 力学 天文学, 2020, 50(2): 25–33. DOI: 10.1360/SSPMA-2019-0186.KONG X Z, FANG Q. Numerical predictions of failures in concrete structures subjected to intense dynamic loadings using the smooth particle hydrodynamics method [J]. Scientia Sinica Physica, Mechanica & Astronomica, 2020, 50(2): 25–33. DOI: 10.1360/SSPMA-2019-0186. [11] YANG Y Z, FANG Q, KONG X Z. Failure mode and stress wave propagation in concrete target subjected to a projectile penetration followed by charge explosion: experimental and numerical investigation [J]. International Journal of Impact Engineering, 2023, 177: 104595. DOI: 10.1016/j.ijimpeng.2023.104595. [12] SILLING S A. Reformulation of elasticity theory for discontinuities and long-range forces [J]. Journal of the Mechanics and Physics of Solids, 2000, 48(1): 175–209. DOI: 10.1016/S0022-5096(99)00029-0. [13] SILLING S A, EPTON M, WECKNER O, et al. Peridynamic states and constitutive modeling [J]. Journal of Elasticity, 2007, 88(2): 151–184. DOI: 10.1007/s10659-007-9125-1. [14] LIU X, KONG X Z, FANG Q, et al. Peridynamics modelling of projectile penetration into concrete targets [J]. International Journal of Impact Engineering, 2025, 195: 105110. DOI: 10.1016/j.ijimpeng.2024.105110. [15] LITTLEWOOD D J. Simulation of dynamic fracture using peridynamics, finite element modeling, and contact [C]//ASME International Mechanical Engineering Congress and Exposition. American Society of Mechanical Engineers, 2010, 44465: 209–217. [16] BREITENFELD M S, GEUBELLE P H, WECKNER O, et al. Non-ordinary state-based peridynamic analysis of stationary crack problems [J]. Computer Methods in Applied Mechanics and Engineering, 2014, 272: 233–250. DOI: 10.1016/j.cma.2014.01.002. [17] GU X, ZHANG Q, YU Y T. An effective way to control numerical instability of a nonordinary state-based peridynamic elastic model [J]. Mathematical Problems in Engineering Theory Methods and Applications, 2017(1): 1750876. DOI: 10.1155/2017/1750876. [18] YAGHOOBI A, CHORZEPA M G. Higher-order approximation to suppress the zero-energy mode in non-ordinary state-based peridynamics [J]. Computers & Structures, 2017, 188: 63–79. DOI: 10.1016/j.compstruc.2017.03.019. [19] CHEN H L. Bond-associated deformation gradients for peridynamic correspondence model [J]. Mechanics Research Communications, 2018, 90: 34–41. DOI: 10.1016/j.mechrescom.2018.04.004. [20] GU X, ZHANG Q, MADENCI E, et al. Possible causes of numerical oscillations in non-ordinary state-based peridynamics and a bond-associated higher-order stabilized model [J]. Computer Methods in Applied Mechanics and Engineering, 2019, 357: 112592. DOI: 10.1016/j.cma.2019.112592. [21] ROSSI P. A physical phenomenon which can explain the mechanical behaviour of concrete under high strain rates [J]. Materials and Structures, 1991, 24: 422–424. DOI: 10.1007/BF02472015. [22] REINHARDT H W, WEERHEIJM J. Tensile fracture of concrete at high loading rates taking account of inertia and crack velocity effects [J]. International Journal of Fracture, 1991, 51(1): 31–42. DOI: 10.1007/BF00020851. [23] CURBACH M, EIBL J. Crack velocity in concrete [J]. Engineering Fracture Mechanics, 1990, 35(1/3): 321–326. DOI: 10.1016/0013-7944(90)90210-8. [24] LI Q M, MENG H. About the dynamic strength enhancement of concrete-like materials in a split Hopkinson pressure bar test [J]. International Journal of Solids and Structures, 2003, 40(2): 343–360. DOI: 10.1016/S0020-7683(02)00526-7. [25] ZHANG M, WU H J, LI Q M, et al. Further investigation on the dynamic compressive strength enhancement of concrete-like materials based on split Hopkinson pressure bar tests: part I: experiments [J]. International Journal of Impact Engineering, 2009, 36(12): 1327–1334. DOI: 10.1016/j.ijimpeng.2009.04.009. [26] LI Q M, LU Y B, MENG H. Further investigation on the dynamic compressive strength enhancement of concrete-like materials based on split Hopkinson pressure bar tests: part II: numerical simulations [J]. International Journal of Impact Engineering, 2009, 36(12): 1335–1345. DOI: 10.1016/j.ijimpeng.2009.04.010. [27] LU Y B. , LI Q M. About the dynamic uniaxial tensile strength of concrete-like materials [J]. International Journal of Impact Engineering, 2011, 38(4): 171–180. DOI: 10.1016/j.ijimpeng.2010.10.028. [28] SCHMINDT M J. High pressure and high strain rate behavior of cementitious materials: experiments and elastic/viscoplastic modeling [M]. University of Florida, 2003. [29] TANDON S, FABER K T, BAZANT Z P, et al.Cohesive crack modeling of influence of sudden changes in loading rate on concrete fracture [J]. Engineering Fracture Mechanics, 1995, 52(6): 987–997. DOI: 10.1016/0013-7944(95)00080-F. [30] HOLMQUIST T J, JOHNSON G R. A computational constitutive model for concrete subjected to larger strains, high strain rates and high pressure [C]//The 14th International Symposium Ballistics. USA: American Defense Preparedness Association, 1995, 591–600. [31] MALVAR L J, CRAWFORD J E, WESEVICH J W, et al. A plasticity concrete material model for DYNA3D [J]. International Journal of Impact Engineering, 1997, 19: 847–873. DOI: 10.1016/S0734-743X(97)00023-7. [32] RIEDEL W, THOMA K, HIERMAIER S, et al. Penetration of reinforced concrete by BETA-B-500 numerical analysis using a new macroscopic concrete model for hydrocodes [C]//Proceedings of the 9th International Symposium on the Effects of Munitions with Structures. Berlin-Strausberg Germany, 1999; 315. [33] MONAGHAN J J, GINGOID R A. Shock simulation by the particle method SPH [J]. Journal of Computational Physics, 1983, 52(2): 374–389. DOI: 10.1016/0021-9991(83)90036-0. [34] HUANG X P, KONG X Z, CHEN Z Y, et al. A computational constitutive model for rock in hydrocode [J]. International Journal of Impact Engineering, 2020, 145: 103687. DOI: 10.1016/j.ijimpeng.2020.103687. [35] YANG S B, KONG X Z, WU H, et al. Constitutive modelling of UHPCC material under impact and blast loadings [J]. International Journal of Impact Engineering, 2021, 153: 103860. DOI: 10.1016/j.ijimpeng.2021.103860. [36] XU S, WU P, LI Q, et al. Experimental investigation and numerical simulation on the blast resistance of reactive powder concrete subjected to blast by embedded explosive [J]. Cement and Concrete Composites, 2021, 119: 103989. DOI: 10.1016/j.cemconcomp.2021.103989. [37] YUAN P C, XU S C, LIU J, et al. Experimental and numerical study of blast resistance of geopolymer based high performance concrete sandwich walls incorporated with metallic tube core [J]. Engineering Structures, 2023, 278: 115505. DOI: 10.1016/j.engstruct.2022.115505. [38] HA Y D, BOBARU F. Studies of dynamic crack propagation and crack branching with peridynamics [J]. International Journal of Fracture, 2010, 162(1/2): 229–244. DOI: 10.1007/s10704-010-9442-4. [39] SCHULER H, MAYRHOFER C, THOMA K. Spall experiments for the measurement of the tensile strength and fracture energy of concrete at high strain rates [J]. International Journal of Impact Engineering, 2006, 32(10): 1635–1650. DOI: 10.1016/j.ijimpeng.2005.01.010. -
计量
- 文章访问数: 176
- HTML全文浏览量: 17
- PDF下载量: 69
- 被引次数: 0