固支圆板在多次远场空爆载荷下位移响应的理论模型

郑晓波; 赵宏涛; 李腾; 姚伟光; 宋海生; 桂毓林; 王治

doi:10.11883/bzycj-2024-0488

固支圆板在多次远场空爆载荷下位移响应的理论模型

doi: 10.11883/bzycj-2024-0488

1.
中国工程物理研究院流体物理研究所，四川绵阳 621999
2.
哈尔滨工程大学船舶工程学院，黑龙江哈尔滨 150001

详细信息

作者简介:
郑晓波（1986－　），男，博士，高级工程师，zxb3710@163.com

通讯作者:
桂毓林（1973－　），男，博士，正高级工程师，guiyulin@21cn.com

中图分类号: O347.3; U674.7
计量
- 文章访问数: 285
- HTML全文浏览量: 52
- PDF下载量: 65
- 被引次数: 0
出版历程
- 收稿日期: 2024-12-17
- 修回日期: 2025-03-22
- 网络出版日期: 2025-03-26
- 刊出日期: 2026-02-09

A theoretical model of displacement response of clamped circular plate under multiple far-field blast loads

1.
Institute of Fluid Physics, China Academy of Engineering Physics, Mianyang 621999, Sichuan, China
2.
College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, Heilongjiang, China

摘要

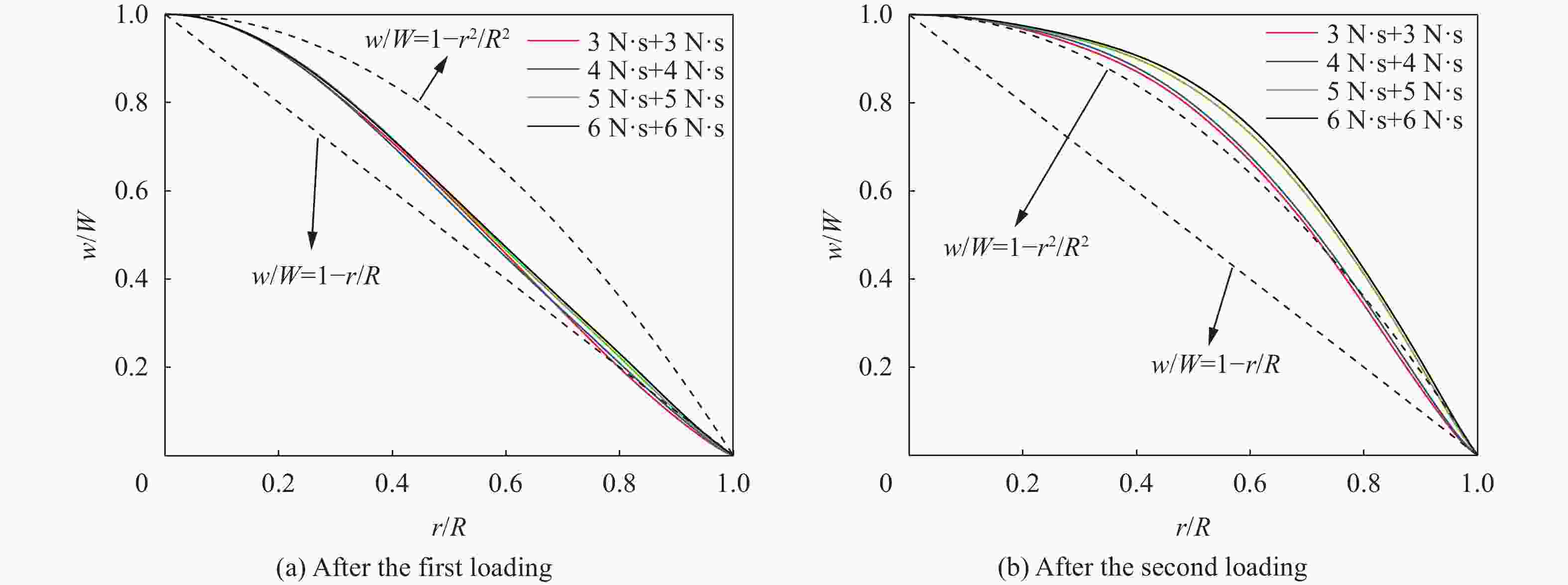
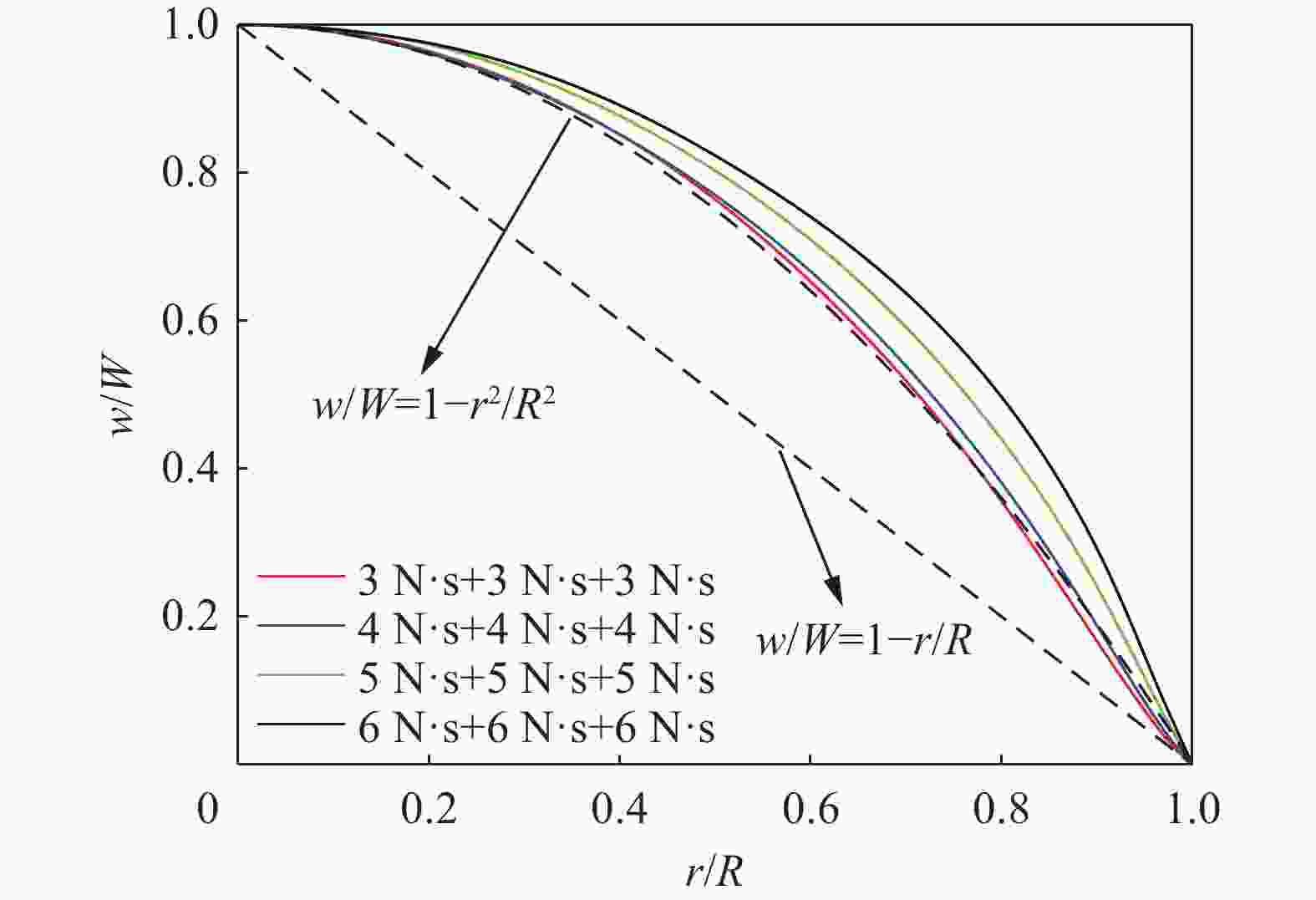
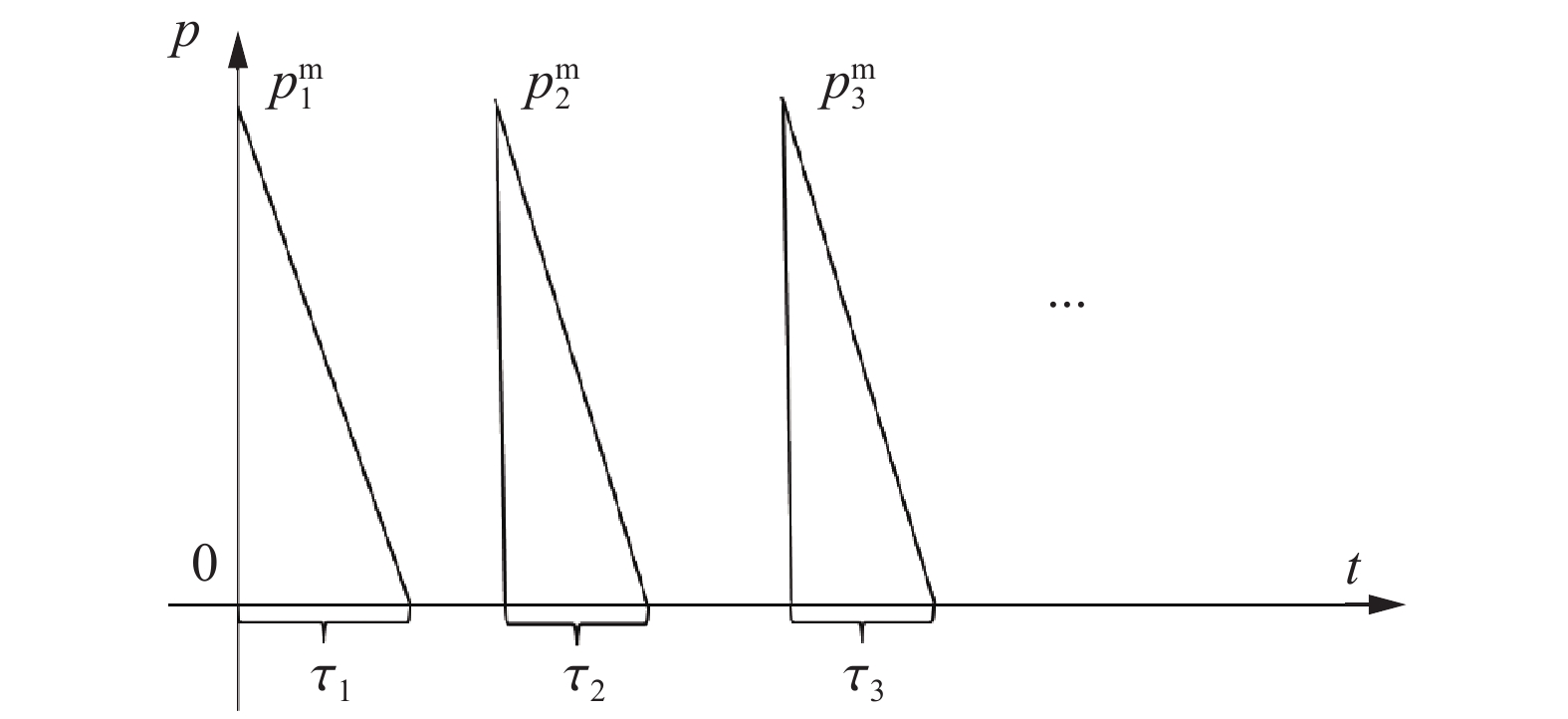
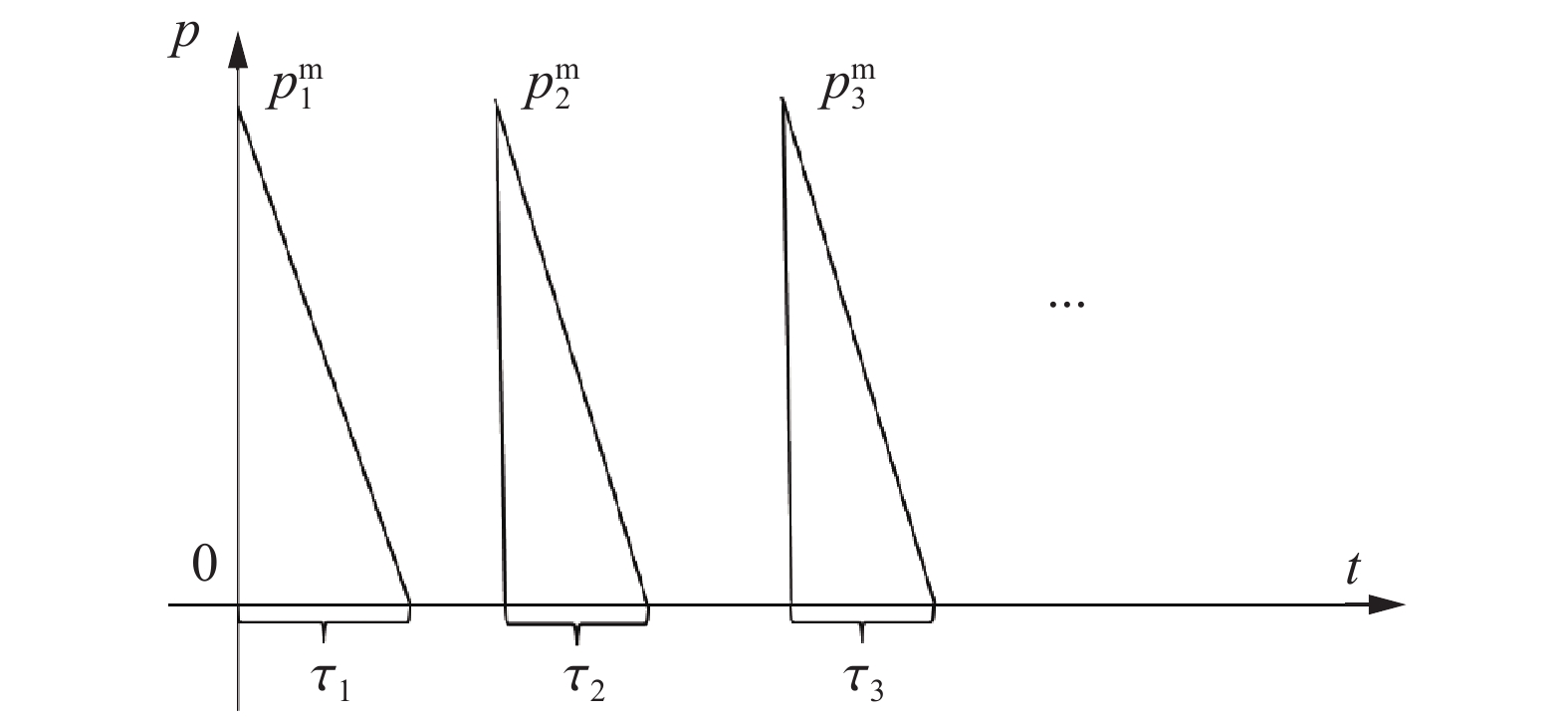
摘要: 针对固支圆板在多次远场空爆载荷下的位移响应问题，基于膜理论能量方程，提出一种理论建模方法：通过将多次空爆载荷简化为线性衰减脉冲序列，首次建立了考虑应变率强化效应与累积硬化效应的固支圆板位移响应理论模型。首次加载阶段采用线性位移场近似，后续加载阶段引入二次函数位移场假设，推导出多次爆炸下中点位移的递推公式。LS-Dyna二次、三次空爆数值模拟验证表明，理论解与模拟结果的误差分别为20%~30%和20%以下。理论模型表明，圆板中点位移可表征为末次爆炸单独位移与前期累积位移的加权平方根函数，且后期爆炸的位移增量随前期累积位移增大而减小。
- 多次爆炸 /
- 固支圆板 /
- 累积损伤 /
- 位移场 /
- 远场空爆 /
- 膜理论
Abstract: Regarding the displacement response of clamped circular plates under multiple far-field blast loads, we proposes a novel theoretical modeling approach based on membrane theory energy equations, by simplifying multiple blast loads into linearly decaying pulse sequences, a theoretical displacement response model for clamped circular plates is established for the first time, considering both strain rate strengthening effects and cumulative hardening effects. The linear displacement field approximation is adopted for the initial loading phase, while a quadratic function displacement field assumption is introduced for subsequent loading phases, deriving recursive formulas for midpoint displacements under multiple blasts. Numerical validations were conducted using LS-DYNA for both double and triple blast scenarios. For double blast cases, theoretical predictions exhibited errors of 20%–30% compared to simulation results, while errors reduced to below 20% for triple blast conditions. The ASTM A415 steel circular plate model was used for the simulations, and the strain rate strengthening effect was described by the Cowper-Symonds model. Finite element models with quadrilateral shell elements demonstrated strong agreement with experimental data (errors<10%), confirming model reliability. The assumption of quadratic function displacement field for subsequent loading phases was verified by numerical displacement curves of the middle profiles of the plates. Further parametric analysis proved that the theoretical model is effective for different tangent modulus, which represents the strength of the strain strengthening effect. The model reveals that midpoint displacement can be characterized as a weighted square root function combining the final explosion’s individual displacement and prior cumulative displacement, with displacement increments from subsequent explosions decreasing as prior cumulative displacement increases.
- multiple blast /
- clamped plate /
- cumulative damage /
- displacement field /
- far-field air blast /
- membrane theory

HTML全文

图 1 多次载荷示意图

Figure 1. Schematic diagram of multiple loads

下载: 全尺寸图片幻灯片

图 2 线性强化刚塑性模型

Figure 2. Linear strengthening rigid plastic model

下载: 全尺寸图片幻灯片

图 3 圆板空爆仿真有限元模型

Figure 3. Finite element model for the circular plate under blast loads

下载: 全尺寸图片幻灯片

图 4 单次空爆载荷下圆板中点位移的实验、数值模拟与理论结果的对比

Figure 4. Comparison of theoretical, test, and simulation result of midpoint displacement of the circular plate under single blast loads

下载: 全尺寸图片幻灯片

图 5 6 N·s+6 N·s冲量组合加载条件下圆板位移场

Figure 5. Displacement field of circular plate under 6 N·s+6 N·s impulse combination

下载: 全尺寸图片幻灯片

图 6 不同冲量组合加载条件下圆板中点位移时间曲线

Figure 6. Time curves of midpoint displacement of the circular plate under different impulse combinations

下载: 全尺寸图片幻灯片

图 7 典型二次空爆载荷下圆板中剖面位移曲线比较图

Figure 7. Comparison of displacement curves of middle profile of the circular plate under typical two blast loads

下载: 全尺寸图片幻灯片

图 8 典型三次空爆载荷下圆板中剖面位移曲线比较图（第3次加载后中剖面位移曲线）

Figure 8. Comparison of displacement curves of middle profile of the circular plate under typical three blast loads. (Displacement curve of the middle profile after the third loading)

下载: 全尺寸图片幻灯片

表 1 圆板尺寸与材料参数^[17]

Table 1. Size and material parameters of the circular plate

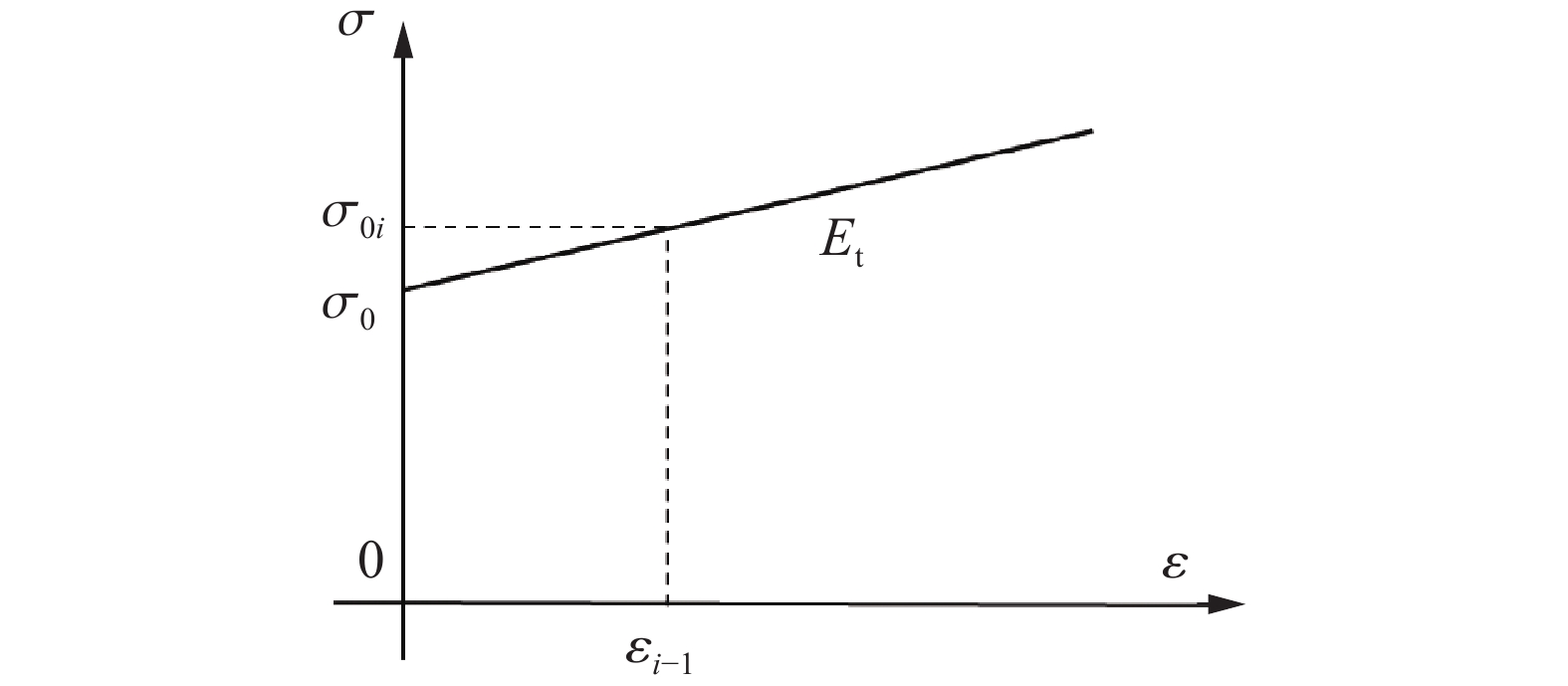
R/mm	H/mm	ρ/(kg·m⁻³)	$ {\dot{\varepsilon }}_{0} $/s⁻¹	n	σ₀/MPa	E_t/MPa
31.8	1.93	7800	40	5	223	10.8

下载: 导出CSV

表 2 实验与数值模拟结果对比

Table 2. Comparison of numerical and experimental results

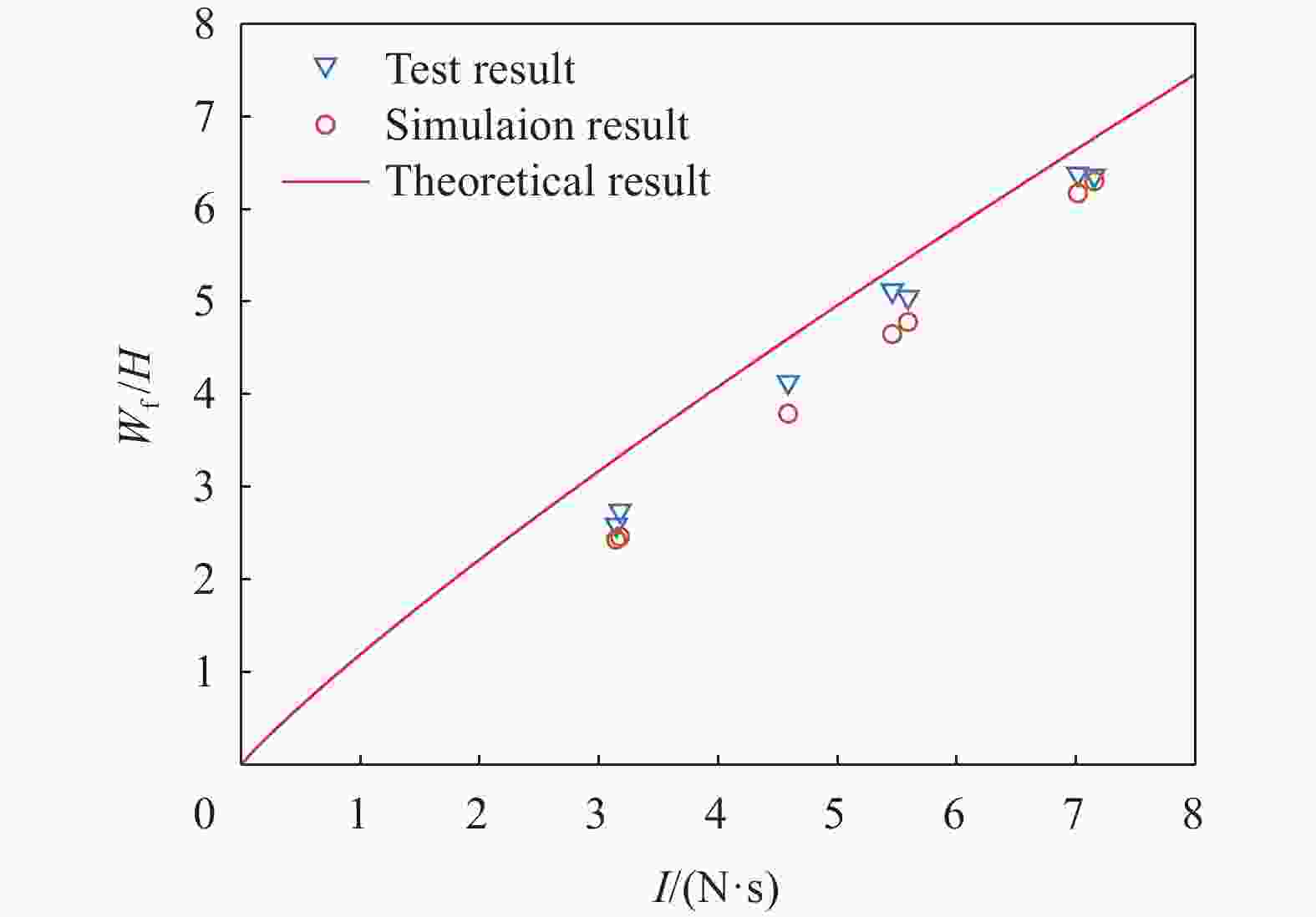
序号	实验数据^[16]		模拟数据
序号	I_t/(N·s)	W_f/H	p^m/MPa	τ/ms	W_f/mm	W_f/H	(W_f/H误差)/%
1	7.153	6.36	450.313	0.01	12.16	6.30	−0.94
2	3.145	2.59	197.991	0.01	4.69	2.43	−6.18
3	5.458	5.12	343.605	0.01	8.97	4.65	−9.18
4	5.591	5.05	351.978	0.01	9.22	4.78	−5.35
5	3.176	2.74	199.943	0.01	4.74	2.46	−10.22
6	4.586	4.13	288.709	0.01	7.32	3.79	−8.23
7	7.015	6.38	441.625	0.01	11.91	6.17	−3.29

下载: 导出CSV

表 3 二次空爆载荷下圆板中点位移理论与模拟结果的比较

Table 3. Comparison between theoretical and numerical results of midpoint displacement of the circular plate under two blast loads

冲量/(N·s)	$ W_{1}^{\mathrm{f}} $/mm		$ W_{1}^{\mathrm{f}} $误差/%	$ W_{2}^{\mathrm{f}} $/mm			$ W_{2}^{\mathrm{f}} $误差/%
冲量/(N·s)	模拟	理论	$ W_{1}^{\mathrm{f}} $误差/%	模拟	理论	修正理论	理论	修正理论
3+3	4.43	6.12	38.15	5.49	8.65	7.65	57.56	39.34
3+4	4.43	6.12	38.15	6.37	9.97	8.50	56.51	33.44
3+5	4.43	6.12	38.15	7.72	11.36	9.43	47.15	22.15
3+6	4.43	6.12	38.15	9.25	12.77	10.40	38.05	12.43
4+3	6.24	7.88	26.12	6.95	9.97	9.11	43.45	31.08
4+4	6.24	7.88	26.12	7.50	11.14	9.84	48.40	31.20
4+5	6.24	7.88	26.12	8.30	12.39	10.65	49.28	28.31
4+6	6.24	7.88	26.12	9.43	13.70	11.52	45.28	22.16
5+3	8.10	9.57	18.02	8.62	11.36	10.61	31.67	23.09
5+4	8.10	9.57	18.02	8.94	12.39	11.24	38.59	25.73
5+5	8.10	9.57	18.02	9.34	13.53	11.95	44.75	27.94
5+6	8.10	9.57	18.02	10.11	14.74	12.73	45.70	25.91
6+3	9.99	11.22	12.11	10.47	12.77	12.10	21.87	15.57
6+4	9.99	11.22	12.11	10.74	13.70	12.66	27.47	17.88
6+5	9.99	11.22	12.11	11.09	14.74	13.30	32.82	19.93
6+6	9.99	11.22	12.11	11.50	15.85	14.00	37.74	21.74

下载: 导出CSV

表 4 三次空爆载荷下圆板中点位移理论与模拟结果的比较（$E_{\mathrm{t}}=10.8\;{\mathrm{MPa}} $）

Table 4. Comparison between theoretical and numerical results of midpoint displacement of the circular plate under three blast loads ($E_{\mathrm{t}}=10.8\;{\mathrm{MPa}} $)

冲量/(N·s)	$ W_{1}^{\mathrm{f}} $/mm		$ W_{1}^{\mathrm{f}} $误差/%	$ W_{2}^{\mathrm{f}} $/mm		$ W_{2}^{\mathrm{f}} $误差/%	$ W_{3}^{\mathrm{f}} $/mm		$ W_{3}^{\mathrm{f}} $误差/%
冲量/(N·s)	模拟	理论	$ W_{1}^{\mathrm{f}} $误差/%	模拟	理论	$ W_{2}^{\mathrm{f}} $误差/%	模拟	理论	$ W_{3}^{\mathrm{f}} $误差/%
3+3+3	4.43	6.12	38.15	5.49	7.65	39.34	6.76	8.92	31.95
4+4+4	6.24	7.87	26.12	7.50	9.84	31.20	9.42	11.48	21.87
5+5+5	8.10	9.56	18.02	9.34	11.95	27.94	11.79	13.94	18.24
6+6+6	9.99	11.20	12.11	11.50	14.00	21.74	15.17	16.33	7.65
4+5+6	6.24	7.87	26.12	8.30	10.65	28.31	11.84	13.57	14.61
4+6+5	6.24	7.87	26.12	9.43	11.52	22.16	12.37	13.57	9.70
5+4+6	8.10	9.56	18.02	8.94	11.24	25.73	12.00	14.03	16.92
5+6+4	8.10	9.56	18.02	10.11	12.73	25.91	11.81	14.03	18.80
6+4+5	9.99	11.20	12.11	10.74	12.66	17.88	12.07	14.55	20.55
6+5+4	9.99	11.20	12.11	11.09	13.30	19.93	12.20	14.55	19.26

下载: 导出CSV

表 5 三次空爆载荷下圆板中点位移理论与模拟结果的比较（$E_{\mathrm{t}}=2\;{\mathrm{GPa}} $）

Table 5. Comparison between theoretical and numerical results of midpoint displacement of the circular plate under three blast loads ($E_{\mathrm{t}}=2\;{\mathrm{GPa}} $)

冲量/(N·s)	$ W_{1}^{\mathrm{f}} $/mm		$ W_{1}^{\mathrm{f}} $误差/%	$ W_{2}^{\mathrm{f}} $/mm		$ W_{2}^{\mathrm{f}} $误差/%	$ W_{3}^{\mathrm{f}} $/mm		$ W_{3}^{\mathrm{f}} $误差/%
冲量/(N·s)	模拟	理论	$ W_{1}^{\mathrm{f}} $误差/%	模拟	理论	$ W_{2}^{\mathrm{f}} $误差/%	模拟	理论	$ W_{3}^{\mathrm{f}} $误差/%
3+3+3	4.18	5.70	36.36	5.33	7.14	33.96	5.78	8.27	43.08
4+4+4	5.85	7.04	20.34	6.68	8.87	32.78	8.36	10.25	22.61
5+5+5	7.45	8.18	9.80	8.46	10.37	22.58	10.10	11.98	18.61
6+6+6	9.02	9.16	1.55	10.08	11.70	16.07	12.36	13.52	9.39
4+5+6	5.85	7.04	20.34	7.51	9.62	28.10	10.78	12.00	11.32
4+6+5	5.85	7.04	20.34	8.50	10.41	22.47	10.59	12.02	13.50
5+4+6	7.45	8.18	9.80	7.95	9.72	22.26	10.27	12.07	17.53
5+6+4	7.45	8.18	9.80	9.10	11.08	21.76	10.33	12.09	17.04
6+4+5	9.02	9.16	1.55	9.37	10.49	11.95	10.51	12.08	14.94
6+5+4	9.02	9.16	1.55	9.70	11.07	14.12	10.35	12.08	16.71

下载: 导出CSV

参考文献(17)

[1]	JONES N. Structural impact [M]. 2nd ed. New York: Cambridge University Press, 2012.
[2]	HENCHIE T F, YUEN S C K, NURICK G N, et al. The response of circular plates to repeated uniform blast loads: an experimental and numerical study [J]. International Journal of Impact Engineering, 2014, 74: 36–45. DOI: 10.1016/j.ijimpeng.2014.02.021.
[3]	周游, 纪冲, 王雷元, 等. 重复爆炸载荷作用下薄壁方管动力响应研究 [J]. 兵工学报, 2019, 40(9): 1871–1880. DOI: 10.3969/j.issn.1000-1093.2019.09.012. ZHOU Y, JI Y, WANG L Y, et al. Research on the dynamic response of thin-walled square tube under repeated blast loads [J]. Acta Armamentarii, 2019, 40(9): 1871–1880. DOI: 10.3969/j.issn.1000-1093.2019.09.012.
[4]	张斐, 张春辉, 张磊, 等. 多次水下爆炸作用下钢板动态响应数值模拟 [J]. 中国舰船研究, 2019, 14(6): 122–129. DOI: 10.19693/j.issn.1673-3185.01431. ZHANG F, ZHANG C H, ZHANG L, et al. Numerical simulation of dynamic response of steel plate subjected to multiple underwater explosions [J]. Chinese Journal of Ship Research, 2019, 14(6): 122–129. DOI: 10.19693/j.issn.1673-3185.01431.
[5]	张斐, 张春辉, 张磊, 等. 多次水下爆炸作用下钢板与焊接钢板冲击损伤特性 [J]. 振动与冲击, 2020, 39(7): 196–201. DOI: 10.13465/j.cnki.jvs.2020.07.027. ZHANG F, ZHANG C H, ZHANG L, et al. Impact damage of steel plate and welding steel plate under multiple underwater explosions [J]. Journal of Vibration and Shock, 2020, 39(7): 196–201. DOI: 10.13465/j.cnki.jvs.2020.07.027.
[6]	李旭东, 尹建平, 杜志鹏, 等. 多次水下爆炸钢制圆板应变与挠度增长规律分析 [J]. 振动与冲击, 2020, 39(5): 131–136. DOI: 10.13465/j.cnki.jvs.2020.05.017. LI X D, YIN J P, DU Z P, et al. Growth law analysis for strain and deflection of steel circular plates subjected to multiple underwater explosions [J]. Journal of Vibration and Shock, 2020, 39(5): 131–136. DOI: 10.13465/j.cnki.jvs.2020.05.017.
[7]	ZIYA-SHAMAMI M, BABAEI H, MOSTOFI T M, et al. Structural response of monolithic and multi-layered circular metallic plates under repeated uniformly distributed impulsive loading: an experimental study [J]. Thin-Walled Structures, 2020, 157: 107024. DOI: 10.1016/j.tws.2020.107024.
[8]	李锡锋. 多次内爆加载下舰船舱室结构毁伤效应研究 [D]. 太原: 中北大学, 2021. DOI: 10.27470/d.cnki.ghbgc.2021.001010. LI X F. Research on damage effect of ship cabin structure under multiple implosion [D]. Taiyuan: North University of China, 2021. DOI: 10.27470/d.cnki.ghbgc.2021.001010.
[9]	NASIRI S, SADEGH-YAZDI M, MOUSAVI S M, et al. Repeated underwater explosive forming: experimental investigation and numerical modeling based on coupled Eulerian-Lagrangian approach [J]. Thin-Walled Structures, 2022, 172: 108860. DOI: 10.1016/j.tws.2021.108860.
[10]	唐正鹏, 李翔宇, 郑监. 多次水下爆炸中船体梁的累积毁伤效应 [J]. 高压物理学报, 2022, 36(2): 025102. DOI: 10.11858/gywlxb.20210809. TANG Z P, LI X Y, ZHENG J. Cumulative damage effect of hull girder subjected to multiple underwater explosions [J]. Chinese Journal of High Pressure Physics, 2022, 36(2): 025102. DOI: 10.11858/gywlxb.20210809.
[11]	唐正鹏, 李翔宇. 多次水下爆炸对船体梁累积毁伤试验研究 [J]. 水下无人系统学报, 2022, 30(3): 364–370, 377. DOI: 10.11993/j.issn.2096-3920.2022.03.012. TANG Z P, LI X Y. Experiments on cumulative damage to hull girders subjected to multiple underwater explosions [J]. Journal of Unmanned Undersea Systems, 2022, 30(3): 364–370, 377. DOI: 10.11993/j.issn.2096-3920.2022.03.012.
[12]	TIAN W J, ZHAI H B, LIU Y S, et al. A response prediction method for clamped circular plates subjected to repeated blast loading [J]. International Journal of Impact Engineering, 2023, 180: 104684. DOI: 10.1016/j.ijimpeng.2023.104684.
[13]	黄鑫华, 李应刚, 张永峰, 等. 多次水下爆炸下背空加筋板损伤累积特性研究 [J]. 舰船科学技术, 2023, 45(19): 9–16. DOI: 10.3404/j.issn.1672-7649.2023.19.002. HUANG X H, LI Y G, ZHANG Y F, et al. Research on damage accumulation characteristic of air-backed stiffened plate subjected to multiple underwater explosions [J]. Ship Science and Technology, 2023, 45(19): 9–16. DOI: 10.3404/j.issn.1672-7649.2023.19.002.
[14]	张文超. 多发武器水下爆炸作用下结构毁伤特性及冲击环境研究 [D]. 哈尔滨: 哈尔滨工程大学, 2022. DOI: 10.27060/d.cnki.ghbcu.2022.001456. ZHANG W C. Research on structural damage characteristics and impact environment of multiple weapons exploded underwater [D]. Harbin: Harbin Engineering University, 2022. DOI: 10.27060/d.cnki.ghbcu.2022.001456.
[15]	LI X Y, LIANG M Z, TIAN Z D, et al. Dynamic response and cumulative damage mechanism of simplified hull girders under repeated underwater explosions [J]. Thin-Walled Structures, 2024, 196: 111554. DOI: 10.1016/j.tws.2023.111554.
[16]	BODNER S R, SYMONDS P S. Experiments on viscoplastic response of circular plates to impulsive loading [J]. Journal of the Mechanics and Physics of Solids, 1979, 27(2): 91–113. DOI: 10.1016/0022-5096(79)90013-9.
[17]	WEI Q Y, WANG Z, SHI D Y, et al. Method based on the membrane theory for equivalence between arbitrarily shaped pressure pulse applied on circular plate and rectangular pressure pulse [J]. International Journal of Impact Engineering, 2023, 179: 104658. DOI: 10.1016/j.ijimpeng.2023.104658.