孔隙坍塌行为对多孔材料冲击压缩特性的影响理论分析

马路遥; 张先锋; 熊玮; 刘闯; 谈梦婷; 邓宇轩; 侯先苇

doi:10.11883/bzycj-2024-0502

孔隙坍塌行为对多孔材料冲击压缩特性的影响理论分析

doi: 10.11883/bzycj-2024-0502

南京理工大学机械工程学院，江苏南京 210094

基金项目: 国家自然科学基金项目（12141202，12202205）

详细信息

作者简介:
马路遥（2001－　），男，博士研究生，3501093819@qq.com

通讯作者:
张先锋（1978－　），男，博士，教授，lynx@njust.edu.cn

中图分类号: O346.3
计量
- 文章访问数: 141
- HTML全文浏览量: 8
- PDF下载量: 32
- 被引次数: 0
出版历程
- 网络出版日期: 2025-03-05

Theoretical analysis of the influence of pore collapse behavior on the shock compression characteristics of porous materials

School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China

摘要

摘要: 多孔材料在冲击压缩过程中伴随着孔隙坍塌行为，本文基于前人开展的试验中所观测到的冲击波结构，对多孔材料的冲击波形成过程及孔隙坍塌行为间的联系进行了理论分析。首先，考虑多孔材料的压缩曲线特性和冲击波追赶问题，提出了多孔材料的冲击波结构存在低压单波模式、双冲击波模式和高压单波三种模式。进一步，结合Wu-Jing物态方程发展了与不同冲击波模式相容的冲击压缩特性计算方法，得到了与单冲击波模式相容的冲击比容计算方程，可以无需采取近似条件直接计算临界比容。此外，通过对弹性阶段与弹塑性阶段材料的孔隙度随压力的变化规律采取线性近似，并考虑了多孔材料中基体材料受力与宏观应力之间的关系，修正了Carroll建立的孔隙坍塌关系方程。基于本文发展的考虑孔隙坍塌行为的冲击压缩特性计算模型，对材料的Hugoniot数据进行了计算，讨论了孔隙坍塌行为对多孔材料冲击压缩特性的影响。结果表明在较低压力时材料的冲击物态特性受孔隙坍塌行为影响明显，本文模型能够更加精确地预测多孔材料的冲击波参量。
- 多孔材料 /
- 爆炸力学 /
- Wu-Jing方程 /
- 冲击波结构 /
- 孔隙坍塌
Abstract: Porous materials are accompanied by pore collapse behavior during impact compression. Based on the shock wave structure observed in experiments carried out by predecessors, the theoretically analysis of the relationship between the shock wave formation process and pore collapse behavior of porous materials is made. Firstly, considering the compression curve characteristics of porous materials and the overtaking of shock wave, it is proposed that the shock wave structure of porous materials has three modes: low pressure single wave mode, double shock wave mode and high pressure single wave mode. These different shock wave modes are mainly caused by the influence of elastic-plastic mechanical behavior in pore collapse on the compression curve of porous materials. Furthermore, combined with the Wu-Jing equation of state, the calculation method of shock compression characteristics compatible with different shock wave modes is developed. The relationship between the Hugoniot Curve of porous material and dense material is established, and the calculation equation of impact specific volume compatible with single shock wave mode is obtained, which can directly calculate the critical specific volume without approximate conditions. In addition, the equation of pore collapse established by Carroll is modified by taking the linear approximation of the variation of porosity with pressure in the elastic stage and the elastic-plastic stage, and considering the relationship between the stress of the matrix material and the macroscopic stress in the porous material. Based on the calculation model of shock compression characteristics considering pore collapse behavior, the Hugoniot data of the material are calculated, and the influence of pore collapse behavior on the shock compression characteristics of porous materials is discussed. The results show that the shock compression characteristics of the material are significantly affected by the pore collapse behavior at lower pressures, and the model in this paper can predict the shock wave parameters of porous materials more accurately.
- porous material /
- mechanics of explosion /
- Wu-Jing model /
- shock wave structure /
- pore collapse

HTML全文

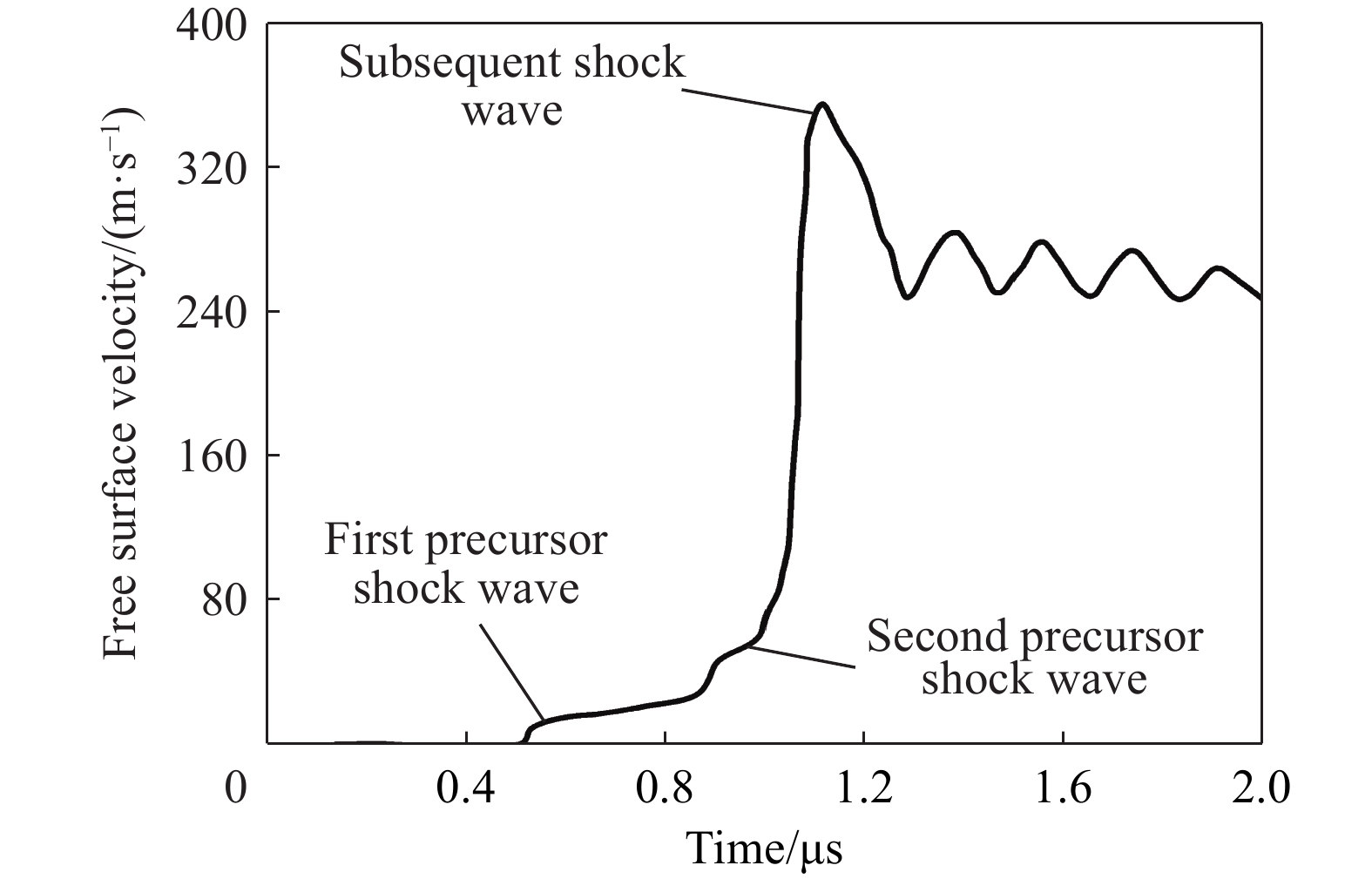
图 1 典型的具有三波结构的波剖面^[18]

Figure 1. Typical wave profile with three-wave structure

下载: 全尺寸图片幻灯片

图 2 具有三波结构的多孔材料冲击波波剖面示意图

Figure 2. Schematic diagram of shock wave profile of porous material with three-wave structure

下载: 全尺寸图片幻灯片

图 3 不同压缩曲线的材料在压缩过程中的波系特征示意图

Figure 3. The schematic diagram of wave system characteristics of materials with different compression curves in the process of compression

下载: 全尺寸图片幻灯片

图 4 多孔材料冲击绝热线示意图

Figure 4. Schematic diagram of Hugoniot curve of porous material

下载: 全尺寸图片幻灯片

图 5 多孔材料简化模型冲击绝热线示意图

Figure 5. Schematic diagram of Hugoniot curve of porous material in Simplified mode

下载: 全尺寸图片幻灯片

图 6 冲击波追赶问题示意图

Figure 6. Characteristic line diagram of shock wave overtaking problem

下载: 全尺寸图片幻灯片

图 7 多孔材料中的三种冲击波模式

Figure 7. Three shock wave modes in porous materials

下载: 全尺寸图片幻灯片

图 8 三种计算方式下Hugoniot数据计算结果与实验结果对比

Figure 8. Comparison of the experimental results and computation of Hugoniot data under three calculation methods

下载: 全尺寸图片幻灯片

图 9 不同的孔隙坍塌模型下前驱冲击波波速与试验结果^{[15, 16]}的对比

Figure 9. Comparison of precursor shock wave velocity with experimental results under different pore collapse models

下载: 全尺寸图片幻灯片

图 10 多孔钨的不同屈服强度下前驱冲击波波速与剪切模量及初始孔隙度的关系

Figure 10. The relationship between precursor shock wave velocity and shear modulus and initial porosity under different yield strength

下载: 全尺寸图片幻灯片

图 11 不同屈服强度下多孔铜Hugoniot数据计算结果与实验结果对比

Figure 11. Comparison of the experimental results and computation of Hugoniot data of porous copper under different yield strength

下载: 全尺寸图片幻灯片

图 12 不同初始孔隙度下多孔铁Hugoniot数据计算结果与实验结果对比

Figure 12. Comparison of the experimental results and computation of Hugoniot data of porous iron under different initial porosity

下载: 全尺寸图片幻灯片

表 1 计算密实材料Hugoniot数据所需的材料常数

Table 1. The material constants required for dense materials to calculate Hugoniot data

材料 ρ₀(g/cm³) Q(Gpa) q σ_y(Gpa) G(Gpa)

铜 8.924 52.90 10.0696 0.6^[27] 47.7^[27]

钨 19.2 185.27 7.1086 2.2^[27] 160^[27]

铁 7.856 34.94 11.9378 0.68^[28] 89^[28]

下载: 导出CSV

参考文献(29)

[1]	余同希. 关于“多胞材料”和“点阵材料”的一点意见 [J]. 力学与实践, 2005, 27(3): 90. DOI: 10.6052/1000-0992-2004-387. YU T X. Some Comments on 'Cellular Materials' and 'Lattice Materials' [J]. Mechanics in Engineering, 2005, 27(3): 90. DOI: 10.6052/1000-0992-2004-387.
[2]	EVANS A G , HUTCHINSON J W , ASHBY M F . Multifunctionality of cellular metal systems[J]. Progress in Materials Science, 1998, 43(3): 171-221. DOI: 10.1016/S0079-6425(98)00004-8.
[3]	张锦明, 张合, 戴可人, 等. 多孔弹性复合材料研制及其吸能缓冲特性 [J]. 兵工学报, 2022(001): 043. DOI: 10.3969/j.issn.1000-1093.2022.01.017. ZHANG J M, ZHANG H, DAI K R, et al. Preparation of Elastic Porous Composite Material and Its Energy-absorption Characteristics [J]. Acta Armamentarii, 2022(001): 043. DOI: 10.3969/j.issn.1000-1093.2022.01.017.
[4]	李西军, 周显明, 经福谦. 一种多孔铁的高压声速和冲击熔化 [J]. 高压物理学报, 2001(02): 117–121. DOI: CNKI:SUN:GYWL.0.2001-02-006. LI X J, ZHOU X M, JING F Q. Sound Speed of A Kind Of Porous Iron at High Pressures [J]. Chinese Journal of High Pressure Physics, 2001(02): 117–121. DOI: CNKI:SUN:GYWL.0.2001-02-006.
[5]	MCQUEEN R G, MARSH S P. Equation of State for Nineteen Metallic Elements from Shock‐Wave Measurements to Two Megabars [J]. Journal of Applied Physics, 1960, 31(7): 1253–1269. DOI: 10.1063/1.1735815.
[6]	OH K H, PERSSON P A. Equation of state for extrapolation of high‐pressure shock Hugoniot data [J]. Journal of Applied Physics, 1989, 65(10): 3852–3856. DOI: 10.1063/1.343434.
[7]	QIANG W, FUQIAN J. Thermodynamic equation of state and application to Hugoniot predictions for porous materials [J]. Journal of Applied Physics, 1996, 80(8): 4343–4349. DOI: 10.1063/1.363391.
[8]	李欣竹, 吴强. 一种体积物态方程物理基础的讨论 [J]. 高压物理学报, 2001, 15(2): 155–160. DOI: 10.11858/gywlxb.2001.02.014. LI X Z, WU Q. The Physic Base of The New Equation of State [J]. Chinese Journal of High Pressure Physics, 2001, 15(2): 155–160. DOI: 10.11858/gywlxb.2001.02.014.
[9]	BOSHOFF M L, VILJOEN H J. Comparative study of analytical methods for Hugoniot curves of porous materials [J]. Journal of Applied Physics, 1999, 86(3): 1245–1254. DOI: 10.1063/1.370878.
[10]	GENG H Y, WU Q, TAN H, et al. Extension of the Wu-Jing equation of state for highly porous materials: Calculations to validate and compare the thermoelectron model [J]. Journal of Applied Physics, 2002, 92(10): 5917–5923. DOI: 10.1063/1.1516618.
[11]	耿华运, 吴强, 谭华. 热力学物态方程参数的统计力学表示 [J]. 物理学报, 2001, 50(7): 2. DOI: 10.3321/j.issn:1000-3290.2001.07.027. GENG H Y, WU Q, TAN H. Statistical Parameter of Thermodynamic Equation of State [J]. Acta Physica Sinica., 2001, 50(7): 2. DOI: 10.3321/j.issn:1000-3290.2001.07.027.
[12]	ZHANG X F, QIAO L, SHI A S, et al. A cold energy mixture theory for the equation of state in solid and porous metal mixtures [J]. Journal of Applied Physics, 2011, 110(1): 013506. DOI: 10.1063/1.3603018.
[13]	ZHOU Q, CHEN P, MA D, et al. A model used for Hugoniot prediction of material at high-temperature along isobaric path [J]. Journal of Applied Physics, 2013, 114(2): 023509. DOI: 10.1063/1.4813482.
[14]	WU B, WANG X, SUI H, et al. Shock compression of porous copper containing helium: Molecular dynamics simulations and theoretical model [J]. International Journal of Plasticity, 2024, 174: 103899. DOI: 10.1016/j.ijplas.2024.103899.
[15]	BOADE R R. Dynamic compression of porous tungsten [J]. Journal of Applied Physics, 1969, 40(9): 3781–3785. DOI: 10.1063/1.1658272.
[16]	BOADE R R. Principal Hugoniot, second-shock Hugoniot, and release behavior of pressed copper powder [J]. Journal of Applied Physics, 1970, 41(11): 4542–4551. DOI: 10.1063/1.1658494.
[17]	DOLGOBORODOV A, ROSTILOV T, ANANEV S, et al. Structure of Shock Wave in Nanoscale Porous Nickel at Pressures up to 7 GPa [J]. Materials, 2022, 15(23): 8501. DOI10.3390/ma15238501.
[18]	WANG Y G, HE H L, QI M L, et al. Time-resolved dynamic compaction and tensile fracture of low-porosity aluminum under impact loading [J]. Journal of Applied Physics, 2007(7): 102. DOI: 10.1063/1.2787160.
[19]	BONNAN S, HEREIL P L, COLLOMBET F. Experimental characterization of quasi static and shock wave behavior of porous aluminum [J]. Journal of Applied Physics, 1998, 83(11): 5741–5749. DOI: 10.1063/1.367430.
[20]	BODRENKO S I, KRYSANOV Y A, NOVIKOV S A. Propagation of shock waves in foamed polystyrene [J]. Journal of Applied Mechanics and Technical Physics, 1979, 20(6): 771–775. DOI: 10.1007/BF00908673.
[21]	OGORODNIKOV V A, IVANOV A G, ERUNOV S V, et al. Shock-wave deformation and fracture of zirconium dioxide ceramics of various fractional composition and porosity [J]. Combustion Explosion and Shock Waves, 2001, 37(6): 717–722. DOI: 10.1007/BF02673292.
[22]	蒋招绣. 多孔Pb(Zr_(0.95)Ti_(0.05))O_3铁电陶瓷的力学性能及失效行为研究[D]. 宁波大学, 97−99. DOI: CNKI:CDMD:1.1018.797492.
[23]	CARROLL M M, HOLT A C. Static and dynamic pore-collapse relations for ductile porous materials [J]. Journal of Applied Physics, 1972, 43(4): 1626-1636. DOI10.1063/1.1661372.
[24]	经福谦. 实验物态方程导引 [M]. 第2版. 北京: 科学出版社, 1999: 1-200.
[25]	HERRMANN W. Constitutive equation for the dynamic compaction of ductile porous materials [J]. Journal of Applied Physics, 1969, 40(6): 2490–2499. DOI: 10.1063/1.1658021.
[26]	JOHNSON J N. Dynamic fracture and spallation in ductile solids [J]. Journal of Applied Physics, 1981, 52(4): 2812–2825. DOI: 10.1063/1.329011.
[27]	STEINBERG D J, COCHRAN S G, GUINAN M W. A constitutive model for metals applicable at high-strain rate [J]. Journal of Applied Physics, 1980, 51(3): 1498–1504. DOI: 10.1063/1.327799.
[28]	陆景德 , 张万甲, 张玉松. 2#纯铁和不锈钢的变形硬化效应[J]. 爆炸与冲击, 1984(2): 75–79. LU J D , ZHANG W J , ZHANG Y S. Deformation hardening effect of 2 # pure iron and stainless steel [J]. Explosion and Shock Waves, 1984(2): 75–79.
[29]	BUTCHER B M, KARNES C H. Dynamic compaction of porous iron [J]. Journal of Applied Physics, 1969, 40(7): 2967–2976. DOI: 10.1063/1.1658109.