深海水下爆炸冲击波载荷及气泡脉动特性研究

杜青松; 刘云龙

doi:10.11883/bzycj-2024-0515

深海水下爆炸冲击波载荷及气泡脉动特性研究

doi: 10.11883/bzycj-2024-0515

杜青松^{1, 2},
刘云龙^{1, 2, ,}

1.
哈尔滨工程大学三亚南海创新发展基地，海南三亚 572024
2.
哈尔滨工程大学船舶工程学院，黑龙江哈尔滨 150001

基金项目: 国家自然科学基金（52088102）

详细信息

作者简介:
杜青松（2000－　），男，硕士研究生

通讯作者:
刘云龙（1988－　），男，博士，教授，yunlong_liu@hrbeu.edu.cn

中图分类号: O383
计量
- 文章访问数: 384
- HTML全文浏览量: 38
- PDF下载量: 103
- 被引次数: 0
出版历程
- 收稿日期: 2024-12-30
- 修回日期: 2025-07-30
- 网络出版日期: 2025-08-12

Research on the shock wave load and bubble pulsation characteristics of deep-sea underwater explosions

DU Qingsong^{1, 2},
LIU Yunlong^{1, 2
, ,}

1.
Nanhai Innovation & Development Center, Harbin Engineering University, Sanya 572024, Hainan, China
2.
College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, Heilongjiang, China

摘要

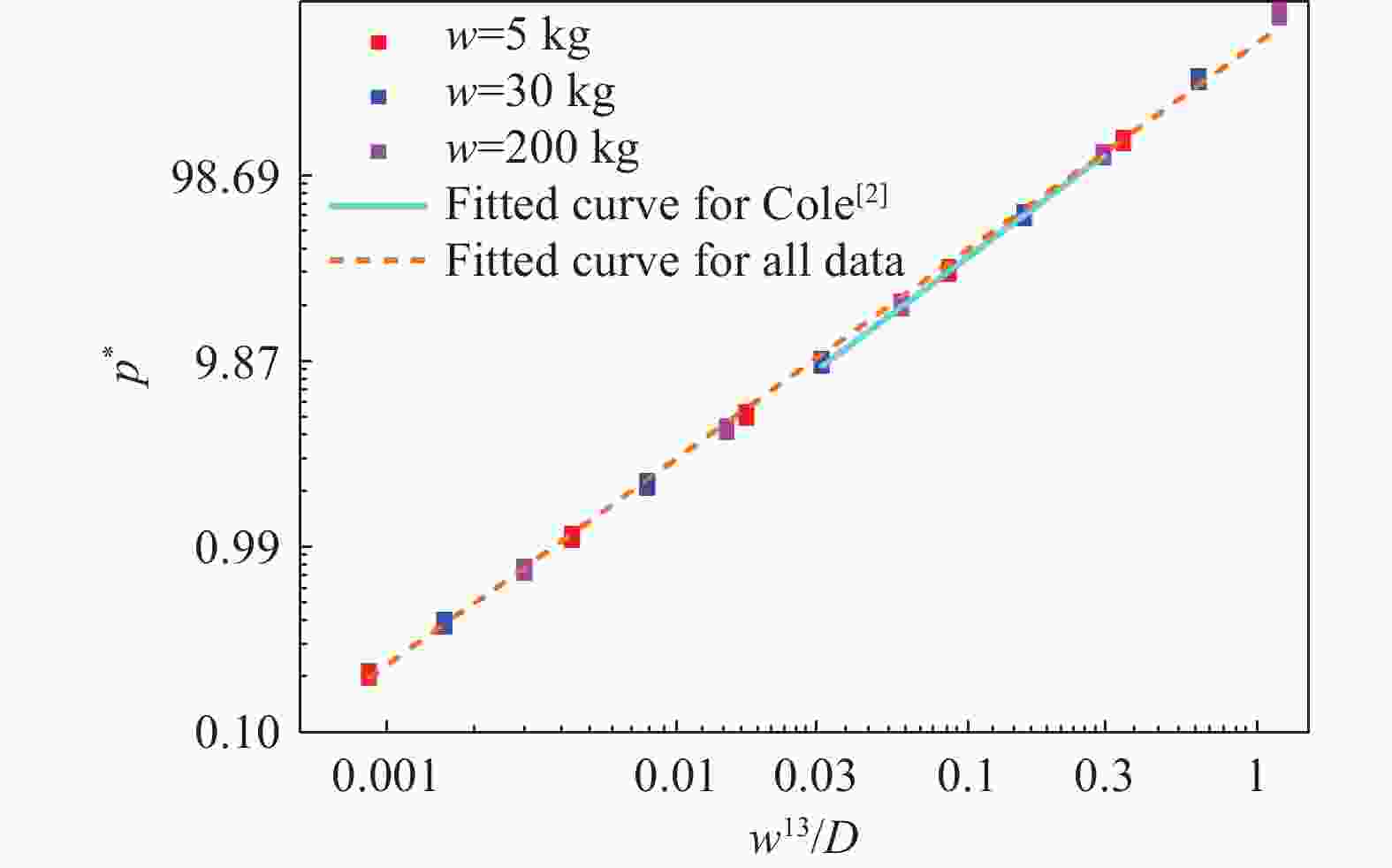
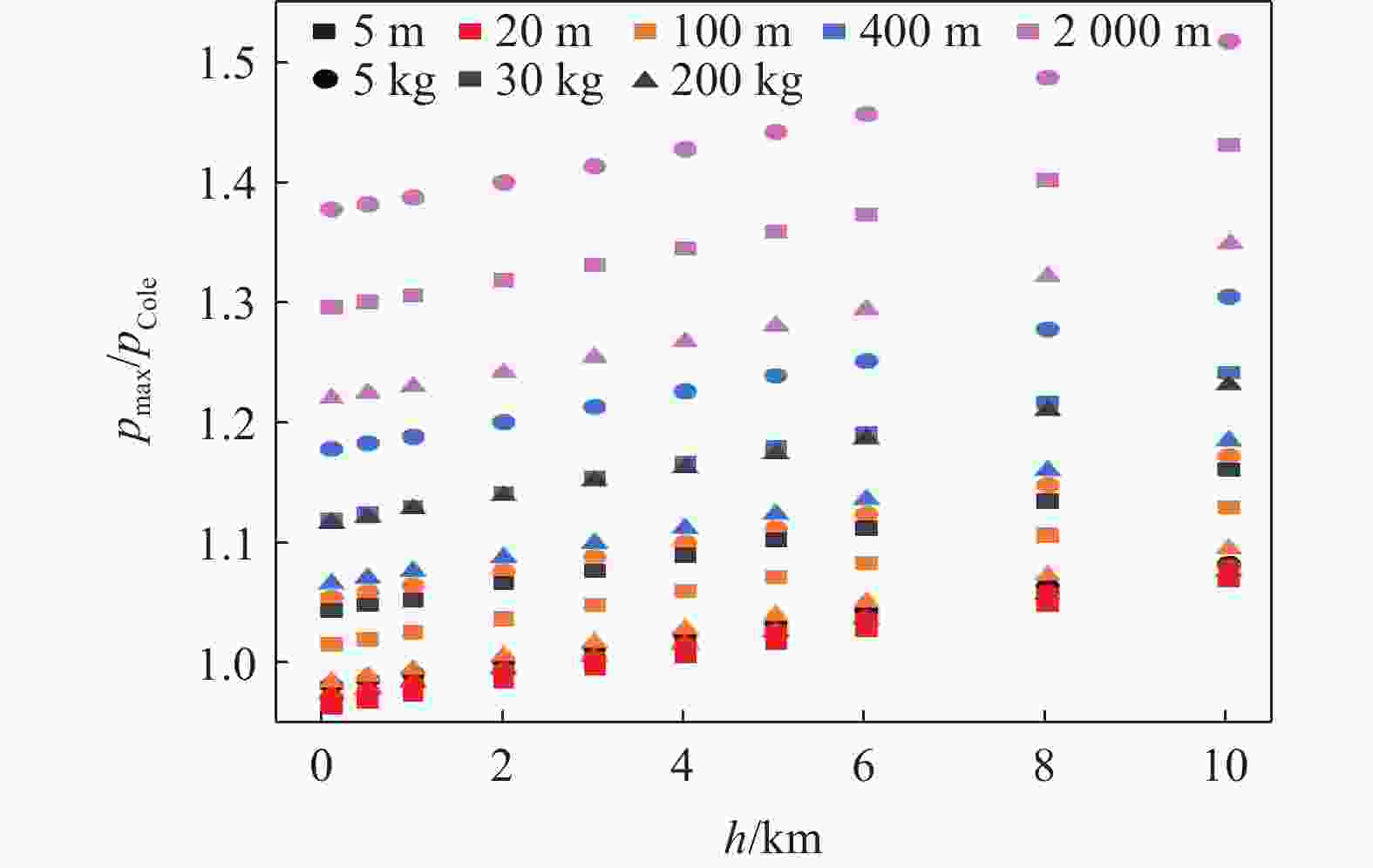
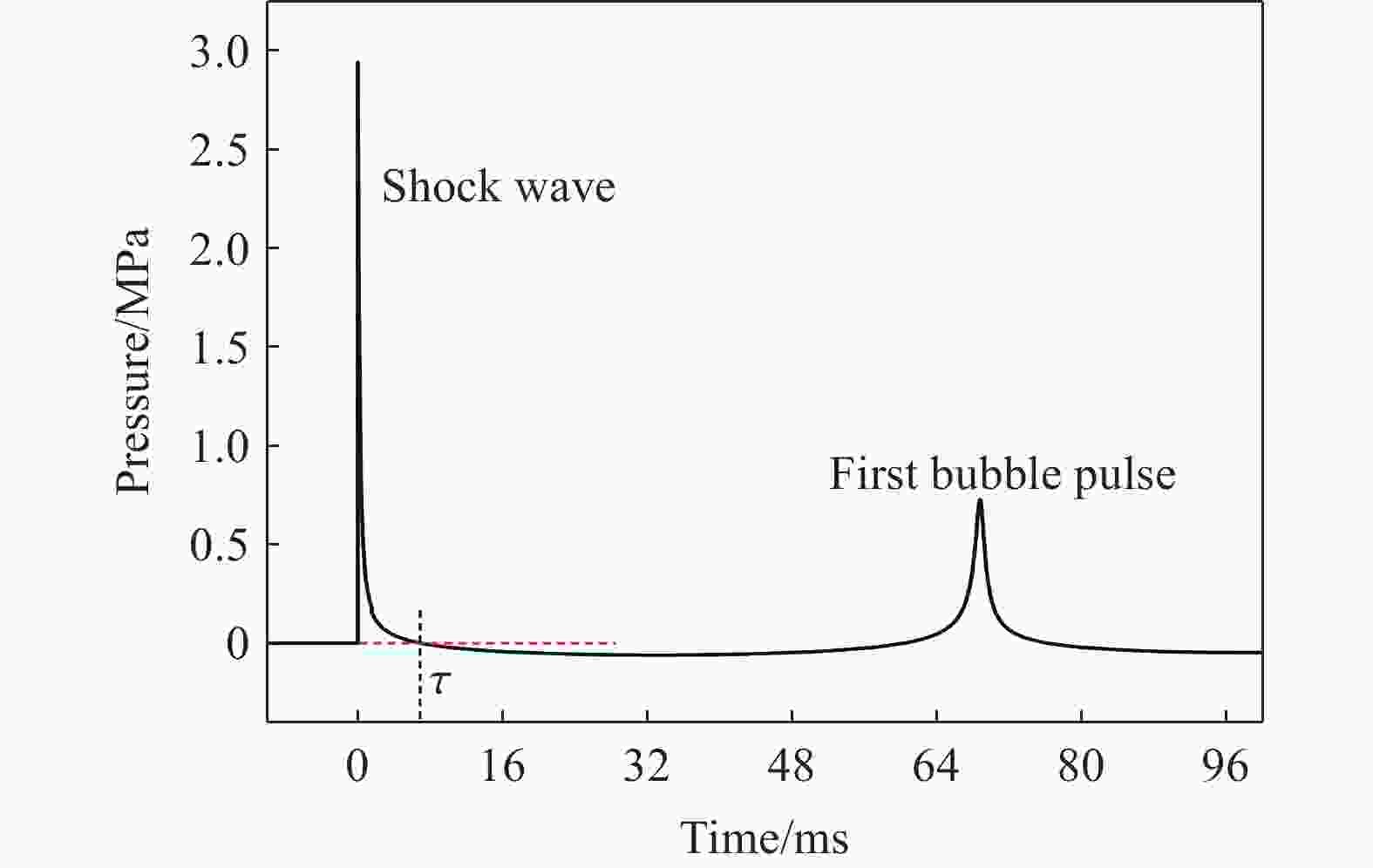
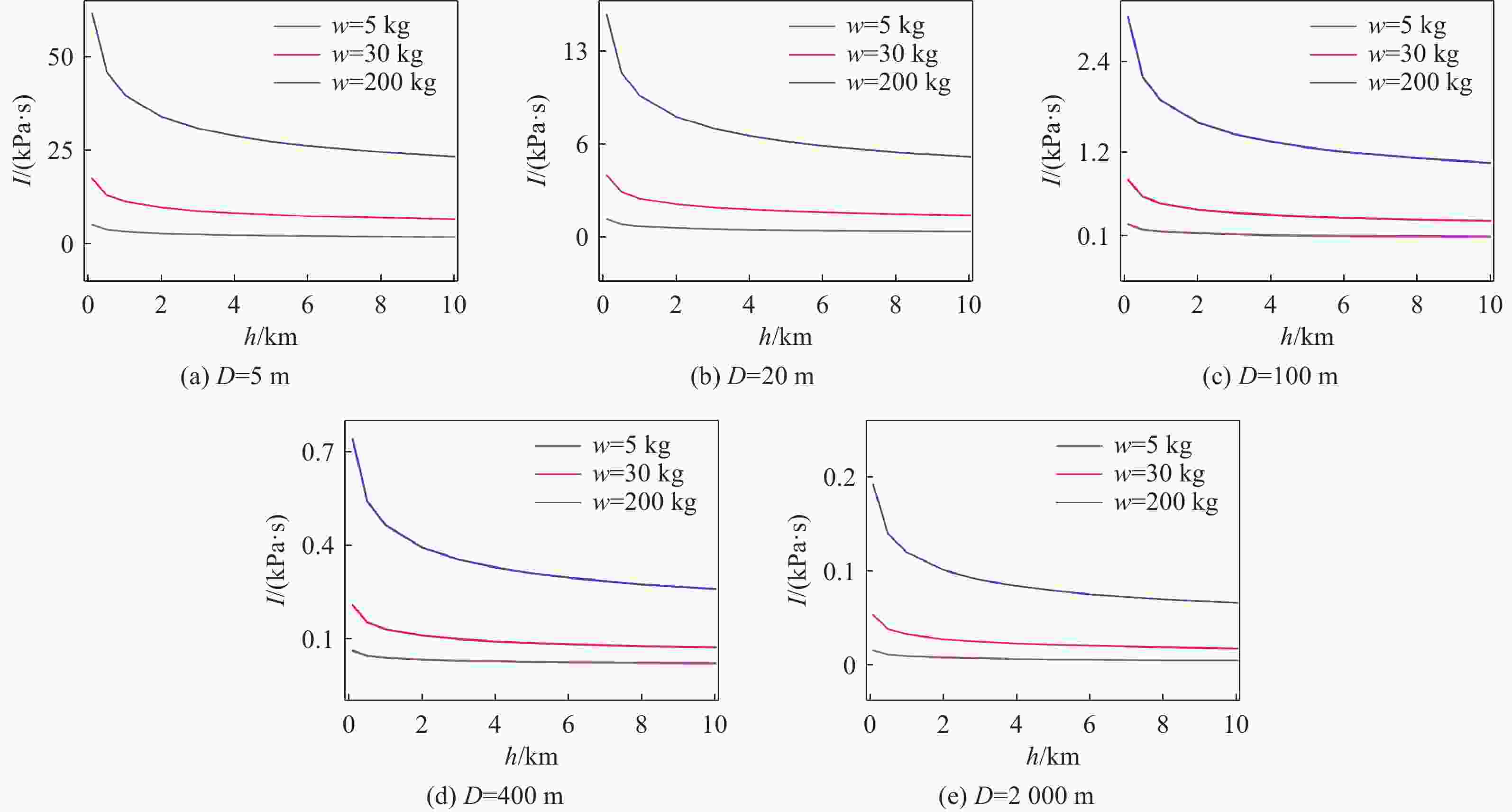
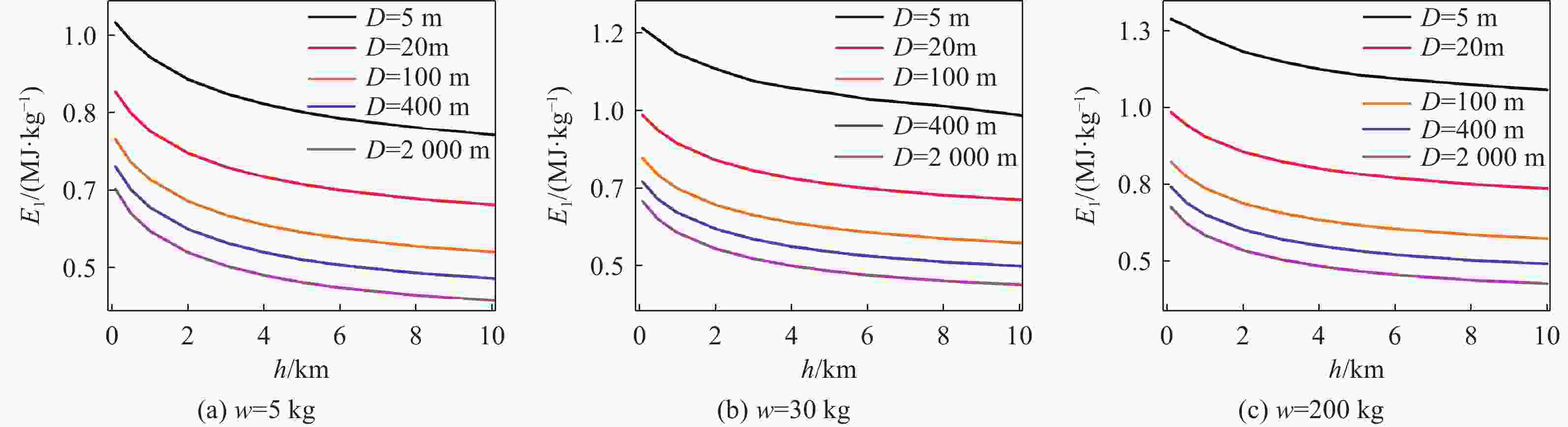
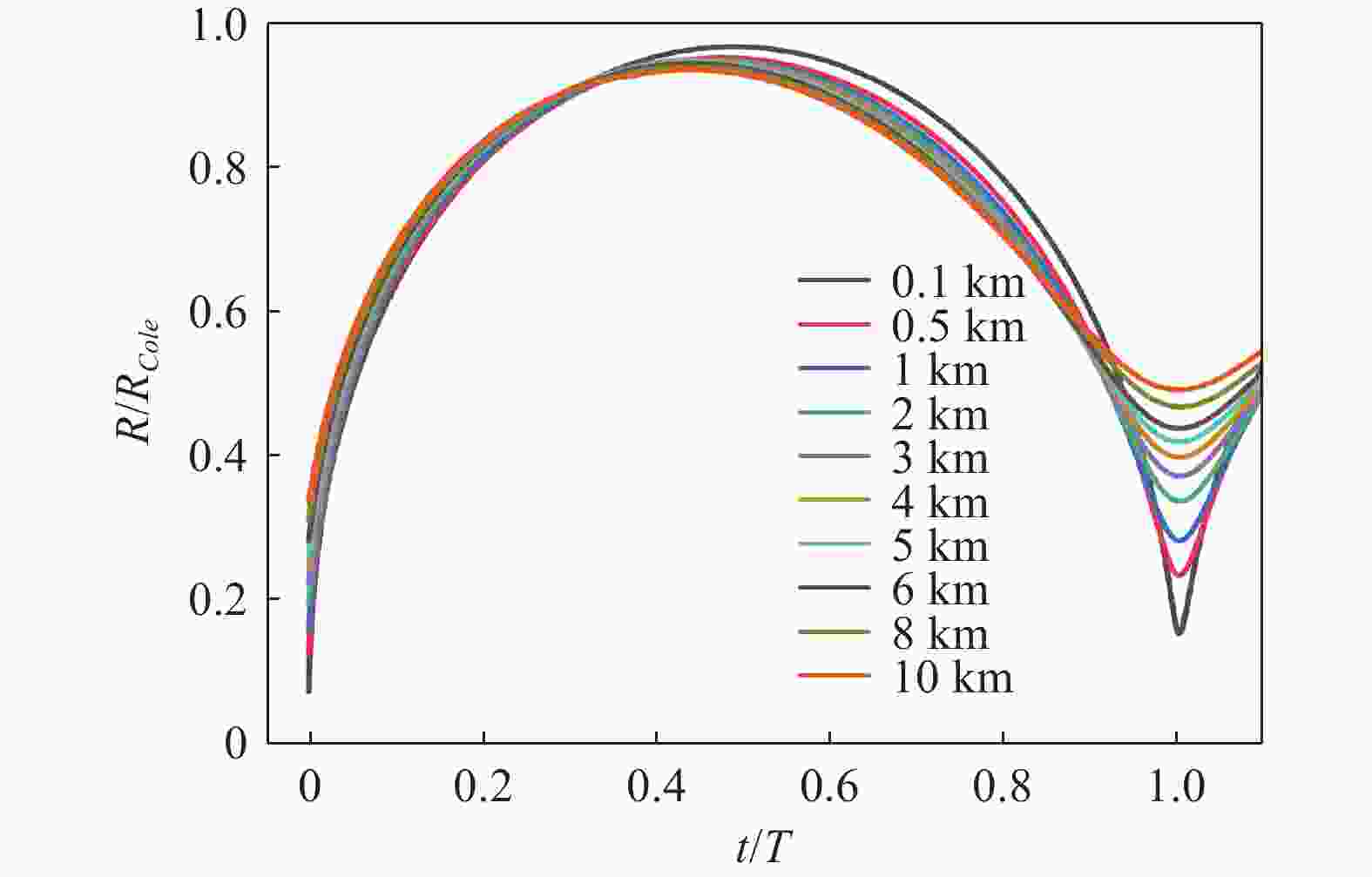
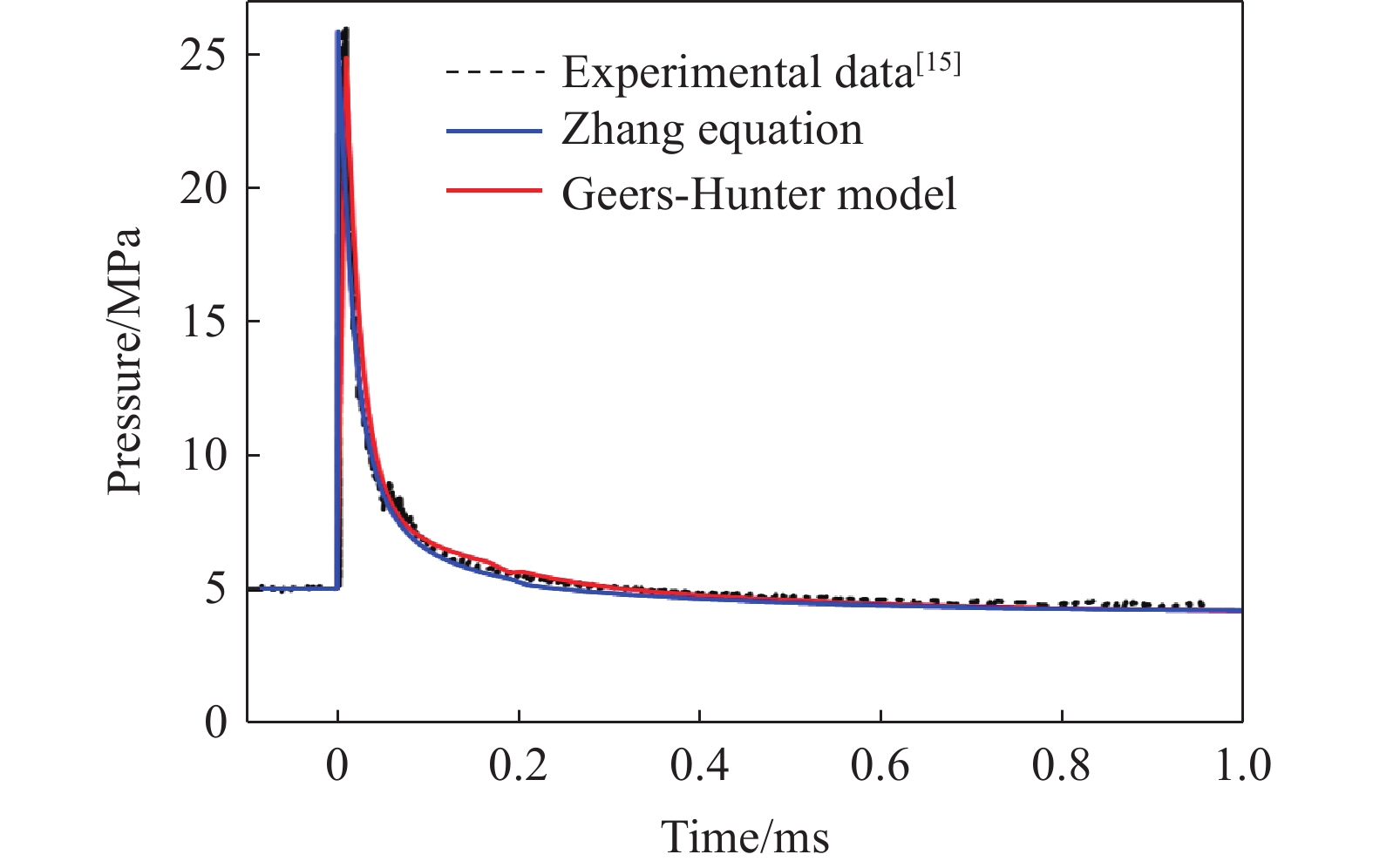
摘要: 深海水下爆炸中的冲击波载荷和气泡脉动规律因其极端环境的复杂性，在理论与试验研究中面临诸多挑战。针对深海水下爆炸现象，基于气泡统一方程理论模型，使用数值模拟的方式开展了不同水深、爆距和装药量的工况下水下爆炸冲击波和气泡脉动研究。结果表明，冲击波压力峰值主要受装药量与爆距影响，并随水深增加而略有上升，平均增长率约为每千米1%。冲击波冲量与比冲击波能在水深和爆距增大时呈下降趋势，但与装药量呈正相关关系。气泡脉动半径则主要由装药量和水深共同决定，在深水环境气泡脉动现象减弱。相较于传统Cole经验公式，模拟所得气泡脉动半径在0.1~10 km范围内有所减小。此外，气泡在一个完整脉动周期内的膨胀阶段持续时间普遍略长于坍缩阶段。
- 深海爆炸 /
- 冲击波 /
- 气泡脉动 /
- 气泡统一方程
Abstract: Underwater explosions in deep-sea environments involve complex interactions, making both theoretical modeling and experimental validation particularly challenging. While previous research has provided valuable insights into the basic features of shock wave propagation and bubble dynamics in underwater explosions, most existing studies are limited to shallow water scenarios or narrowly defined environmental parameters. Systematic research on the laws governing shock wave loads from deep-sea explosions and their associated bubble pulsation under varying operational conditions holds critical academic significance. Numerical simulations were conducted utilizing a zoned solution algorithm for shock waves derived from the unified equation for bubble dynamics theoretical model. The algorithm enabled numerical simulation of shock wave peak pressure and pressure attenuation processes under diverse initial conditions. Comparative analysis with experimental data confirmed model reliability, demonstrating a mere 0.5% deviation between simulated and measured peak pressures and excellent agreement in pressure attenuation processes. The simulations specifically investigated the influence of water depth, stand-off distance, and explosive charge mass on the peak pressure of the underwater explosion shock wave and explored the variation patterns of the shock wave under different initial conditions through an in-depth analysis of the shock wave impulse and specific shock wave energy. Furthermore, employing the same theoretical model, the bubble pulsation characteristics within a single cycle under varying water depths and explosive charge masses were comparatively analyzed. Traditional empirical formulas were employed to analyze the numerical simulation results, and dimensionless treatment was conducted on the parameters. The results reveal that the peak pressure of the shock wave is primarily influenced by the charge mass and stand-off distance, and increases with water depth at an approximate rate of 1% per kilometer. In contrast, both shock wave impulse and specific shock wave energy decrease with increasing water depth and stand-off distance, but show a positive correlation with charge magnitude. The bubble pulse radius is primarily determined by both the charge weight and the water depth, with the bubble pulsation phenomenon becoming attenuated in deep-water environments. Compared to the traditional Cole empirical formula, the simulated bubble pulse radius is reduced in the range of 0.1 to 10 km. The simulation indicates an asymmetry in the pulsation cycle: the expansion phase consistently lasts slightly longer than the collapse phase. These findings contribute to a more nuanced understanding of underwater explosion phenomena in deep-sea environments and have practical implications for naval engineering, subsea structural safety assessment, and explosive ordnance disposal in complex oceanic settings.
- deep-sea explosion /
- shock wave /
- bubble pulsation /
- unified bubble equation

HTML全文

图 1 设定工况下数值模拟结果与试验结果^[15]对比

Figure 1. Comparison of numerical simulation results and experimental results^[15] under specified conditions

下载: 全尺寸图片幻灯片

图 2 数值模拟与经验公式^[2]的计算结果无量纲拟合关系

Figure 2. Fitting relationship between dimensionless calculation results of numerical simulation and empirical formulas^[2]

下载: 全尺寸图片幻灯片

图 3 基于数值模拟与经验公式^[2]的无量纲冲击波峰值压力随水深变化

Figure 3. Variation trend of dimensionless peak shock wave pressure with water depth based on numerical simulation and empirical formulation^[2]

下载: 全尺寸图片幻灯片

图 4 冲击波从压力峰值衰减至0所需要的时间

Figure 4. Time required for the shock wave to decay from its pressure peak to zero

下载: 全尺寸图片幻灯片

图 5 在不同装药质量、爆距和水深的工况下基于Zhang方程计算得到的冲量变化

Figure 5. Variation of shock wave impulse under different charge masses, stand-off distances, and water depths based on Zhang equation simulation

下载: 全尺寸图片幻灯片

图 6 不同装药量、爆距和水深的工况下基于Zhang方程计算得到的比冲击波能变化

Figure 6. Variation of specific shock wave energy under different charge masses, stand-off distances, and water depths based on Zhang equation simulation

下载: 全尺寸图片幻灯片

图 7 不同水深条件下Zhang方程模拟的气泡无量纲脉动半径单周期内变化趋势

Figure 7. Variation of dimensionless bubble radius during single oscillation cycle in Zhang equation simulations across different water depths

下载: 全尺寸图片幻灯片

表 1 TNT炸药的材料初始参数

Table 1. Material initial parameters of TNT

A/GPa B/GPa R₁ R₂ ω

371.2 3.231 4.15 0.95 0.3

下载: 导出CSV

表 2 Zhang方程计算工况

Table 2. Calculation Conditions of Zhang Equation

TNT装药量w/kg 爆距D/m 水深h/km

5 5、20、100、
400、2000 0.1、0.5、1、2、3、
4、5、6、8、10

30

200

下载: 导出CSV

参考文献(28)

[1]	TAYLOR G I. The formation of a blast wave by a very intense explosion Ⅰ. Theoretical discussion [J]. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 1950, 201(1065): 159–174. DOI: 10.1098/rspa.1950.0049.
[2]	COLE R H, WELLER R. Underwater explosions [J]. Physics Today, 1948, 1(6): 35. DOI: 10.1063/1.3066176.
[3]	SEDOV L I, FRIEDMAN M, HOLT M, et al. Similarity and dimensional methods in mechanics [J]. Journal of Applied Mechanics, 1982, 28(1): 159. DOI: 10.1115/1.3640458.
[4]	ARONS A B. Underwater Explosion Shock Wave Parameters at large distances from the charge [J]. The Journal of the Acoustical Society of America, 1954, 26(3): 343–346. DOI: 10.1121/1.1907339.
[5]	BJARNHOLT G. Suggestions on standards for measurement and data evaluation in the underwater explosion test [J]. Propellants, Explosives, Pyrotechnics, 1980, 5(2-3): 67–74. DOI: 10.1002/prep.19800050213.
[6]	KEDRINSKII V K. Underwater explosions, shock tubes, and explosive sound sources[M]// Hydrodynamics of Explosion: Experiments and Models. Berlin, Heidelberg: Springer Berlin Heidelberg, 2005: 29–81. DOI: 10.1007/3-540-28563-6_3.
[7]	LE MÉHAUTÉ B, WANG S. Overview of the wave generation process and the wave field[M]// Water Waves Generated by Underwater Explosion: Volume 10. Singapore: World Scientific, 1996: 1–65. DOI: 10.1142/9789814350884_0001.
[8]	GEERS T L, HUNTER K S. An integrated wave-effects model for an underwater explosion bubble [J]. The Journal of the Acoustical Society of America, 2002, 111(4): 1584–1601. DOI: 10.1121/1.1458590.
[9]	PLESSET M S. The dynamics of cavitation bubbles [J]. Journal of Applied Mechanics, 1949, 16(3): 277–282. DOI: 10.1115/1.4009975.
[10]	KELLER J B, MIKSIS M. Bubble oscillations of large amplitude [J]. The Journal of the Acoustical Society of America, 1980, 68(2): 628–633. DOI: 10.1121/1.384720.
[11]	ZHANG A M, LI S M, CUI P, et al. A unified theory for bubble dynamics [J]. Physics of Fluids, 2023, 35(3): 033323. DOI: 10.1063/5.0145415.
[12]	ZHANG A M, LI S M, XU R, et al. A theoretical model for compressible bubble dynamics considering phase transition and migration [J]. Journal of Fluid Mechanics, 2024, 999: A58. DOI: 10.1017/jfm.2024.954.
[13]	SLIFKO J F. Pressure-pulse characteristics of deep explosions as functions of depth and range: NOLTR 67-87 [R]. White Oak, Maryland: United States Naval Ordnance Laboratory, 1967.
[14]	XIAO P, YANG K. Experimental results for peak pressure and sound exposure level in deep-sea explosions [J]. ACOUSTICS AUSTRALIA, 2015, 43(2): 175–178. DOI: 10.1007/s40857-015-0020-9.
[15]	GAO Y, WANG S, ZHANG J, et al. Effects of underwater explosion depth on shock wave overpressure and energy [J]. Physics of Fluids, 2022, 34(3): 037108. DOI: 10.1063/5.0081107.
[16]	GAO Y, WANG S, ZHANG J, et al. Influence of water depth on the peak overpressure and energy of the secondary pressure wave of underwater explosions [J]. Ocean Engineering, 2024, 293: 116580. DOI: 10.1016/j.oceaneng.2023.116580.
[17]	郝轶, 周章涛, 张显丕. 球型密闭容器内水下爆炸载荷特性研究 [J]. 兵工学报, 2015, 36(S1): 108–114. HAO Z, ZHOU Z T, ZHANG X T. The pressure characteristics of high pressure spherical closed container under underwater explosion [J]. Acta Armamentarii, 2015, 36(S1): 108–114.
[18]	梁浩哲, 杨莉, 张庆明. 深水条件下TNT炸药的爆炸特性 [J]. 兵工学报, 2016, 37(S2): 241–245. LIANG H Z, YANG L, YANG Q M. The explosive characteristics of TNT under deep water [J]. Acta Armamentarii, 2016, 37(S2): 241–245.
[19]	胡毅亭, 贾宪振, 饶国宁, 等. 水下爆炸冲击波和气泡脉动的数值模拟研究 [J]. 舰船科学技术, 2009, 31(2): 134–140. DOI: 10.3404/j.issn.1672-7649.2009.02.027. HU Y T, JIA X Z, RAO G N, et al. Numerical study of underwater explosion shock wave and bubble pulse [J]. Ship Science and Technology, 2009, 31(2): 134–140. DOI: 10.3404/j.issn.1672-7649.2009.02.027.
[20]	YUE J, WU X, HUANG C. Scaling law of deep-sea trinitrotoluene (TNT) explosion [J]. Acta Mechanica Sinica, 2024, 40(4): 123280. DOI: 10.1007/s10409-023-23280-x.
[21]	SHEN C, YAN B, PEI D, et al. Investigation of the shock wave load characteristics in deep-water explosions based on high-order compressible multiphase fluids [J]. Journal of Applied Physics, 2024, 136(12): 124702. DOI: 10.1063/5.0225697.
[22]	XIAO F, CHEN Y, HUA H, et al. Experimental and numerical investigation on the shock resistance of honeycomb rubber coatings subjected to underwater explosion [J]. Proceedings of the Institution of Mechanical Engineers, Part M: Journal of Engineering for the Maritime Environment, 2015, 229(1): 77–94. DOI: 10.1177/1475090213500244.
[23]	LIU Z H, IGLAND R. Numerical simulation of a subsea pipeline subjected to underwater explosion loads with the coupled Eulerian-Lagrangian method[C]// Volume 3: Materials Technology; Pipelines, Risers, and Subsea Systems. Hamburg, Germany: American Society of Mechanical Engineers, 2022: V003T04A028. DOI: 10.1115/OMAE2022-80657.
[24]	徐润泽, 唐皓, 李世民, 等. 基于气泡统一方程的水下爆炸气泡迁移特征参数影响规律研究 [J]. 力学学报, 2024, 56(9): 2544–2554. DOI: 10.6052/0459-1879-24-074. XU R Z, TANG H, LI S M, et al. Study on the influence of migration character parameters for underwater explosion bubbles based on the unified equation for bubble dynamics [J]. Chinese Journal of Theoretical and Applied Mechanics, 2024, 56(9): 2544–2554. DOI: 10.6052/0459-1879-24-074.
[25]	谈乃正, 詹立蕾, 李世民, 等. 基于气泡统一方程的声场双气泡耦合作用研究 [J]. 哈尔滨工程大学学报, 2024, 45(2): 213–222. DOI: 10.11990/jheu.202309033. TAN N Z, ZHAN L L, LI S M, et al. A study on the coupling effect of double bubbles in sound field based on the unified equation for bubble dynamics [J]. Journal of Harbin Engineering University, 2024, 45(2): 213–222. DOI: 10.11990/jheu.202309033.
[26]	SWISDAK M M, Jr. Explosion effects and properties: part Ⅱ. explosion effects in water: NSWC/WCL TR 76-116 [R]. Dahlgren, Virginia; Silver Spring, Maryland: Naval Surface Weapons Center, 1978. DOI: 10.21236/ADA056694.
[27]	张阿漫, 明付仁, 刘云龙, 等. 水下爆炸载荷特性及其作用下的舰船毁伤与防护研究综述 [J]. 中国舰船研究, 2023, 18(3): 139–154,196. DOI: 10.19693/j.issn.1673-3185.03273. ZHANG A M, MING F R, LIU Y L, et al. Review of research on underwater explosion related to load characteristics and ship damage and protection [J]. Chinese Journal of Ship Research, 2023, 18(3): 139–154,196. DOI: 10.19693/j.issn.1673-3185.03273.
[28]	马坤, 初哲, 王可慧, 等. 小当量炸药深水爆炸气泡脉动模拟实验 [J]. 爆炸与冲击, 2015, 35(3): 320–325. DOI: 10.11883/1001-1455-(2015)03-0320-06. MA K, CHU Z, WANG K H, et al. Experimental research on bubble pulse of small scale charge exploded under simulated deep water [J]. Explosion and Shock Waves, 2015, 35(3): 320–325. DOI: 10.11883/1001-1455-(2015)03-0320-06.