基于电磁Hopkinson杆系统的恒应力比动态拉伸/压缩-扭转复合试验装置及方法

杜冰; 岳一凡; 刘震; 丁翼; 王维斌; 刘琛琳; 郭亚洲; 李玉龙

doi:10.11883/bzycj-2025-0243

基于电磁Hopkinson杆系统的恒应力比动态拉伸/压缩-扭转复合试验装置及方法

doi: 10.11883/bzycj-2025-0243

西北工业大学航空学院，陕西西安 710072

基金项目: 国家重大科技专项（J2019-VIII-008-0169）；国家自然科学基金（U2241274，12261131505）；高等学校学科创新引智计划（BP0719007）

详细信息

作者简介:
杜　冰（1996－　），男，博士研究生，daniel_dubing@mail.nwpu.edu.cn

通讯作者:
李玉龙（1961－　），男，博士，教授，liyulong@nwpu.edu.cn

中图分类号: O347.3
计量
- 文章访问数: 125
- HTML全文浏览量: 22
- PDF下载量: 19
- 被引次数: 0
出版历程
- 收稿日期: 2025-08-10
- 修回日期: 2025-11-04
- 网络出版日期: 2025-11-13

Constant stress-ratio dynamic tension/compression-torsion testing device and method based on electromagnetic Hopkinson bar system

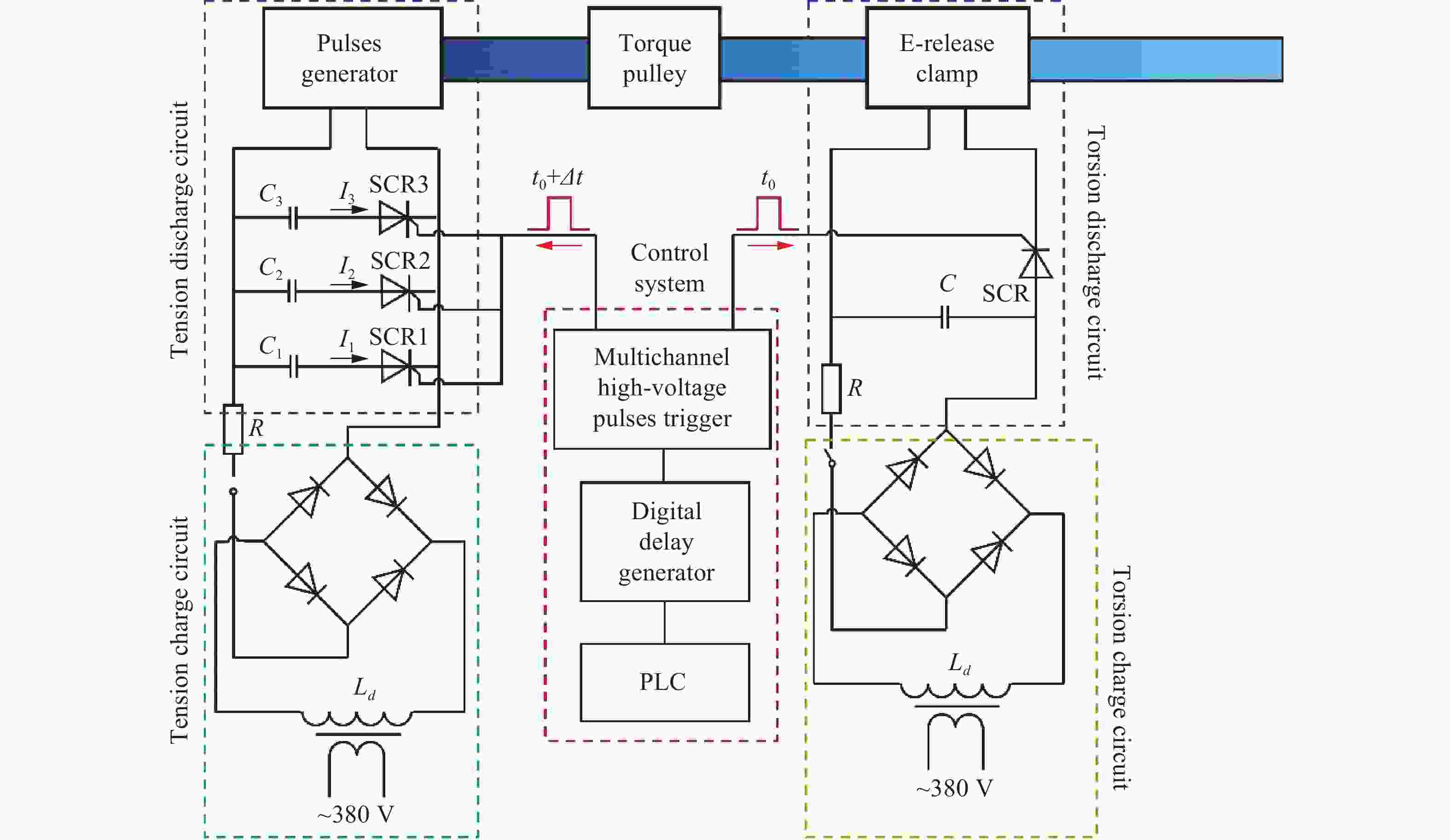
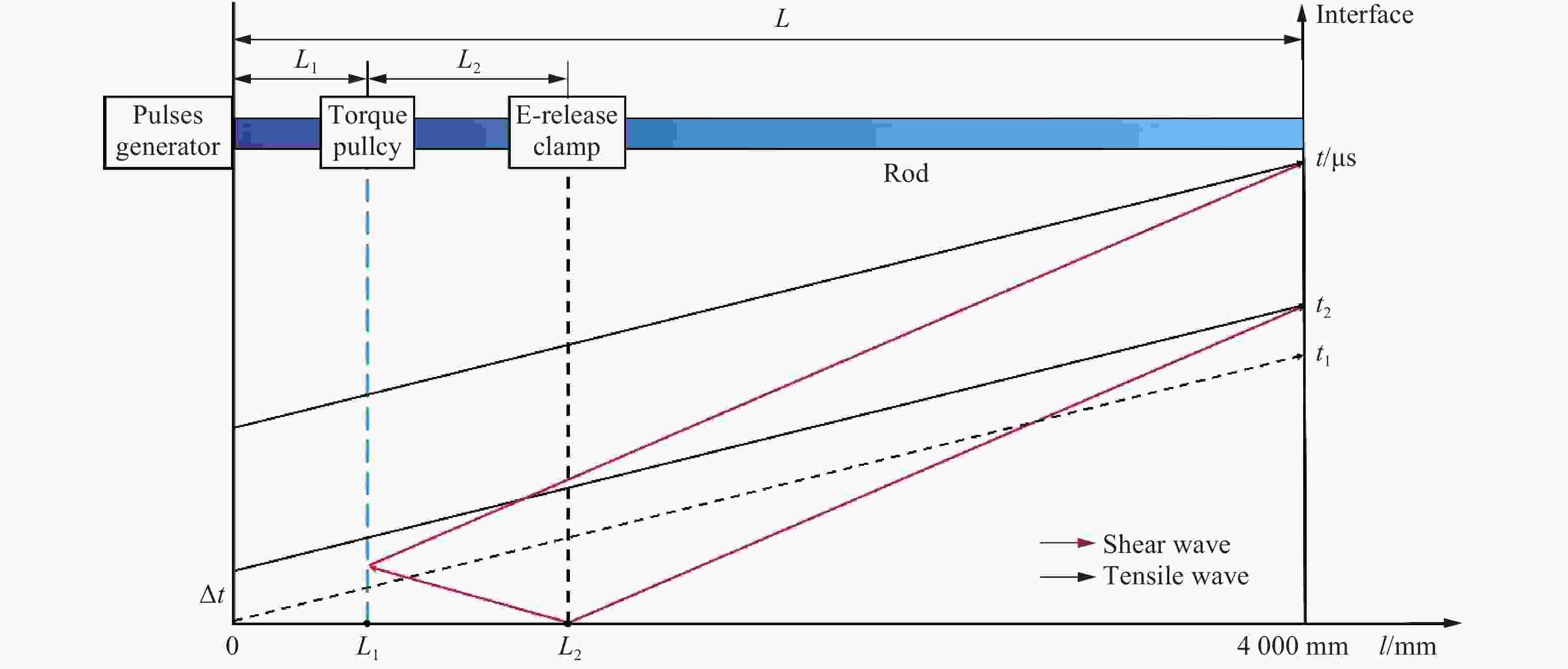
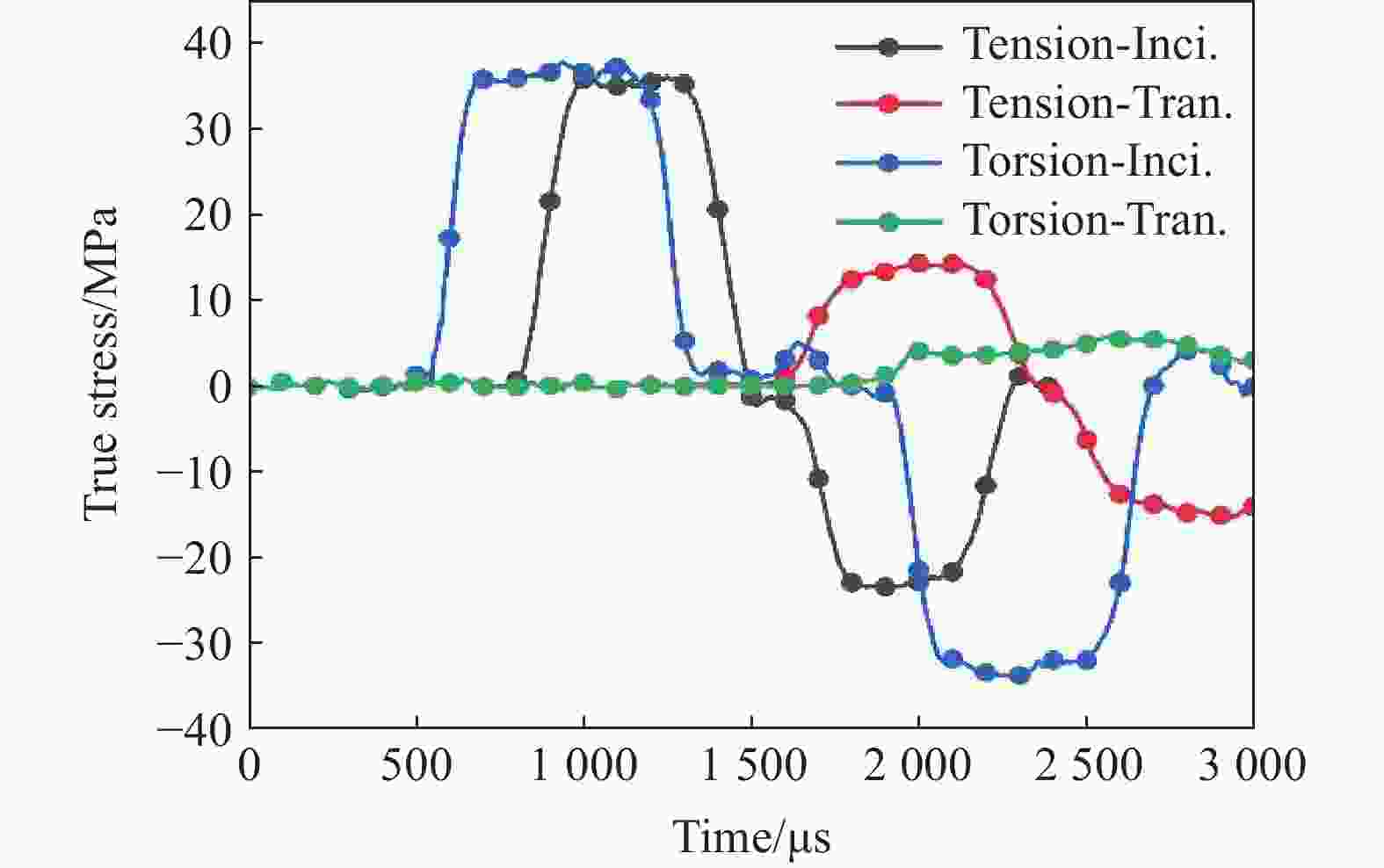
School of Aeronautics, Northwestern Polytechnical University, Xi'an 710072, Shaanxi, China

摘要

摘要: 为解决材料动态复合加载过程中实现稳定应力比的难题，基于电磁Hopkinson杆（electromagnetic Hopkinson bar, ESHB）平台开发了一种新型装置，实现了单边同步动态拉/压-扭复合加载。阐述了装置的构型与加载原理，该装置可以独立产生梯形拉伸/压缩应力波和扭转应力波。通过精度达0.1 μs的数字延时发生器确保了加载的同步性，可将不同类型波到达试样的时间差控制在5 μs内，克服了波速不同带来的挑战。此外，还分析了同步控制方法及波的传播历程。为验证该装置，对CoCrFeMnNi高熵合金试样进行了动态拉-扭实验。实验结果证明了该装置的高可靠性和有效性，加载过程中可以实现试样达到约1.7的稳定应力比。更重要的是，实验证明梯形波加载能显著提升动态复合加载中的应力比稳定性，效果远超正弦波加载。该实验方法使研究材料在复杂应力状态（高应变率、多轴加载）下的动态力学响应成为可能，稳定应力比加载的成功实现，为精准表征动态多轴条件下材料的屈服准则与失效机制开辟了新途径。
- 电磁Hopkinson杆 /
- 动态加载 /
- 多轴加载 /
- 恒定应力比
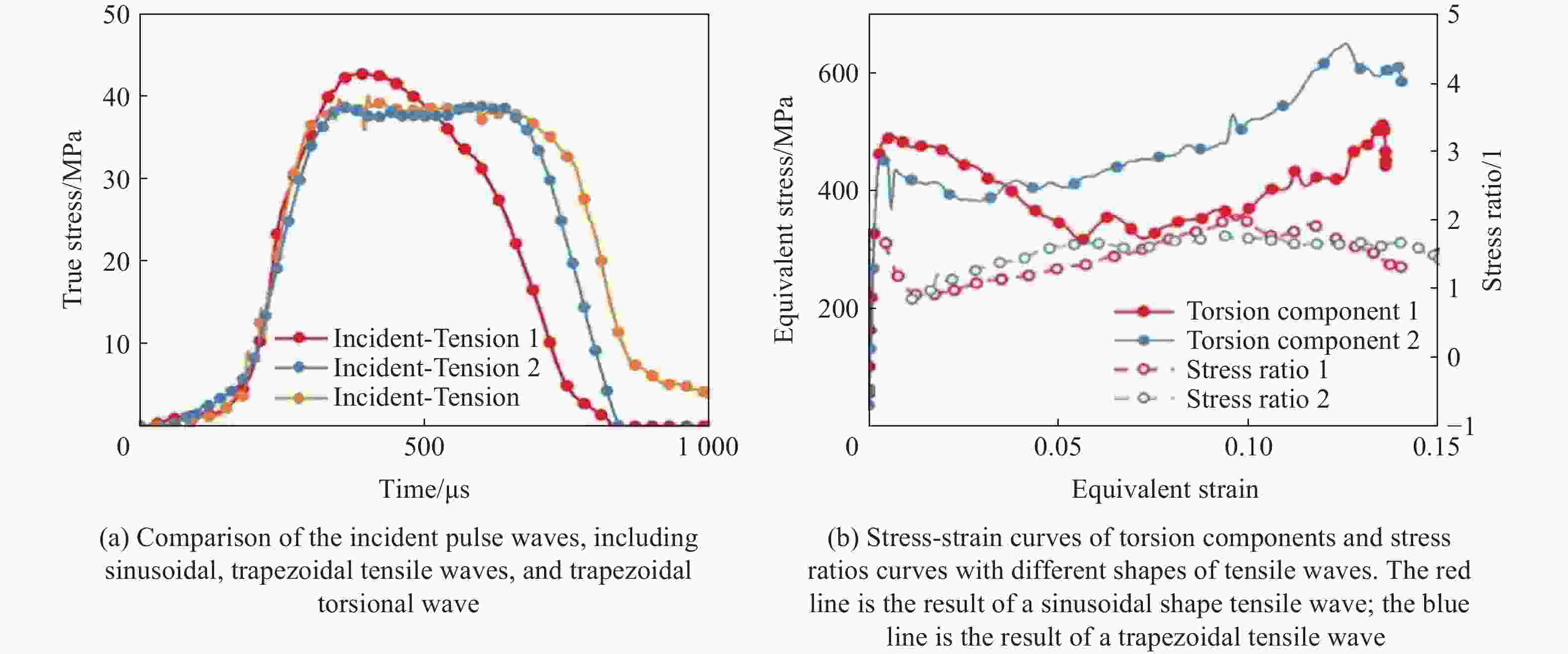
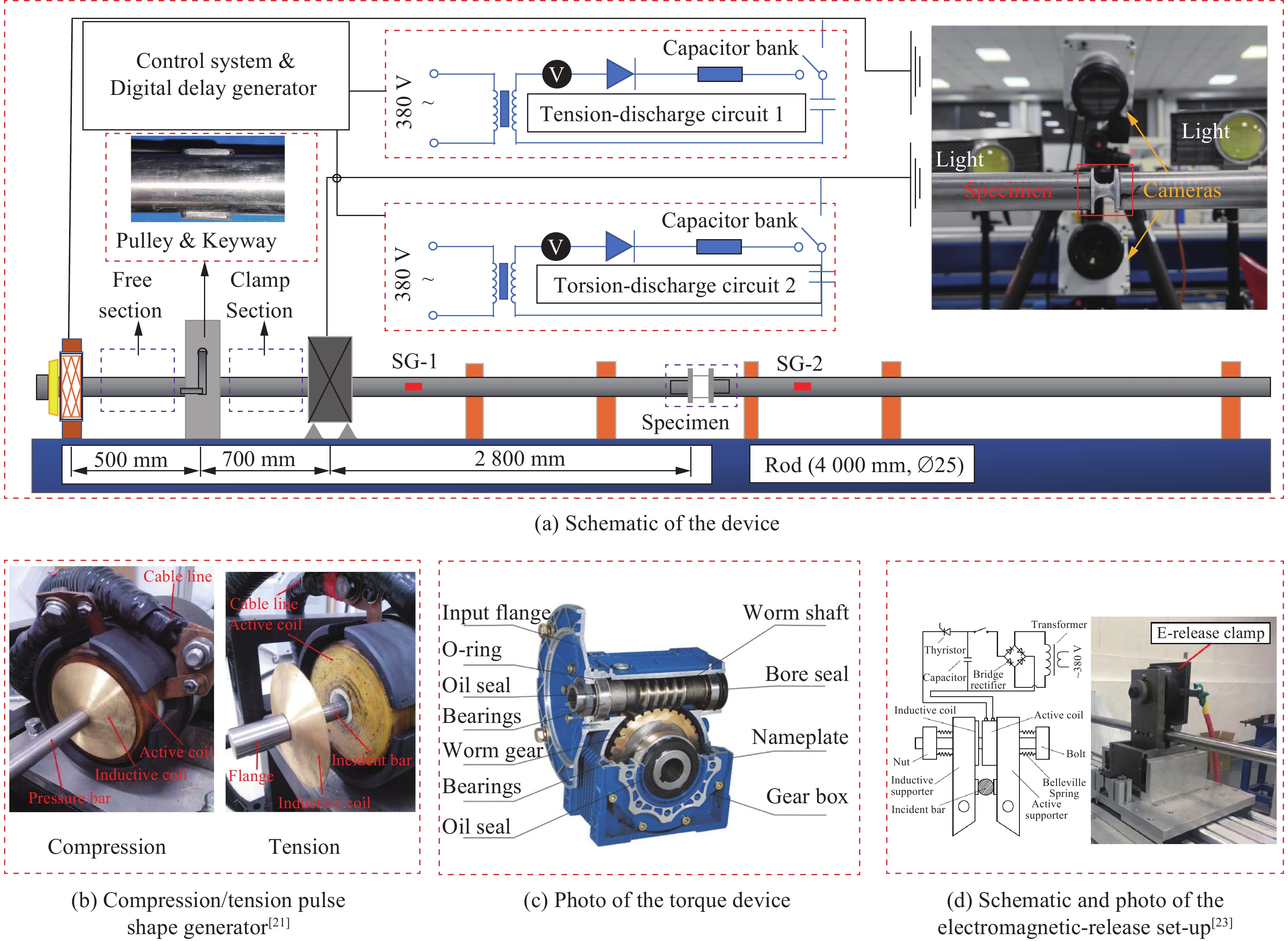
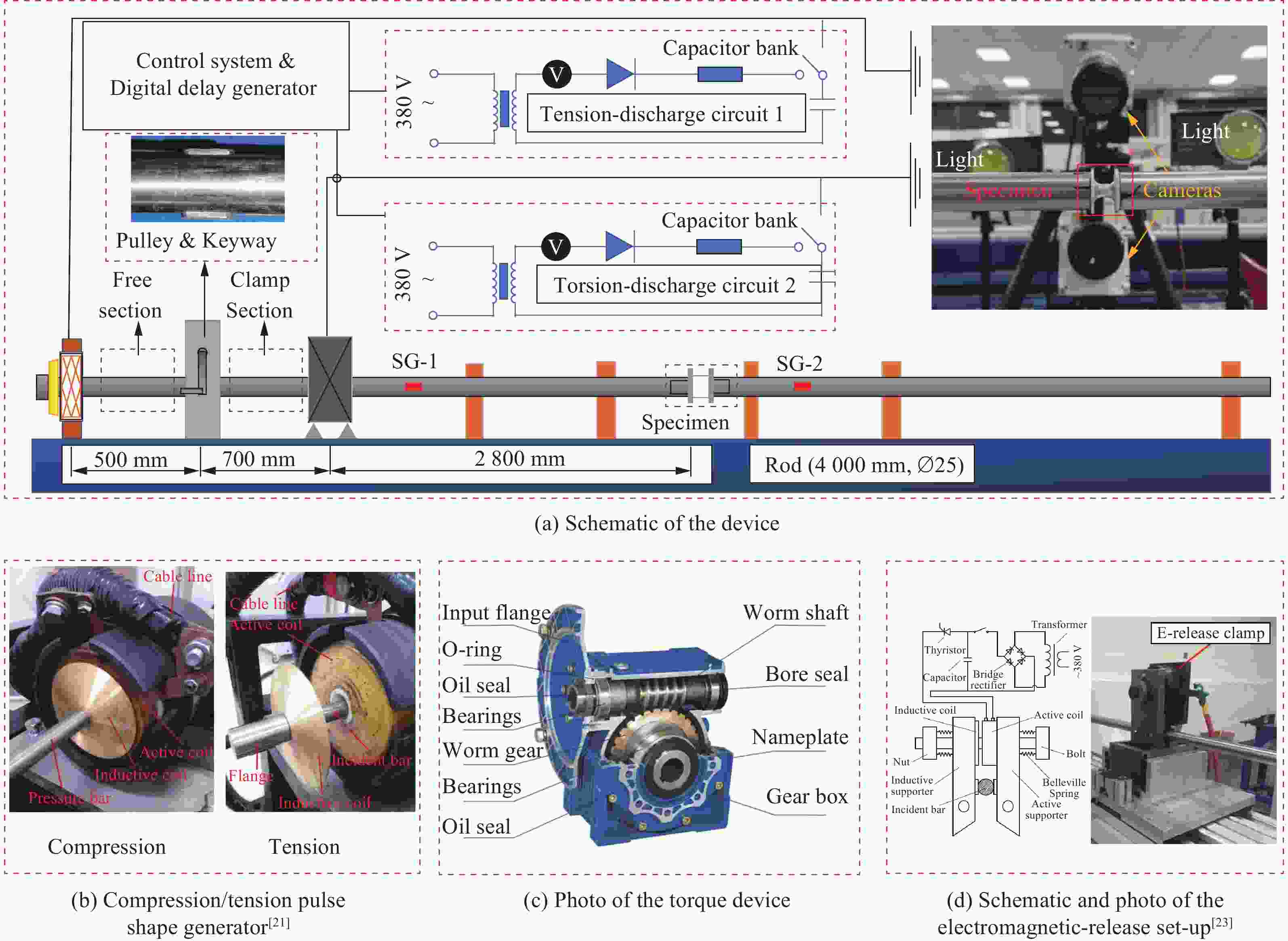
Abstract: In the field of material dynamic mechanical properties research, it is significant to obtain reliable data of materials under complex stress states. To address the challenge of achieving a stable stress ratio during combined loading, this work developed a novel device based on the electromagnetic Hopkinson bar (ESHB) platform. This device uniquely enables unilateral synchronous tension/compression-torsion combined dynamic loading. The paper detailed the device’s configuration and loading principles. The core innovation of this device is the independent generation of trapezoidal tensile/compressive and torsional stress waves. A multi-circuit pulse shaper produced tensile/compressive waves, while shear waves were generated using an electromagnetic clamp with torque storage. Crucially, a high-precision digital delay generator (DDG) ensured wave synchronization. With triggering accuracy within 0.1 μs, it controlled the arrival time difference of these distinct waves at the specimen to within 5 μs. This overcame the challenge posed by their different propagation velocities. Additionally, it described the synchronization control methodology and the wave propagation analysis essential for timing calculations. To validate the apparatus, dynamic tension-torsion experiments were conducted on CoCrFeMnNi high-entropy alloy specimens. The results show that the device is highly reliable and effective. It successfully achieved a stable stress ratio of approximately 1.7 throughout the loading duration. Furthermore, the experiments conclusively showed a key finding. Trapezoidal wave loading significantly enhances stress-ratio stability during combined dynamic loading. This improvement contrasts with the effect of traditional sinusoidal wave loading. This advancement offers a robust and controllable experimental method. It enables the study of materials’ dynamic mechanical responses under complex stress states. These states involve high-strain rates and multiaxial loading. This capability is especially valuable for aerospace, impact engineering, and materials science applications. The successful implementation of constant stress-ratio loading opens avenues for more accurate characterization of material yield criteria and failure mechanisms under dynamic multiaxial conditions.
- electromagnetic Hopkinson bar /
- dynamic loading /
- multiaxial loading /
- constant stress-ratio

HTML全文

图 1 电磁霍普金森拉/压-扭杆

Figure 1. Electromagnetic Hopkinson tension/compression-torsion bar (ESHT/C-T_orB).

下载: 全尺寸图片幻灯片

图 2 电路同步方法示意图

Figure 2. Schematic diagram of the synchronized method in T-Tor SHB

下载: 全尺寸图片幻灯片

图 3 拉伸/压缩波和扭转波的波传播时间-历程关系图

Figure 3. Time-distance diagram of wave propagation for both tensile/compressive stress wave and torsional stress wave

下载: 全尺寸图片幻灯片

图 4 试样的几何尺寸和实物图(单位：mm)

Figure 4. Geometry and photo of the specimens (unit: mm)

下载: 全尺寸图片幻灯片

图 5 动态同步拉伸-扭转联合加载的典型信号

Figure 5. Typical signals of combined dynamic tension-torsion loading

下载: 全尺寸图片幻灯片

图 6 不同加载条件下加载波的时间-应力曲线

Figure 6. Stress-time curves of loading wave with respect to different loading conditions

下载: 全尺寸图片幻灯片

图 7 动态同步拉伸-扭转联合加载的应力平衡性分析

Figure 7. Stress equilibrium analysis of combined dynamic tension-torsion loading

下载: 全尺寸图片幻灯片

图 8 应力比$ C=1.7 $时的典型拉伸-扭转实验结果

Figure 8. Typical tension-torsion experimental results with the stress ratio of 1.7

下载: 全尺寸图片幻灯片

图 9 典型动态拉伸-扭转实验的入射波

Figure 9. Typical tension-torsion incident pulse waves

下载: 全尺寸图片幻灯片

图 10 不同形状拉伸波作用下实验结果的对比

Figure 10. Comparison of experimental results under tensile waves with different shapes

下载: 全尺寸图片幻灯片

表 1 高熵合金组分

Table 1. Chemical compositions of the HEAs

元素摩尔比/%

Cr 19.91$ \pm $0.11
Mn 20.07$ \pm $0.13
Fe 19.91$ \pm $0.13
Co 20.29$ \pm $0.15
Ni 19.81$ \pm $0.15

下载: 导出CSV

参考文献(29)

[1]	周伦, 苏兴亚, 敬霖, 等. 6061-T6铝合金动态拉伸本构关系及失效行为 [J]. 爆炸与冲击, 2022, 42(9): 091407. DOI: 10.11883/bzycj-2022-0154. ZHOU L, SU X Y, JING L, et al. Dynamic tensile constitutive relationship and failure behavior of 6061-T6 aluminum alloy [J]. Explosion and Shock Waves, 2022, 42(9): 091407. DOI: 10.11883/bzycj-2022-0154.
[2]	周刚毅, 董新龙, 付应乾, 等. 不同加载状态下TA2钛合金绝热剪切破坏响应特性 [J]. 力学学报, 2016, 48(6): 1353–1361. DOI: 10.6052/0459-1879-16-198. ZHOU G Y, DONG X L, FU Y Q, et al. An experimental study on adiabatic shear behavior of TA2 titanium alloy subject to different loading condition [J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(6): 1353–1361. DOI: 10.6052/0459-1879-16-198.
[3]	李海峰, 门建兵, 金文, 等. Ta-Hf-Nb-Zr体系高熵合金J-C模型及应用试验 [J]. 爆炸与冲击, 2025, 45(3): 033103. DOI: 10.11883/bzycj-2024-0069. LI H F, MEN J B, JIN W, et al. J-C model of high-entropy alloy Ta-Hf-Nb-Zr system and its application test [J]. Explosion and Shock Waves, 2025, 45(3): 033103. DOI: 10.11883/bzycj-2024-0069.
[4]	MIYAMBO M E, VON KALLON D V, PANDELANI T, et al. Review of the development of the split Hopkinson pressure bar [J]. Procedia CIRP, 2023, 119: 800–808. DOI: 10.1016/j.procir.2023.04.010.
[5]	KOLSKY H. An investigation of the mechanical properties of materials at very high rates of loading [J]. Proceedings of the Physical Society. Section B, 1949, 62(11): 676–700. DOI: 10.1088/0370-1301/62/11/302.
[6]	胡时胜, 王礼立, 宋力, 等. Hopkinson压杆技术在中国的发展回顾 [J]. 爆炸与冲击, 2014, 34(6): 641–657. DOI: 10.11883/1001-1455(2014)06-0641-17. HU S S, WANG L L, SONG L, et al. Review of the development of Hopkinson pressure bar technique in China [J]. Explosion and Shock Waves, 2014, 34(6): 641–657. DOI: 10.11883/1001-1455(2014)06-0641-17.
[7]	YIN J P, MIAO Y G, WU Z B, et al. A novel Hopkinson tension bar system for testing polymers under intermediate strain rate and large deformation [J]. International Journal of Impact Engineering, 2025, 198: 105197. DOI: 10.1016/j.ijimpeng.2024.105197.
[8]	MIAO Y G, DU B, MA C B, et al. Some fundamental problems concerning the measurement accuracy of the Hopkinson tension bar technique [J]. Measurement Science and Technology, 2019, 30(5): 055009. DOI: 10.1088/1361-6501/ab01b5.
[9]	NEMAT-NASSER S, ISAACS J B, STARRETT J E. Hopkinson techniques for dynamic recovery experiments [J]. Proceedings of the Royal Society of London. Series A: Mathematical and Physical Sciences, 1991, 435(1894): 371–391. DOI: 10.1098/rspa.1991.0150.
[10]	王维斌, 索涛, 郭亚洲, 等. 电磁霍普金森杆实验技术及研究进展 [J]. 力学进展, 2021, 51(4): 729–754. DOI: 10.6052/1000-0992-20-024. WANG W B, SUO T, GUO Y Z, et al. Experimental technique and research progress of electromagnetic Hopkinson bar [J]. Advances in Mechanics, 2021, 51(4): 729–754. DOI: 10.6052/1000-0992-20-024.
[11]	杜冰, 郭亚洲, 李玉龙. 一种基于电磁霍普金森杆的材料动态包辛格效应测试装置及方法 [J]. 爆炸与冲击, 2020, 40(8): 081101. DOI: 10.11883/bzycj-2020-0050. DU B, GUO Y Z, LI Y L. A novel technique for determining the dynamic Bauschinger effect by electromagnetic Hopkinson bar [J]. Explosion and Shock Waves, 2020, 40(8): 081101. DOI: 10.11883/bzycj-2020-0050.
[12]	许泽建, 丁晓燕, 张炜琪, 等. 一种用于材料高应变率剪切性能测试的新型加载技术 [J]. 力学学报, 2016, 48(3): 654–659. DOI: 10.6052/0459-1879-15-445. XU Z J, DING X Y, ZHANG W Q, et al. A new loading technique for measuring shearing properties of materials under high strain rates [J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(3): 654–659. DOI: 10.6052/0459-1879-15-445.
[13]	CAMPBELL J D, DOWLING A R. The behaviour of materials subjected to dynamic incremental shear loading [J]. Journal of the Mechanics and Physics of Solids, 1970, 18(1): 43–63. DOI: 10.1016/0022-5096(70)90013-X.
[14]	BAKER W E, YEW C H. Strain-rate effects in the propagation of torsional plastic waves [J]. Journal of Applied Mechanics, 1966, 33(4): 917–923. DOI: 10.1115/1.3625202.
[15]	NICHOLAS T, LAWSON J E. On the determination of the mechanical properties of materials at high shear-strain rates [J]. Journal of the Mechanics and Physics of Solids, 1972, 20(2): 57–62. DOI: 10.1016/0022-5096(72)90030-0.
[16]	ELEICHE A M, CAMPBELL J D. Strain-rate effects during reverse torsional shear [J]. Experimental Mechanics, 1976, 16(8): 281–290. DOI: 10.1007/bf02324016.
[17]	NIE X, PRABHU R, CHEN W W, et al. A Kolsky torsion bar technique for characterization of dynamic shear response of soft materials [J]. Experimental Mechanics, 2011, 51(9): 1527–1534. DOI: 10.1007/s11340-011-9481-4.
[18]	CLAUS B J, NIE X, MARTIN B E, et al. A side-impact torsion Kolsky bar: development of interfaces and a pulse-shaping technique [J]. Experimental Mechanics, 2015, 55(7): 1367–1374. DOI: 10.1007/s11340-015-0032-2.
[19]	HUANG H, FENG R. A study of the dynamic tribological response of closed fracture surface pairs by Kolsky-bar compression-shear experiment [J]. International Journal of Solids and Structures, 2004, 41(11/12): 2821–2835. DOI: 10.1016/j.ijsolstr.2004.01.005.
[20]	郭伟国, 李玉龙, 索涛. 应力波基础简明教程 [M]. 西安: 西北工业大学出版社, 2007.
[21]	NIE H L, SUO T, WU B B, et al. A versatile split Hopkinson pressure bar using electromagnetic loading [J]. International Journal of Impact Engineering, 2018, 116: 94–104. DOI: 10.1016/j.ijimpeng.2018.02.002.
[22]	NIE H L, SUO T, SHI X P, et al. Symmetric split Hopkinson compression and tension tests using synchronized electromagnetic stress pulse generators [J]. International Journal of Impact Engineering, 2018, 122: 73–82. DOI: 10.1016/j.ijimpeng.2018.08.004.
[23]	LIU C L, WANG W B, SUO T, et al. Achieving combined tension-torsion Split Hopkinson Bar test based on electromagnetic loading [J]. International Journal of Impact Engineering, 2022, 168: 104287. DOI: 10.1016/j.ijimpeng.2022.104287.
[24]	LIU C L, YANG X, DING Y, et al. The yielding behavior of TU00 pure copper under impact loading [J]. International Journal of Mechanical Sciences, 2023, 245: 108110. DOI: 10.1016/j.ijmecsci.2023.108110.
[25]	WANG W B, WANG J B, DU B, et al. The achievement of constant strain rates in electromagnetic Hopkinson bar test [J]. International Journal of Impact Engineering, 2025, 195: 105121. DOI: 10.1016/j.ijimpeng.2024.105121.
[26]	束德林. 工程材料力学性能 [M]. 2版. 北京: 机械工业出版社, 2007.
[27]	DU B, DING Y, BAI X, et al. Tensile behavior of CoCrFeMnNi high-entropy alloy with intermediate strain rate included [J]. European Journal of Mechanics - A/Solids, 2024, 108: 105412. DOI: 10.1016/j.euromechsol.2024.105412.
[28]	YANG X, LIU C L, DING Y, et al. Dynamic yielding and plastic flow behavior of Ti-6Al-4V under complex loading [J]. International Journal of Solids and Structures, 2023, 283: 112476. DOI: 10.1016/j.ijsolstr.2023.112476.
[29]	余同希, 薛璞. 工程塑性力学 [M]. 2版. 北京: 高等教育出版社, 2010.