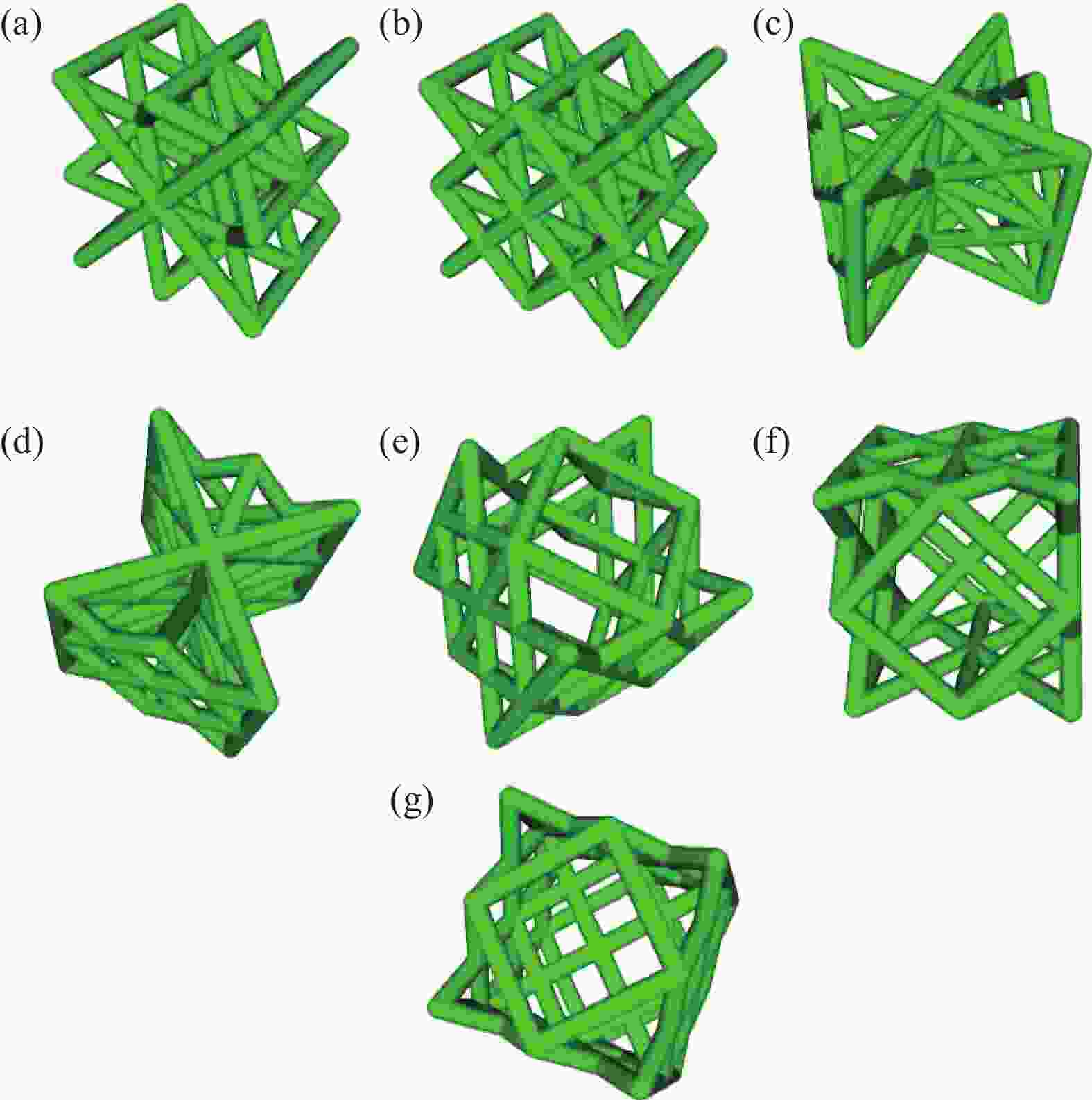
Data-driven multi-objective optimization for lattice-based metamaterials
-
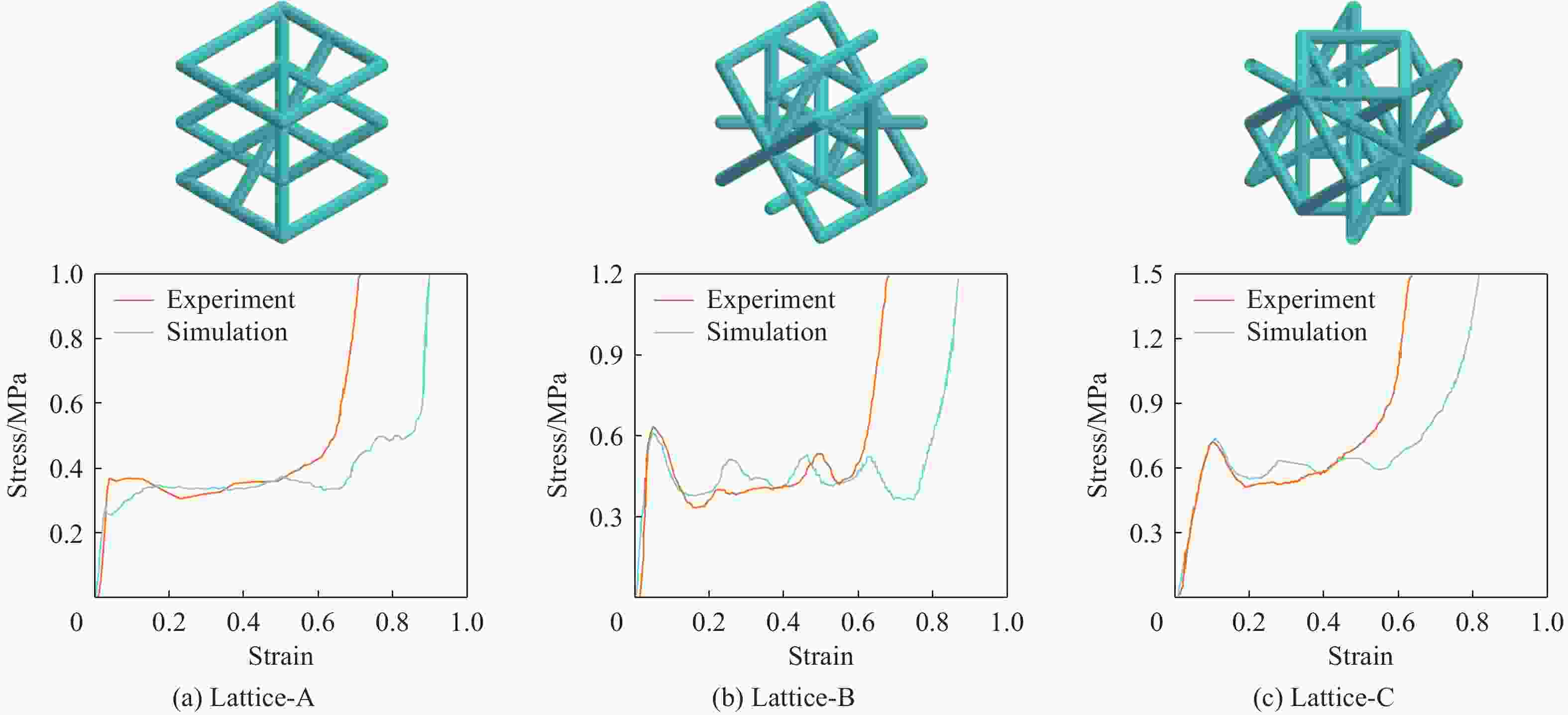
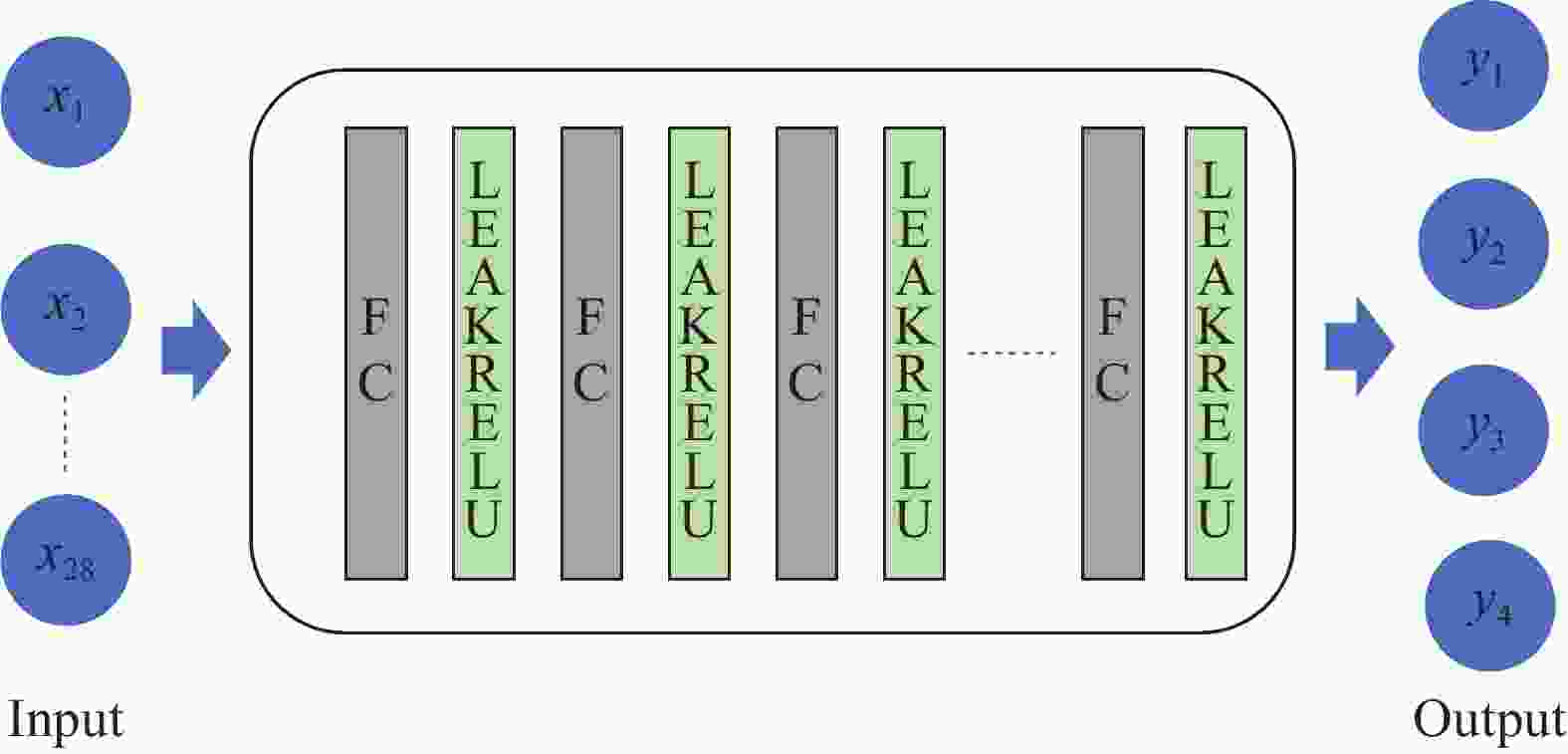
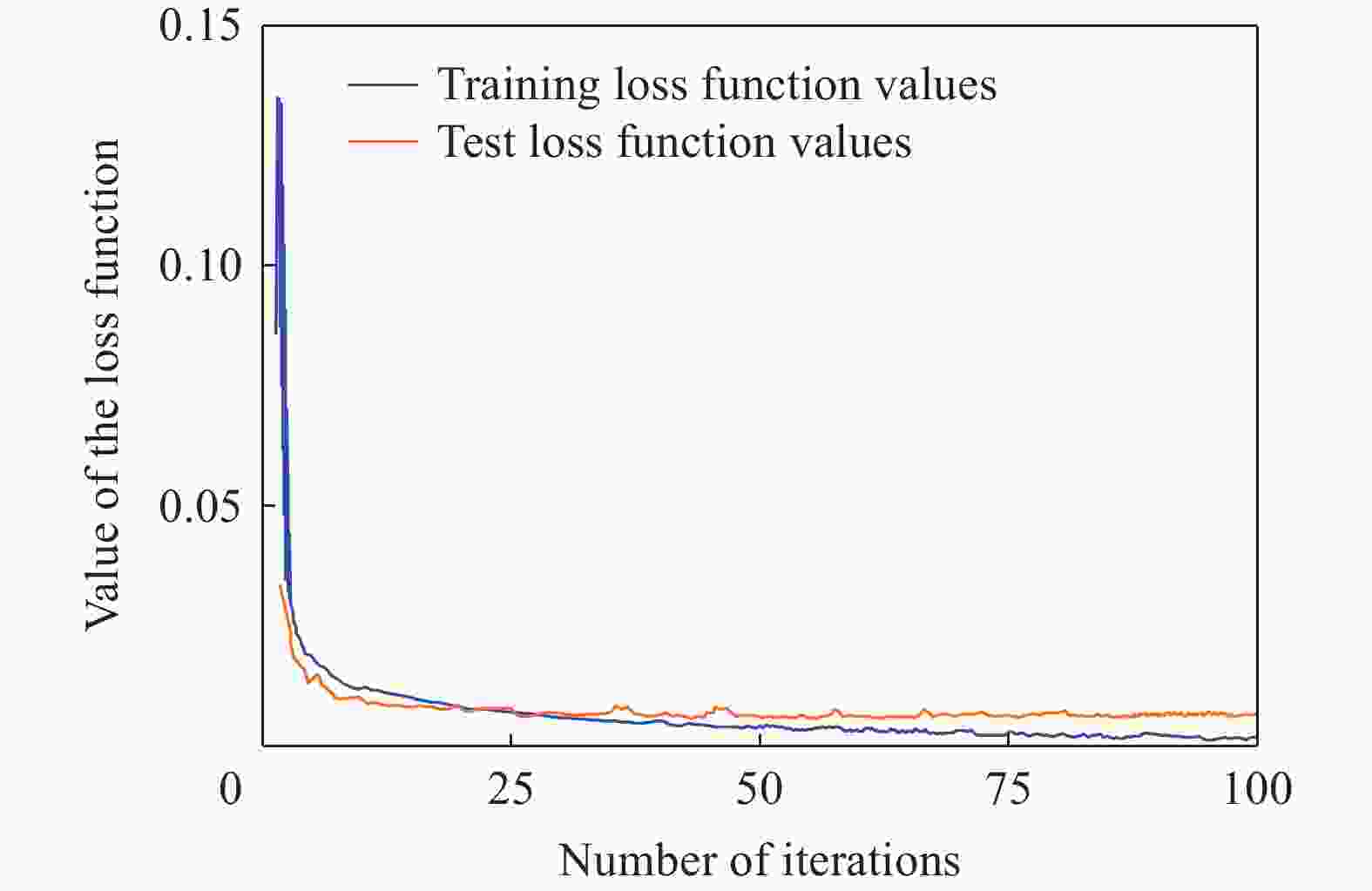
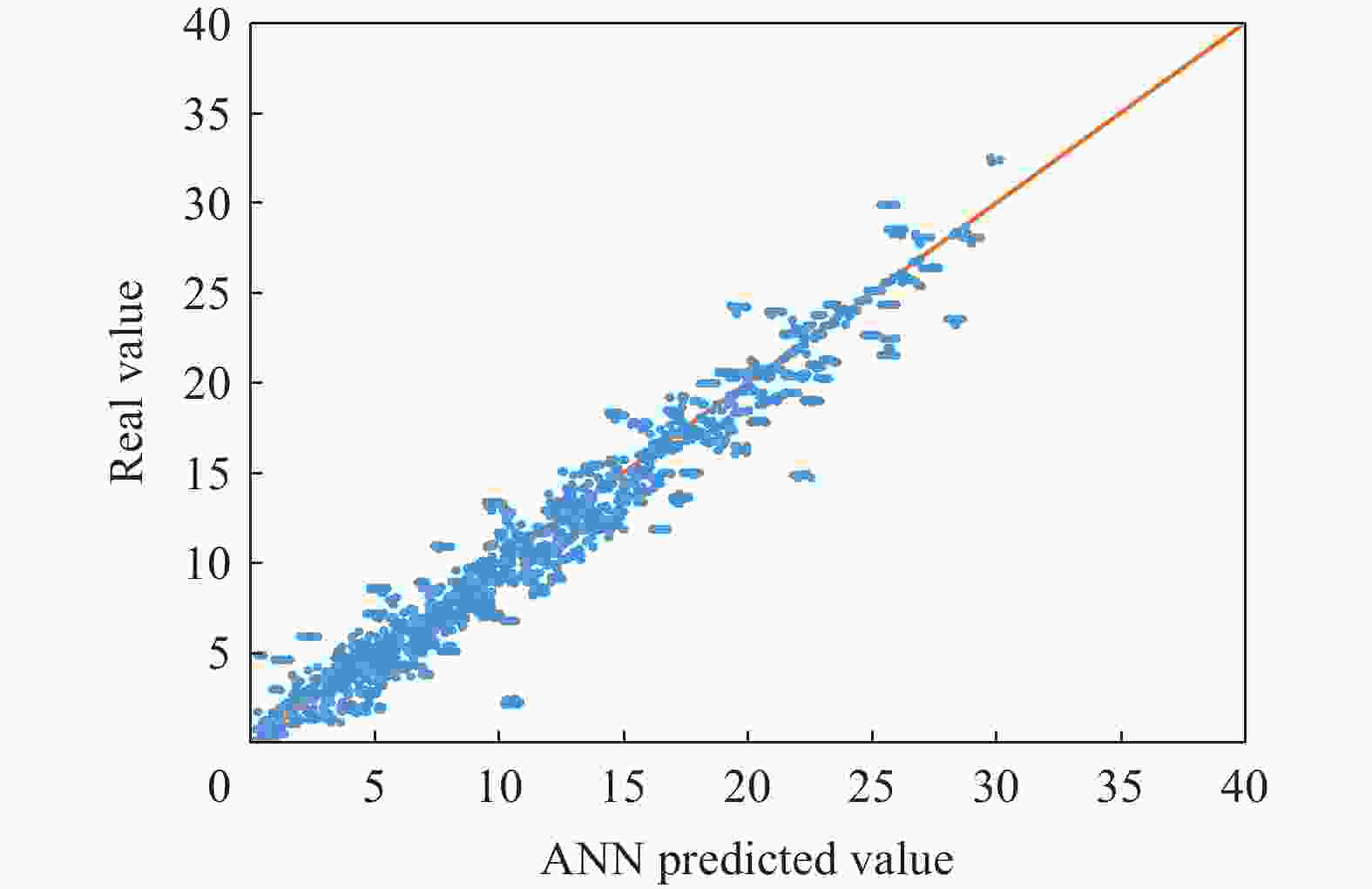
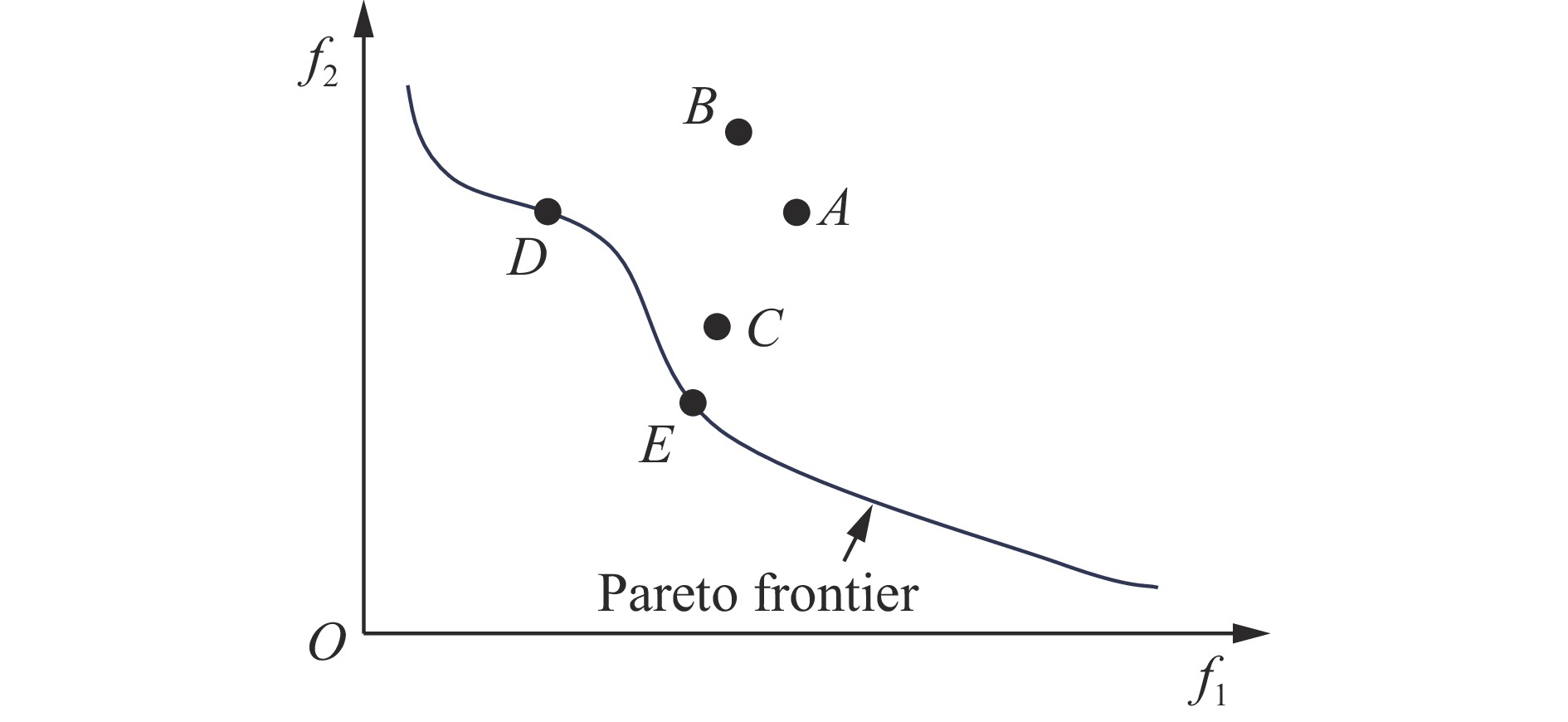
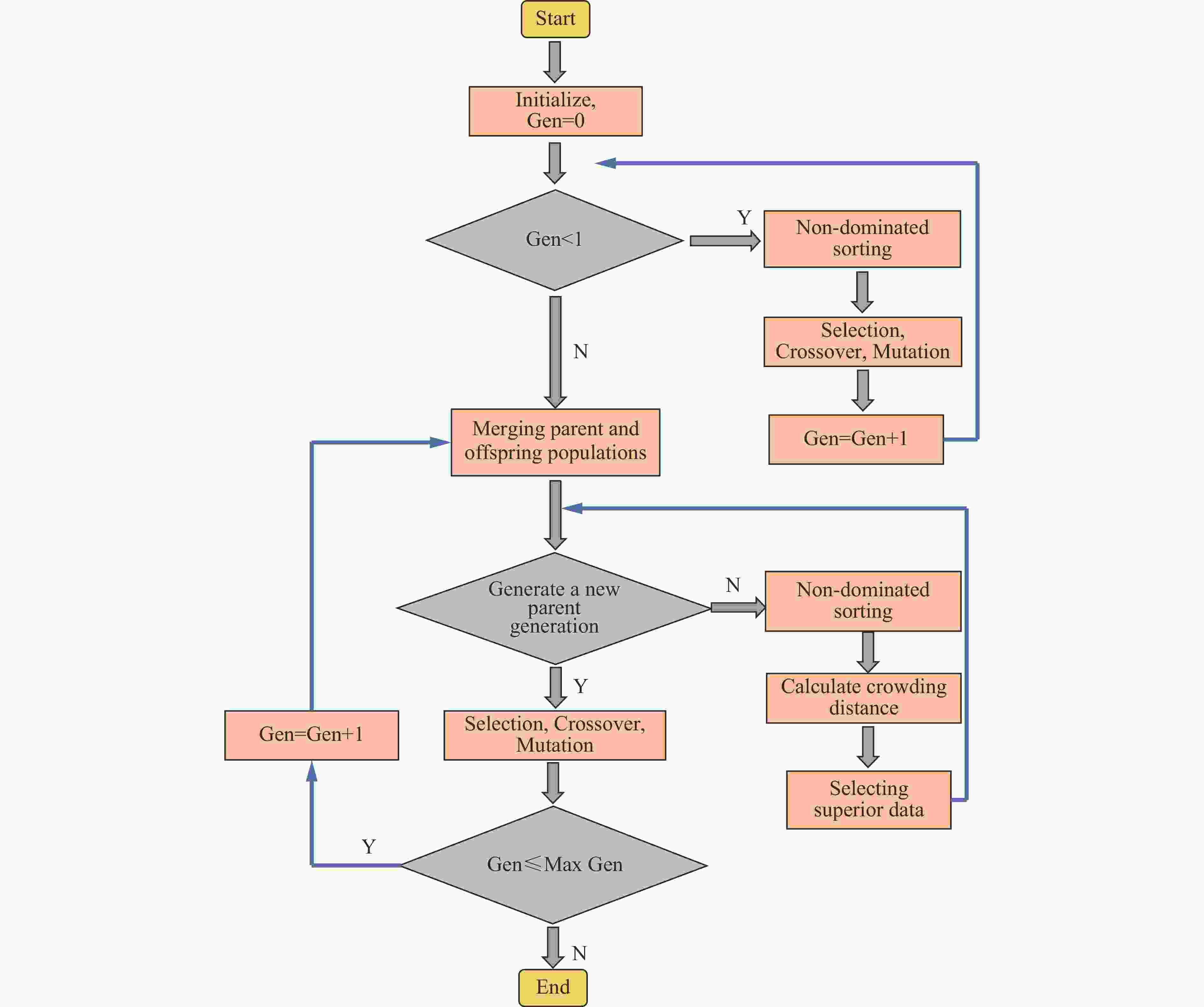
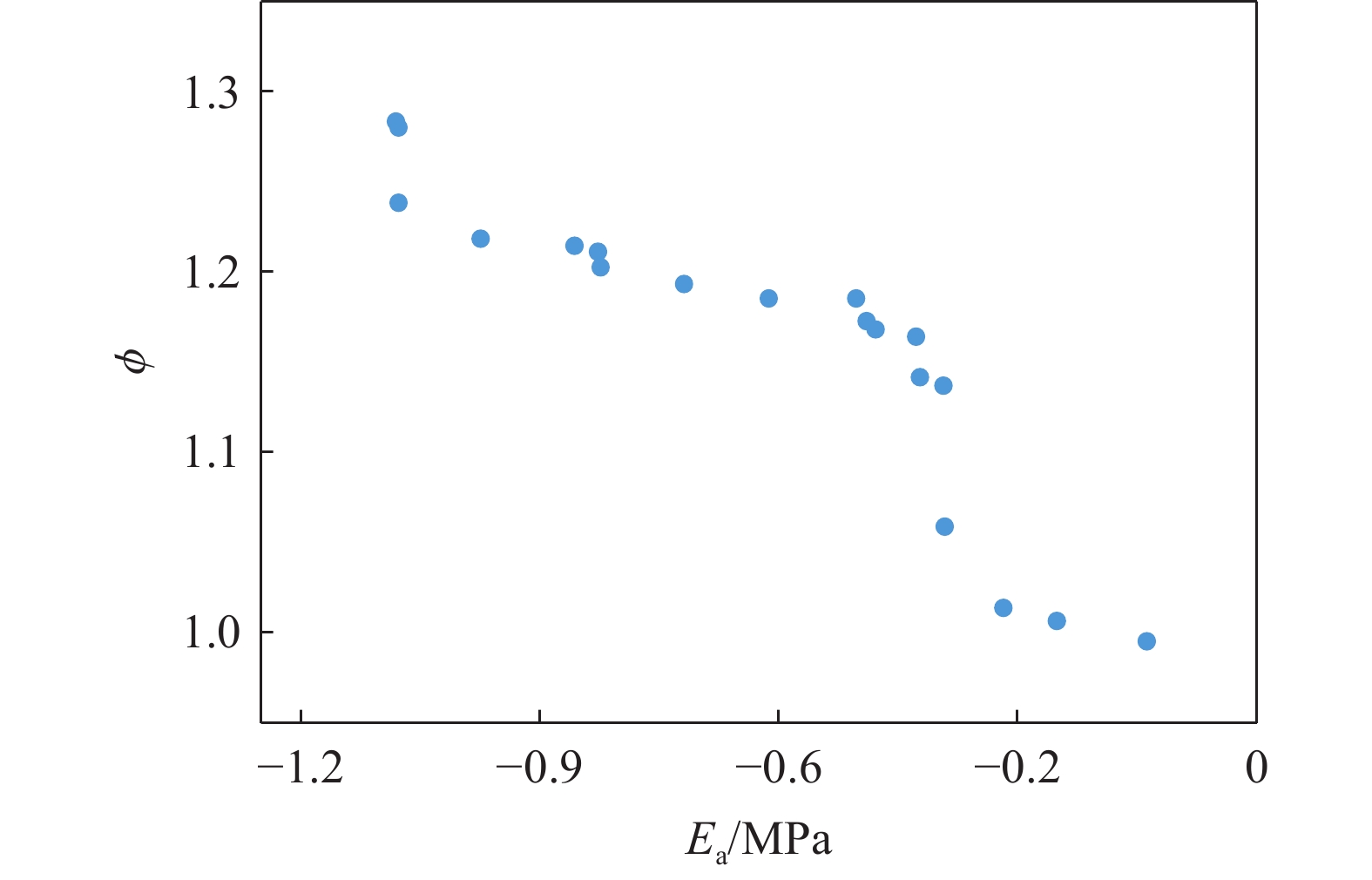
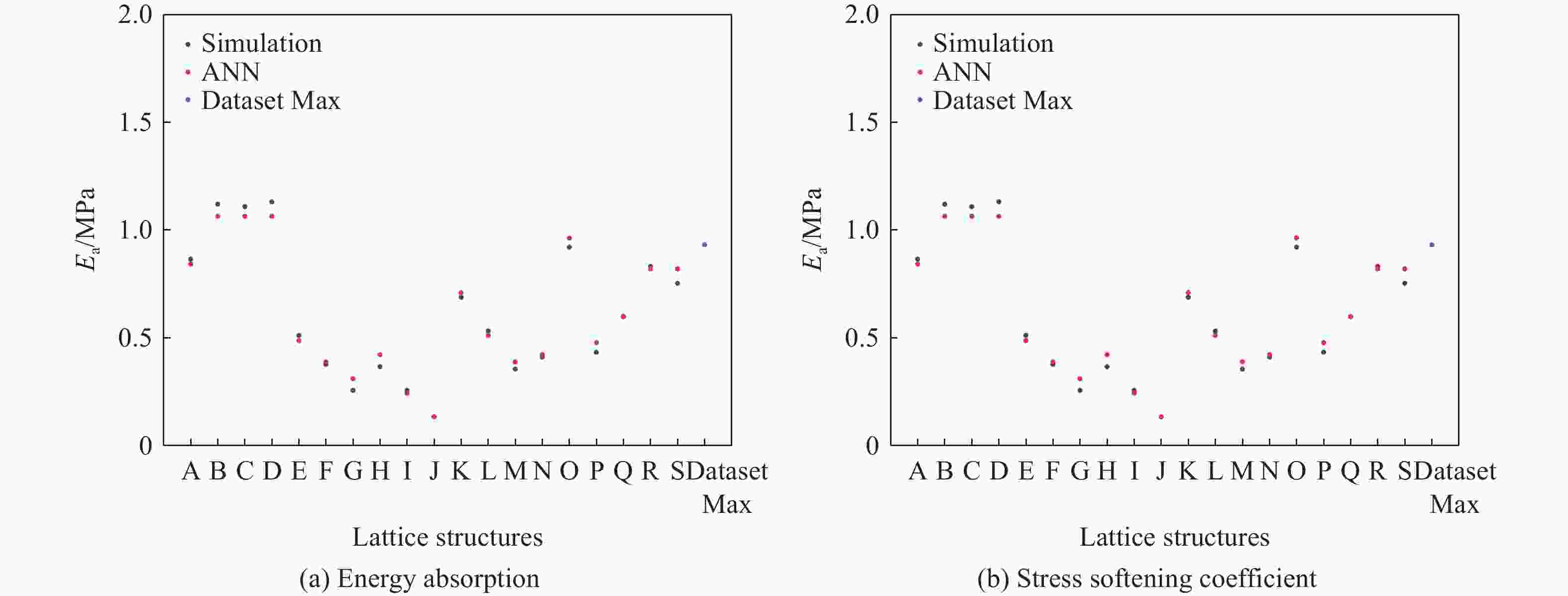
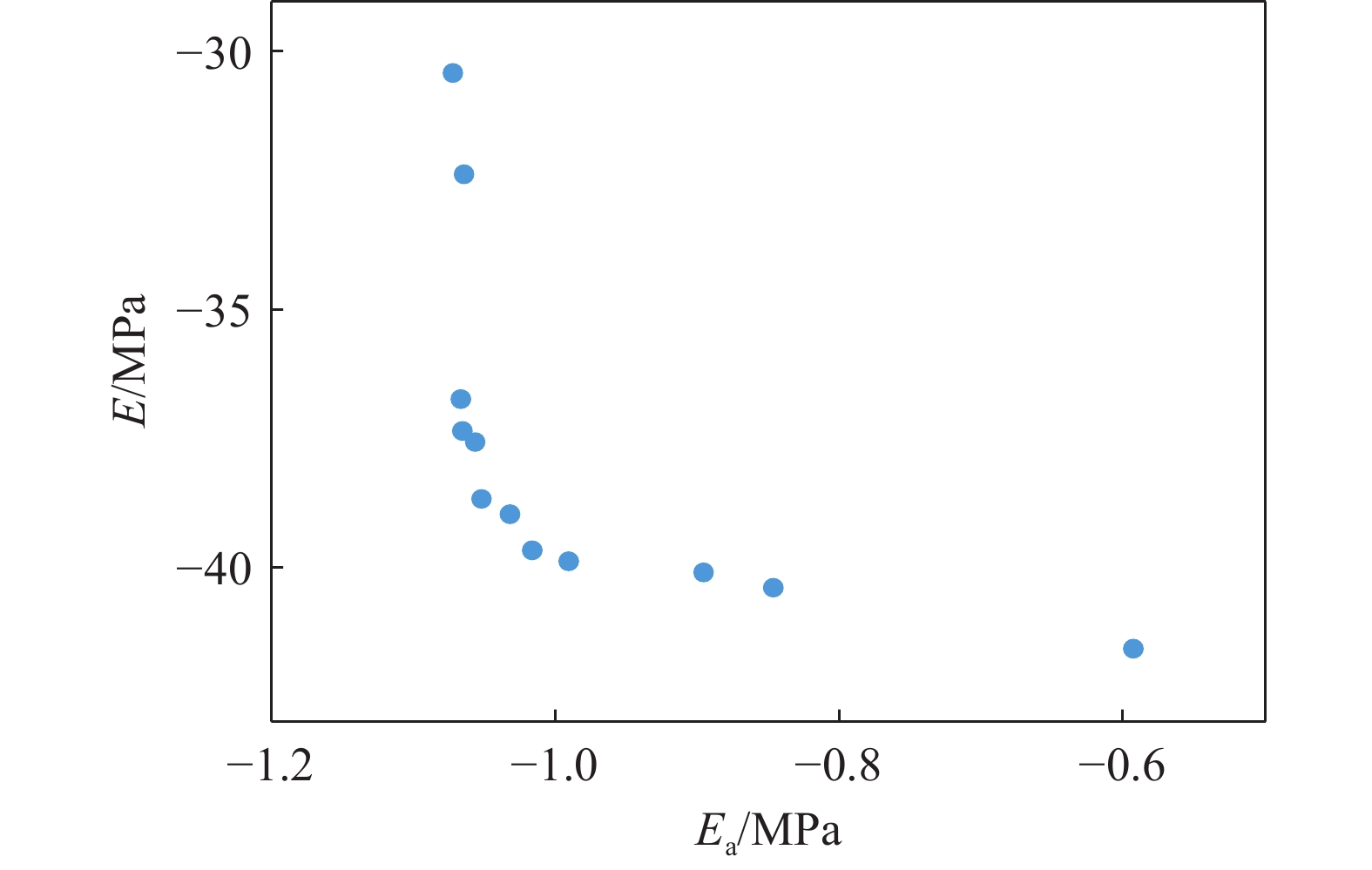
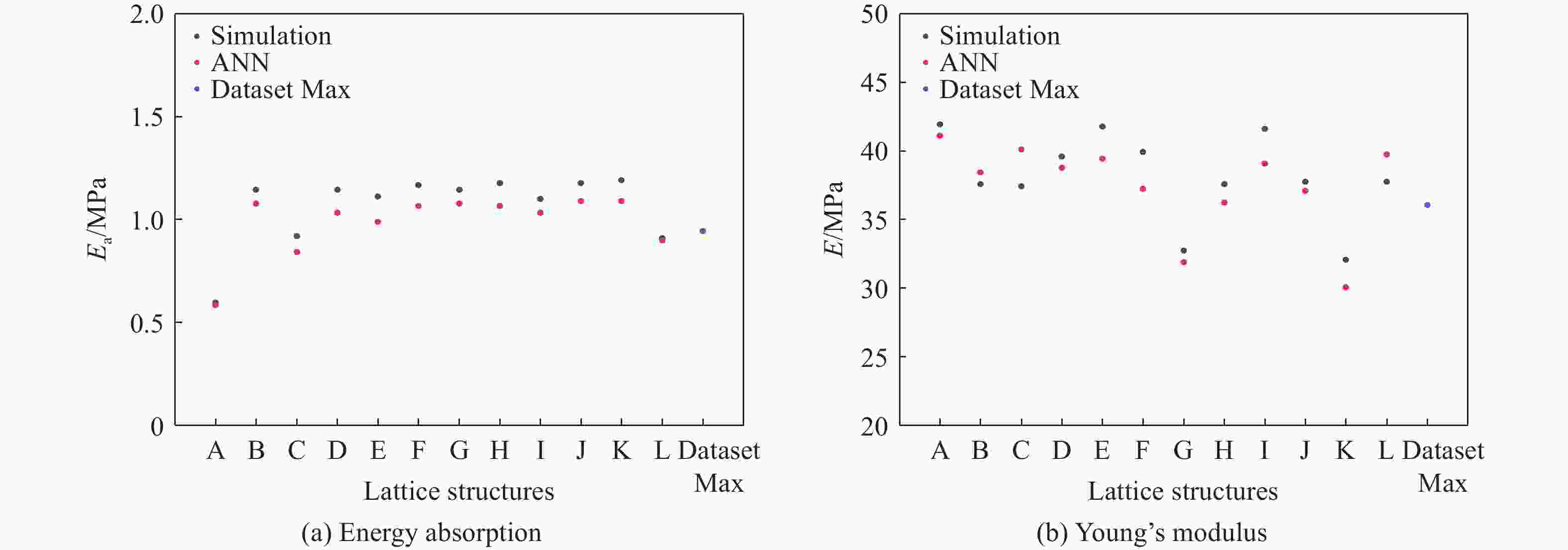
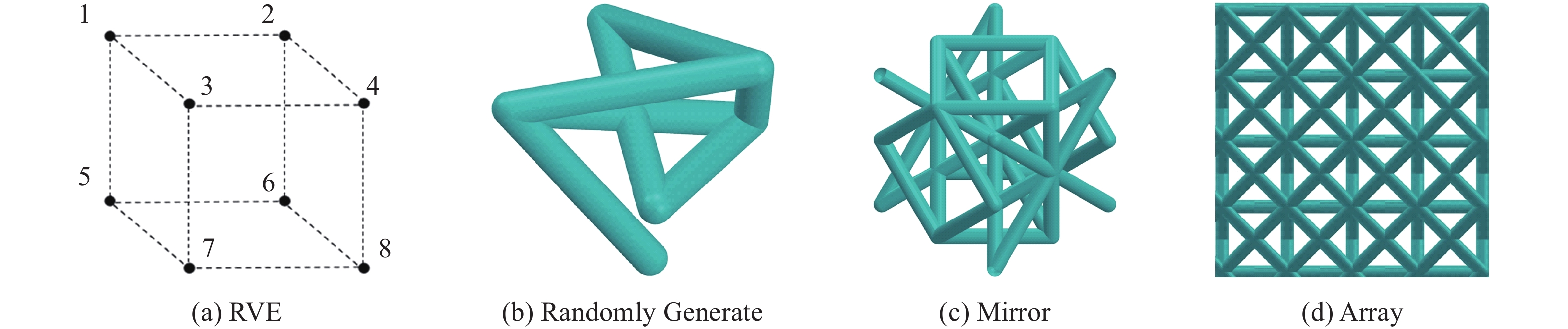
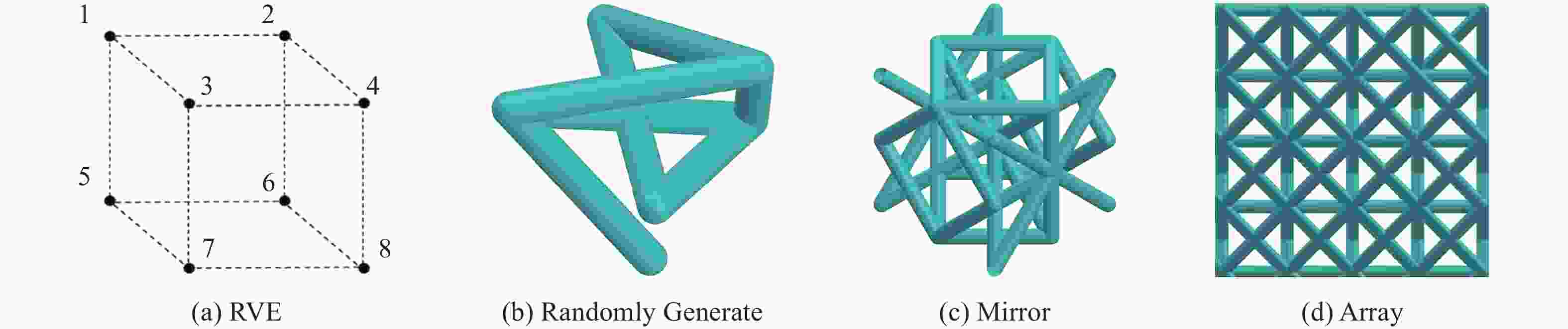
摘要: 桁架类点阵超材料是一类超轻质承载吸能材料，在冲击防护领域具有广阔的应用前景。然而，由于点阵超材料细观构型参数空间庞大，且构型参数与力学响应之间存在复杂的非线性关系，其性能优化面临巨大挑战。针对上述问题，基于桁架类点阵超材料的细观结构特征，提出了一种高效的快速数字化建模方法，并利用 Python 脚本驱动 Abaqus 仿真软件，实现了材料的批量化建模与仿真分析。在此基础上，通过有限元数值模拟建立了不同构型点阵超材料的准静态压缩性能数据集，并利用实验验证了数据集的可靠性。随后，训练了一个人工神经网络（artificial neural network，ANN）模型作为代理函数，并将其嵌入非支配排序遗传算法（non-dominated sorting genetic algorithm II，NSGA-II），对点阵超材料开展多目标优化设计，获得了具有高承载能力、高吸能特性以及兼顾承载吸能性能的点阵超材料构型。研究结果表明，融合机器学习技术与有限元仿真，可有效降低优化设计的计算成本，为复杂点阵超材料的快速性能优化与定制化设计提供技术支撑。Abstract: Strut-based lattice metamaterials are a category of ultra-lightweight, load-bearing, and energy-absorbing materials with broad application prospects in fields such as impact protection, aerospace engineering, and lightweight structural design. Benefiting from their unique periodic architectures and adjustable meso-structural parameters, these materials exhibit exceptional mechanical tunability and multifunctional potential. However, due to the extensive parameter space of mesoscopic configurations and the highly nonlinear correlation between the structural geometry and the mechanical response, the optimization of mechanical performance for lattice metamaterials remains a formidable challenge. Based on the meso-structural characteristics of strut-based lattice metamaterials, an efficient rapid digital modeling method was proposed. A Python script coupled with Abaqus software was utilized for the rapid modeling of truss lattice metamaterials and fast calculations about the mechanical properties of the metamaterials. Based on the calculation results, a machine learning dataset was constructed. Three types of truss lattice structures were randomly selected and additively manufactured. Quasi-static compression tests on these three lattice structures were conducted using a universal testing machine to verify the reliability of the dataset. Subsequently, an artificial neural network (ANN) was trained to rapidly predict the mechanical properties of the truss lattice metamaterials. Focusing on the load-bearing capacity, energy absorption capability, and the concurrent optimization of both, a non-dominated sorting genetic algorithm II (NSGA-Ⅱ) was employed. The well-trained ANN served as a surrogate model embedded within NSGA-II. Lattice configurations that exhibited high load-bearing capacity and superior energy absorption characteristics were generated by the optimization process. These configurations also achieved a balance between load-bearing and energy-absorption performance, facilitating the optimization design of truss lattice metamaterials. Additionally, simulation validations confirmed the reliability of the optimization outcomes, demonstrating the effectiveness of integrating ANN with evolutionary algorithms for the advanced design of metamaterials. By integrating machine learning with numerical simulations, the computational cost of optimization design was effectively reduced, offering support for the rapid performance optimization and customized design of complex lattice metamaterials.
-
图 4 实验所得曲线和模拟所得曲线的对比
Figure 4. Comparison between the experimental curves and the simulated curves
图 5 实验变形模式和数值模拟变形模式的对比
Figure 5. Comparison between the experimental deformation mode and the numerical simulation deformation mode
图 8 ANN预测值与真实值之间的线性关系
Figure 8. Linear relationship between ANN predicted values and true values
图 11 承载型点阵超材料优化设计的Pareto前沿
Figure 11. Pareto front for optimization design of load-bearing lattice-based metamaterials
图 12 承载型点阵超材料的优化胞元构型
Figure 12. Optimized unit cell configurations of load-bearing lattice-based metamaterials
图 13 承载型点阵超材料优化设计的模拟验证结果
Figure 13. Simulation verification results for optimization design of load-bearing lattice-based metamaterials
图 14 吸能型点阵超材料优化设计的Pareto前沿
Figure 14. Pareto front for optimization design of energy-absorbing lattice-based metamaterials
图 15 吸能型点阵超材料的优化胞元构型
Figure 15. Optimized unit cell configurations of energy-absorbing lattice-based metamaterials
图 16 吸能型点阵超材料优化设计的仿真验证结果
Figure 16. Simulation verification results for optimization design of energy-absorbing lattice-based metamaterials
图 17 兼顾承载吸能点阵超材料优化设计的Pareto前沿
Figure 17. Pareto front for optimization design of lattice-based metamaterials with both high energy absorption and load bearing capacity
图 18 兼顾承载吸能点阵超材料的优化胞元构型
Figure 18. Optimized unit cell configurations of lattice-based metamaterials with both high energy absorption and load bearing capacity
图 19 兼顾承载吸能点阵超材料优化设计的仿真验证结果
Figure 19. Simulation verification results for optimization design of lattice-based metamaterials with both high energy absorption and load-bearing capacities
图 20 Lattice-(e)的实验与模拟力学响应对比
Figure 20. Comparison between experimental and simulated mechanical responses of Lattice-(e)
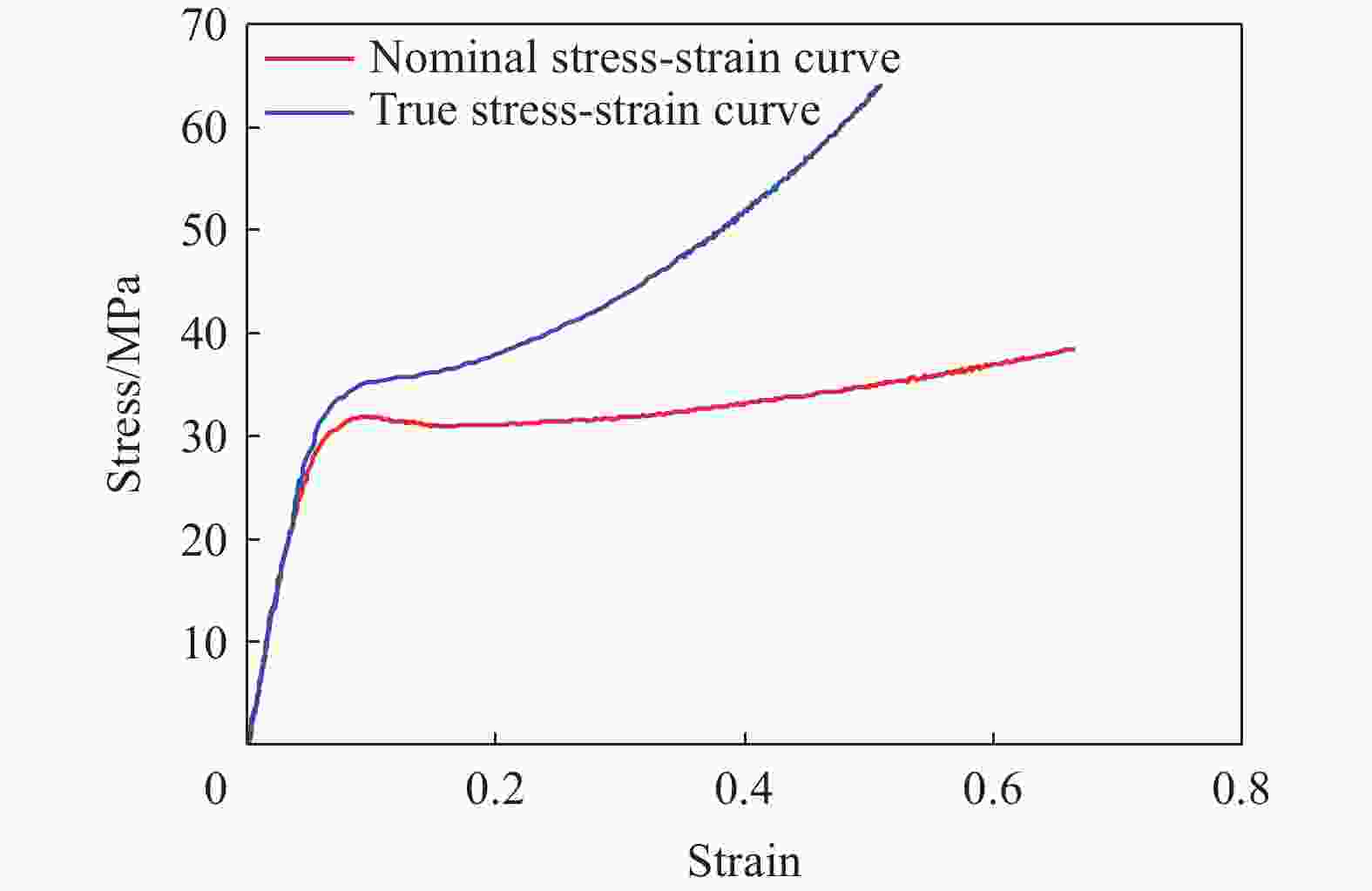
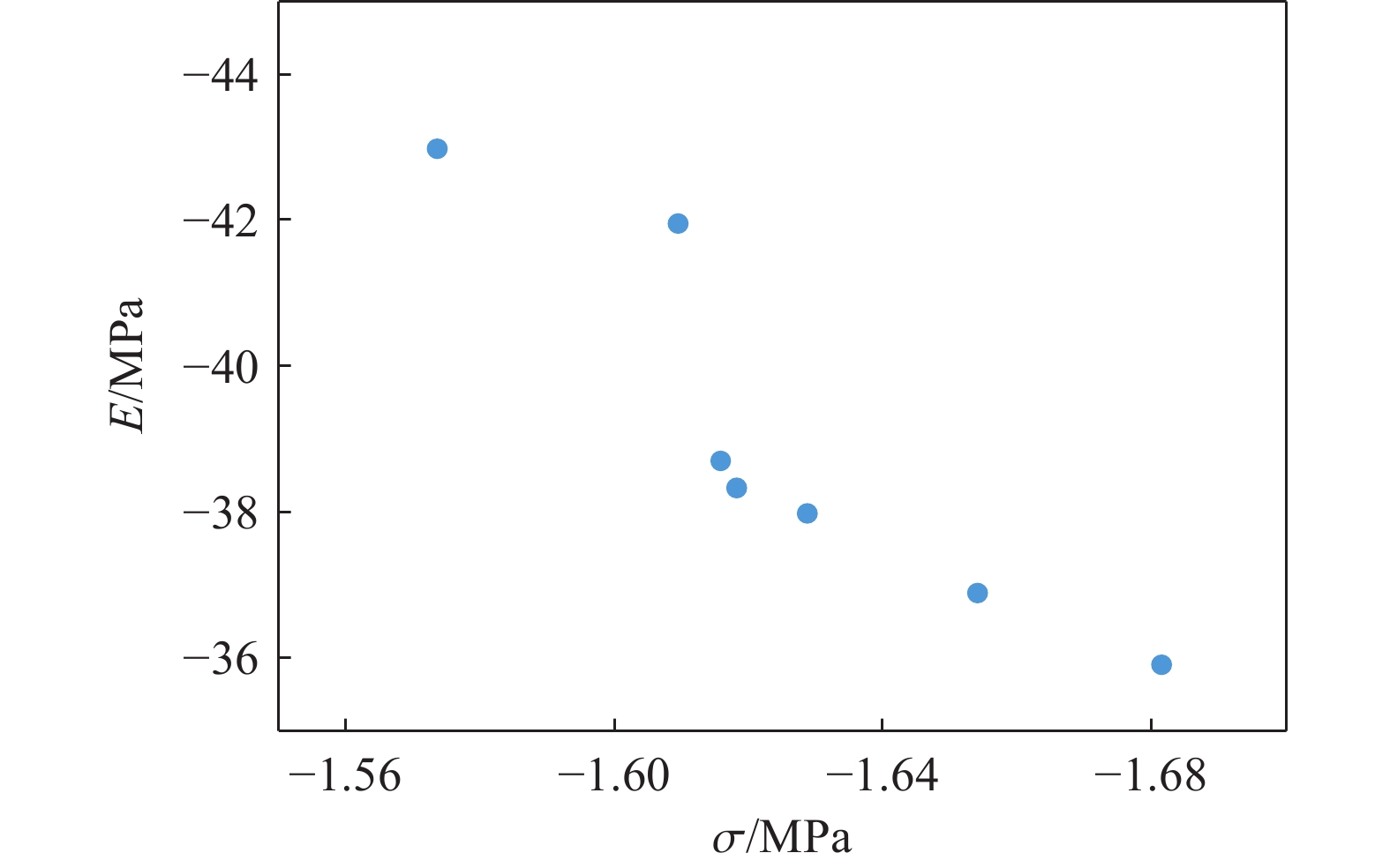
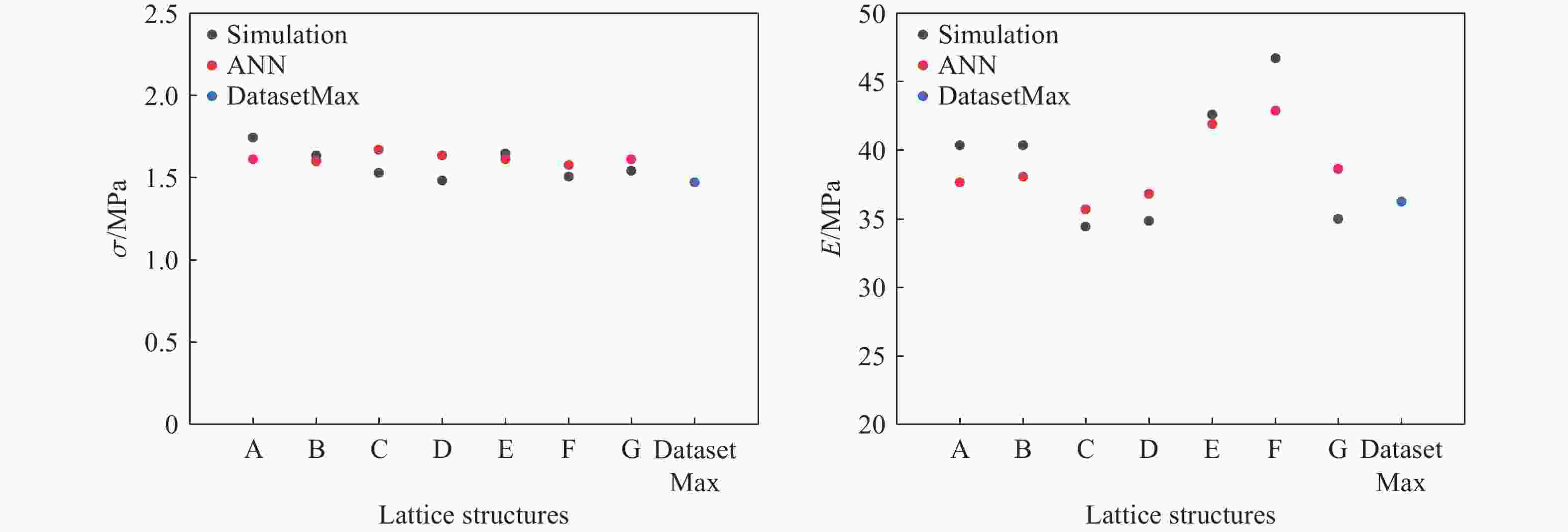
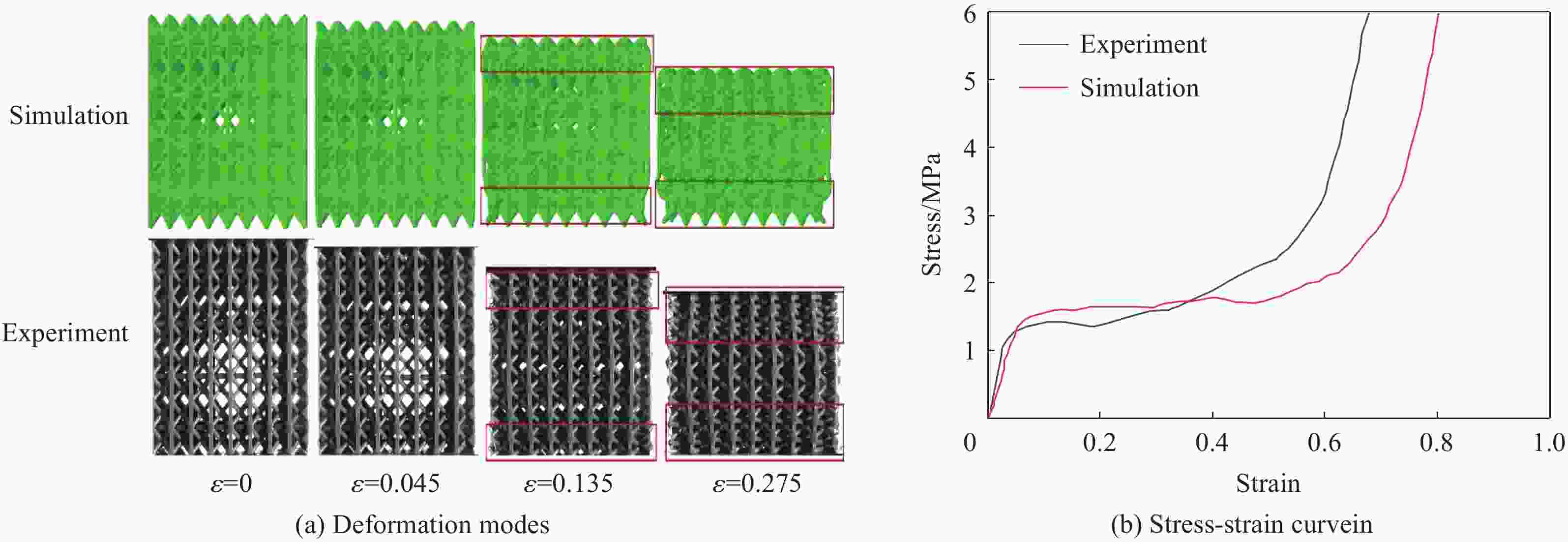
表 1 结构(e)的实验和模拟结果对比
Table 1. Comparison of experimental and simulation results of Lattice-(e)
方法 弹性模量/MPa 吸能密度/MPa 仿真 42.2244 1.1029 实验 43.4396 1.2082 相对误差/% 2.8 8.7 
下载: 导出CSV
-
[1] CHOUGRANI L, PERNOT J P, VÉRON P, et al. Lattice structure lightweight triangulation for additive manufacturing [J]. Computer-Aided Design, 2017, 90: 95–104. DOI: 10.1016/j.cad.2017.05.016. [2] YIN S, GUO W H, WANG H T, et al. Strong and tough bioinspired additive-manufactured dual-phase mechanical metamaterial composites [J]. Journal of the Mechanics and Physics of Solids, 2021, 149: 104341. DOI: 10.1016/j.jmps.2021.104341. [3] PORTELA C M, GREER J R, KOCHMANN D M. Impact of node geometry on the effective stiffness of non-slender three-dimensional truss lattice architectures [J]. Extreme Mechanics Letters, 2018, 22: 138–148. DOI: 10.1016/j.eml.2018.06.004. [4] LING C, CERNICCHI A, GILCHRIST M D, et al. Mechanical behaviour of additively-manufactured polymeric octet-truss lattice structures under quasi-static and dynamic compressive loading [J]. Materials & Design, 2019, 162: 106–118. DOI: 10.1016/j.matdes.2018.11.035. [5] YIN H F, ZHANG W Z, ZHU L C, et al. Review on lattice structures for energy absorption properties [J]. Composite Structures, 2023, 304(Pt 1): 116397. DOI: 10.1016/j.compstruct.2022.116397. [6] NAZIR A, ABATE K M, KUMAR A, et al. A state-of-the-art review on types, design, optimization, and additive manufacturing of cellular structures [J]. The International Journal of Advanced Manufacturing Technology, 2019, 104(9-12): 3489–3510. DOI: 10.1007/s00170-019-04085-3. [7] HU L L, ZHOU M Z, DENG H. Dynamic crushing response of auxetic honeycombs under large deformation: theoretical analysis and numerical simulation [J]. Thin-Walled Structures, 2018, 131: 373–384. DOI: 10.1016/j.tws.2018.04.020. [8] ZHANG D H, FEI Q G, LIU J Z, et al. Crushing of vertex-based hierarchical honeycombs with triangular substructures [J]. Thin-Walled Structures, 2020, 146: 106436. DOI: 10.1016/j.tws.2019.106436. [9] NEČEMER B, GLODEŽ S, NOVAK N, et al. Numerical modelling of a chiral auxetic cellular structure under multiaxial loading conditions [J]. Theoretical and Applied Fracture Mechanics, 2020, 107: 102514. DOI: 10.1016/j.tafmec.2020.102514. [10] ANDREW J J, SCHNEIDER J, UBAID J, et al. Energy absorption characteristics of additively manufactured plate-lattices under low- velocity impact loading [J]. International Journal of Impact Engineering, 2021, 149: 103768. DOI: 10.1016/j.ijimpeng.2020.103768. [11] MIRALBES R, RANZ D, PASCUAL F J, et al. Characterization of additively manufactured triply periodic minimal surface structures under compressive loading [J]. Mechanics of Advanced Materials and Structures, 2022, 29(13): 1841–1855. DOI: 10.1080/15376494.2020.1842948. [12] MA Q P, YAN Z J, ZHANG L, et al. The family of elastically isotropic stretching-dominated cubic truss lattices [J]. International Journal of Solids and Structures, 2022, 239/240: 111451. DOI: 10.1016/j.ijsolstr.2022.111451. [13] MACONACHIE T, LEARY M, LOZANOVSKI B, et al. SLM lattice structures: properties, performance, applications and challenges [J]. Materials & Design, 2019, 183: 108137. DOI: 10.1016/j.matdes.2019.108137. [14] MORA S, PUGNO N M, MISSERONI D. 3D printed architected lattice structures by material jetting [J]. Materials Today, 2022, 59: 107–132. DOI: 10.1016/j.mattod.2022.05.008. [15] TANCOGNE-DEJEAN T, SPIERINGS A B, MOHR D. Additively-manufactured metallic micro-lattice materials for high specific energy absorption under static and dynamic loading [J]. Acta Materialia, 2016, 116: 14–28. DOI: 10.1016/j.actamat.2016.05.054. [16] EPASTO G, PALOMBA G, D'ANDREA D, et al. Ti-6Al-4V ELI microlattice structures manufactured by electron beam melting: effect of unit cell dimensions and morphology on mechanical behaviour [J]. Materials Science and Engineering: A, 2019, 753: 31–41. DOI: 10.1016/j.msea.2019.03.014. [17] WANG S H, MA Y B, DENG Z C, et al. Two elastically equivalent compound truss lattice materials with controllable anisotropic mechanical properties [J]. International Journal of Mechanical Sciences, 2022, 213: 106879. DOI: 10.1016/j.ijmecsci.2021.106879. [18] DONDA K, BRAHMKHATRI P, ZHU Y F, et al. Machine learning for inverse design of acoustic and elastic metamaterials [J]. Current Opinion in Solid State and Materials Science, 2025, 35: 101218. DOI: 10.1016/j.cossms.2025.101218. [19] XU W, LIU C, GUO Y L, et al. Problem-Independent Machine Learning (PIML) enhanced 3D lattice composite structures optimization via moving morphable components approach [J]. Composite Structures, 2025, 369: 119330. DOI: 10.1016/j.compstruct.2025.119330. [20] ZHAO S Y, ZHAO Z, YANG Z C, et al. Functionally graded graphene reinforced composite structures: a review [J]. Engineering Structures, 2020, 210: 110339. DOI: 10.1016/j.engstruct.2020.110339. [21] ZHANG X C, SONG Z Y, LI Y N, et al. Generative inverse design of metamaterials with customized stress-strain response [J]. International Journal of Mechanical Sciences, 2025, 306: 110875. DOI: 10.1016/j.ijmecsci.2025.110875. [22] SEPASDAR R, KARPATNE A, SHAKIBA M. A data-driven approach to full-field nonlinear stress distribution and failure pattern prediction in composites using deep learning [J]. Computer Methods in Applied Mechanics and Engineering, 2022, 397: 115126. DOI: 10.1016/j.cma.2022.115126. [23] PELOQUIN J, KIRILLOVA A, RUDIN C, et al. Prediction of tensile performance for 3D printed photopolymer gyroid lattices using structural porosity, base material properties, and machine learning [J]. Materials & Design, 2023, 232: 112126. DOI: 10.1016/j.matdes.2023.112126. [24] GLAESENER R N, KUMAR S, LESTRINGANT C, et al. Predicting the influence of geometric imperfections on the mechanical response of 2D and 3D periodic trusses [J]. Acta Materialia, 2023, 254: 118918. DOI: 10.1016/j.actamat.2023.118918. [25] YU G J, XIAO L J, SONG W D. Deep learning-based heterogeneous strategy for customizing responses of lattice structures [J]. International Journal of Mechanical Sciences, 2022, 229: 107531. DOI: 10.1016/j.ijmecsci.2022.107531. [26] SANTOSA S P, WIERZBICKI T, HANSSEN A G, et al. Experimental and numerical studies of foam-filled sections [J]. International Journal of Impact Engineering, 2000, 24(5): 509–534. DOI: 10.1016/S0734-743X(99)00036-6. [27] LE V T, DINH D M, TRAN V C, et al. Modelling, analysis, and multi-objective optimization of single weld bead characteristics in wire arc additive manufacturing of Inconel 625 based on machine learning and NSGA-II [J]. Materials Today Communications, 2025, 49: 113831. DOI: 10.1016/j.mtcomm.2025.113831. -
计量
- 文章访问数: 261
- HTML全文浏览量: 34
- PDF下载量: 107
- 被引次数: 0