Dynamic compression behavior of rock and simulation of damage effects of hypervelocity kinetic energy bomb
-
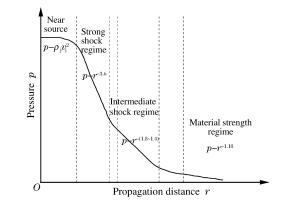
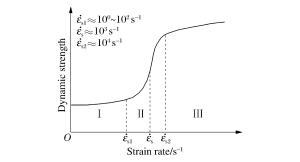
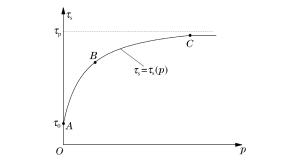
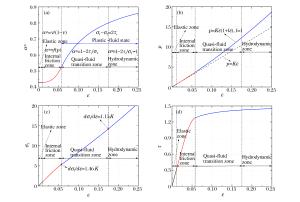
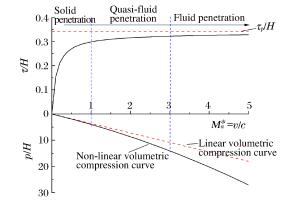
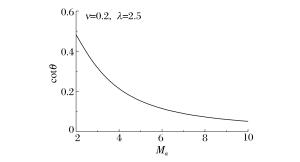
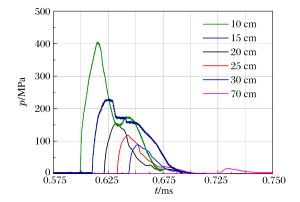
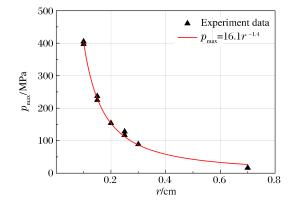
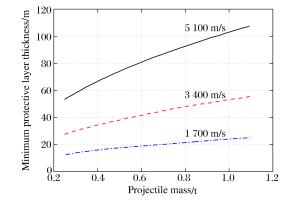
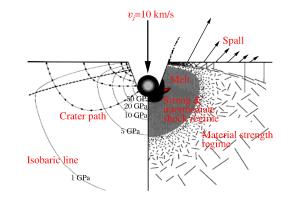
摘要: 目前正在研制的超高速动能武器对地打击速度达(5~15)马赫左右, 具有侵彻机理独特, 毁伤效应倍增的特点, 现有理论难以准确描述。本文系统总结了侵爆近区岩石介质的动态可压缩性行为, 发现(5~15)马赫超高速弹侵彻近区岩石介质介于流体和固体弹塑性之间的内摩擦侧限压力状态, 创新提出流体弹塑性内摩擦侵彻理论模型, 填补了低应力弹塑区到高应力流体区之间的应力状态表征空区, 首次获得随弹体侵速变化的弹靶相互作用全过程阻抗演变公式, 界定了钻地弹固体侵彻、拟流体侵彻和流体侵彻的最小动能阈值, 系统提出了超高速动能弹打击侵深、成坑及地冲击安全厚度的计算方法。通过弹体侵速1 100~4 200 m/s的(超)高速侵彻实验, 验证了理论计算公式的准确性。Abstract: The hypervelocity kinetic energy weapon that strikes the ground at the speed from 5 Mach to 15 Mach has some unique characteristics of penetration mechanism and damage effects, which cannot be accurately described by ths existing theories.In this paper, the dynamic compressibility behavior of rock, penetration and explosion effects in the near zone is systematically summarized.It is found that the actual stress in the rock impacted under velocity of 5 Mach to 15 Mach is between fluid state and elasto-plasticity state.A theoretical model of hydro-elastoplastic-frictional penetration model is proposed, which fills the gap of stress state between elastic-plastic state and hydro-dynamic state.For the first time, the impedance formula is obtained, which can describe the stress state of whole interaction process between target and projectile.The minimum kinetic energy threshold of solid penetration, pseudofluid penetration and fluid penetration is defined.The methods for calculating hypervelocity impact effects including penetration depth, crater radius and the safety thickness of protective layer are proposed in the paper.In addition, the accuracy of the theoretical formula is verified by a series of penetration tests with the impact speed from 1 100 m/s to 4 200 m/s.
-
图 1 球形弹超高速撞击下介质中压力分布
Figure 1. Pressure distribution in medium under hypervelocity impact of spherical projectile
图 3 材料强度对应变率的依赖规律
Figure 3. Dependent relationship of material strength to strain rate
图 4 弹性区域、内摩擦区域和塑性流动区域
Figure 4. Elastic region, internal friction region and plastic flow region
图 5 计算得到的α*(ε)、σ(ε)、p(ε)、τ(ε)曲线
Figure 5. Calculated curves of α*(ε), σ(ε), p(ε), τ(ε)
图 6 侵彻速度界定及介质压缩状态
Figure 6. Definition the scope of penetration velocity and medium compression state
图 8 超高速弹体侵彻岩石成坑范围
Figure 8. Crater range of rocks penetrated by hyper-velocity projectile
图 12 不同侵彻速度条件下弹体侵蚀状态
Figure 12. Erosion status of projectile under different impact velocities
图 13 侵彻深度计算结果与实验结果对比
Figure 13. Comparison of calculating and experimental results of penetration depth
图 14 径向裂纹区半径计算结果与实验结果对比
Figure 14. Comparison of crater radius between calculating and experimental results
图 15 弹速3 558 m/s靶体各层地冲击压力时程曲线
Figure 15. Profile of ground shock in each layer with impact velocity 3 558 m/s
图 16 弹速3 558 m/s靶体各层地冲击波衰减规律
Figure 16. Attenuation law of the ground shock wave in target with impact velocity 3 558 m/s
图 17 等效装药爆炸应力波时程曲线
Figure 17. Time history curves of equivalent charge explosion stress wave
图 19 超高速弹丸撞击花岗岩的最小防护层厚度
Figure 19. Minimum thickness of protective layer for impact of hypervelocity projectile on granite
岩石类型 花岗岩 片麻-花岗岩 石英岩 板岩 石灰岩 砂岩 τp/GPa 0.97~1.19 0.68 0.61 0.48~0.57 0.87~1.02 0.90 
下载: 导出CSV
表 2 第一阶段实验测试结果
Table 2. Test results of the first phase
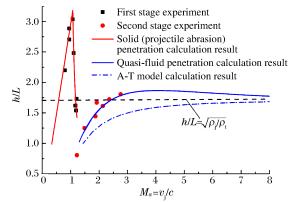
序号 发射速度/(m/s) 发射速度Ma 侵彻深度h/L 弹体残余质量m/mj 1 1 196 0.798 2.200 0.975 2 1 426 0.951 2.704 0.968 3 1 430 0.953 2.885 0.965 4 1 600 1.067 3.035 0.950 5 1 654 1.103 2.481 0.950 6 1 752 1.168 1.619 0.313 7 1 789 1.193 1.539 0.288 8 1 808 1.205 1.730 0.316
下载: 导出CSV
表 3 第二阶段实验综合量测结果
Table 3. Test results of the second phase
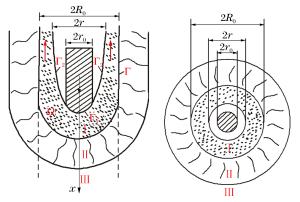
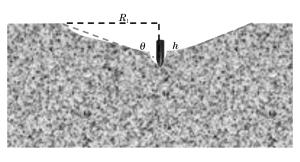
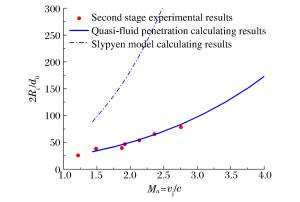
序号 发射速度/(m/s) 发射速度Ma 侵彻深度h/L 靶体表面破碎区直径Rc/d0 1 1 829.4 1.220 0.806 25.69 2 2 231.0 1.487 1.250 38.19 3 2 600.3 1.734 0.861 36.81 4 2 806.9 1.871 1.444 39.58 5 2 878.2 1.919 1.667 46.53 6 3 199.6 2.133 1.611 53.82 7 3 542.1 2.361 1.722 65.28 8 4 135.6 2.757 1.806 78.47 注:序号3实验结果异常,未列入图13中。
下载: 导出CSV
-
[1] 钱七虎, 王明洋.岩土中的冲击爆炸效应[M].北京:国防工业出版社, 2010:1-43. [2] 任辉启.精确制导武器侵彻效应与工程防护[M].北京:科学出版社, 2016:1-25. [3] SHEMYAKIN E I.Physical and mechanical fundamentals of unconventional technologies of solid mineral development[J].Physical Mesomechanics, 2007, 10(1/2):87-93. [4] 哈努卡耶夫.矿岩爆破物理过程[M].刘殿中, 译.北京: 冶金工业出版社, 1980: 63-82. [5] MELSOSH H J.Impact ejection, spallation, and the origin of meteorites[J].Icarus, 1984, 59(2):234-260. doi: 10.1016/0019-1035(84)90026-5 [6] FORRESTAL M J, TZOU D Y.A spherical cavity-expansion penetration model for concrete targets[J].International Journal of Solids and Structures, 1997, 34(31/32):4127-4146. http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0226220945/ [7] FORRESTAL M J, LUK V K.Dynamic spherical cavity-expansion in a compressible elastic-plastic solid[J].Journal of Applied Mechanics, 1988, 55(2):275-279. doi: 10.1115/1.3173672 [8] VOITISHEK Y V, SLEPYAN L I.Hydrodynamic model of the puncture of a brittle plate[J].Soviet Mining, 1985, 21(3):231-235. doi: 10.1007/BF02500973 [9] SLEPYAN L I.Calculation of the size of the crater formed by a high-speed impact[J].Journal of Mining Science, 1978, 14(5):465-471. doi: 10.1007%2FBF01086757 [10] ROSENBERG Z, MARMOR E, MAYSELESS M.On the hydrodynamic theory of long-rod penetration[J].International Journal of Impact Engineering, 1990, 10(1/2/3/4):483-486. doi: 10.1016-0734-743X(90)90081-6/ [11] 舍米亚金Е И.弹塑性理论的动力学问题[M].戚承志, 译.北京: 科学出版社, 2009: 101-106. [12] SHEMYAKIN E I.Behavior of rocks under dynamic loads[J].Soviet Mining, 1966, 2(1):8-14. doi: 10.1007/BF02497092 [13] ZENG H, BAI H, ZHU T.X-51A scramjet engine flight and demonstration program[J].Missiles & Space Vehicles, 2010, 29(1):57-61. http://d.old.wanfangdata.com.cn/Periodical/ddyhtyzjs201001012 [14] 李益翔.美国高超声速飞行器发展历程研究[D].哈尔滨: 哈尔滨工业大学, 2016. [15] 李争, 刘元雪, 胡明, 等."上帝之杖"天基动能武器毁伤效应评估[J].振动与冲击, 2016, 35(18):159-164. http://d.old.wanfangdata.com.cn/Periodical/zdycj201618026LI Zheng, LIU Yuanxue, HU Ming, et al.Damage effect evaluation of God stick space-based kinetic energy weapons[J].Journal of Vibration and Shock, 2016, 35(18):159-164. http://d.old.wanfangdata.com.cn/Periodical/zdycj201618026 [16] ZHOU Y X, XIA K, LI X B, et al.Suggested methods for determining the dynamic strength parameters and mode-I fracture toughness of rock materials[J].International Journal of Rock Mechanics & Mining Sciences, 2011, 49(1):105-112. https://www.deepdyve.com/lp/elsevier/suggested-methods-for-determining-the-dynamic-strength-parameters-and-f01d0RBz3P [17] 奥尔连科Л П.爆炸物理学[M].孙承纬, 译.北京: 科学出版社, 2011: 1127-1152. [18] 泽尔道维奇Я Б, 莱依健尔Ю Л.激波和高温流体动力学现象物理学(下册)[M].张树才, 译.北京: 科学出版社, 1985: 234-260. [19] 戚承志, 钱七虎.岩石等脆性材料动力强度依赖应变率的物理机制[J].岩石力学与工程学报, 2003, 22(2):177-181. doi: 10.3321/j.issn:1000-6915.2003.02.002QI Chengzhi, QIAN Qihu.Physical mechanism of dependence of material strength on strain rate for rock-like material[J].Chinese Journal of Rock Mechanics and Engineering, 2003, 22(2):177-181. doi: 10.3321/j.issn:1000-6915.2003.02.002 [20] 戚承志, 钱七虎.岩体动力变形与破坏的基本问题[M].北京:科学出版社, 2009. [21] LUNDBORG N.Strength of rock-like materials[J].International Journal of Rock Mechanics and Mining Science, 1968, 5(5):427-454. doi: 10.1016/0148-9062(68)90046-6 [22] ALEKSEEVSKⅡ V P.Penetration of a rod into a target at high velocity[J].Combustion, Explosion, and Shock Waves, 1966, 2(2):99-106. doi: 10.1007-BF00749237/ [23] TATE A.A theory for the deceleration of long rods after impact[J].Journal of the Mechanics and Physics of Solids, 1967(15):387-399. doi: 10.1016-0022-5096(69)90028-3/ [24] TATE A.Long rod penetration models-part I.a flow field model for high speed long rod penetration[J].International Journal of Mechanical Sciences, 1986, 28(8):535-548. doi: 10.1016/0020-7403(86)90051-2 [25] 王明洋, 邱艳宇, 李杰, 等.超高速长杆弹对岩石侵彻、地冲击效应理论与实验研究[J].岩石力学与工程学报, 2018, 37(3):564-572.WANG Mingyang, QIU Yanyu, LI Jie, et al.Theoretical and experimental study on penetration in rock and ground impact effects of long rod projectiles of hyper speed[J].Chinese Journal of Rock Mechanics and Engineering, 2018, 37(3):564-572. [26] 李干, 宋春明, 邱艳宇, 等.超高速弹对花岗岩侵彻深度逆减现象的理论与实验研究[J].岩石力学与工程学报, 2018, 37(1):60-66. http://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201801006.htmLI Gan, SONG Chunming, QIU Yanyu, et al.Theoretical and experimental studies on the phenomenon of reduction in penetration depth of hyper-velocity projectiles into granite[J].Chinese Journal of Rock Mechanics and Engineering, 2018, 37(1):60-66. http://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201801006.htm [27] 宋春明, 李干, 王明洋, 等.不同速度段弹体侵彻岩石靶体的理论分析[J].爆炸与冲击, 2018, 38(2):250-257. http://www.bzycj.cn/CN/abstract/abstract9882.shtmlSONG Chunming, LI Gan, WANG Mingyang, et al.Theoretical analysis of projectiles penetrating into rock targets at different velocities[J].Explosion and Shock Waves, 2018, 38(2):250-257. http://www.bzycj.cn/CN/abstract/abstract9882.shtml [28] GUREVICH M I.The theory of jets of an ideal fluid[M].Moscow:Nauka, 1979:536-537. [29] SHISHKIN N I.Seismic efficiency of a contanct explosion and a high-velocity impact[J].Journal of Applied Mechanics and Technical Physics, 2007, 48(2):145-152. doi: 10.1007/s10808-007-0019-6 [30] VOITISHEK Y V, SLEPYAN L I.Hydrodynamic model of the puncture of a brittle plate[J].Soviet Mining, 1985, 21(3):231-235. doi: 10.1007/BF02500973 [31] 邓国强, 杨秀敏.超高速武器对地打击效应数值仿真[J].科技导报, 2015, 33(16):65-71. doi: 10.3981/j.issn.1000-7857.2015.16.010DENG Guoqiang, YANG Xiumin.Numerical simulation of ground impact effects of hypervelocity weapons[J].Science and Technology Herald, 2015, 33(16):65-71. doi: 10.3981/j.issn.1000-7857.2015.16.010 [32] 邓国强, 杨秀敏.超高速武器对地打击效应特点分析[C]//第一届全国超高速碰撞会议论文集.四川绵阳: 中国空气动力研究与发展中心, 2013: 141-144. [33] 邓国强, 杨秀敏.超高速武器流体侵彻与装药浅埋爆炸效应的等效方法[J].防护工程, 2015, 37(6):27-32.DENG Guoqiang, YANG Xiumin.Effect equivalent method between fluid penetration of hyper velocity weapon and shallow detonation of explosive[J].Protective Engineering, 2015, 37(6):27-32. [34] U.S.Army Engineer Waterways Experiment Station.Fundamentals of protective design for conventional weapons: Tm-855-1[R].Vicksburg, Mississippi, 1986. -
计量
- 文章访问数: 5272
- HTML全文浏览量: 1731
- PDF下载量: 99
- 被引次数: 0