梯度密度黏弹性材料的波传播研究

李毅; 苗春贺; 徐松林; 张金咏; 王鹏飞

doi:10.11883/bzycj-2020-0313

梯度密度黏弹性材料的波传播研究

doi: 10.11883/bzycj-2020-0313

李毅^1,,
苗春贺¹,
徐松林^{1, 2, ,},
张金咏³,
王鹏飞¹

1.
中国科学技术大学中国科学院材料力学行为和设计重点实验室，安徽合肥 230027
2.
中国地震局地震预测研究所高压物理与地震科技联合实验室，北京 100036
3.
武汉理工大学材料复合新技术国家重点实验室，湖北武汉 430070

基金项目: 高压物理与地震科技联合实验室室开放基金（2019HPPES01）；国家自然科学基金（11672286，11602267，11872361）；安徽省自然科学基金（1708085MA05）

详细信息

作者简介:
李　毅（1996－　），男，硕士，ustcliyi@mail.ustc.edu.cn

通讯作者:
徐松林（1971－　），男，博士，研究员，博士生导师，slxu99@ustc.edu.cn

中图分类号: O347.4
计量
- 文章访问数: 758
- HTML全文浏览量: 446
- PDF下载量: 98
- 被引次数: 0
出版历程
- 收稿日期: 2020-08-31
- 修回日期: 2020-10-20
- 刊出日期: 2021-01-05

Wave propagation in density-graded viscoelastic material

1.
CAS Key Laboratory of Mechanical Behavior and Design of Materials, University of Science and Technology of China, Hefei 230027, Anhui, China
2.
United Laboratory of High Pressure Physics and Earthquake Science, Institute of Earthquake Forecasting, China Earthquake Administration，Beijing 100036, China
3.
State Key Laboratory of Advanced Technology for Materials Synthesis and Processing,Wuhan University of Technology, Wuhan 430070, Hubei, China

摘要

摘要: 梯度密度黏弹性材料中波的传播比较复杂。为了研究其在冲击载荷作用下黏弹性响应特征，基于控制方程的Euler形式，利用Laplace变换，得到了这种材料中的波传播规律的一个理论公式；并据此分析了双层周期性黏弹性介质中的应力情况。选择具有梯度密度特性的钛-硼化钛（Ti-TiB₂）材料和碳纤维树脂材料，采用不同的叠合方向和方式，利用分离式霍普金森压杆（split Hopkinson pressure bar，SHPB）加载装置进行了动态冲击实验，并用三波法对得到的实验结果进行处理。同时，采用数值Laplace逆变换方法，结合SHPB测得的入射波与透射波数据，使用推导的理论公式计算出理论解，并与实验结果进行了比较。结果表明：（1）梯度钛-硼化钛材料由于内界面和叠层界面的存在，表现出一定的黏性特性；单层Ti-TiB₂材料的计算结果和三波法分析得到的结果基本一致，双层Ti-TiB₂材料叠合后的计算结果与三波法分析结果存在一定的差异。（2）双层碳纤维树脂材料表现出较强的黏弹性特征，应力波的衰减幅度较大，三波法分析结果与该材料的冲击性能有较大的差异。由此可知，无论是细微观结构特征产生的黏性，还是材料本身的黏性，对材料动力学行为的影响都不可忽略。。
- 梯度密度 /
- 黏弹性材料 /
- 多层材料 /
- 冲击性能
Abstract: Wave propagation in visco-elastic materials with gradient density is really complex. In order to understand the responses of the visco-elastic materials to impact load, a series of theoretical equations for wave propagation in density-graded visco-elastic materials were proposed by employing the Euler form of the governing equations and the Laplace transform method. According to these equations, the wave propagation in the two-layer periodically-superimposed media with perpendicular incidence was analyzed. The Ti-TiB₂ material with gradient density characteristics and the carbon-fiber-reinforced resin composites with strong visco-elastic properties were selected as experimental subjects to carry out dynamic impact tests by applying a split Hopkinson pressure bar (SHPB) device. To better reflect the influences of the gradient characteristics on the dynamic responses of the materials, the experimental specimens were prepared by using different stacking directions and modes. The data obtained by the SHPB device were analyzed by the three-wave method. Moreover, according to the incident wave and transmission wave obtained by the SHPB device, the wave propagation equations proposed for the visco-elastic media with gradient density were applied to obtain the corresponding theoretical solutions. And the calculated theoretical solutions were compared with the experimental results. The comparisons display as follows. (1) Due to the internal interface and the superimposed interface, the graded Ti-TiB₂ materials show certain viscosity properties. For single-layer Ti-TiB₂ specimens, the theoretically calculated results are approximately consistent with the experimental ones analyzed by the three-wave method. But there lie some differences for two-layer Ti-TiB₂ specimens. (2) The two-layer carbon fiber reinforced resin composites exhibit stronger visco-elastic characteristics, and the attenuation amplitude of stress wave is larger. There are obvious differences between the experimental results analyzed by the three-wave method and theoretically calculated ones. As a consequence, the influences of the viscosity produced by the meso-structures and the viscosity of the material itself on the dynamic behaviors of the macro medium cannot be ignored.
- gradient density /
- viscoelastic material /
- multilayer material /
- impact properties

HTML全文

图 1 垂直入射双层周期性叠合介质示意图

Figure 1. Schematic diagram of a two-layer periodically-superimposed medium with normal incidence

下载: 全尺寸图片幻灯片

图 2 梯度钛-硼化钛样品中密度和硬度^[16]分布

Figure 2. Distributions of density and hardness^[16] in gradient Ti-TiB₂ specimen

下载: 全尺寸图片幻灯片

图 3 梯度钛-硼化钛实验波形

Figure 3. Recorded wave profiles in the gradient Ti-TiB₂ specimens

下载: 全尺寸图片幻灯片

图 4 单层试件中的应力波形

Figure 4. Stress-time curves in single-layer specimens

下载: 全尺寸图片幻灯片

图 5 双层叠合试件中的应力波形

Figure 5. Stress-time curves in two-layer superimposed specimens

下载: 全尺寸图片幻灯片

图 6 制备的碳纤维增强树脂复合材料的密度随碳纤维质量分数的变化

Figure 6. Density change of prepared carbon-fiber reinforced resin composites with carbon fiber mass fraction

下载: 全尺寸图片幻灯片

图 7 双层碳纤维增强树脂叠合试件中的应力波形

Figure 7. Stress-time curves in two-layer superimposed specimens of carbon fiber reinforced resin

下载: 全尺寸图片幻灯片

图 8 等效梯度密度材料和双层叠合试件中的应力波形的对比

Figure 8. Comparison of stress-time curves in the equivalent gradient-density materials with those in two-layer superimposed specimens

下载: 全尺寸图片幻灯片

参考文献(18)

[1]	徐松林, 刘永贵, 席道瑛, 等. 弹性波在含双裂纹岩体中的传播分析 [J]. 地球物理学报, 2012, 55(3): 944–952. DOI: 10.6038/j.issn.0001-5733.2012.03.024. XU S L, LIU Y G, XI D Y, et al. Analysis of propagation of elastic wave in rocks with double-crack model [J]. Chinese Journal of Geophysics, 2012, 55(3): 944–952. DOI: 10.6038/j.issn.0001-5733.2012.03.024.
[2]	谭子翰, 徐松林, 刘永贵, 等. 含多种尺寸缺陷岩体中的弹性波散射 [J]. 应用数学和力学, 2013, 34(1): 38–48. DOI: 10.3879/j.issn.1000-0887.2013.01.005. TAN Z H, XU S L, LIU Y G, et al. Scattering of elastic waves by multi-size defects in rock mass [J]. Applied Mathematics and Mechanics, 2013, 34(1): 38–48. DOI: 10.3879/j.issn.1000-0887.2013.01.005.
[3]	胡时胜, 王礼立, 宋力, 等. Hopkinson压杆技术在中国的发展回顾 [J]. 爆炸与冲击, 2014, 34(6): 641–657. DOI: 10.11883/1001-1455(2014)06-0641-17. HU S S, WANG L L, SONG L, et al. Review of the development of Hopkinson pressure bar technique in China [J]. Explosion and Shock Waves, 2014, 34(6): 641–657. DOI: 10.11883/1001-1455(2014)06-0641-17.
[4]	ZHAO H, GARY G, KLEPACZKO J R. On the use of a viscoelastic split Hopkinson pressure bar [J]. International Journal of Impact Engineering, 1997, 19(4): 319–330. DOI: 10.1016/S0734-743X(96)00038-3.
[5]	BACON C. An experimental method for considering dispersion and attenuation in a viscoelastic Hopkinson bar [J]. Experimental Mechanics, 1998, 38(4): 242–249. DOI: 10.1007/BF02410385.
[6]	王宝珍, 胡时胜. 猪肝动态力学性能及本构模型研究 [J]. 力学学报, 2017, 49(6): 1399–1408. DOI: 10.6052/0459-1879-17-238. WANG B Z, HU S S. Research on dynamic mechanical response and constitutive model of porcine liver [J]. Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(6): 1399–1408. DOI: 10.6052/0459-1879-17-238.
[7]	朱珏, 胡时胜, 王礼立. SHPB试验中粘弹性材料的应力均匀性分析 [J]. 爆炸与冲击, 2006, 26(4): 315–322. DOI: 10.11883/1001-1455(2006)04-0315-08. ZHU J, HU S S, WANG L L. Analysis on stress uniformity of viscoelastic materials in split Hopkinson bar tests [J]. Explosion and Shock Waves, 2006, 26(4): 315–322. DOI: 10.11883/1001-1455(2006)04-0315-08.
[8]	王礼立. 应力波基础[M]. 2版. 北京: 国防工业出版社, 2005: 148−177. WANG L L. Foundation of stress waves [M]. 2nd ed. Beijing: National Defense Industry Press, 2005: 148−177.
[9]	TING T C T, MUKUNOKI I. A theory of viscoelastic analogy for wave propagation normal to the layering of a layered medium [J]. Journal of Applied Mechanics, 1979, 46(2): 329–336. DOI: 10.1115/1.3424550.
[10]	TEDESCO J W, LANDIS D W. Wave propagation through layered systems [J]. Computers & Structures, 1989, 32(3/4): 625–638. DOI: 10.1016/0045-7949(89)90351-9.
[11]	HAN C, SUN C T. Attenuation of stress wave propagation in periodically layered elastic media [J]. Journal of Sound and Vibration, 2001, 243(4): 747–761. DOI: 10.1006/jsvi.2000.3420.
[12]	MUKERJI T. Waves and scales in heterogeneous rocks [D]. Stanford: Stanford University, 1995.
[13]	周风华, 陈亮. SHPB实验中粘弹性试件内部应力波的传播 [J]. 固体力学学报, 2010, 31(2): 149–156. DOI: 10.19636/j.cnki.cjsm42-1250/o3.2010.02.006. ZHOU F H, CHEN L. Stress wave propagations in viscoelastic specimen during SHPB tests [J]. Chinese Journal of Solid Mechanics, 2010, 31(2): 149–156. DOI: 10.19636/j.cnki.cjsm42-1250/o3.2010.02.006.
[14]	郑宇轩, 陈亮, 周风华, 等. Laplace变换法研究SHPB实验中试件的黏弹性波传播问题 [J]. 力学学报, 2014, 46(6): 843–852. DOI: 10.6052/0459-1879-14-002. ZHENG Y X, CHEN L, ZHOU F H, et al. Using Laplace transform to solve the viscoelastic wave problems in the SHPB experiments [J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(6): 843–852. DOI: 10.6052/0459-1879-14-002.
[15]	张鸣, 王道荣, 单俊芳, 等. 石英纤维布叠层材料冲击性能研究 [J]. 实验力学, 2018, 33(2): 183–193. DOI: 10.7520/1001-4888-17-201. ZHANG M, WANG D R, SHAN J F, et al. Investigation on impact properties of quartz fiber cloth laminated material [J]. Journal of Experimental Mechanics, 2018, 33(2): 183–193. DOI: 10.7520/1001-4888-17-201.
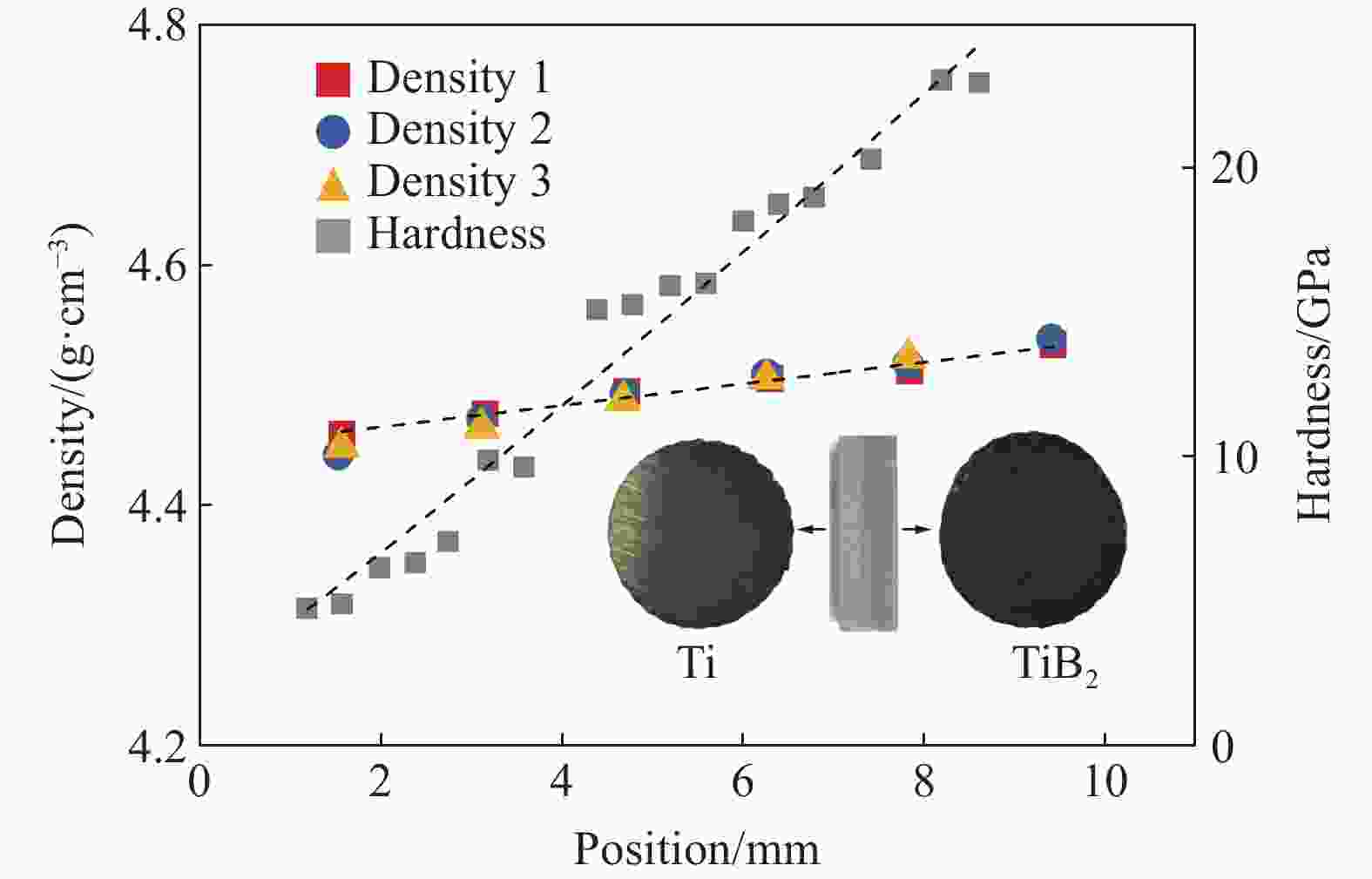
[16]	柯文轩. TiB₂-TiB-Ti梯度材料的制备与力学性能研究[D]. 武汉: 武汉理工大学, 2013. KE W X. Fabrication and mechanical properties of TiB₂-TiB-Ti functionally gradient materials [D]. Wuhan: Wuhan University of Technology, 2013.
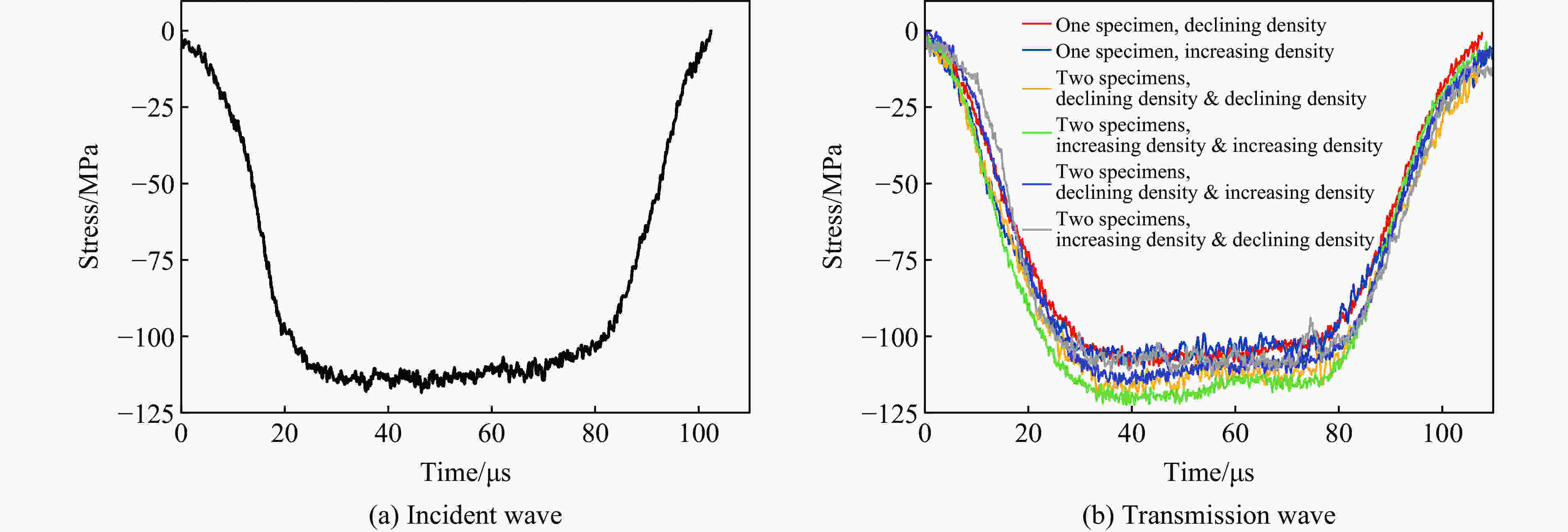
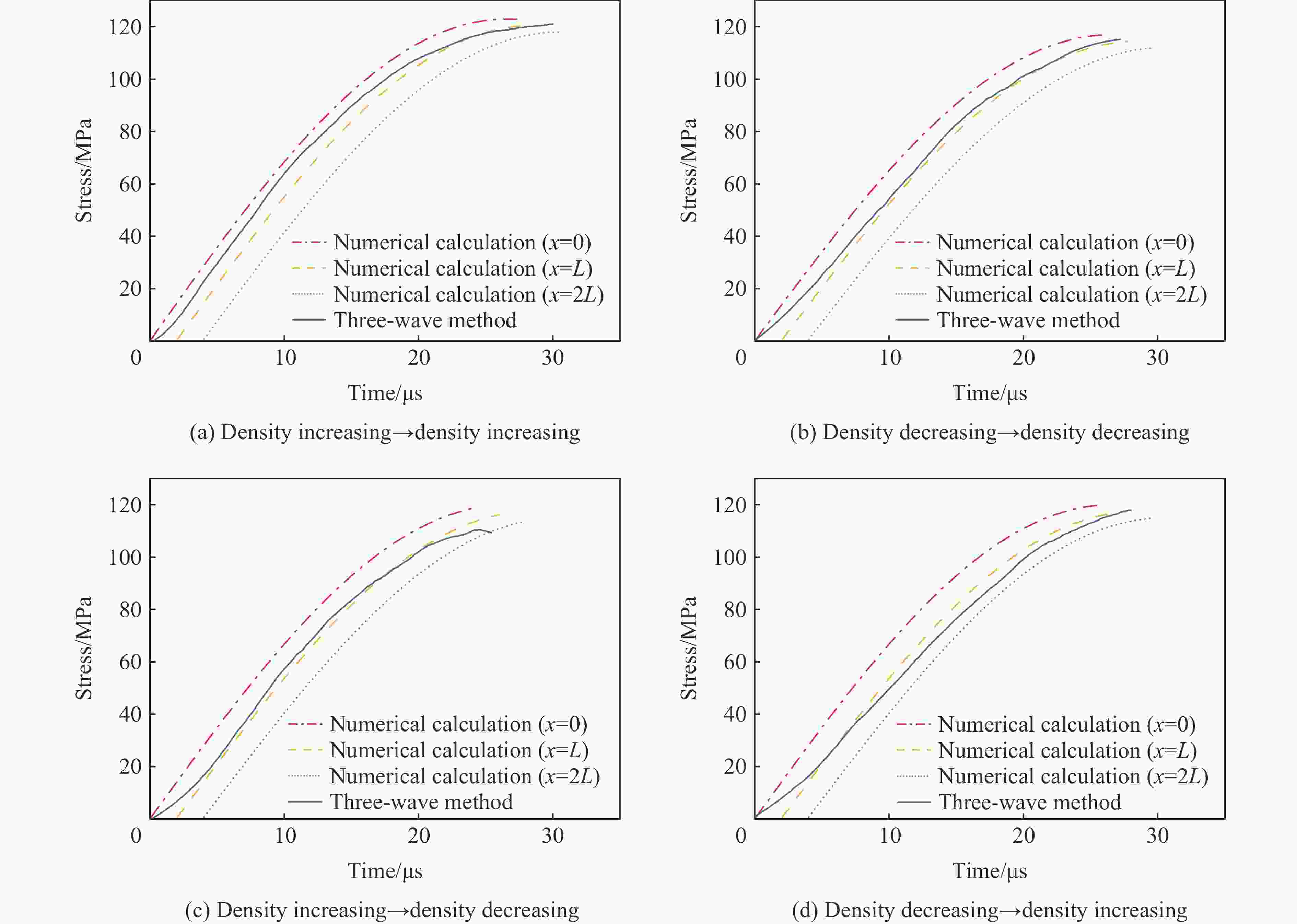
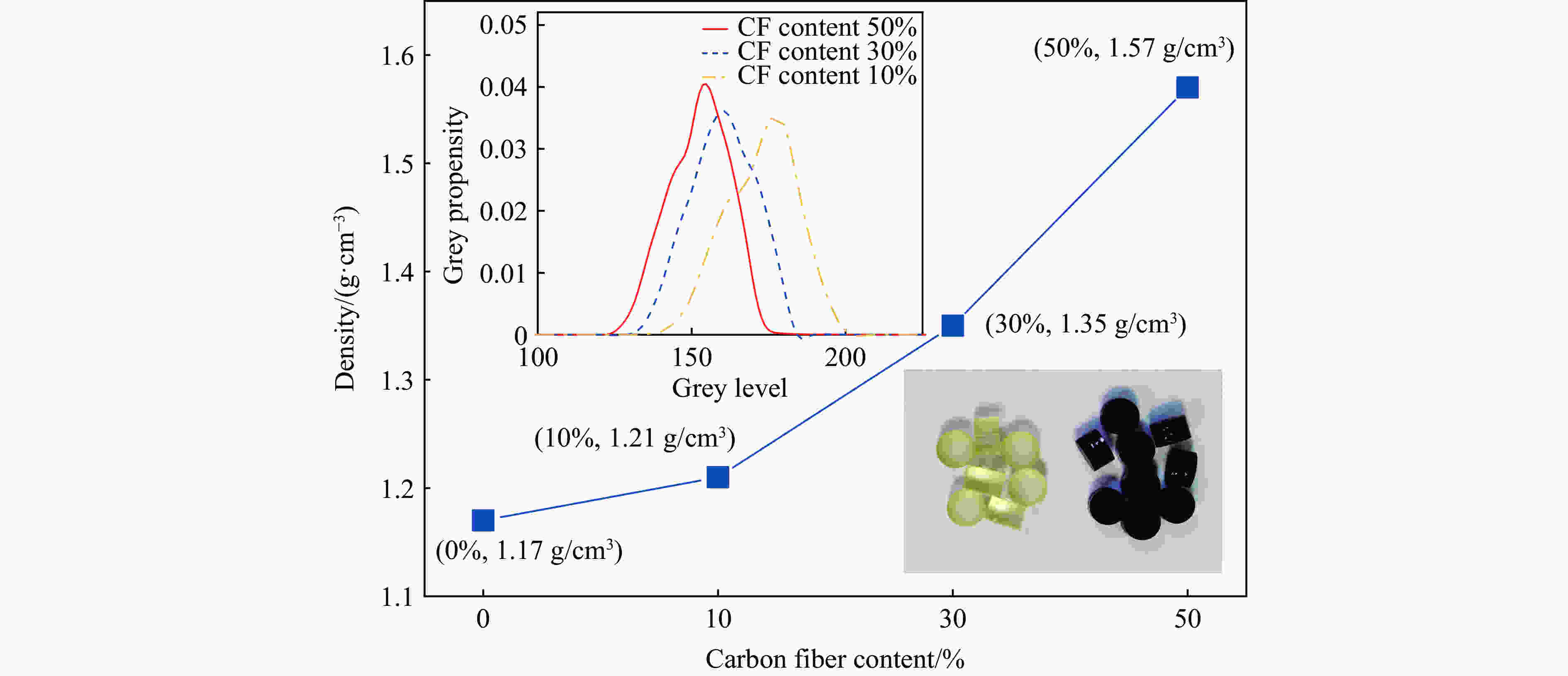
[17]	张鸣. 变密度粘弹性介质中弹性波传播的理论和实验研究[D]. 合肥: 中国科学技术大学, 2018. ZHANG M. Theoretical and experimental study on the propagation of stress wave in viscoelastic medium with variable density [D]. Hefei: University of Science and Technology of China, 2018.
[18]	周光泉, 刘孝敏. 粘弹性理论[M]. 合肥: 中国科学技术大学出版社, 1996. ZHOU G Q, LIU X M. Viscoelastic theory [M]. Hefei: University of Science and Technology of China Press, 1996.