冲击下混凝土试样应变率效应和惯性效应探讨

袁良柱; 苗春贺; 单俊芳; 王鹏飞; 徐松林

doi:10.11883/bzycj-2021-0114

冲击下混凝土试样应变率效应和惯性效应探讨

doi: 10.11883/bzycj-2021-0114

袁良柱^1,,
苗春贺¹,
单俊芳¹,
王鹏飞¹,
徐松林^{1, 2, ,}

1.
中国科学技术大学中国科学院材料力学行为和设计重点实验室，安徽合肥 230027
2.
中国地震局地震预测研究所高压物理与地震科技联合实验室，北京 100036

基金项目: 国家自然科学基金（11672286，11872361）；中央高校基本科研业务费专项（WK2480000008）；中石油与中科院重大战略合作项目（2015A-4812）；高压物理与地震科技联合实验室开放基金（2019HPPES01）

详细信息

作者简介:
袁良柱（1998－　），男，硕士，ylzustcedu@mail.ustc.edu.cn

通讯作者:
徐松林（1971－　），男，博士，研究员，博士生导师，slxu99@ustc.edu.cn

中图分类号: O382
计量
- 文章访问数: 541
- HTML全文浏览量: 827
- PDF下载量: 191
- 被引次数: 0
出版历程
- 收稿日期: 2021-04-01
- 修回日期: 2021-06-02
- 网络出版日期: 2021-12-02
- 刊出日期: 2022-01-20

On strain-rate and inertia effects of concrete samples under impact

1.
CAS Key Laboratory for Mechanical Behavior and Design of Materials, University of Science and Technology of China, Hefei 230027, Anhui, China
2.
United Laboratory of High-Pressure Physics and Earthquake Science, Institute of Earthquake Science, China Earthquake Administration, Beijing 100036, China

摘要

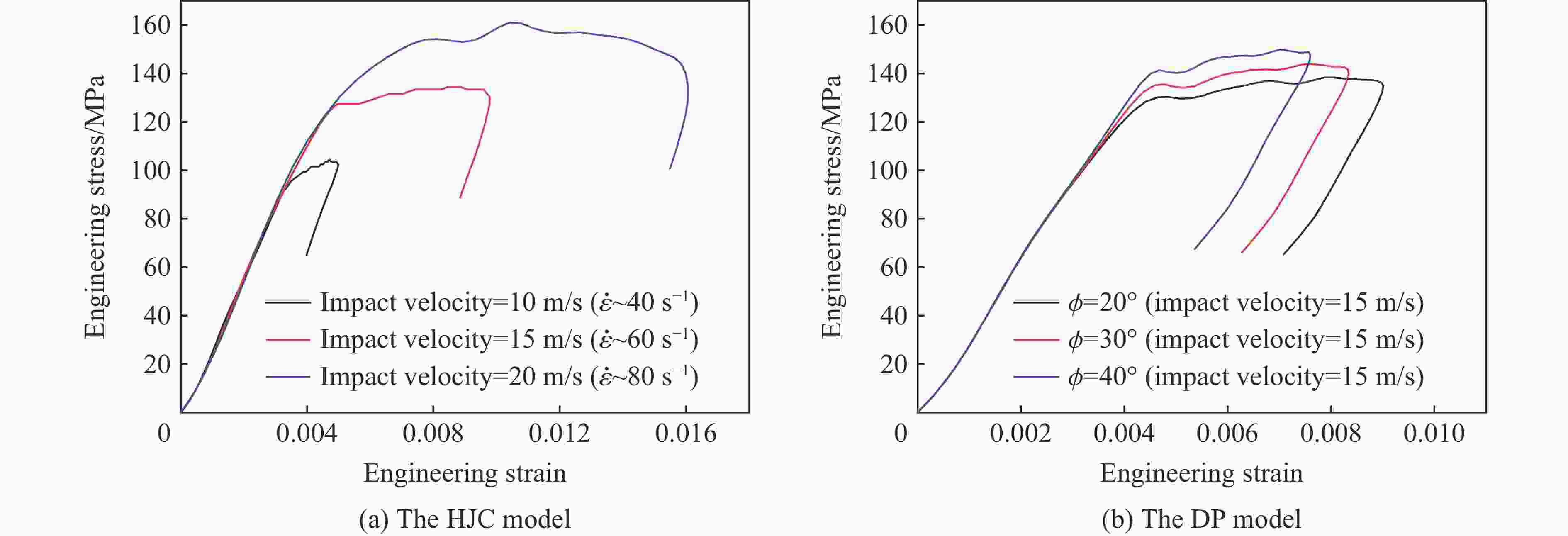
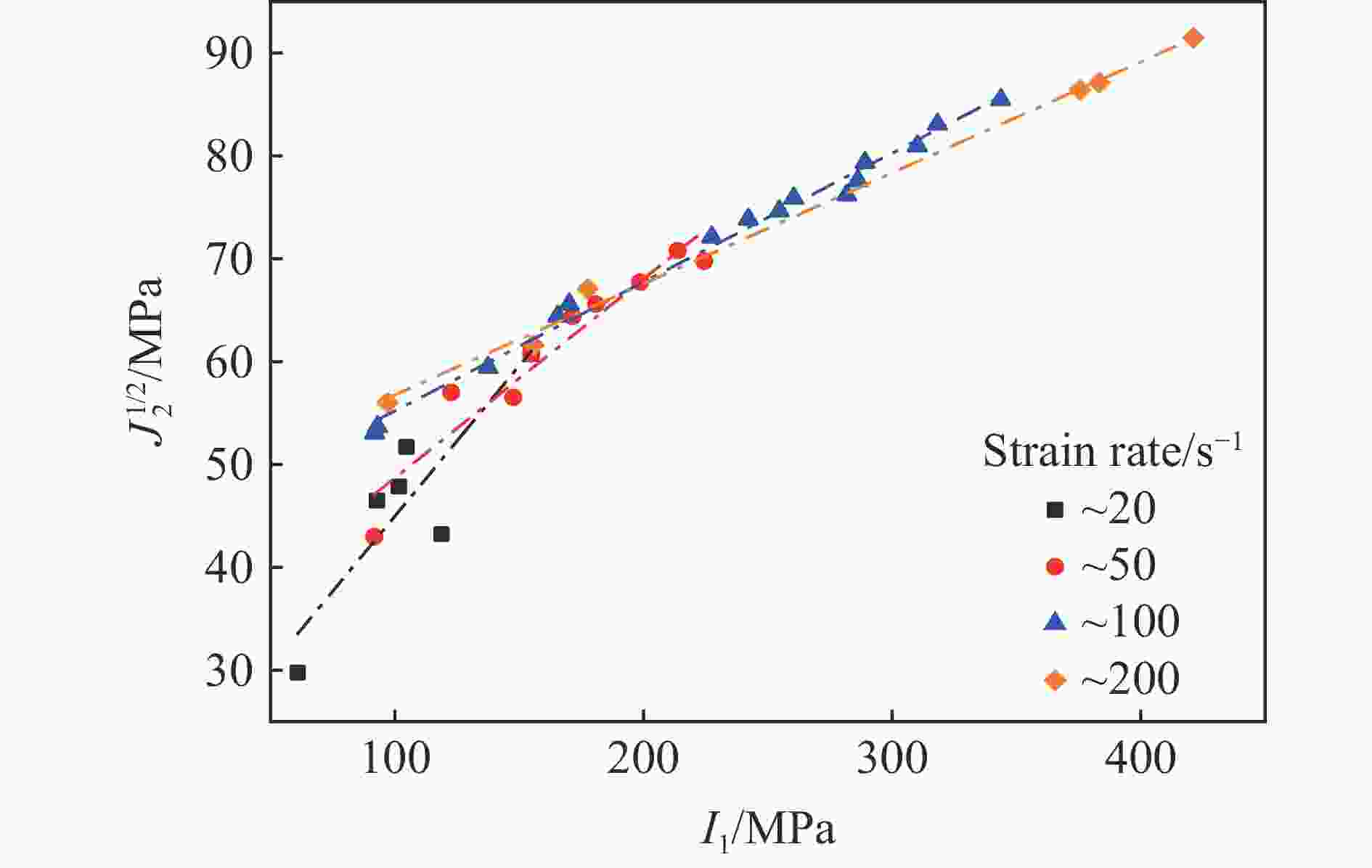
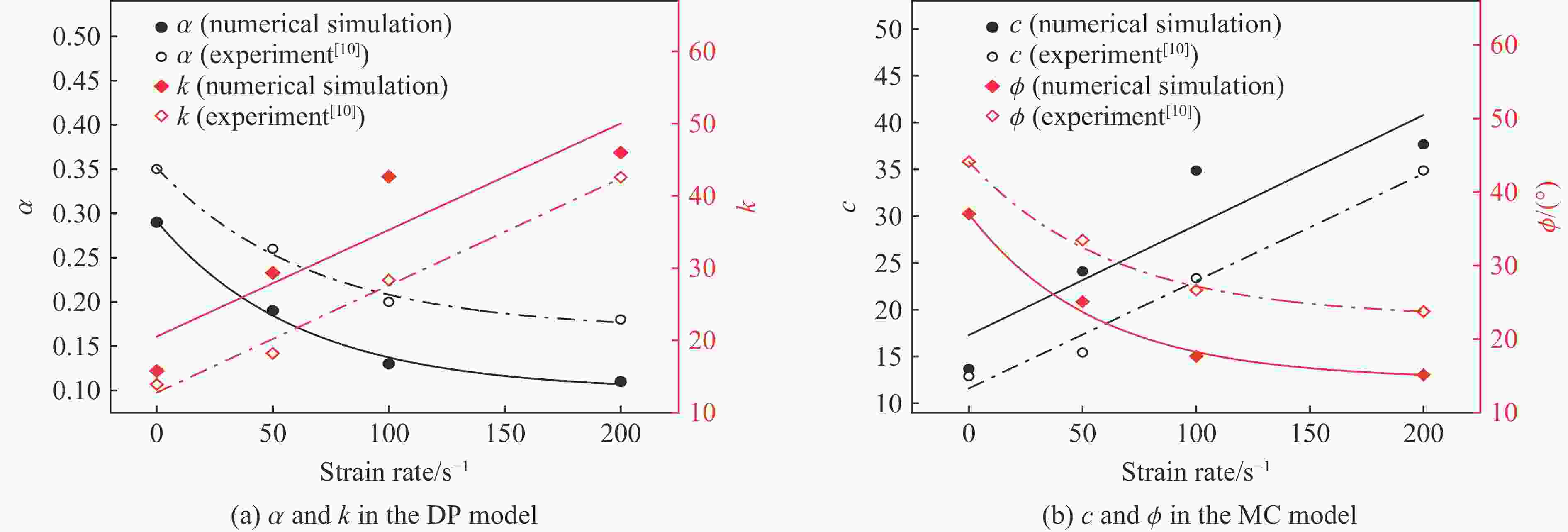
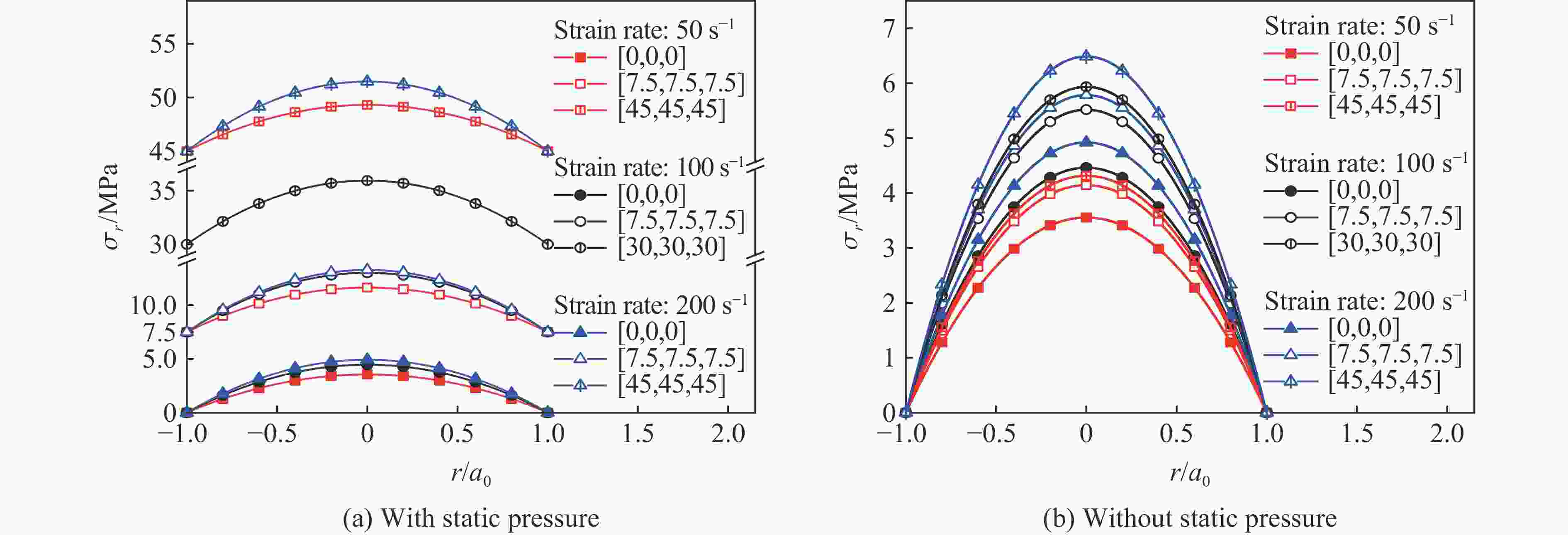
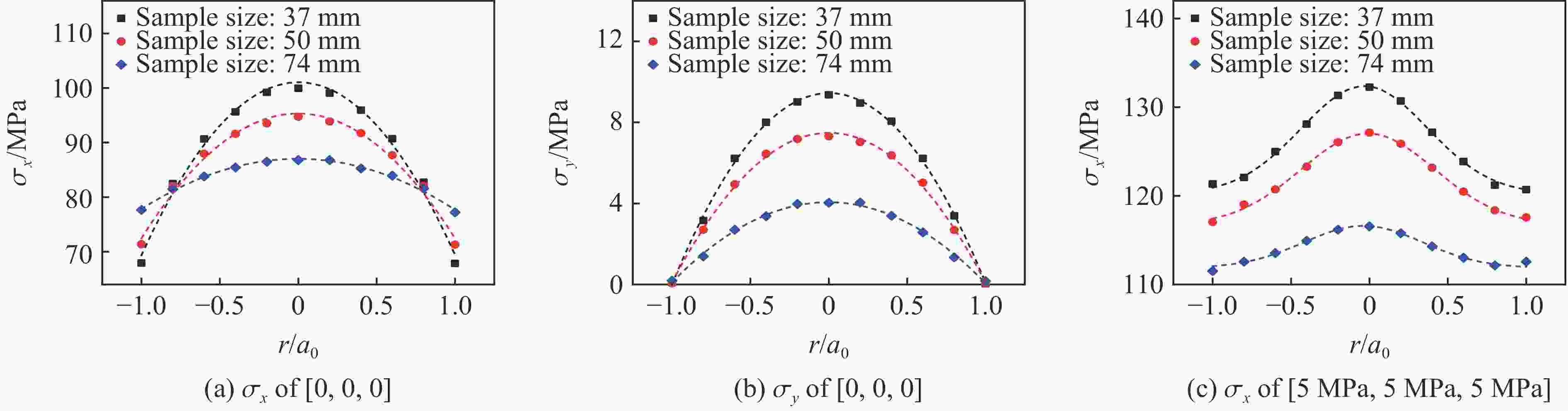
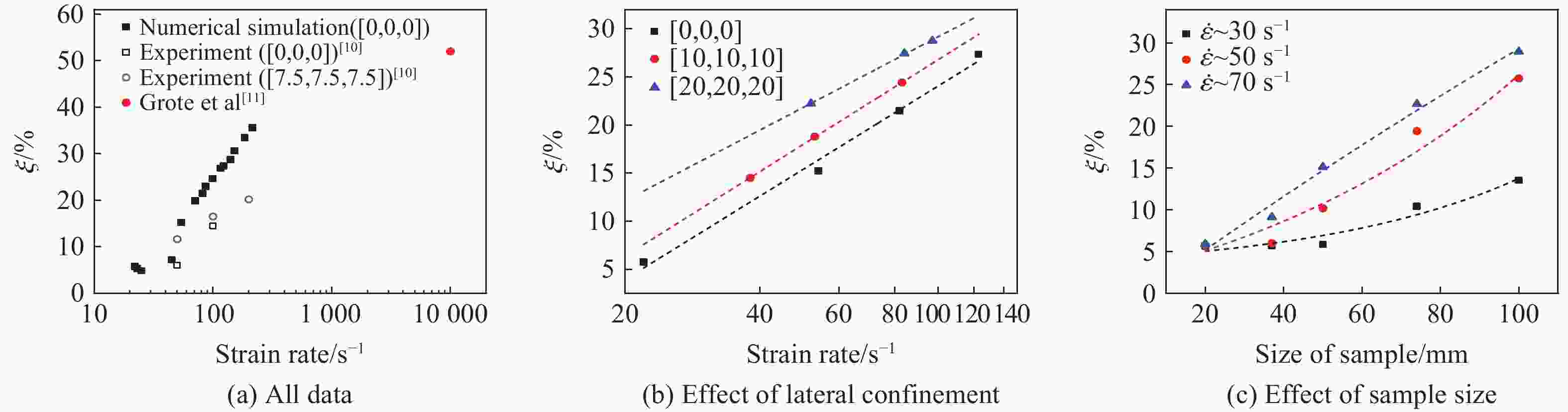
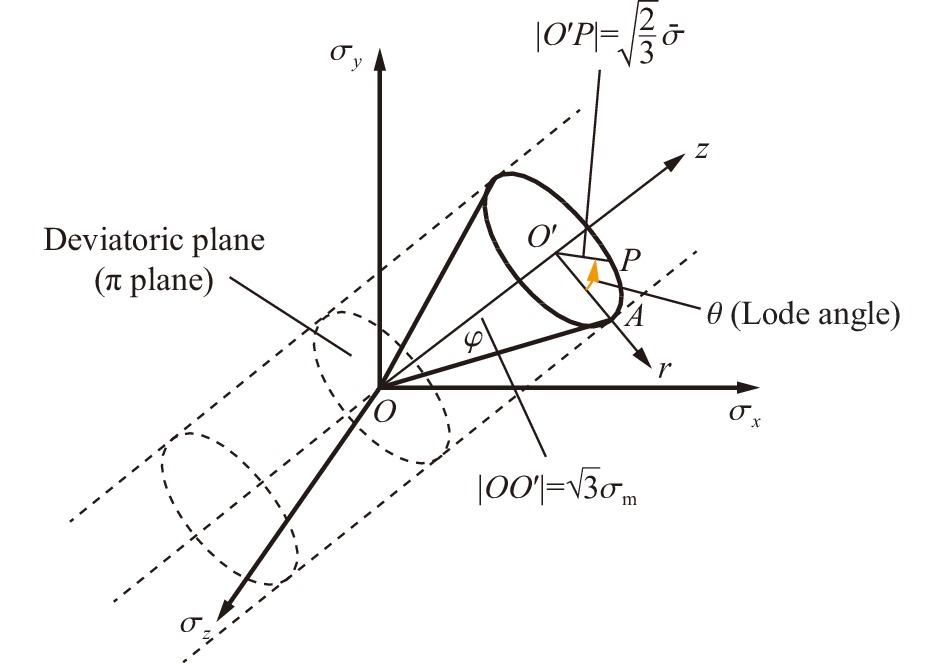
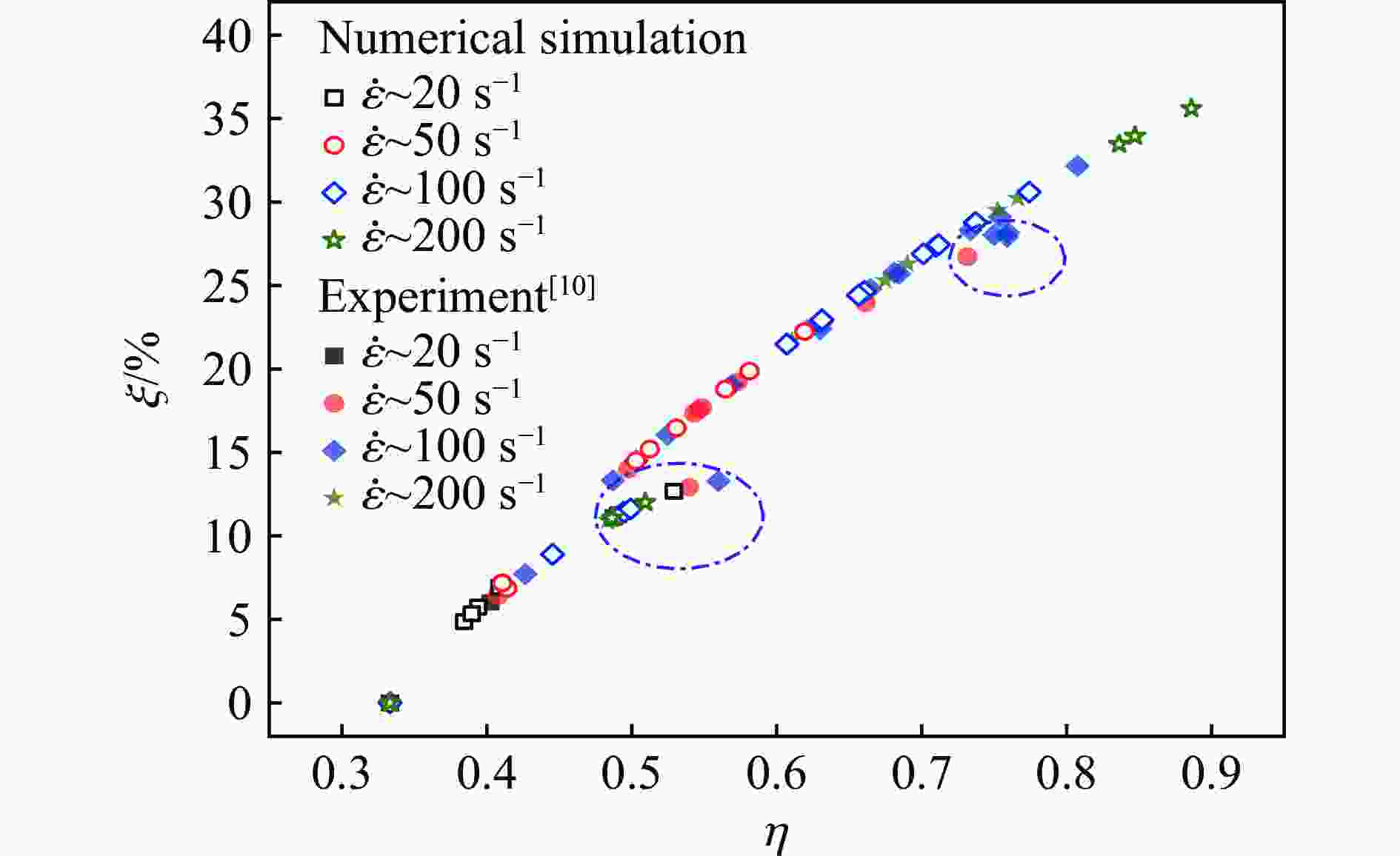
摘要: 结合混凝土试件的真三轴静载冲击实验结果，分别运用考虑应变率效应的Holmquist-Johnson-Cook (HJC)模型和考虑静水压效应的Drucker-Prager (DP)模型进行数值分析，以探讨研究混凝土试样应变率效应和惯性效应的方法。在探究混凝土的应变率效应和横向惯性效应的关系时，使用HJC模型的数值模拟结果来拟合DP准则的各个参数。结果表明：随着应变率的升高，混凝土的强度会提高，并且这种强度的提高，也有一部分原因是第一应力不变量I₁的增大所导致的。因此，混凝土试件的应变率效应和横向惯性约束具有较强的耦合作用。理论和数值分析了冲击下试样内部的横向应力分布特征与应变率、静水压和试样尺寸的关系，结果发现：试样内部横向应力的幅值随着应变率、静水压的升高而增大，但随着试样尺寸的增大而减小。为了探讨横向惯性带来的强度提升效果，提出了一个有关冲击方向最大应力σ_x和等效应力σ_e的参数ξ，且ξ=(σ_x−σ_e)/σ_x。此参数具有尺寸效应、应变率效应和静水压效应，但是此参数与应力三轴度的关系表现出应变率无关特性，可为应变率效应的研究提供新的思路。
- 冲击动力学 /
- 混凝土 /
- 应变率效应 /
- 惯性效应 /
- 应力三轴度
Abstract: Based on the dynamic experimental results of concrete specimens under true triaxial confinement, the Holmquist-Johnson-Cook (HJC) model considering the strain rate effect and the Drucker-Prager (DP) model considering the hydrostatic pressure effect were employed for numerical analysis to explore the methods for studying the strain rate effects and inertia effects. In order to explore the relationship between the strain rate effect and the lateral inertia effect of concrete, the numerical simulation results of the HJC model were used to fit the parameters of the DP criterion, and the values of the parameters α and k at four strain rates were obtained. The relationship between the DP criterion parameters and the strain rate and hydrostatic pressure was comprehensively analyzed. The results of numerical analysis show that with the increase of strain rate, the strength of concrete increases, and this strength increase is partly due to the increase of the first stress invariant I₁. It can be concluded that the strain rate and lateral inertia constraint of concrete specimens have a strong coupling effect. The relationship between the distribution characteristics of the transverse stress and the strain rate, hydrostatic pressure and specimen size under impact are analyzed theoretically and numerically. The results show that the amplitude of the transverse stress increases with the strain rate and hydrostatic pressure, but decreases with the sample size. In order to investigate the effect of lateral inertia on the strength improvement, a parameter ξ related to the maximum stress σ_xand the equivalent stress σ_e in the impact direction, defined as ξ=(σ_x−σ_e)/σ_x, was proposed. The relationship between the strain rate, hydrostatic pressure, specimen size and the parameter ξ was analyzed by the HJC model. It is found that this parameter has evident size effect, strain rate effect and hydrostatic pressure effect. However, the relationship between the parameter ξ and the stress triaxiality shows a strain rate independent characteristic. It can provide a new way for the investigation of strain rate effect.
- impact dynamics /
- concrete /
- strain rate effect /
- inertia effect /
- stress triaxiality

HTML全文

图 1 真三轴静载混凝土冲击实验设备

Figure 1. The experimental device for concrete specimens under true tri-axial confinement

下载: 全尺寸图片幻灯片

图 2 有限元计算模型

Figure 2. The finite element calculation model

下载: 全尺寸图片幻灯片

图 3 数值模拟波形

Figure 3. Simulated wave profiles in three directions

下载: 全尺寸图片幻灯片

图 4 不同侧限条件下混凝土试样的破坏形态

Figure 4. Failure patterns of concrete samples under different confinement conditions

下载: 全尺寸图片幻灯片

图 5 2种模型模拟得到的应力-应变关系

Figure 5. Stress-strain relations simulated by two strength models

下载: 全尺寸图片幻灯片

图 6 不同应变速率下$\sqrt {{J_2}} \text{-} {I_1}$平面的强度统计

Figure 6. Statistics of the strength in the $\sqrt {{J_2}} \text{-} {I_1}$ plane at different strain rates

下载: 全尺寸图片幻灯片

图 7 计算强度参数的应变率效应

Figure 7. Strain rate effect of simulated strength parameters

下载: 全尺寸图片幻灯片

图 8 横向应力分布

Figure 8. Distribution of the transverse stress

下载: 全尺寸图片幻灯片

图 9 σ_x和σ_y的分布

Figure 9. Distributions of σ_xand σ_y

下载: 全尺寸图片幻灯片

图 10 ξ的应变率效应

Figure 10. Strain rate effect of ξ

下载: 全尺寸图片幻灯片

图 11 主应力空间

Figure 11. The space of principal stresses

下载: 全尺寸图片幻灯片

图 12 ξ与η的关系

Figure 12. Relationship between ξ and stress triaxiality η

下载: 全尺寸图片幻灯片

表 1 混凝土HJC本构模型参数^[20-23]

Table 1. Parameters of the HJC model for cement mortar^[20-23]

ρ₀/(kg·m⁻³)	G/GPa	A	B	C	N	$ f' $/MPa
2 440	14.875	0.69	1.50	0.007	0.61	48

T/MPa	$ {\dot \varepsilon _0}/{{\text{s}}^{ - 1}} $	ε_f,min	S_max	p_c/MPa	μ_c	p_l/MPa
4	1	0.01	7	594.3	0.03	800

μ_l	D₁	D₂	K₁	K₂	K₃
0.1	0.04	1	85	−171	208

下载: 导出CSV

表 2 混凝土DP模型参数

Table 2. Parameters of the DP model for cement mortar

ρ₀/(kg·m⁻³)	E/GPa	ν_con	ϕ/(^o)	k′	ψ/(^o)
2440	35.7	0.3	30	0.78	30

下载: 导出CSV

参考文献(25)

[1]	胡时胜, 王礼立, 宋力, 等. Hopkinson压杆技术在中国的发展回顾 [J]. 爆炸与冲击, 2014, 34(6): 641–657. DOI: 10.11883/1001-1455(2014)06-0641-17. HU S S, WANG L L, SONG L, et al. Review of the development of Hopkinson pressure bar technique in China [J]. Explosion and Shock Waves, 2014, 34(6): 641–657. DOI: 10.11883/1001-1455(2014)06-0641-17.
[2]	徐松林, 单俊芳, 王鹏飞. 脆性材料高应变率压缩失效机制综述与研究进展 [J]. 现代应用物理, 2020, 11(3): 30101. DOI: 10.12061/j.issn.2095-6223.2020.030101. XU S L, SHAN J F, WANG P F. Review and research progress of dynamic failure mechanism for brittle materials under high strain rate [J]. Modern Applied Physics, 2020, 11(3): 30101. DOI: 10.12061/j.issn.2095-6223.2020.030101.
[3]	TANG Z P, XU S L, DAI X Y, et al. S-wave tracing technique to investigate the damage and failure behavior of brittle materials subjected to shock loading [J]. International Journal of Impact Engineering, 2005, 31(9): 1172–1191. DOI: 10.1016/j.ijimpeng.2004.07.005.
[4]	XU S L, HUANG J Y, WANG P F, et al. Investigation of rock material under combined compression and shear dynamic loading: an experimental technique [J]. International Journal of Impact Engineering, 2015, 86: 206–222. DOI: 10.1016/j.ijimpeng.2015.07.014.
[5]	王礼立. 应力波基础 [M]. 2版. 北京: 国防工业出版社, 2005: 29−35.
[6]	王鹏飞, 徐松林, 郑航, 等. 变形模式对多孔金属材料SHPB实验结果的影响 [J]. 力学学报, 2012, 44(5): 928–932. DOI: 10.6052/0459-1879-11-354. WANG P F, XU S L, ZHENG H, et al. Influence of deformation modes on SHPB experimental results of cellular metal [J]. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(5): 928–932. DOI: 10.6052/0459-1879-11-354.
[7]	WANG P F, XU S L, LI Z B, et al. Experimental investigation on the strain-rate effect and inertia effect of closed-cell aluminum foam subjected to dynamic loading [J]. Materials Science and Engineering: A, 2015, 620: 253–261. DOI: 10.1016/j.msea.2014.10.026.
[8]	徐松林, 王鹏飞, 赵坚, 等. 基于三维Hopkinson杆的混凝土动态力学性能研究 [J]. 爆炸与冲击, 2017, 37(2): 180–185. DOI: 10.11883/1001-1455(2017)02-0180-06. XU S L, WANG P F, ZHAO J, et al. Dynamic behavior of concrete under static triaxial loading using 3D-Hopkinson bar [J]. Explosion and Shock Waves, 2017, 37(2): 180–185. DOI: 10.11883/1001-1455(2017)02-0180-06.
[9]	徐松林, 王鹏飞, 单俊芳, 等. 真三轴静载作用下混凝土的动态力学性能研究 [J]. 振动与冲击, 2018, 37(15): 59–67. DOI: 10.13465/j.cnki.jvs.2018.15.008. XU S L, WANG P F, SHAN J F, et al. Dynamic behavior of concrete under static tri-axial loadings [J]. Journal of Vibration and Shock, 2018, 37(15): 59–67. DOI: 10.13465/j.cnki.jvs.2018.15.008.
[10]	XU S L, SHAN J F, ZHANG L, et al. Dynamic compression behaviors of concrete under true triaxial confinement: an experimental technique [J]. Mechanics of Materials, 2020, 140: 103220. DOI: 10.1016/j.mechmat.2019.103220.
[11]	GROTE D L, PARK S W, ZHOU M. Dynamic behavior of concrete at high strain rates and pressures: Ⅰ: experimental characterization [J]. International Journal of Impact Engineering, 2001, 25(9): 869–886. DOI: 10.1016/S0734-743X(01)00020-3.
[12]	高光发. 混凝土材料动态压缩强度的应变率强化规律 [J]. 高压物理学报, 2017, 31(3): 261–270. DOI: 10.11858/gywlxb.2017.03.007. GAO G F. Effect of strain-rate hardening on dynamic compressive strength of plain concrete [J]. Chinese Journal of High Pressure Physics, 2017, 31(3): 261–270. DOI: 10.11858/gywlxb.2017.03.007.
[13]	LI Q M, MENG H. About the dynamic strength enhancement of concrete-like materials in a split Hopkinson pressure bar test [J]. International Journal of Solids and Structures, 2003, 40(2): 343–360. DOI: 10.1016/S0020-7683(02)00526-7.
[14]	MENG H, LI Q M. Correlation between the accuracy of a SHPB test and the stress uniformity based on numerical experiments [J]. International Journal of Impact Engineering, 2003, 28(5): 537–555. DOI: 10.1016/S0734-743X(02)00073-8.
[15]	MENG H, LI Q M. Modification of SHPB set-up to minimize wave dispersion and attenuation effects [J]. International Journal of Impact Engineering, 2003, 28(6): 677–696. DOI: 10.1016/S0734-743X(02)00124-0.
[16]	LI Q M, LU Y B, MENG H. Further investigation on the dynamic compressive strength enhancement of concrete-like materials based on split Hopkinson pressure bar tests: Part Ⅱ: numerical simulations [J]. International Journal of Impact Engineering, 2009, 36(12): 1335–1345. DOI: 10.1016/j.ijimpeng.2009.04.010.
[17]	杨茨, 徐松林, 易洪昇. 冲击载荷下圆环压缩变形特性研究 [J]. 振动与冲击, 2015, 34(11): 128–132,145. DOI: 10.13465/j.cnki.jvs.2015.11.023. YANG C, XU S L, YI H S. Deformation properties of a ring under impact loading [J]. Chinese Journal of Vibration and Shock, 2015, 34(11): 128–132,145. DOI: 10.13465/j.cnki.jvs.2015.11.023.
[18]	FORRESTAL M J, WRIGHT T W, CHEN W. The effect of radial inertia on brittle samples during the split Hopkinson pressure bar test [J]. International Journal of Impact Engineering, 2007, 34(3): 405–411. DOI: 10.1016/j.ijimpeng.2005.12.001.
[19]	FORQUIN P, GARY G, GATUINGT F. A testing technique for concrete under confinement at high rates of strain [J]. International Journal of Impact Engineering, 2008, 35(6): 425–446. DOI: 10.1016/j.ijimpeng.2007.04.007.
[20]	HOLMQUIST T J, JOHNSON G R. A computational constitutive model for concrete subjected to larger strains, high strain rates and high pressure [C]//JACKSON N, DICKERT S. 14th International Symposium on Ballistics. USA: American Defense Preparedness Association, 1995: 591−600.
[21]	BAILLY P, DELVARE F, VIAL J, et al. Dynamic behavior of an aggregate material at simultaneous high pressure and strain rate: SHPB triaxial tests [J]. International Journal of Impact Engineering, 2011, 38(2/3): 73–84. DOI: 10.1016/j.ijimpeng.2010.10.005.
[22]	ALEJANO L R, BOBET A. Drucker-prager criterion [J]. Rock Mechanics and Rock Engineering, 2012, 45(6): 995–999. DOI: 10.1007/s00603-012-0278-2.
[23]	苗春贺, 陈丽娜, 单俊芳, 等. 水泥砂浆抗弹性能研究 [J]. 高压物理学报, 2021, 35(2): 024205. DOI: 10.11858/gywlxb.20200609. MIAO C H, CHEN L N, SHAN J F, et al. Research on the ballistic performance of cement mortar [J]. Chinese Journal of High Pressure Physics, 2021, 35(2): 024205. DOI: 10.11858/gywlxb.20200609.
[24]	刘孝敏, 胡时胜. 大直径SHPB弥散效应的二维数值分析 [J]. 实验力学, 2000, 15(4): 371–376. DOI: 10.3969/j.issn.1001-4888.2000.04.003. LIU X M, HU S S. Two-dimensional numerical analysis for the dispersion of stress waves in large-diameter-SHPB [J]. Journal of Experimental Mechanics, 2000, 15(4): 371–376. DOI: 10.3969/j.issn.1001-4888.2000.04.003.
[25]	BAI Y L, TENG X Q, WIERZBICKI T. On the application of stress triaxiality formula for plane strain fracture testing [J]. Journal of Engineering Materials and Technology, 2009, 131(2): 021002. DOI: 10.1115/1.3078390.