基于Ottosen屈服条件的不同强度混凝土空腔膨胀模型及侵彻机理

张雪岩; 孙凯; 李元龙; 曾费隐; 李国杰; 武海军

doi:10.11883/bzycj-2022-0511

基于Ottosen屈服条件的不同强度混凝土空腔膨胀模型及侵彻机理

doi: 10.11883/bzycj-2022-0511

张雪岩^{1, 2,},
孙凯¹,
李元龙¹,
曾费隐¹,
李国杰¹,
武海军^2, ,

1.
北京航天长征飞行器研究所，北京 100076
2.
北京理工大学爆炸科学与技术国家重点实验室，北京 100081

基金项目: 国家自然科学基金（11572048, 11390362）

详细信息

作者简介:
张雪岩（1992－　），男，博士，工程师，zxy_Maple@163.com

通讯作者:
武海军（1974－　），男，博士，教授，博士生导师，wuhjbit@bit.edu.cn

中图分类号: O383; TU528.01
计量
- 文章访问数: 260
- HTML全文浏览量: 51
- PDF下载量: 69
- 被引次数: 0
出版历程
- 收稿日期: 2022-11-14
- 修回日期: 2023-08-24
- 网络出版日期: 2023-08-28
- 刊出日期: 2023-09-11

Cavity expansion model and penetration mechanism of concrete with different strengths based on the Ottosen yield condition

ZHANG Xueyan^{1, 2
,},
SUN Kai¹,
LI Yuanlong¹,
ZENG Feiyin¹,
LI Guojie¹,
WU Haijun^{2
, ,}

1.
Beijing Aerospace Long March Aircraft Research Institute, Beijing 100076, China
2.
State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China

摘要

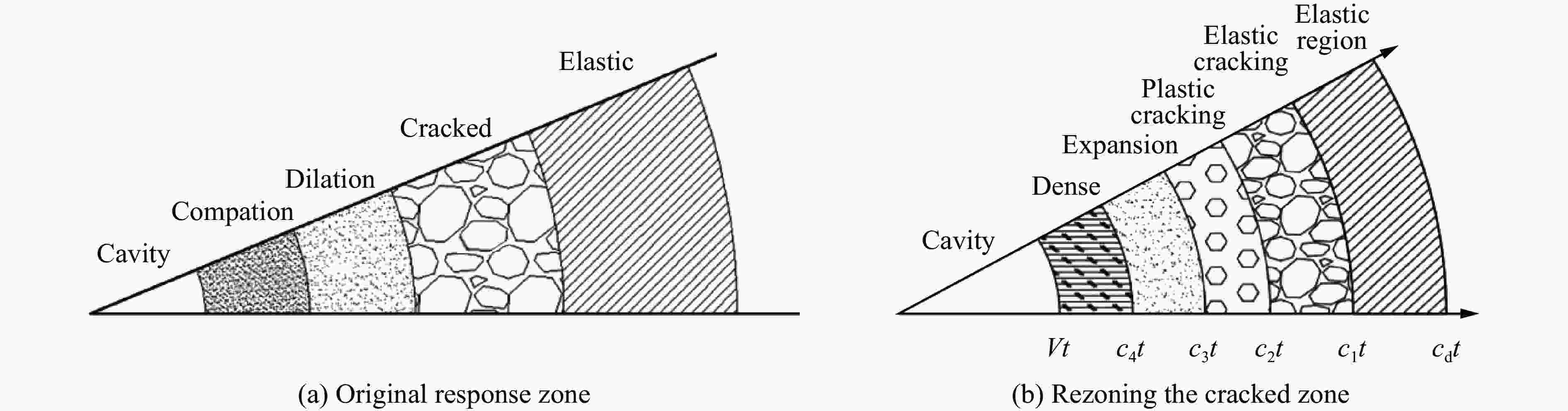
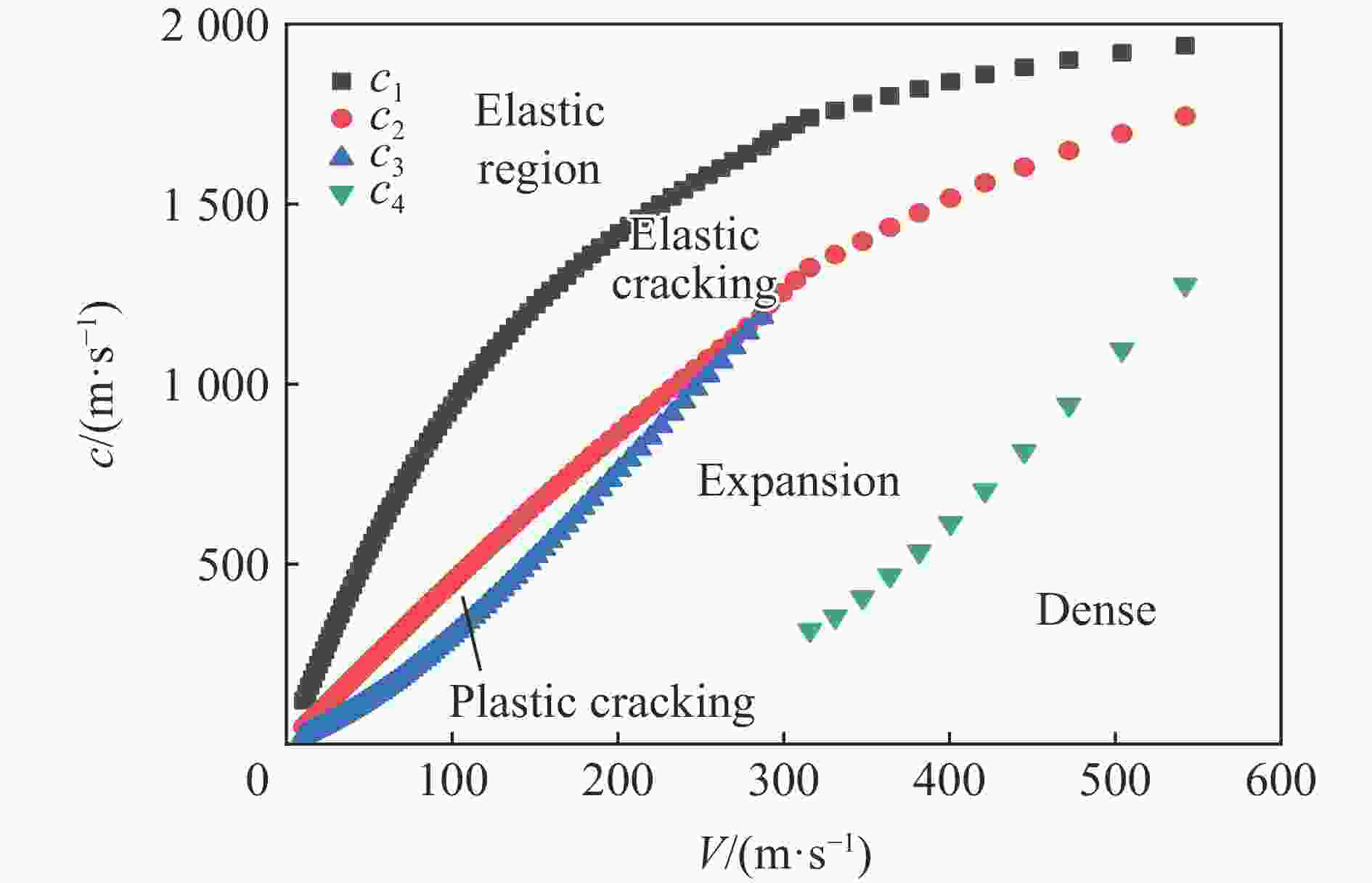
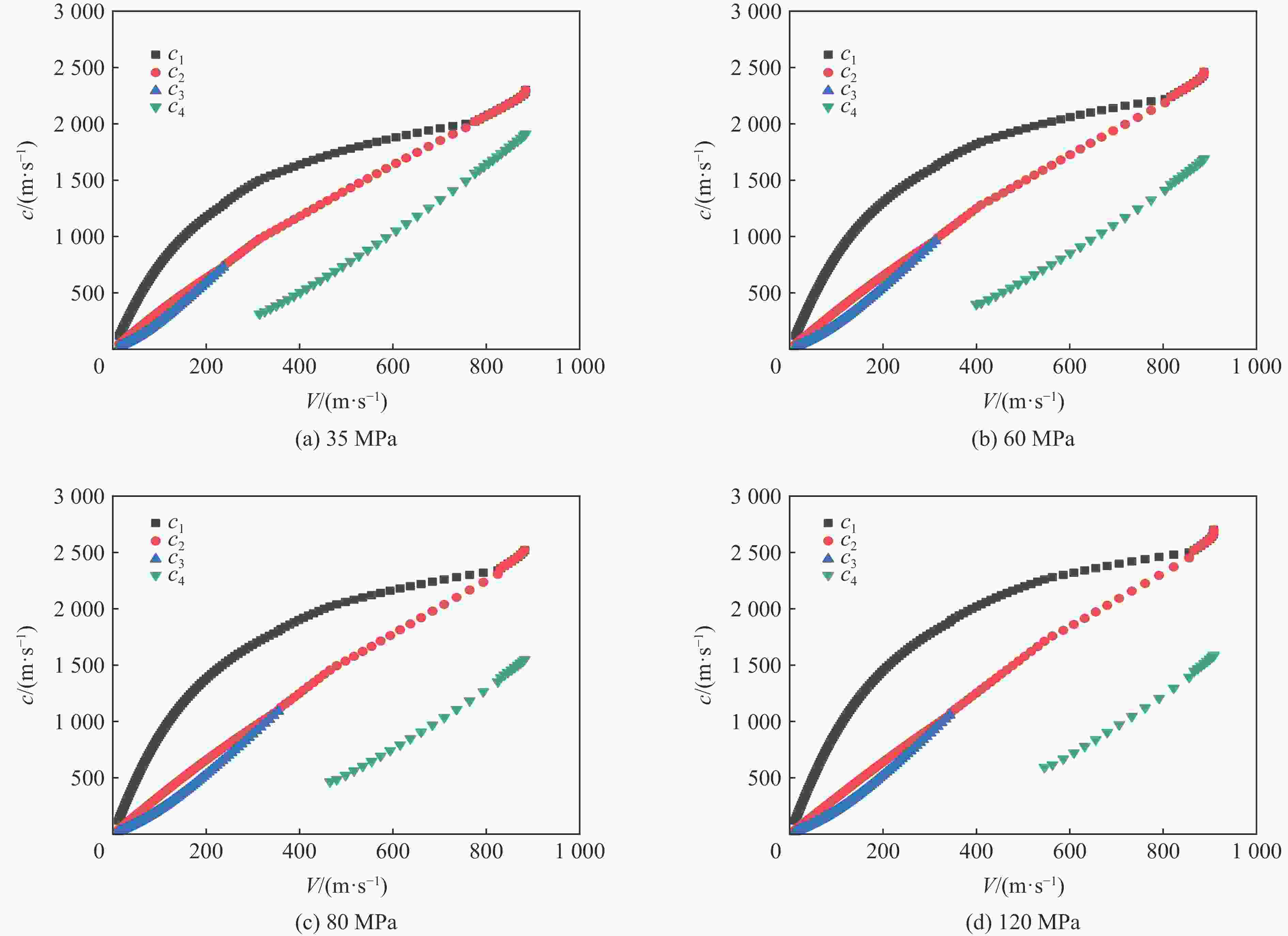
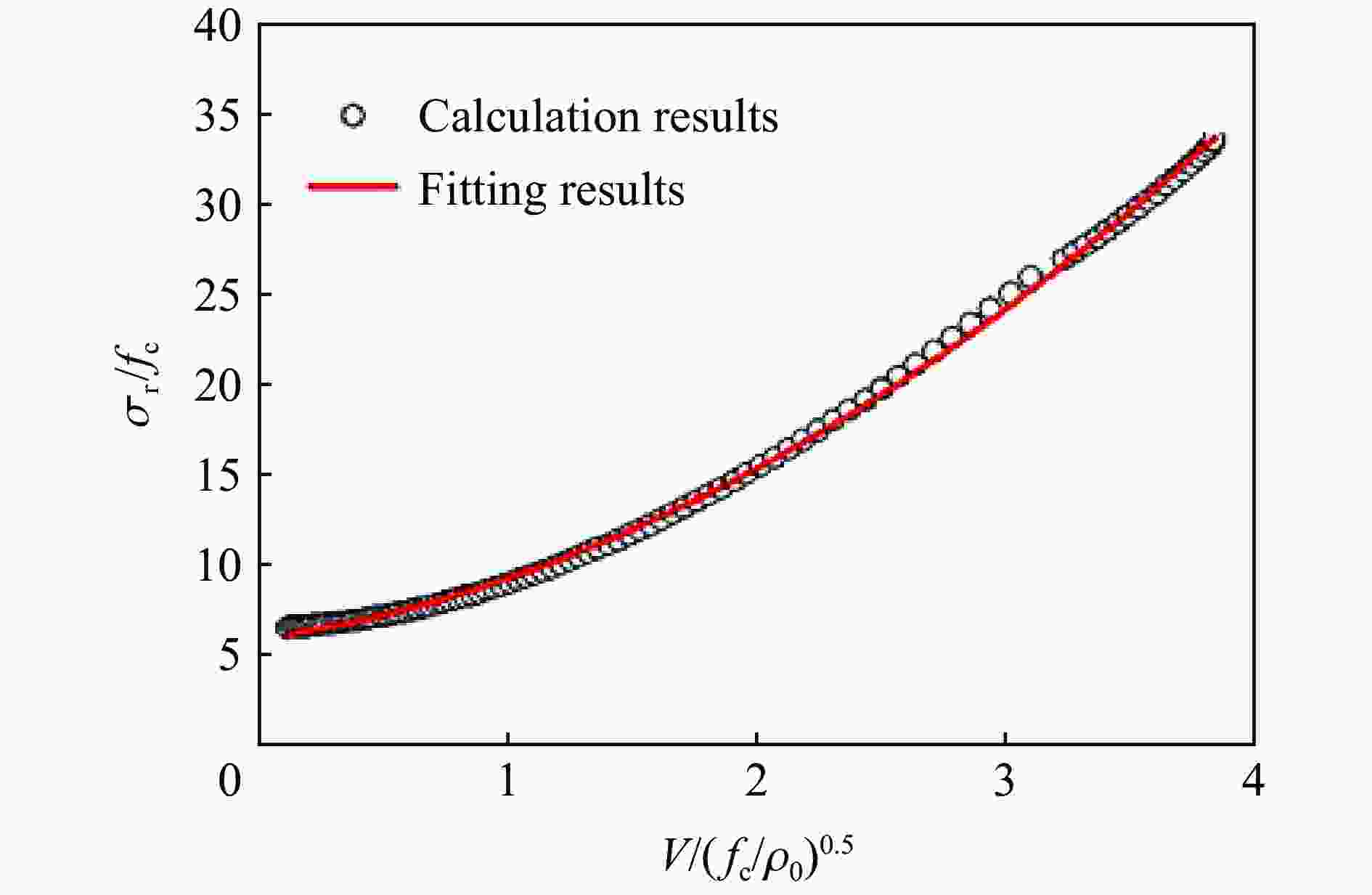
摘要: 针对毁伤与防护领域对深层超硬目标理论研究及工程应用的迫切需求，引入改进的Ottosen屈服条件，对混凝土空腔膨胀过程中的响应分区和边界条件进行优化，求解空腔膨胀的全过程，分析不同强度混凝土响应分区的变化规律；根据空腔边界应力和空腔膨胀速度的关系，建立了弹体侵彻深度计算模型，对弹体侵彻不同强度混凝土工况进行了对比计算，并深入分析了靶体强度对侵彻深度影响的机理。通过与实验数据进行对比发现，改进的空腔膨胀理论对于普通混凝土和高强混凝土均有很好的适用性，可准确计算径向应力与空腔边界速度关系以及侵彻深度。研究结果显示，高强混凝土的弹塑性开裂区范围更大，密实区范围更小，表明了高强混凝土脆性大，材质密实的特点，引入塑性开裂区可以更好地反应侵彻过程中高强混凝土压实时对应速度更高的现象；随着混凝土强度的提高，其屈服包络面变化越来越小，因此混凝土的空腔边界应力增大但变化程度越来越小，导致弹体侵彻深度随速度增加的增量变小。
- Ottosen屈服条件 /
- 空腔膨胀理论 /
- 高强混凝土 /
- 侵彻深度
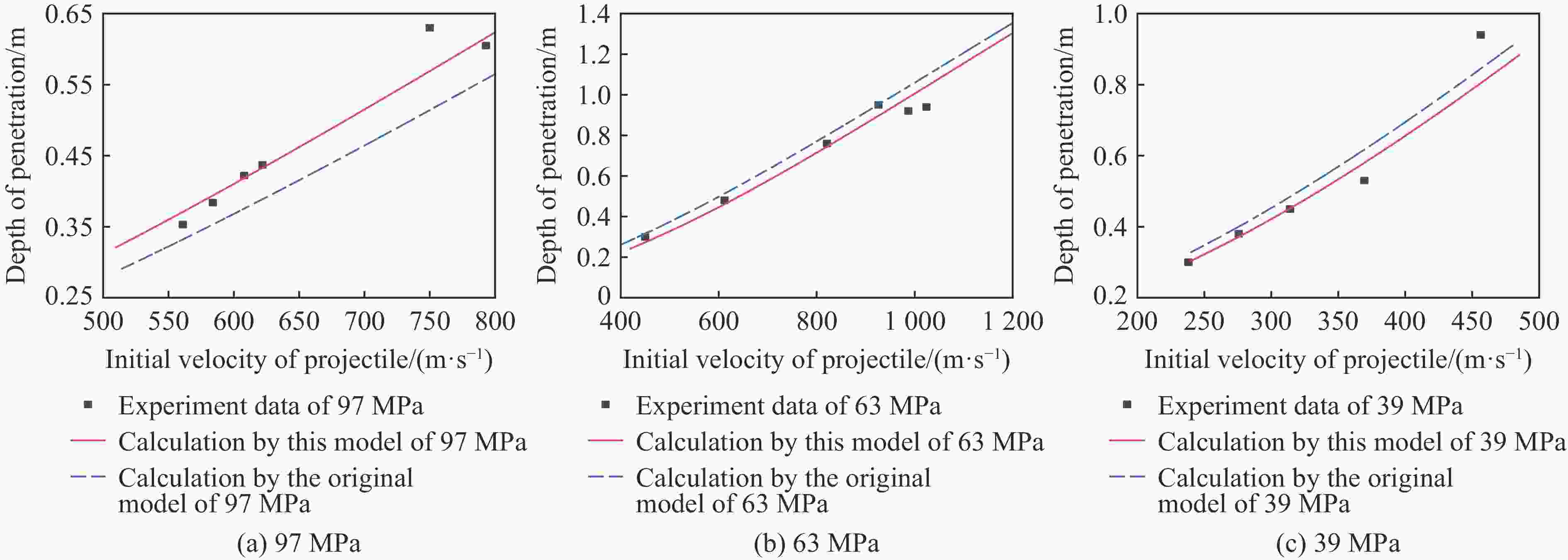
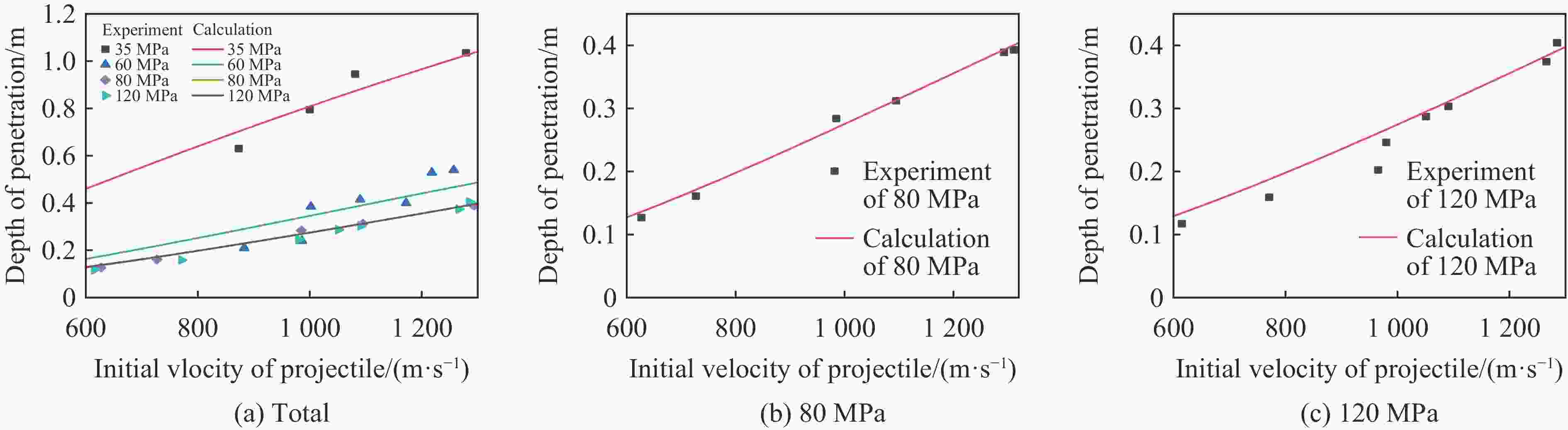
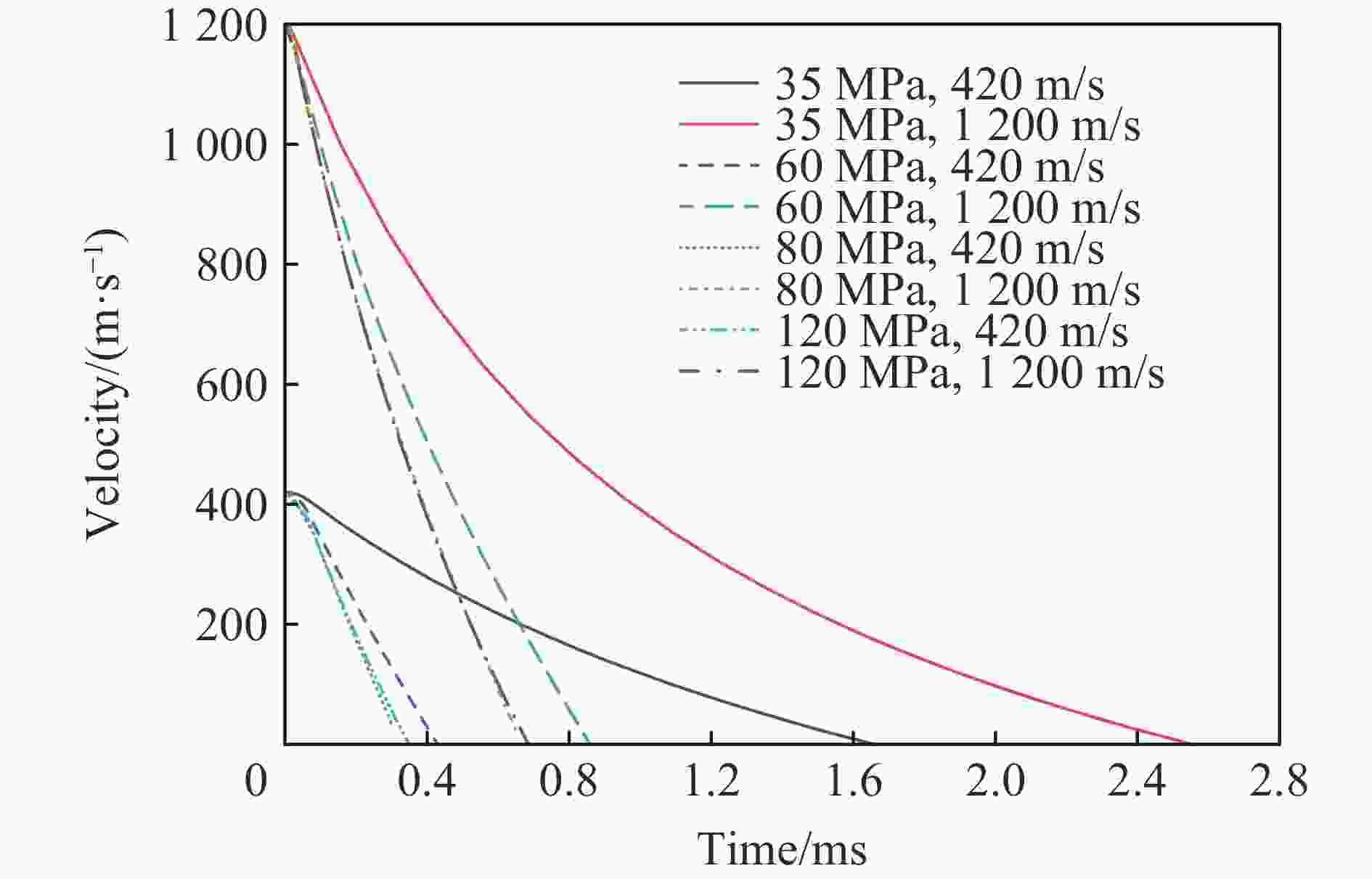
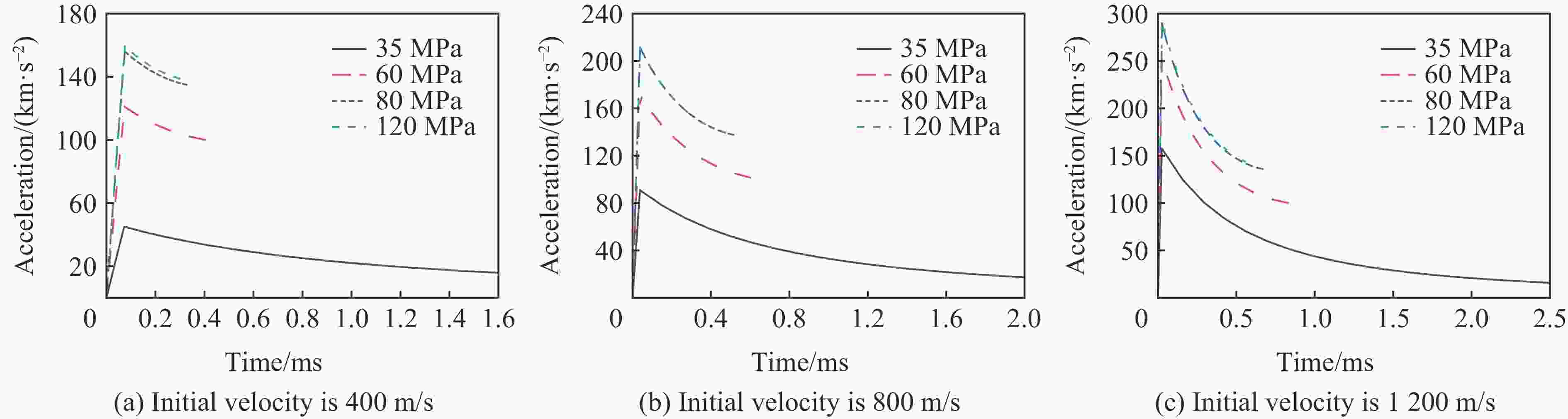
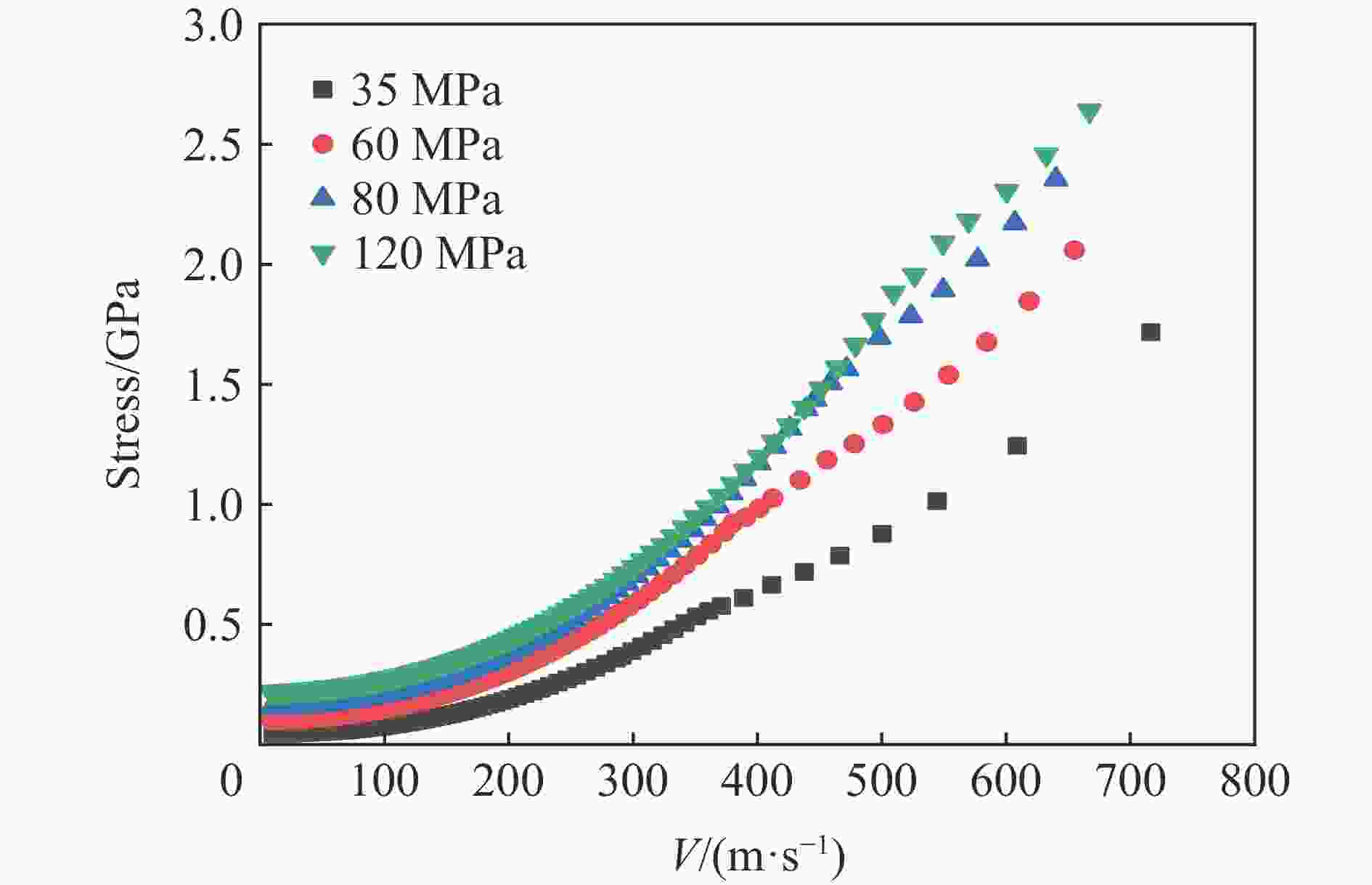
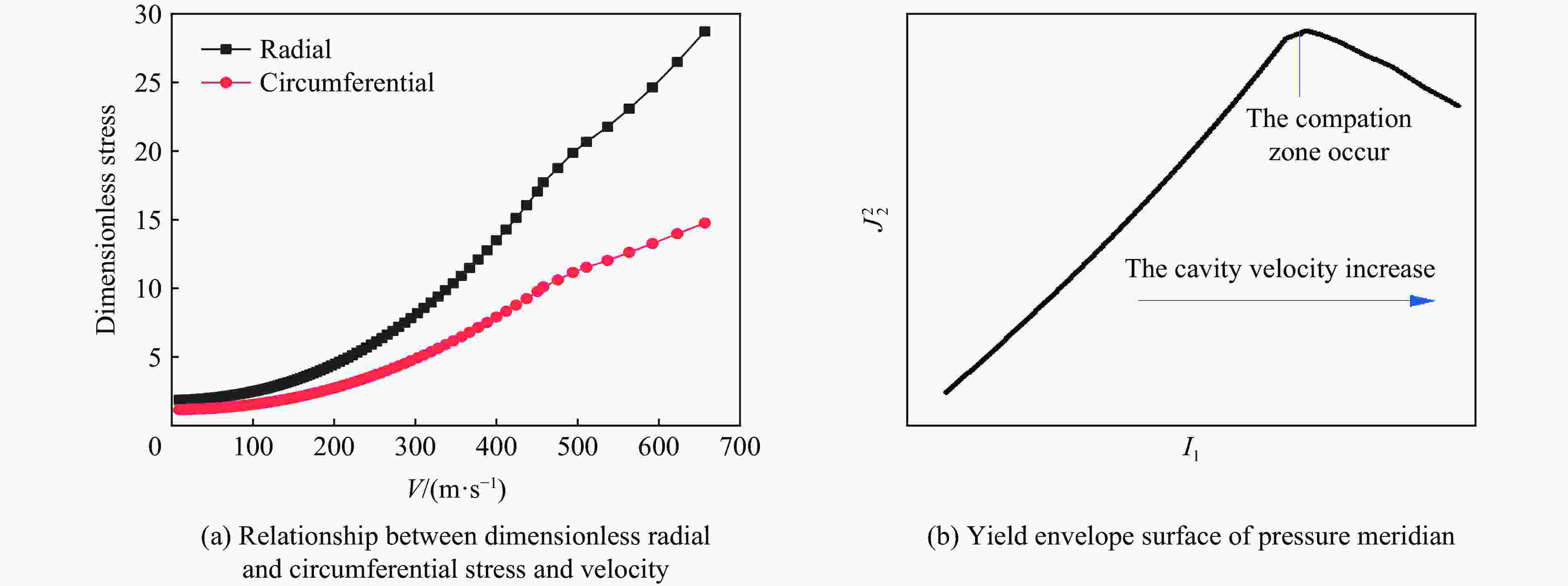
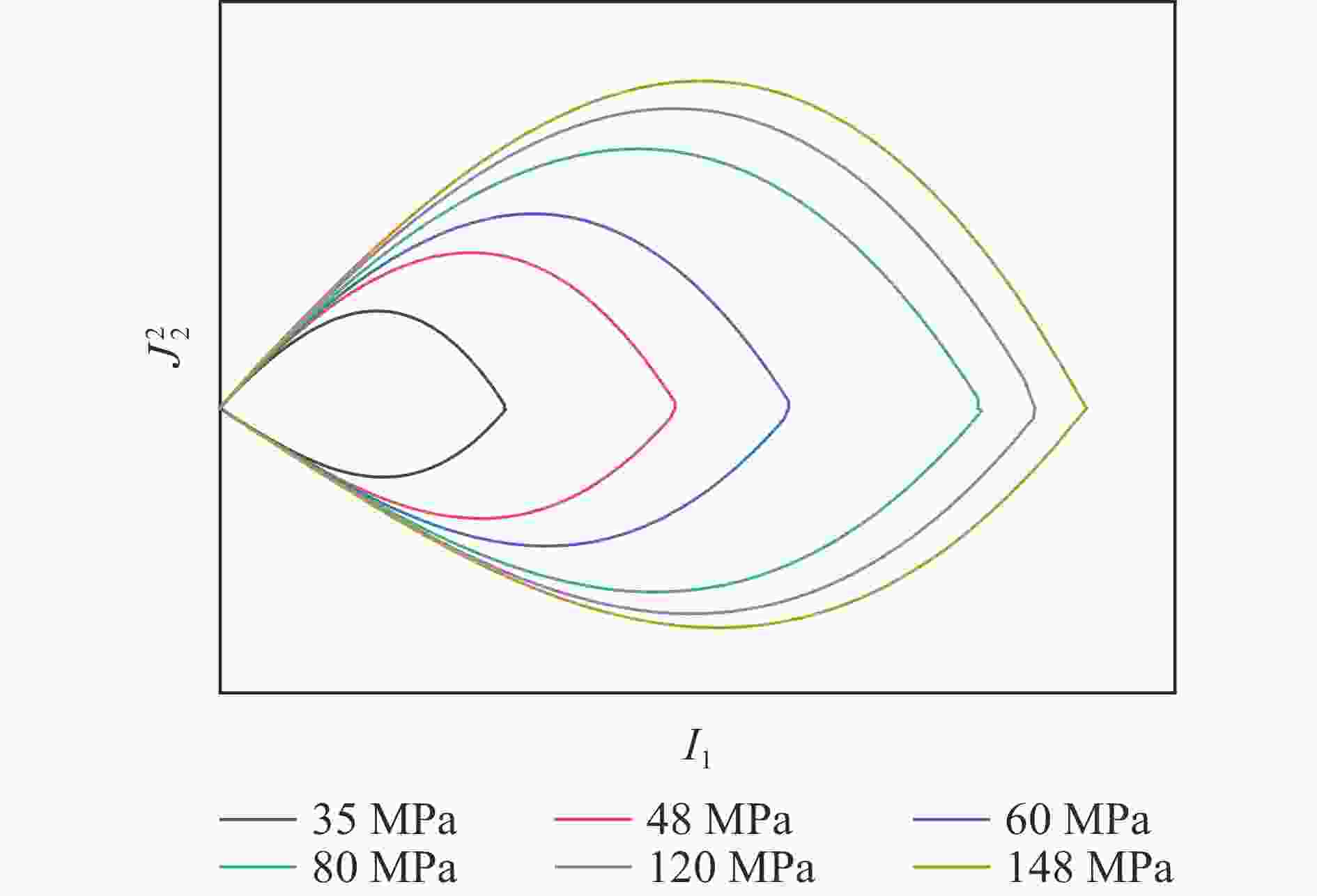
Abstract: Aiming at the urgent demand for theoretical research and engineering application of deep super hard targets in the field of damage and protection, the response zone and boundary conditions during the cavity expansding process are optimized in this paper based on the improved Ottosen yield condition. The entire process of cavity expansion is solved, the changes in the response zone of concrete with different strengths are analyzed. According to the relationship between cavity boundary stress and cavity expansion velocity, a calculation model of projectile penetration depth is established, and the penetration depth of projectile penetration into concrete with different strengths are calculated. The mechanism of the influence of target strength on penetration depth is also analyzed. The results show that the elastic and plastic cracking zone of high-strength concrete is larger and the compacted zone is smaller, indicating that high-strength concrete is more brittle and compact. And the addition of plastic cracking zone can better reflect the phenomenon of concrete with different strengths in penetration. By comparing with the experimental data, it can be seen that the cavity expansion theory established in this paper has good applicability for normal concrete and high-strength concrete. The relationship between radial stress and cavity boundary velocity and the penetration depth also can be accurately calculated by this theory. With the increase of concrete strength, the difference in the cavity boundary stress of the concrete becomes smaller, resulting in a smaller increase in the penetration depth of the projectile as the velocity increases, and the penetration depth of the projectile decreases and gradually tends to a certain value at the same speed.
- Ottosen yield condition /
- cavity expansion theory /
- high-strength concrete /
- depth of penetration

HTML全文

图 1 不同屈服条件偏平面形状

Figure 1. Partial plane shapes with different yield conditions

下载: 全尺寸图片幻灯片

图 2 空腔膨胀理论响应分区

Figure 2. Response zone of cavity expansion theory

下载: 全尺寸图片幻灯片

图 3 响应区界面传播速度与空腔边界膨胀速度关系

Figure 3. Relationship between the interface propagation velocity in response zone and thecavity boundary expansion velocity

下载: 全尺寸图片幻灯片

图 4 不同强度混凝土响应区域界面传播速度与空腔边界膨胀速度关系

Figure 4. Relationship between interface propagation velocity in response zone and cavity boundaryexpansion velocity of different strength concrete

下载: 全尺寸图片幻灯片

图 5 不考虑塑性开裂区时不同强度混凝土的响应区域界面传播速度

Figure 5. Interface propagation velocity in response zone of different strength concrete without considering plastic cracking zone

下载: 全尺寸图片幻灯片

图 6 无量纲空腔边界径向应力与空腔边界膨胀速度关系

Figure 6. The relationship between the dimensionless radialstress of the cavity boundary and the expansionvelocity of the cavity boundary

下载: 全尺寸图片幻灯片

图 7 任意头部弹体的受力分析

Figure 7. Force analysis of projectile with arbitrary head

下载: 全尺寸图片幻灯片

图 8 弹体侵彻不同强度混凝土实验结果与计算结果对比

Figure 8. Experimental and calculated results for the projectile penetrating concrete with different strength

下载: 全尺寸图片幻灯片

图 9 弹体侵彻不同强度混凝土实验结果与计算结果对比

Figure 9. Comparison of experimental and calculated results of projectile penetration into concrete with different strengths

下载: 全尺寸图片幻灯片

图 10 弹体侵彻不同强度混凝土速度-时间曲线对比

Figure 10. Comparison of speed-time curves of projectile penetration into concrete with different strengths

下载: 全尺寸图片幻灯片

图 11 弹体侵彻不同强度混凝土的加速度-时间曲线

Figure 11. Deceleration-time curve of projectile penetration into concrete with different strength

下载: 全尺寸图片幻灯片

图 12 空腔边界应力与速度关系

Figure 12. Relationship between stress of cavityboundary and velocity

下载: 全尺寸图片幻灯片

图 13 80 MPa混凝土应力状态示意

Figure 13. Schematic diagram of the stress state of 80 MPa concrete

下载: 全尺寸图片幻灯片

图 14 不同强度混凝土的屈服包络面

Figure 14. Yield envelope surface of different strength concrete

下载: 全尺寸图片幻灯片

表 1 不同抗压强度混凝土的力学性能参数

Table 1. Mechanical properties of concrete with different compressive strength

抗压强度/MPa	密度/（kg·m⁻³）	弹性模量/GPa	泊松比	拉压比	屈服强度/MPa	扩容时强度/MPa
35	2380	28.8	0.2	0.076	8.8	33.7
60	2420	33.9	0.2	0.062	15.6	58.9
80	2450	36.9	0.2	0.055	22.7	78.7
120	2500	41.7	0.2	0.047	35.1	114.6
注：数据来自于文献[20-21]和基于改进的Ottosen屈服条件计算得到。

下载: 导出CSV

表 2 不同强度混凝土的力学性能参数

Table 2. Mechanical property parameters of concrete with different strengths

抗压强度/MPa	密度/（kg·m⁻³）	弹性模量/GPa	泊松比	拉压比	屈服强度/MPa	扩容时强度/MPa
39	2400	29.2	0.2	0.075	9.2	37.3
63	2420	34.8	0.2	0.061	18.6	60.9
97	2520	39.8	0.2	0.049	29.7	94.8

下载: 导出CSV

参考文献(35)

[1]	FORRESTAL M J, TZOU D Y. A spherical cavity-expansion penetration model for concrete targets [J]. International Journal of Solids and Structures, 1997, 34(31/32): 4127–4146. DOI: 10.1016/S0020-7683(97)00017-6.
[2]	FORRESTAL M J, LUK V K. Dynamic spherical cavity-expansion in a compressible elastic-plastic solid [J]. Journal of Applied Mechanics, 1988, 55(2): 275–279. DOI: 10.1115/1.3173672.
[3]	黄民荣, 顾晓辉, 高永宏. 脆性材料静态抗侵彻阻力简化计算模型与对比研究 [J]. 弹道学报, 2009, 21(2): 86–89. HUANG M R, GU X H, GAO Y H. Simplified analytical model and its contrast study on the static penetration resistance of brittle materials [J]. Journal of Ballistics, 2009, 21(2): 86–89.
[4]	黄民荣, 顾晓辉, 高永宏. 基于Griffith强度理论的空腔膨胀模型与应用研究 [J]. 力学与实践, 2009, 31(5): 30–34. DOI: 10.6052/1000-0879-2008-351. HUANG M R, GU X H, GAO Y H. Cavity expansion model based on the Griffith strength theory and its application [J]. Mechanics in Engineering, 2009, 31(5): 30–34. DOI: 10.6052/1000-0879-2008-351.
[5]	ZHANG S, WU H J, TAN Z J, et al. Theoretical analysis of dynamic spherical cavity expansion in reinforced concretes [J]. Key Engineering Materials, 2016, 715: 222–227. DOI: 10.4028/www.scientific.net/KEM.715.222.
[6]	曹扬悦也, 蒋志刚, 谭清华, 等. 基于Hoek-Brown准则的混凝土-岩石类靶侵彻模型 [J]. 振动与冲击, 2017, 36(5): 48–53, 60. DOI: 10.13465/j.cnki.jvs.2017.05.008. CAO Y Y Y, JIANG Z G, TAN Q H, et al. Penetration model for concrete-rock targets based on Hoek-Brown criterion [J]. Journal of Vibration and Shock, 2017, 36(5): 48–53, 60. DOI: 10.13465/j.cnki.jvs.2017.05.008.
[7]	詹昊雯, 曹扬悦也, 蒋志刚, 等. 约束混凝土靶的准静态柱形空腔膨胀理论 [J]. 弹道学报, 2017, 29(2): 13–18. ZHAN H W, CAO Y Y Y, JIANG Z G, et al. Quasi-static cylindrical cavity-expansion model for confined-concrete targets [J]. Journal of Ballistics, 2017, 29(2): 13–18.
[8]	XU H, WEN H M. A spherical cavity expansion penetration model for concrete based on Hoek-Brown strength criterion [J]. International Journal of Nonlinear Sciences and Numerical Simulation, 2012, 13(2): 145–152. DOI: 10.1515/ijnsns-2011-099.
[9]	FENG J, LI W B, WANG X M, et al. Dynamic spherical cavity expansion analysis of rate-dependent concrete material with scale effect [J]. International Journal of Impact Engineering, 2015, 84: 24–37. DOI: 10.1016/j.ijimpeng.2015.05.005.
[10]	SATAPATHY S. Dynamic spherical cavity expansion in brittle ceramics [J]. International Journal of Solids and Structures, 2001, 38(32/33): 5833–5845. DOI: 10.1016/S0020-7683(00)00388-7.
[11]	李志康, 黄风雷. 高速长杆弹侵彻半无限混凝土靶的理论分析 [J]. 北京理工大学学报, 2010, 30(1): 10–13. DOI: 10.15918/j.tbit1001-0645.2010.01.002. LI Z K, HUANG F L. High velocity long rod projectile’s penetration into semi-infinite concrete targets [J]. Transactions of Beijing Institute of Technology, 2010, 30(1): 10–13. DOI: 10.15918/j.tbit1001-0645.2010.01.002.
[12]	李志康. 弹体正侵彻半无限混凝土靶的理论分析 [D]. 北京: 北京理工大学, 2008.
[13]	王一楠. 动能弹体高速侵彻混凝土机理研究 [D]. 北京: 北京理工大学, 2009.
[14]	何涛. 动能弹在不同材料靶体中的侵彻行为研究 [D]. 合肥: 中国科学技术大学, 2007. HE T. A study on the penetration of projectiles into targets made of various materials [D]. Hefei: University of Science and Technology of China, 2007.
[15]	HE T, WEN H M, GUO X J. A spherical cavity expansion model for penetration of ogival-nosed projectiles into concrete targets with shear-dilatancy [J]. Acta Mechanica Sinica, 2011, 27(6): 1001–1012. DOI: 10.1007/s10409-011-0505-1.
[16]	张欣欣, 闫雷, 武海军, 等. 考虑剪胀效应的混凝土动态球形空腔膨胀理论 [J]. 兵工学报, 2016, 37(1): 42–49. DOI: 10.3969/j.issn.1000-1093.2016.01.007. ZHANG X X, YAN L, WU H J, et al. A note on the dynamic spherical cavity expansion of concrete with shear dilatancy [J]. Acta Armamentarii, 2016, 37(1): 42–49. DOI: 10.3969/j.issn.1000-1093.2016.01.007.
[17]	ZHANG X Y, WU H J, LI J Z, et al. A constitutive model of concrete based on Ottosen yield criterion [J]. International Journal of Solids and Structures, 2020, 193/194: 79–89. DOI: 10.1016/j.ijsolstr.2020.02.013.
[18]	OTTOSEN N S. A failure criterion for concrete [J]. Journal of Engineering Mechanics Division, 1997, 103(4): 527–535.
[19]	过镇海. 混凝土的强度和变形-试验基础和本构关系 [M]. 北京: 清华大学出版社, 1997.
[20]	ČERVENKA J, PAPANIKOLAOU V K. Three dimensional combined fracture-plastic material model for concrete [J]. International Journal of Plasticity, 2008, 24(12): 2192–2220. DOI: 10.1016/j.ijplas.2008.01.004.
[21]	PAPANIKOLAOU V K, KAPPOS A J. Confinement-sensitive plasticity constitutive model for concrete in triaxial compression [J]. International Journal of Solids and Structures, 2007, 44(21): 7021–7048. DOI: 10.1016/j.ijsolstr.2007.03.022.
[22]	ARÁOZ G, LUCCIONI B. Modeling concrete like materials under sever dynamic pressures [J]. International Journal of Impact Engineering, 2015, 76: 139–154. DOI: 10.1016/j.ijimpeng.2014.09.009.
[23]	DAHL K K B. A constitutive model for normal and high strength concrete [R]. Anker Engelunds Vej: Technical University of Denmark, 1992.
[24]	KUPFER H, HILSDORF K H, RUSH H. Behavior of concrete under biaxial stresses [J]. Journal of the Engineering Mechanics Division Asce, 1969, 99(8): 656–666. DOI: 10.14359/7388.
[25]	IMRAN I, PANTAZOPOULOU S J. Plasticity model for concrete under triaxial compression[J]. Journal of Engineering Mechanics, 2001, 127(3): 281–290. DOI: 10.1061/(ASCE)0733-9399(2001)127:3(281).
[26]	GABET T, MALÉCOT Y, DAUDEVILLE L. Triaxial behaviour of concrete under high stresses: influence of the loading path on compaction and limit states [J]. Cement and Concrete Research, 2008, 38(3): 403–412. DOI: 10.1016/j.cemconres.2007.09.029.
[27]	VU X H, MALECOT Y, DAUDEVILLE L, et al. Experimental analysis of concrete behavior under high confinement: Effect of the saturation ratio [J]. International Journal of Solids and Structures, 2009, 46(5): 1105–1120. DOI: 10.1016/j.ijsolstr.2008.10.015.
[28]	FORRESTAL M J, ALTMAN B S, CARGILE J D, et al. An empirical equation for penetration depth of ogive-nose projectiles into concrete targets [J]. International Journal of Impact Engineering, 1994, 15(4): 395–405. DOI: 10.1016/0734-743X(94)80024-4.
[29]	FORRESTAL M J, FREW D J, HANCHAK S J, et al. Penetration of grout and concrete targets with ogive-nose steel projectiles [J]. International Journal of Impact Engineering, 1996, 18(5): 465–476. DOI: 10.1016/0734-743X(95)00048-F.
[30]	FORRESTAL M J, FREW D J, HICKERSON J P, et al. Penetration of concrete targets with deceleration-time measurements [J]. International Journal of Impact Engineering, 2003, 28(5): 479–497. DOI: 10.1016/S0734-743X(02)00108-2.
[31]	武海军, 黄风雷, 王一楠, 等. 高速侵彻混凝土弹体头部侵蚀终点效应实验研究 [J]. 兵工学报, 2012, 33(1): 48–55. WU H J, HUANG F L, WANG Y N, et al. Experimental investigation on projectile nose eroding effect of high-velocity penetration into concrete [J]. Acta Armamentarii, 2012, 33(1): 48–55.
[32]	张雪岩, 武海军, 李金柱, 等. 弹体高速侵彻两种强度混凝土靶的对比研究 [J]. 兵工学报, 2019, 40(2): 276–283. DOI: 10.3969/j.issn.1000-1093.2019.02.007. ZHANG X Y, WU H J, LI J Z, et al. Comparative study of projectiles penetrating into two kinds of concrete targets at high velocity [J]. Acta Armamentarii, 2019, 40(2): 276–283. DOI: 10.3969/j.issn.1000-1093.2019.02.007.
[33]	WU H, FANG Q, CHEN X W, et al. Projectile penetration of ultra-high performance cement based composites at 510-1320m/s [J]. Construction and Building Materials, 2015, 74: 188–200. DOI: 10.1016/j.conbuildmat.2014.10.041.
[34]	吴昊, 方秦, 龚自明. HSFRC靶体的弹体侵彻试验与理论分析 [J]. 弹道学报, 2012, 24(3): 19–24, 53. DOI: 10.3969/j.issn.1004-499X.2012.03.005. WU H, FANG Q, GONG Z M. Experiments and theoretical analyses on HSFRC target under the impact of rigid projectile [J]. Journal of Ballistics, 2012, 24(3): 19–24, 53. DOI: 10.3969/j.issn.1004-499X.2012.03.005.
[35]	ZHANG M H, SHIM V P W, LU G, et al. Resistance of high-strength concrete to projectile impact [J]. International Journal of Impact Engineering, 2005, 31(7): 825–841. DOI: 10.1016/j.ijimpeng.2004.04.009.