薄壁椭球壳在冲击载荷作用下的动态变形模型

范升阳; 栗建桥

doi:10.11883/bzycj-2024-0062

薄壁椭球壳在冲击载荷作用下的动态变形模型

doi: 10.11883/bzycj-2024-0062

范升阳,
栗建桥^,

北京理工大学爆炸科学与安全防护全国重点实验室，北京 100081

基金项目: 国家自然科学基金面上项目（12172054）

详细信息

作者简介:
范升阳（1999－　），男，硕士研究生，531540772@qq.com

通讯作者:
栗建桥（1987－　），男，博士，特别副研究员，jqli@bit.edu.cn

中图分类号: O347
计量
- 文章访问数: 136
- HTML全文浏览量: 18
- PDF下载量: 39
- 被引次数: 0
出版历程
- 收稿日期: 2024-03-06
- 修回日期: 2024-12-22
- 网络出版日期: 2024-12-25

Dynamic deformation model of thin-walled ellipsoidal shells under impact loading

FAN Shengyang,
LI Jianqiao^,

State Key Laboratory of Explosion Science and Safety Protection, Beijing Institute of Technology, Beijing 100081, China

摘要

摘要: 为探究薄壁椭球壳在局部冲击载荷作用下的变形特征，开展了实验和数值模拟研究。利用轻气枪开展弹丸冲击实验，采用三维数字图像相关技术记录变形过程，得到了圆柱弹丸以不同初始冲击速度作用下椭球壳的全局变形形貌以及中心凹陷深度和凹陷边界。在弹丸冲击椭球壳的数值模拟中，重点研究了3种曲率半径变化对椭球壳凹陷深度、凹陷长短轴的影响规律，通过量纲分析方法得出了无量纲变形特征所依赖的主要无量纲自变量，通过参数敏感性分析消减影响较小的参数，在保持相同材料、弹体尺寸与壳体厚度同一缩比时，得到了无量纲变形特征与3种曲率半径和速度之间的响应面函数表达式，并提出了根据凹陷深度、凹陷边界预测全局变形的公式，所得表达式尺寸效应良好，预测精度较高，可为工程中大尺寸曲面薄壳冲击载荷防护设计提供参考。
- 薄壁椭球壳 /
- 冲击载荷 /
- 三维数字图像相关技术 /
- 量纲分析 /
- 响应面模型
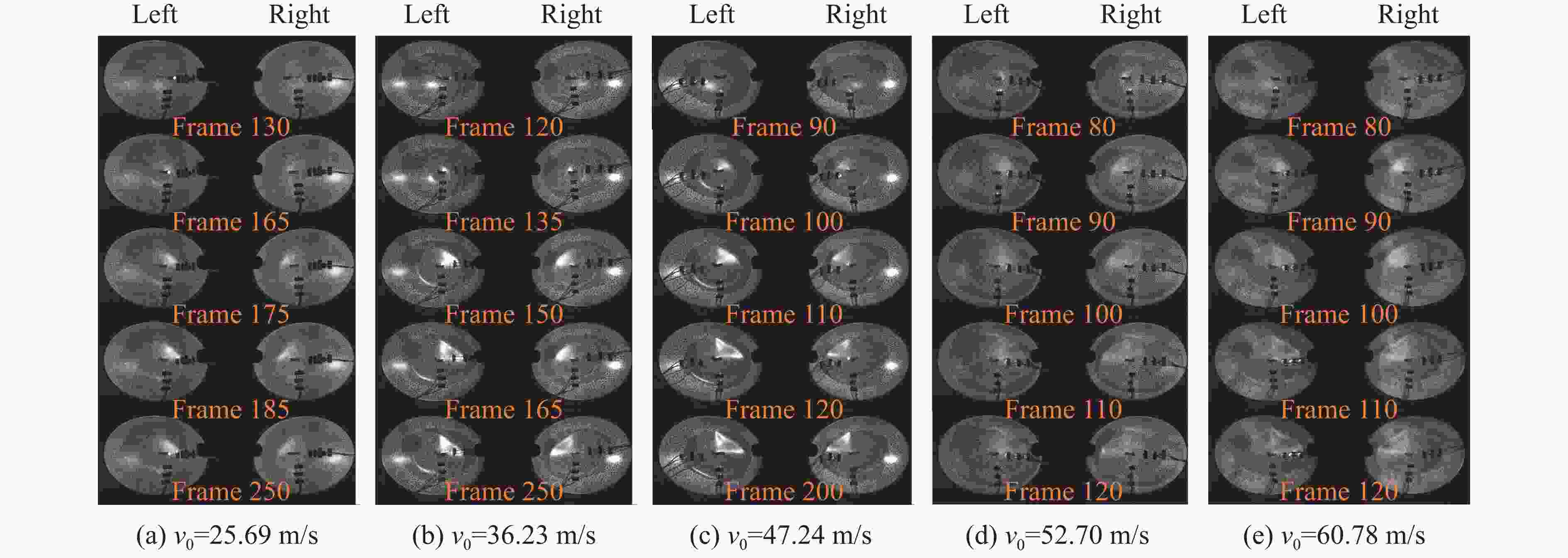
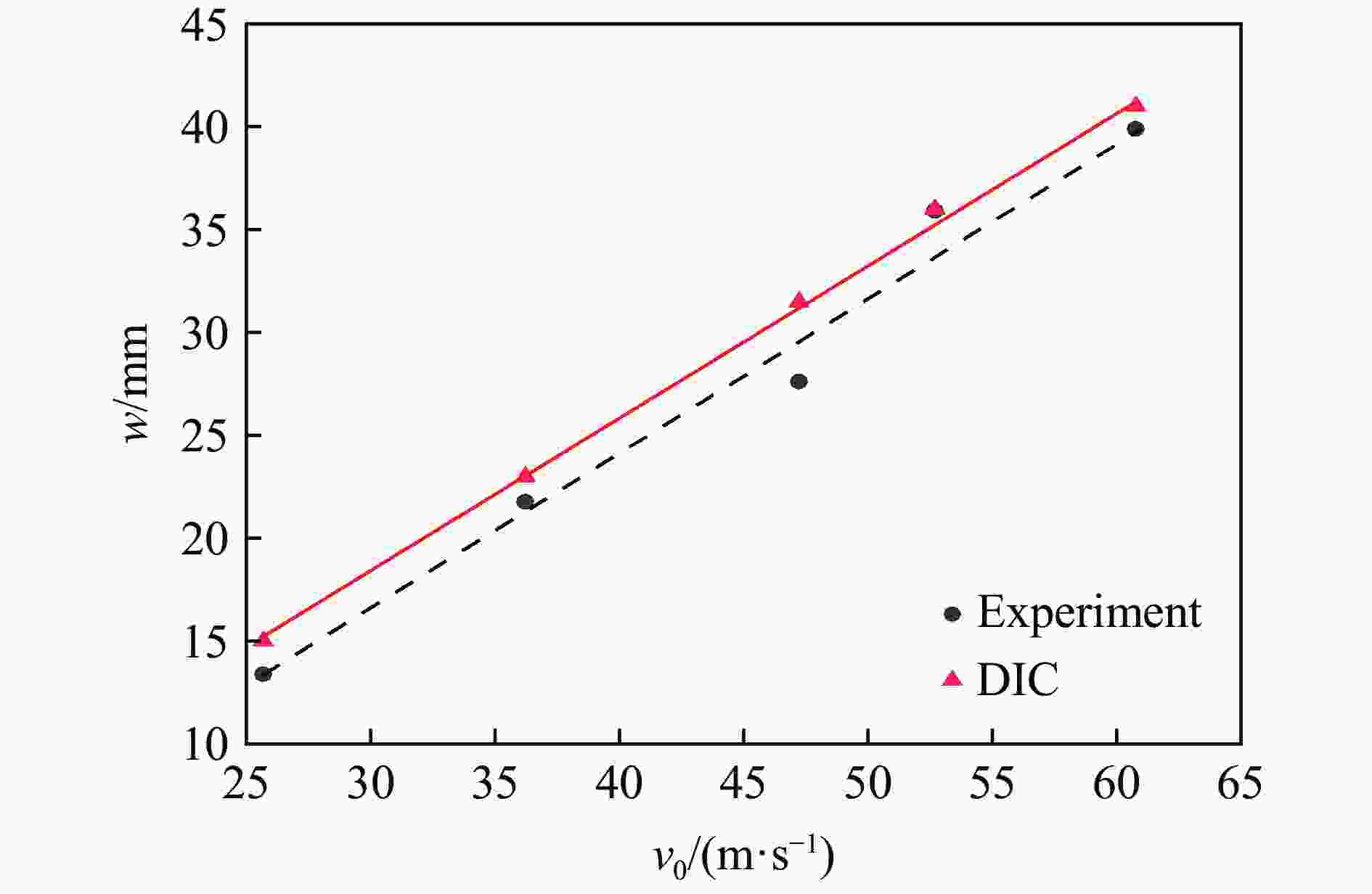
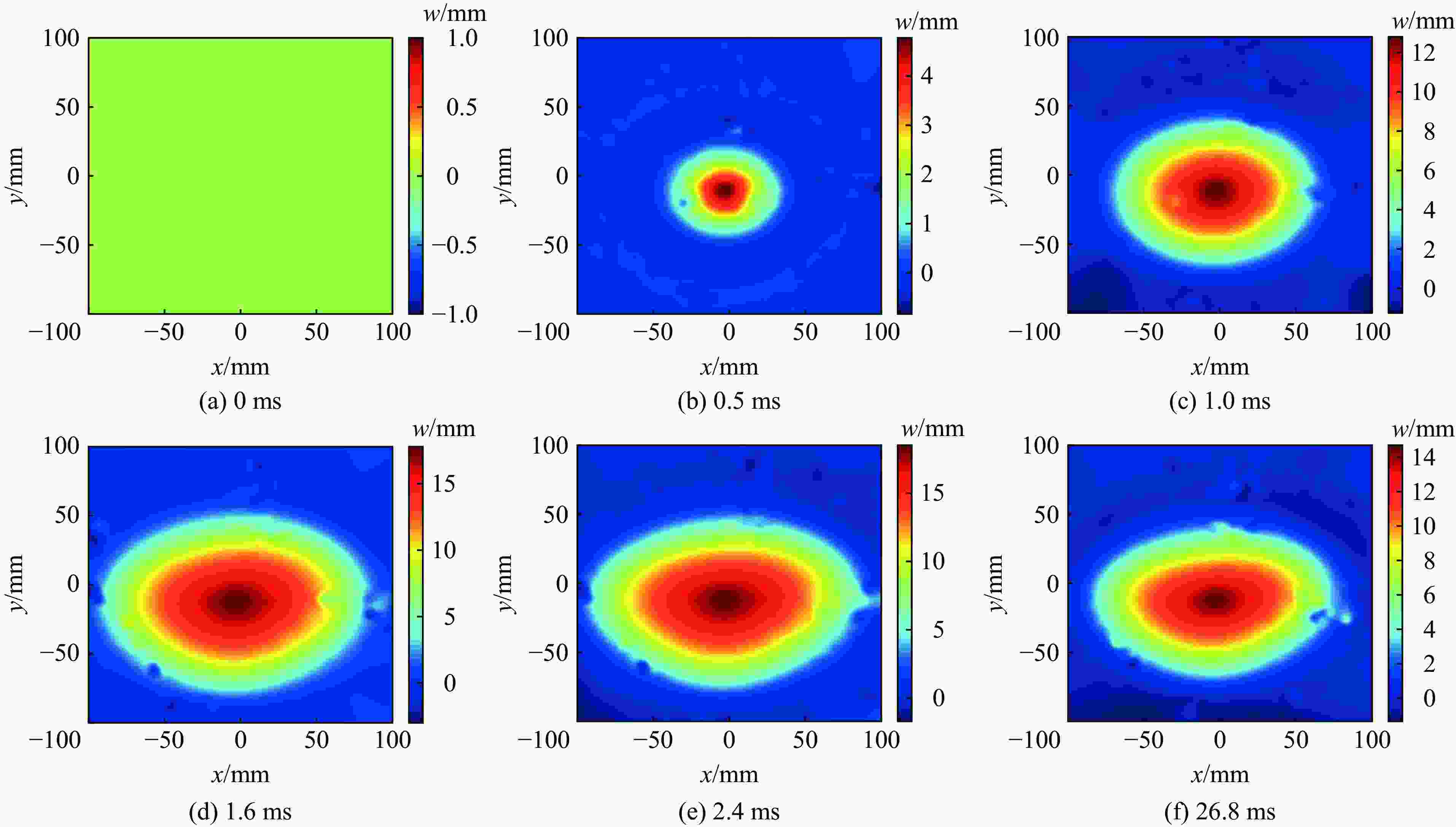
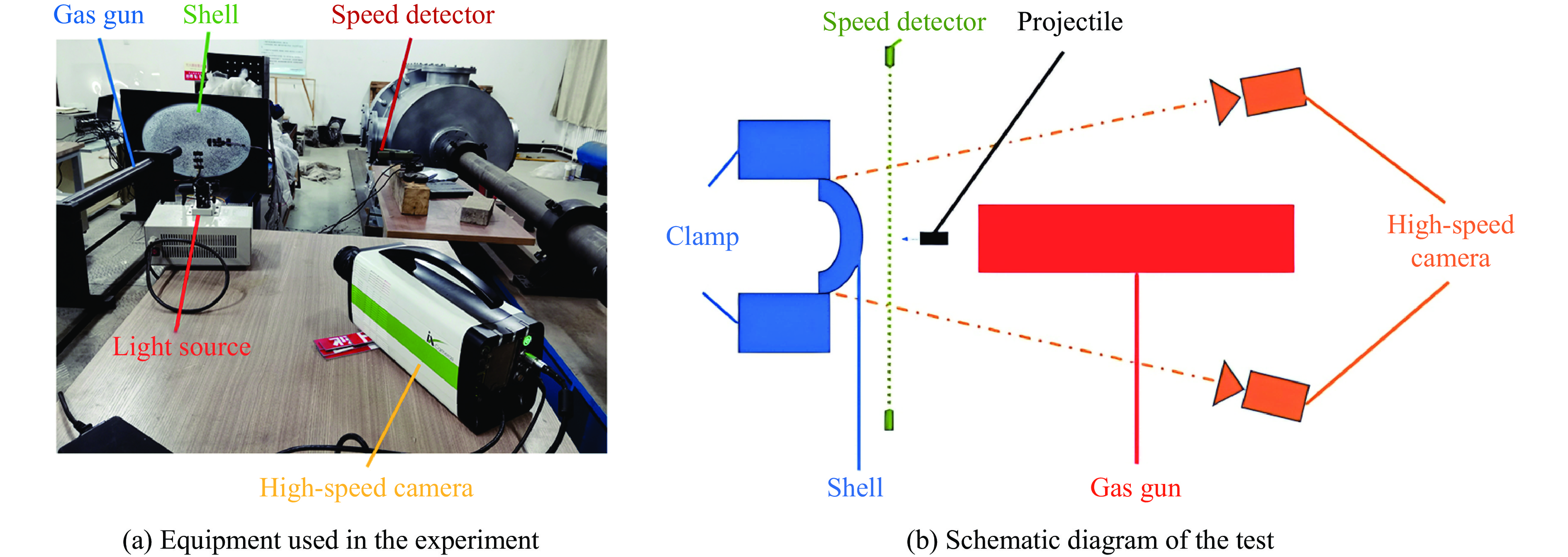
Abstract: In order to study the deformation characteristics of thin-walled ellipsoidal shells under localized impact loading, experimental investigations and numerical simulations were conducted. The global deformation characteristics, central dent depth and dent boundary of the recovery ellipsoidal shell impacted by cylindrical projectiles at different velocities were obtained by projectile impact tests on a light gas gun apparatus and three-dimensional digital image correlation (DIC) technology for deformation process record. The simulation analysis focused on the effects of three different curvature radii on the depression depth and the lengths of the major and minor axes of the ellipsoidal shell. The primary dimensionless independent variables on which the dimensionless deformation characteristics depend were determined by means of dimensional analysis. The influence of less significant parameters was reduced through parameter sensitivity analysis. Under the condition of maintaining consistent scaling ratios for material properties, projectile dimensions, and shell thickness, specific response surface function expressions between dimensionless deformation characteristics vs three curvature radii and velocity parameters were derived. A formula for predicting global deformation based on the depth of the depression and the depression boundary was proposed. The established expression can well describe the size effect and has a high prediction accuracy, and can provide reference for the design of impact load protection of large-sized curved thin shells in engineering.
- thin-walled ellipsoidal shell /
- impact load /
- stereo digital image correlation technology /
- dimensional analysis /
- response surface model

HTML全文

图 1 圆柱弹丸冲击椭球壳实验布置

Figure 1. Experimental field of cylindrical projectile impacting ellipsoidal shell

下载: 全尺寸图片幻灯片

图 2 椭球壳装配及尺寸示意图

Figure 2. Ellipsoidal shell assembly and dimension diagram

下载: 全尺寸图片幻灯片

图 3 不同冲击速度下椭球壳的动态变形过程

Figure 3. Dynamic deformation process of ellipsoidal shells impacted by projectiles at different velocities

下载: 全尺寸图片幻灯片

图 4 实验测量与DIC测量的中心凹深

Figure 4. Dimple depth measured by experiment and DIC

下载: 全尺寸图片幻灯片

图 5 第一组椭球壳不同时刻离面位移云图(v₀=25.69 m/s)

Figure 5. The first group of ellipsoidal shell displacement cloud images at different times (v₀=25.69 m/s)

下载: 全尺寸图片幻灯片

图 6 椭球壳凹陷区域长半轴L₁与短半轴L₂随冲击速度的变化

Figure 6. Variation of major axis L1 and minor axis L2 with impact velocity in ellipsoidal shell depression area

下载: 全尺寸图片幻灯片

图 7 薄壁浅椭球壳受圆柱形弹体冲击数值模拟模型

Figure 7. Numerical simulation model of shallow thin ellipsoidal shell subjected to cylindrical projectile impact

下载: 全尺寸图片幻灯片

图 8 实验与数值模拟全局变形形貌对比

Figure 8. Comparison between experimentally obtained global deformation features and simulation obtained global deformation features

下载: 全尺寸图片幻灯片

图 9 实验、DIC和数值模拟得到的凹陷深度和凹陷长短半轴对比

Figure 9. Comparison of dimple depth and dimple major axis and minor axis obtained by experimental, DIC, and simulation

下载: 全尺寸图片幻灯片

图 10 不同冲击速度下中心凹陷深度随曲率半径的变化

Figure 10. Variation of dimple depth with radius of curvature at different impact velocities

下载: 全尺寸图片幻灯片

图 11 不同冲击速度下凹陷长短半轴随曲率半径R₁的变化

Figure 11. Variation of concave length and length semi-axis with R₁ at different impact velocities

下载: 全尺寸图片幻灯片

图 12 不同冲击速度下凹陷长短半轴随曲率半径R₃的变化

Figure 12. Variation of concave length and length semi-axis with R₃ at different impact velocities

下载: 全尺寸图片幻灯片

图 13 各参数对变形特征影响的极差分析

Figure 13. Range chart of the deformation characteristics of each parameter

下载: 全尺寸图片幻灯片

图 14 预测模型凹深在不同速度及曲率半径下的适用范围

Figure 14. Predictive model᾽s applicable range for concave depth under different velocities and curvature radii

下载: 全尺寸图片幻灯片

图 15 预测模型凹陷边界在不同速度及曲率半径下的适用范围

Figure 15. Applicable range of the predictive model᾿s concave boundary under different velocities and curvature radii

下载: 全尺寸图片幻灯片

图 16 响应面模型全局变形对比数值模拟全局变形

Figure 16. Response surface model global deformation compared with simulated global deformation

下载: 全尺寸图片幻灯片

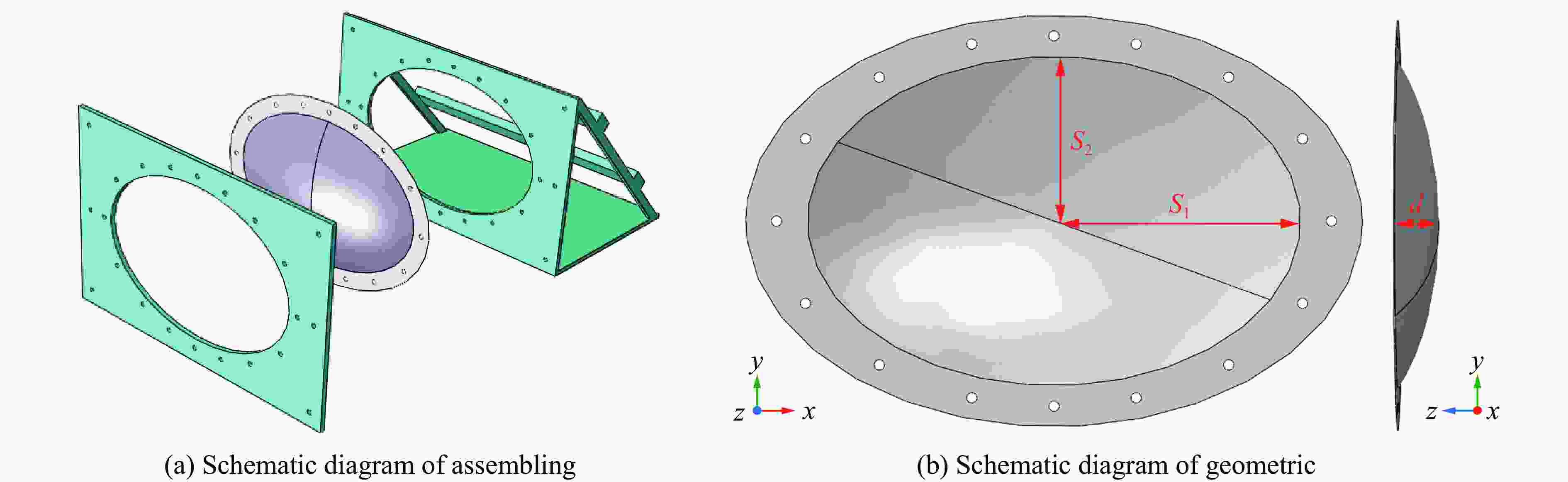
表 1 薄壁金属椭球壳几何与材料参数^[20]

Table 1. Geometric and material parameters of thin-walled metal ellipsoidal shells^[20]

S₁/mm	S₂/mm	d/mm	E/GPa	ρ/(kg∙m⁻³)	μ
240	160	40	70	2 700	0.3

下载: 导出CSV

表 2 5052Al的Johnson-Cook本构模型参数^[20]

Table 2. Johnson-Cook constitutive model parameters of 5052Al^[20]

A/MPa	B/MPa	C	n	m
121	327	0.009	0.544	1.12

下载: 导出CSV

表 3 物理量参数

Table 3. Physical quantity parameters

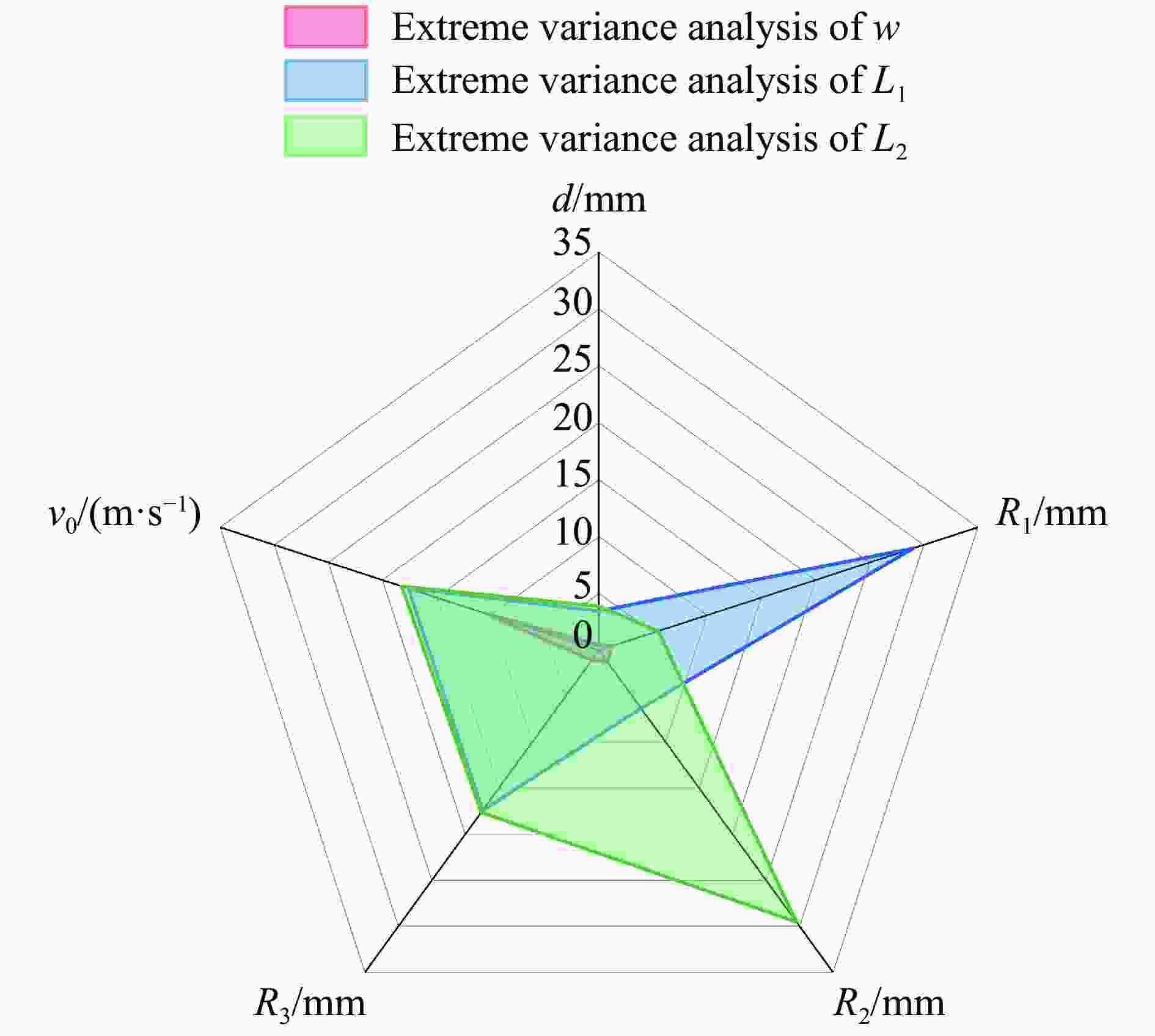
分析对象	参数	量纲	分析对象	参数	量纲
薄壁椭球壳	R₁	L	圆柱弹丸	L_s	L
	R₂	L		m_s	M
	R₃	L		R_s	L
	ρ	ML⁻³		E_s	ML⁻¹T⁻²
	E	ML⁻¹T⁻²		μ_s	1
	Y	ML⁻¹T⁻²		v₀	LT⁻¹
	μ	1
	h	L
	d	L

下载: 导出CSV

表 4 正交实验工况设计及数值模拟结果

Table 4. Orthogonal experimental design and simulation results

Case	d/mm	R₁/mm	R₂/mm	R₃/mm	v₀/(m·s⁻¹)	w/mm	L₁/mm	L₂/mm
1	50	200	200	200	30	15.14	47.1	47.1
2	50	240	240	240	35	19.31	64.8	64.8
3	50	280	280	280	40	22.72	70.7	70.7
4	50	320	320	320	45	26.87	82.7	82.7
5	60	200	240	280	45	24.85	54.0	62.3
6	60	240	200	320	40	21.12	53.1	46.3
7	60	280	320	200	35	20.29	79.5	89.6
8	60	320	280	240	30	16.28	71.9	63.9
9	70	200	280	320	35	17.92	42.6	55.0
10	70	240	320	280	30	15.56	50.3	63.2
11	70	280	200	240	45	25.39	76.0	58.0
12	70	320	240	200	40	23.30	94.2	73.6
13	80	200	320	240	40	22.09	55.1	80.4
14	80	240	280	200	45	26.84	78.7	90.0
15	80	280	240	320	30	15.19	51.5	45.8
16	80	320	200	280	35	18.28	66.2	46.5

下载: 导出CSV

表 5 响应面模型的计算工况

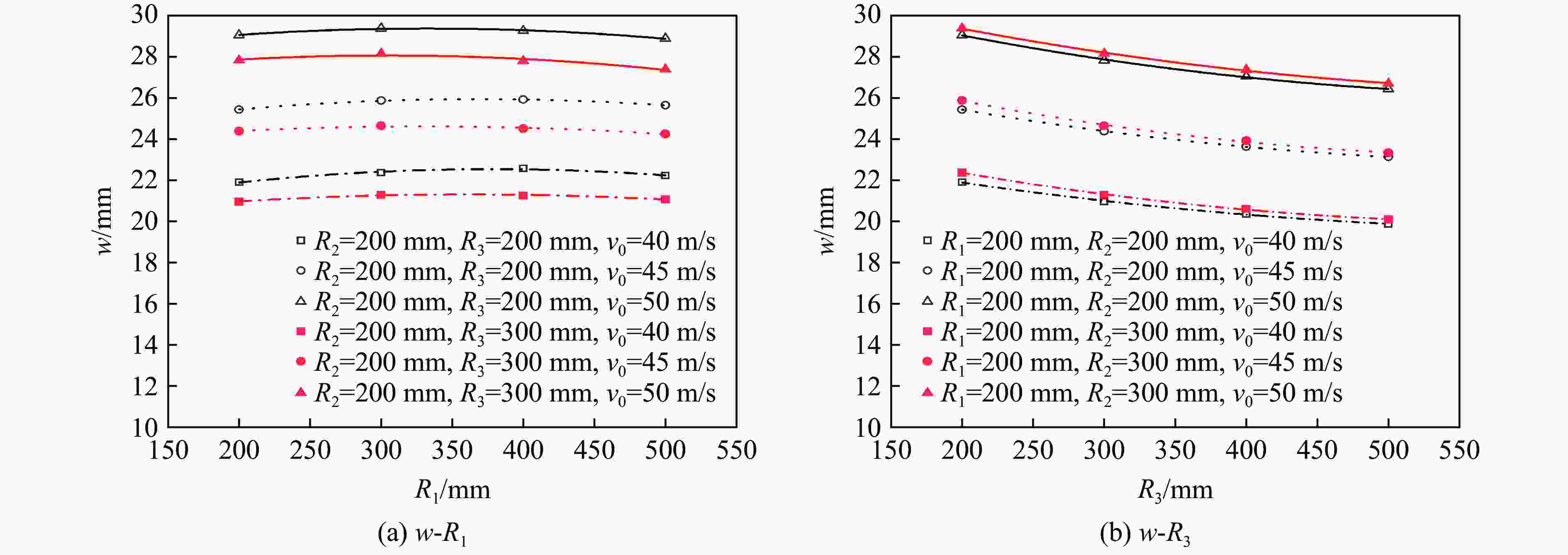
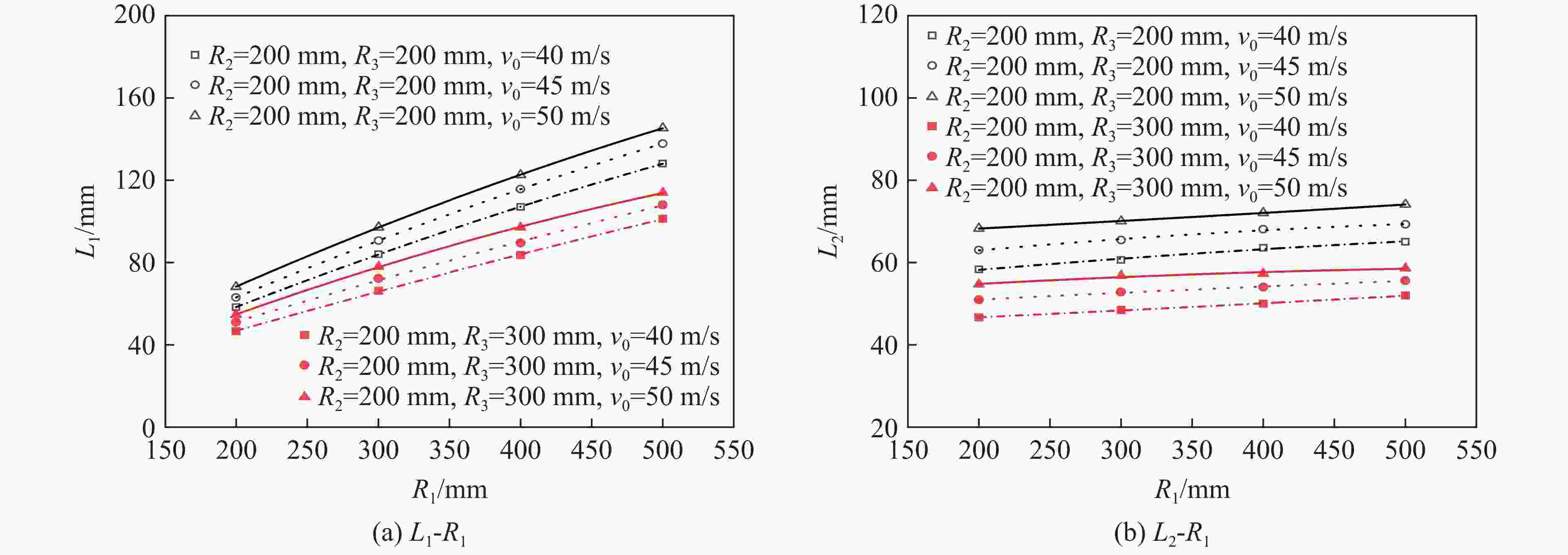
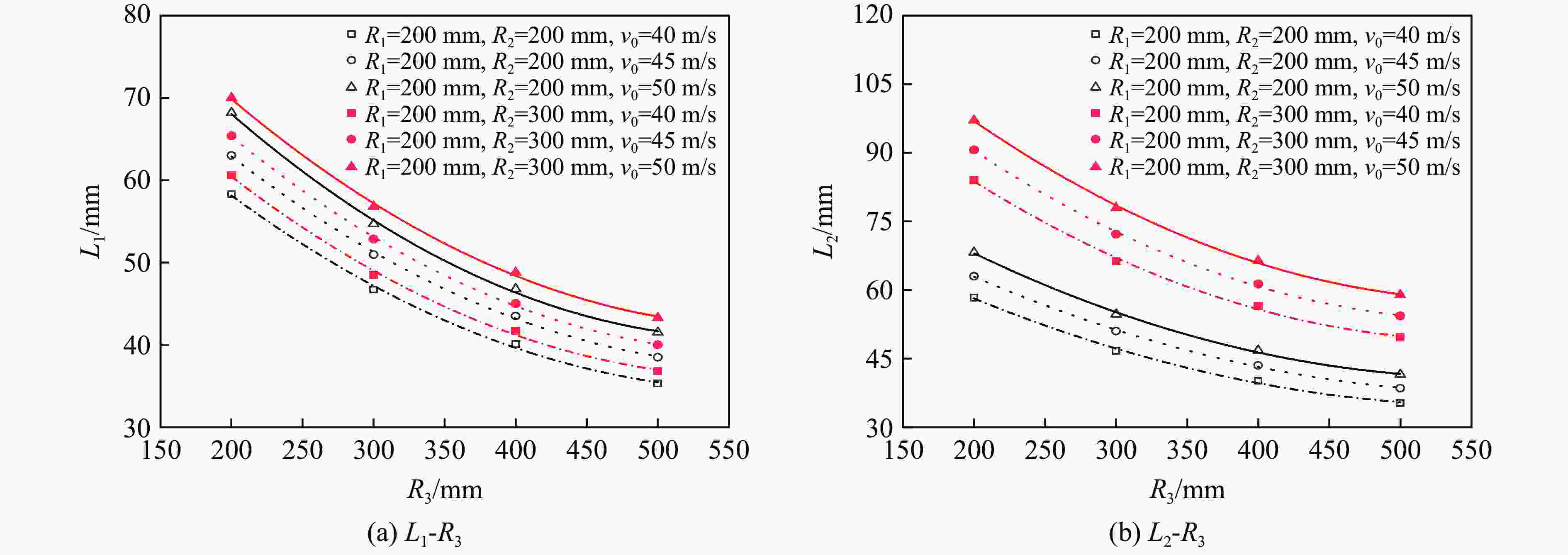
Table 5. Calculation condition of response surface model

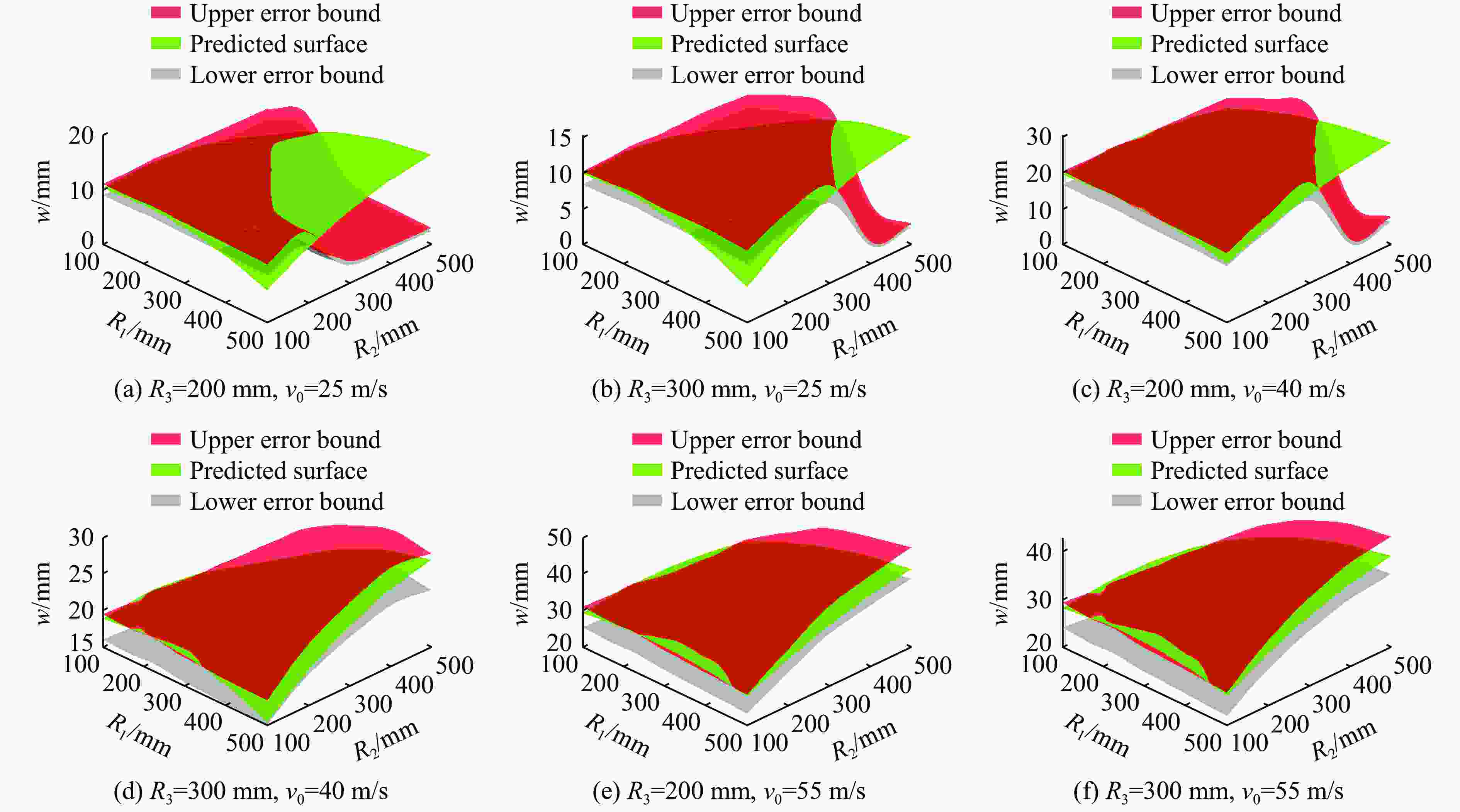
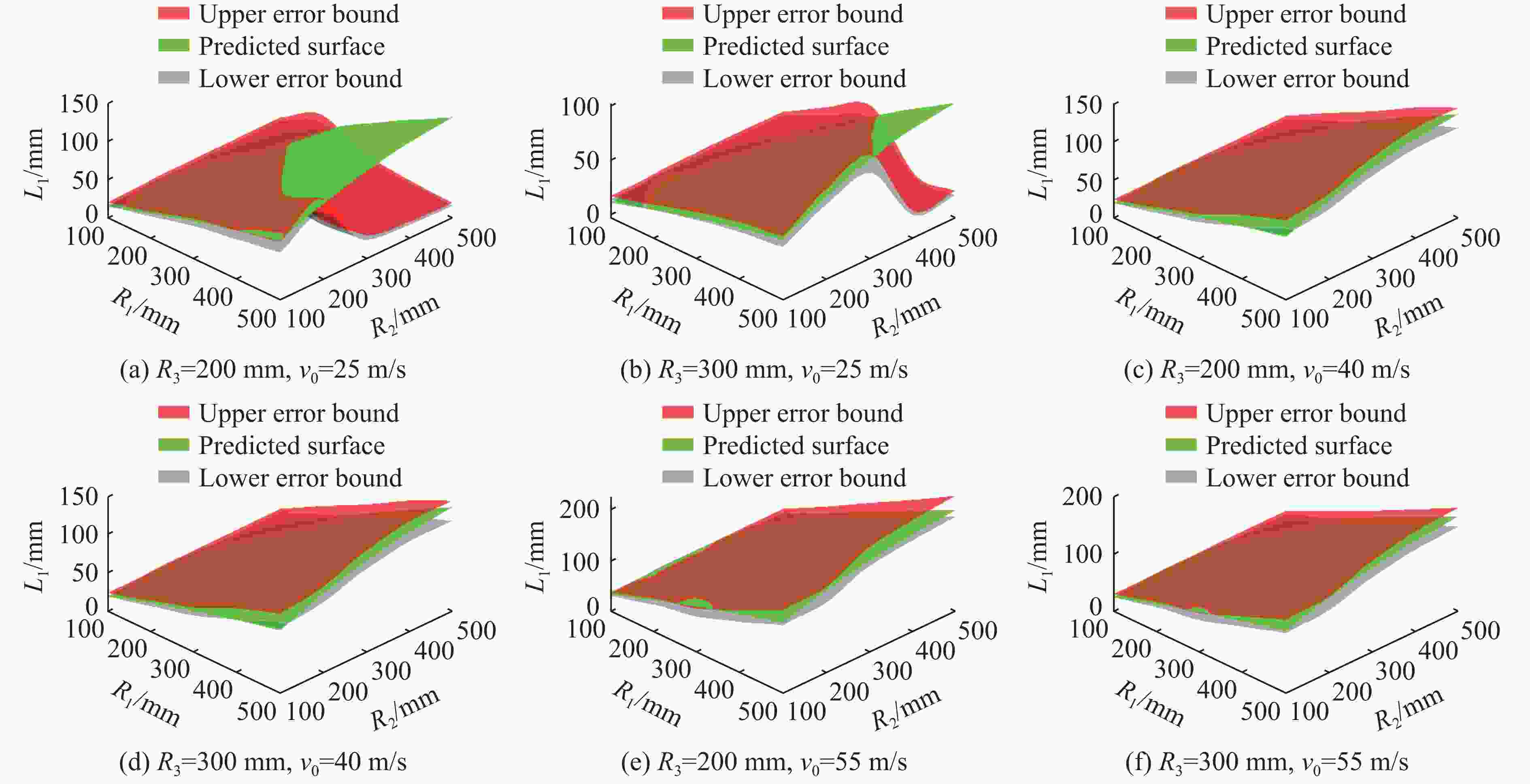
R₁/mm	R₂/mm	R₃/mm	v₀/(m·s⁻¹)	w/mm	L₁/mm	L₂/mm
200	200	200	35	18.45	52.9	52.9
200	300	200	35	18.95	55.5	77.0
200	400	200	35	19.15	57.4	99.4
300	300	200	35	20.37	85.0	85.0
300	400	200	35	20.64	87.0	113.0
200	200	200	40	21.90	58.3	58.3
200	300	200	40	22.37	60.6	84.0
200	400	200	40	22.57	63.5	107.0
300	300	200	40	24.09	92.7	92.7
300	400	200	40	24.82	95.7	123.5
200	200	200	45	25.43	63.0	63.0
200	300	200	45	25.87	65.4	90.6
200	400	200	45	25.91	68.0	115.6
300	300	200	45	27.90	99.6	99.6
300	400	200	45	28.82	102.5	132.9
200	200	200	50	29.05	68.2	68.2
200	300	200	50	29.38	70.0	97.1
200	400	200	50	29.26	72.0	122.5
300	300	200	50	31.63	106.0	106.0
300	400	200	50	32.98	109.6	141.8
200	200	300	35	17.67	42.5	42.5
200	300	300	35	18.00	44.4	60.0
200	400	300	35	18.08	45.6	76.4
300	300	300	35	19.43	66.9	66.9
300	400	300	35	19.89	67.5	86.4
400	400	300	35	20.98	94.4	94.4
200	200	300	40	20.96	46.7	46.7
200	300	300	40	21.29	48.5	66.3
200	400	300	40	21.26	50.0	83.6
300	300	300	40	23.10	73.6	73.6
300	400	300	40	23.53	76.0	97.7
400	400	300	40	24.77	102.8	102.8
200	200	300	45	24.38	51.0	51.0
200	300	300	45	24.64	52.83	72.2
200	400	300	45	24.51	54.0	89.4
300	300	300	45	26.70	79.5	79.5
300	400	300	45	27.19	81.8	104.6
400	400	300	45	28.56	110.8	110.8
200	200	300	50	27.83	54.7	54.7
200	300	300	50	28.15	56.8	78.0
200	400	300	50	27.80	57.3	97.1
300	300	300	50	30.42	85.3	85.3
300	400	300	50	30.86	87.6	111.2
400	400	300	50	32.63	118.6	118.6
200	200	400	35	17.11	36.3	36.3
200	300	400	35	17.36	37.5	50.7
200	400	400	35	17.14	38.5	62.8
200	200	400	40	20.37	40.1	40.1
200	300	400	40	20.60	41.7	56.5
200	400	400	40	20.31	42.3	70.0
200	200	400	45	23.63	43.5	43.5
200	300	400	45	23.92	45.0	61.3
200	400	400	45	23.51	45.7	76.2
200	200	400	50	27.04	46.8	46.8
200	300	400	50	27.37	48.8	66.4
200	400	400	50	26.81	48.8	81.9
300	300	400	35	18.70	56.7	56.7
300	400	400	35	19.14	58.8	74.6
300	300	400	40	22.22	62.5	62.5
300	400	400	40	22.72	64.8	81.9
300	300	400	45	25.87	68.2	68.2
300	400	400	45	26.30	70.2	88.8
300	300	400	50	29.52	73.7	73.7
300	400	400	50	29.84	75.3	94.6

下载: 导出CSV

表 6 响应面模型误差

Table 6. Response surface model error

变形特征	R²	δ_RAAE	δ_RMAE	δ_RMS
w/h	0.995	0.015	0.032	0.019
L₁/h	0.996	0.012	0.036	0.017
L₂/h	0.996	0.018	0.05	0.025

下载: 导出CSV

表 7 数值模拟变形特征响应面预测变形特征的对比

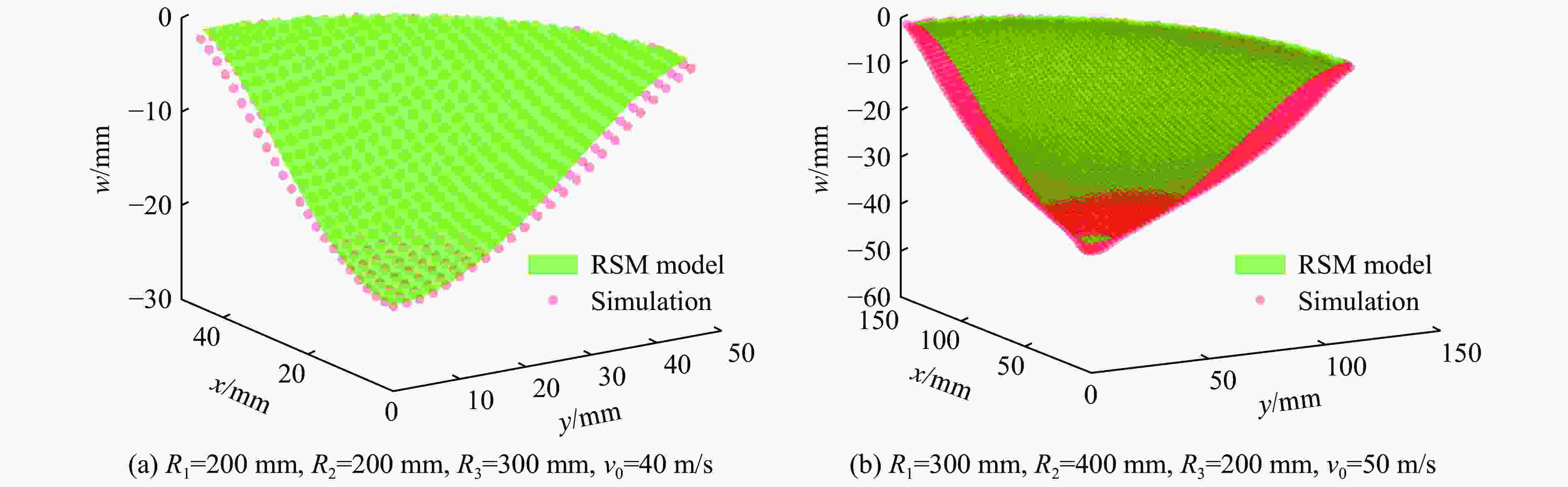
Table 7. Simulated deformation characteristics compared with response surface predicted deformation features

Material	h/mm	R₁/mm	R₂/mm	R₃/mm	v₀/(m·s⁻¹)	w/mm	w_a/mm	L₁/mm	L_1a/mm	L₂/mm	L_2a/mm
Al	0.5	200	160	180	15	12.5	12.5	46.5	45.5	37.7	38.1
Al	2.0	450	500	480	80	27.1	29.2	90.8	96.8	97.2	104.9
Steel	0.5	150	100	200	30	7.5	10.8	24.0	28.7	17.8	21.9

下载: 导出CSV

参考文献(21)

[1]	LIM H K, LEE J S. On the structural behavior of ship’s shell structures due to impact loading [J]. International Journal of Naval Architecture and Ocean Engineering, 2018, 10(1): 103–118. DOI: 10.1016/j.ijnaoe.2017.03.002.
[2]	MOHAMMAD Z, GUPTA P K, BAQI A, et al. Ballistic performance of monolithic and double layered thin-metallic hemispherical shells at normal and oblique impact [J]. Thin-Walled Structures, 2021, 159: 107257. DOI: 10.1016/j.tws.2020.107257.
[3]	UPDIKE D P, KALNINS A. Axisymmetric behavior of an elastic spherical shell compressed between rigid plates [J]. Journal of Applied Mechanics, 1970, 37(3): 635–640. DOI: 10.1115/1.3408592.
[4]	UPDIKE D P. On the large deformation of a rigid-plastic spherical shell compressed by a rigid plate [J]. Journal of Engineering for Industry, 1972, 94(3): 949–955. DOI: 10.1115/1.3428276.
[5]	KITCHING R, HOULSTON R, JOHNSON W. A theoretical and experimental study of hemispherical shells subjected to axial loads between flat plates [J]. International Journal of Mechanical Sciences, 1975, 17(11/12): 693–703. DOI: 10.1016/0020-7403(75)90072-7.
[6]	GUPTA N K, MOHAMED SHERIFF N, VELMURUGAN R. Experimental and numerical investigations into collapse behaviour of thin spherical shells under drop hammer impact [J]. International Journal of Solids and Structures, 2007, 44(10): 3136–3155. DOI: 10.1016/j.ijsolstr.2006.09.014.
[7]	WEN H M. Large plastic deformation of spherical shells under impact by blunt-ended missiles [J]. International Journal of Pressure Vessels and Piping, 1997, 73(2): 147–152. DOI: 10.1016/S0308-0161(97)00043-4.
[8]	宁建国, 杨桂通. 球形扁壳在冲击载荷作用下的超临界变形 [J]. 爆炸与冲击, 1992, 12(3): 206–212. DOI: 10.11883/1001-1455(1992)03-0206-7. NING J G, YANG G T. Supercritical deformations of shallow spherical shells under impact [J]. Explosion and Shock Waves, 1992, 12(3): 206–212. DOI: 10.11883/1001-1455(1992)03-0206-7.
[9]	LI J Q, REN H L, NING J G. Deformation and failure of thin spherical shells under dynamic impact loading: experiment and analytical model [J]. Thin-Walled Structures, 2021, 161: 107403. DOI: 10.1016/j.tws.2020.107403.
[10]	ZHENG J, LI K, LIU S, et al. Effect of shape imperfection on the buckling of large-scale thin-walled ellipsoidal head in steel nuclear containment [J]. Thin-Walled Structures, 2018, 124: 514–522. DOI: 10.1016/j.tws.2018.01.001.
[11]	PALIWAL D N, GUPTA R, JAIN A. Stress analysis of ellipsoidal shell on an elastic foundation [J]. International Journal of Pressure Vessels and Piping, 1993, 56(2): 229–242. DOI: 10.1016/0308-0161(93)90095-B.
[12]	PATEL P R, GILL S S. Experiments on the buckling under internal pressure of thin torispherical ends of cylindrical pressure vessels [J]. International Journal of Mechanical Sciences, 1978, 20(3): 159–175. DOI: 10.1016/0020-7403(78)90003-6.
[13]	BUSHNELL D. Nonsymmetric buckling of internally pressurized ellipsoidal and torispherical elastic-plastic pressure vessel heads [J]. Journal of Pressure Vessel Technology, 1977, 99(1): 54–63. DOI: 10.1115/1.3454520.
[14]	CHAO Y J, SUTTON M A. Stress analysis of ellipsoidal shell with radial nozzle [J]. International Journal of Pressure Vessels and Piping, 1985, 21(2): 89–108. DOI: 10.1016/0308-0161(85)90042-0.
[15]	ROSS C T F, HUAT B H, CHEI T B, et al. The buckling of GRP hemi-ellipsoidal dome shells under external hydrostatic pressure [J]. Ocean Engineering, 2003, 30(5): 691–705. DOI: 10.1016/s0029-8018(02)00039-2.
[16]	BLACHUT J, JAISWAL O R. On the choice of initial geometric imperfections in externally pressurized shells [J]. Journal of Pressure Vessel Technology, 1999, 121(1): 71–76. DOI: 10.1115/1.2883670.
[17]	SMITH P, BŁACHUT J. Buckling of externally pressurized prolate ellipsoidal domes [J]. Journal of Pressure Vessel Technology, 2008, 130(1): 011210. DOI: 10.1115/1.2834457.
[18]	LIU L, LI J Q. Dynamic deformation and perforation of ellipsoidal thin shell impacted by flat-nose projectile [J]. Materials, 2022, 15(12): 4124. DOI: 10.3390/ma15124124.
[19]	陈旭东, 叶康生. 中厚椭球壳自由振动动力刚度法分析 [J]. 振动与冲击, 2016, 35(6): 85–90. DOI: 10.13465/j.cnki.jvs.2016.06.015. CHEN X D, YE K S. Free vibration analysis of moderately thick elliptical shells using the dynamic stiffness method [J]. Journal of Vibration and Shock, 2016, 35(6): 85–90. DOI: 10.13465/j.cnki.jvs.2016.06.015.
[20]	MA T B, SHEN Y, NING J G, et al. Analysis on dynamic shear fracture based on a novel damage evolution model [J]. International Journal of Impact Engineering, 2024, 183: 104810. DOI: 10.1016/j.ijimpeng.2023.104810.
[21]	陈刚, 陈忠富, 徐伟芳, 等. 45钢的J-C损伤失效参量研究 [J]. 爆炸与冲击, 2007, 27(2): 131–135. DOI: 10.11883/1001-1455(2007)02-0131-05. CHEN G, CHEN Z F, XU W F, et al. Investigation on the J-C ductile fracture parameters of 45 steel [J]. Explosion and Shock Waves, 2007, 27(2): 131–135. DOI: 10.11883/1001-1455(2007)02-0131-05.