钨合金弹丸侵彻钢靶的数值模拟方法

位国旭; 崔浩; 周昊; 杨贵涛; 郭锐

doi:10.11883/bzycj-2024-0147

钨合金弹丸侵彻钢靶的数值模拟方法

doi: 10.11883/bzycj-2024-0147

南京理工大学机械工程学院，江苏南京210094

基金项目: 国家自然科学基金(12202200，11972197，21875109)；江苏省研究生科研与实践创新计划(KYCX23_0510)；中国博士后科学基金(2022M711641)

详细信息

作者简介:
位国旭（1997－　），男，博士研究生，wei_guoxu@163.com

通讯作者:
郭　锐（1980－　），男，博士，教授，guorui@njust.edu.cn

中图分类号: O383; TJ012.4
计量
- 文章访问数: 208
- HTML全文浏览量: 25
- PDF下载量: 84
- 被引次数: 0
出版历程
- 收稿日期: 2024-05-20
- 修回日期: 2024-12-12
- 网络出版日期: 2024-12-17

Numerical simulation method for tungsten alloy projectilepenetration into steel target

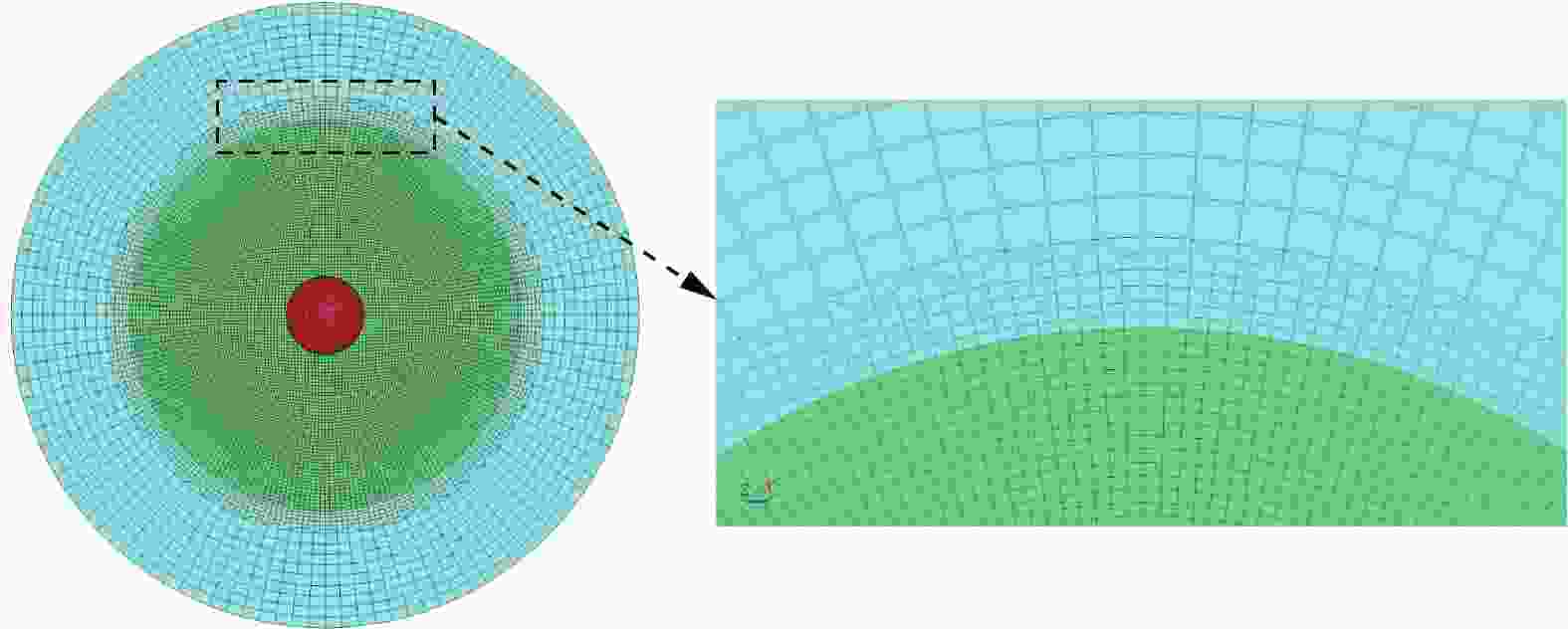
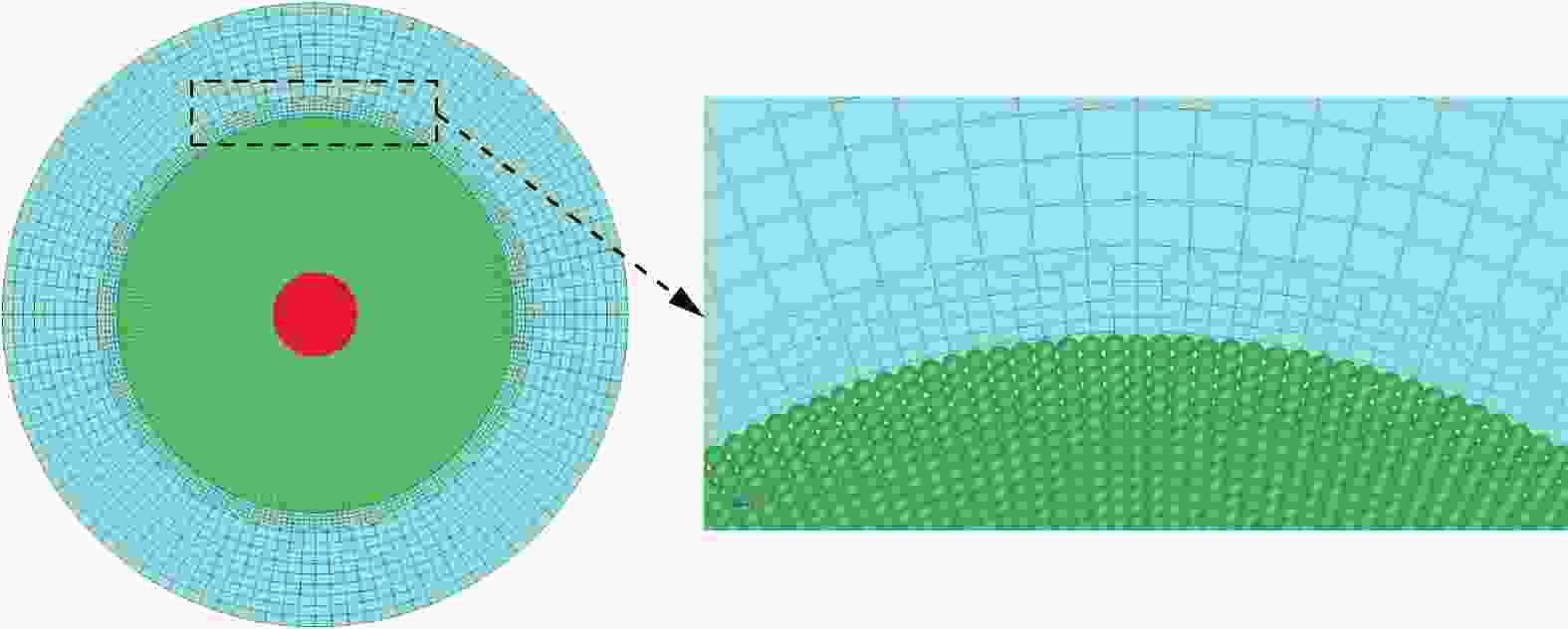
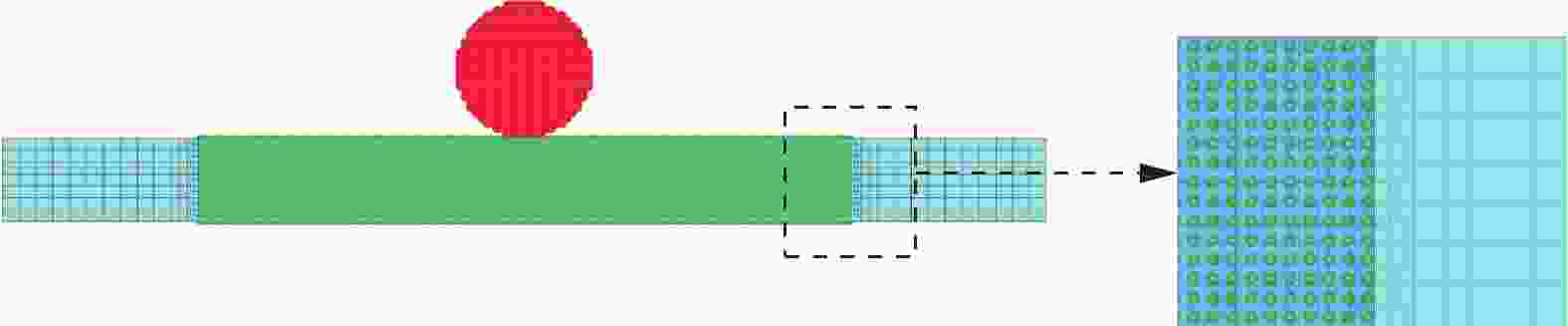
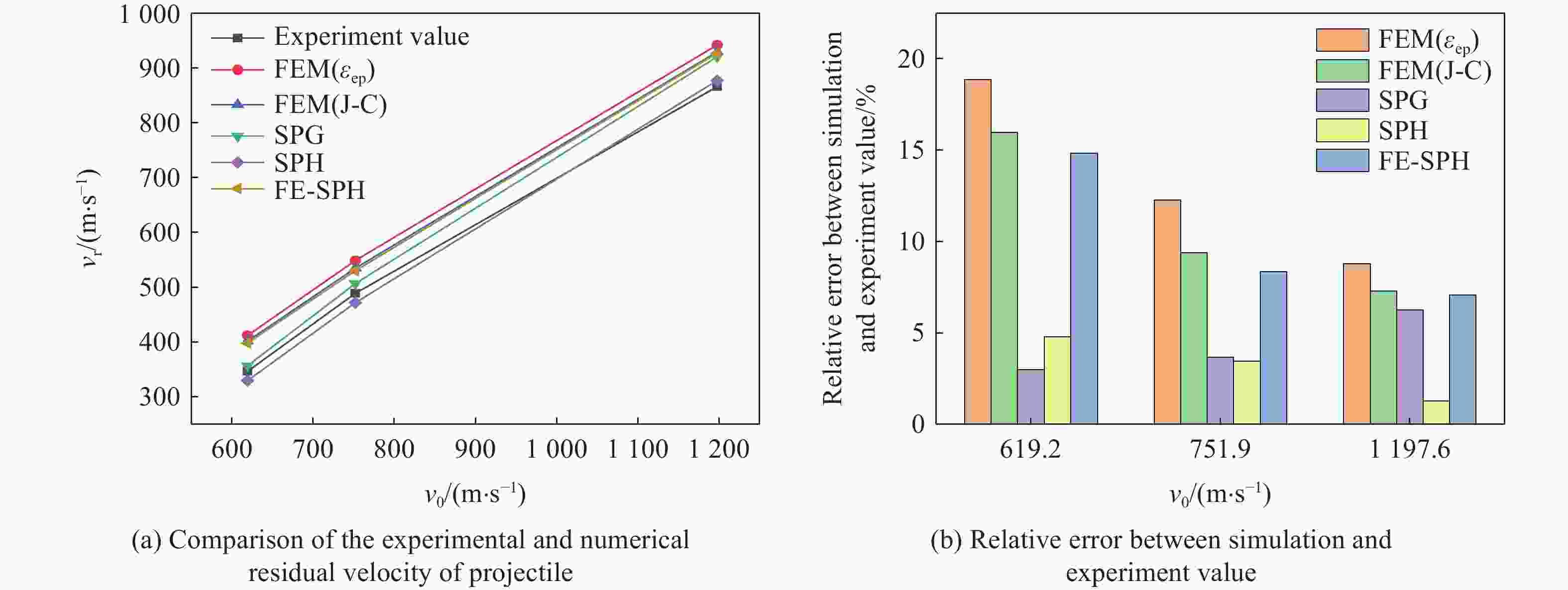
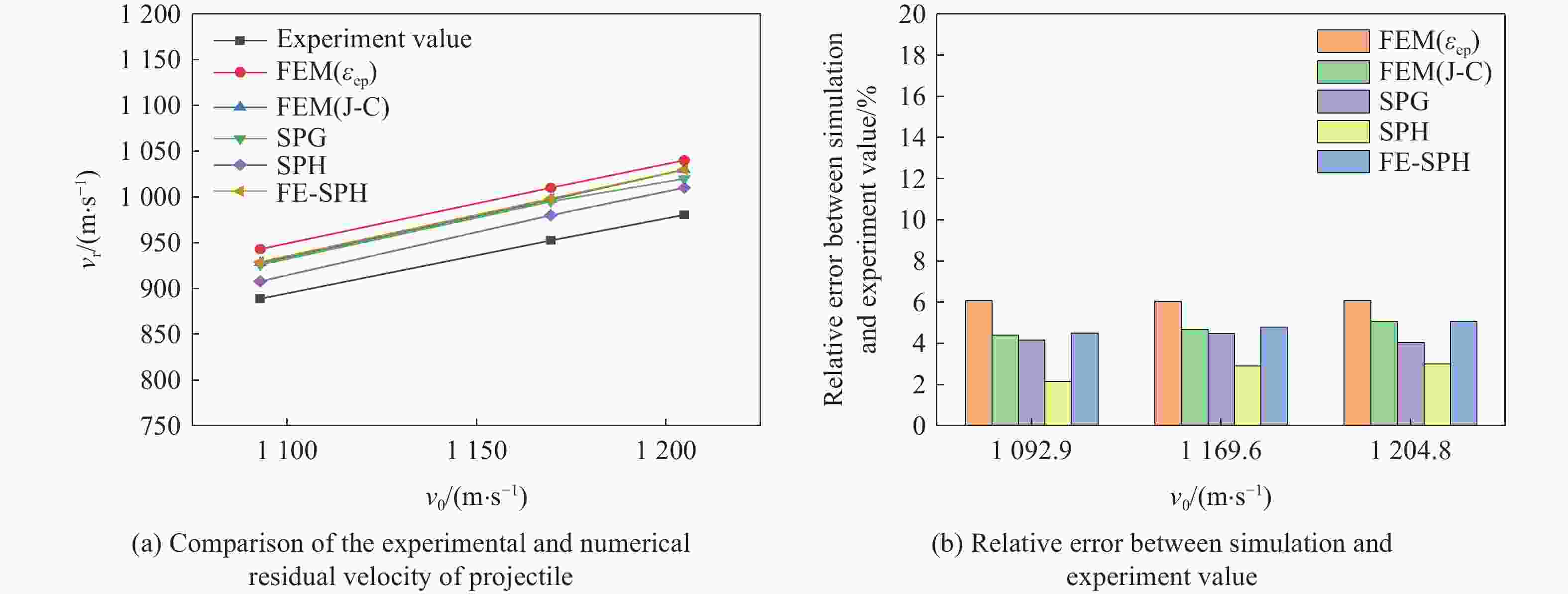
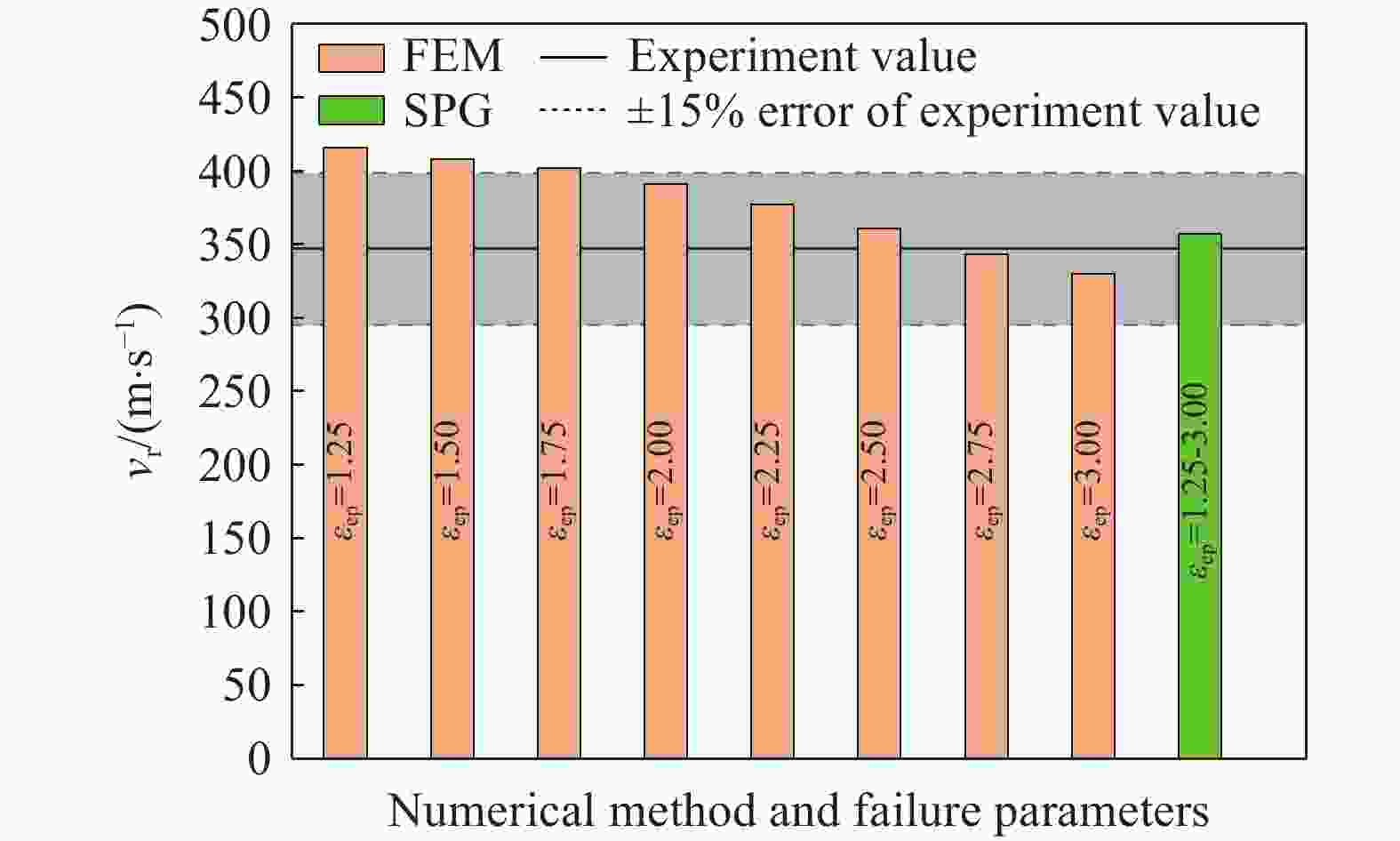
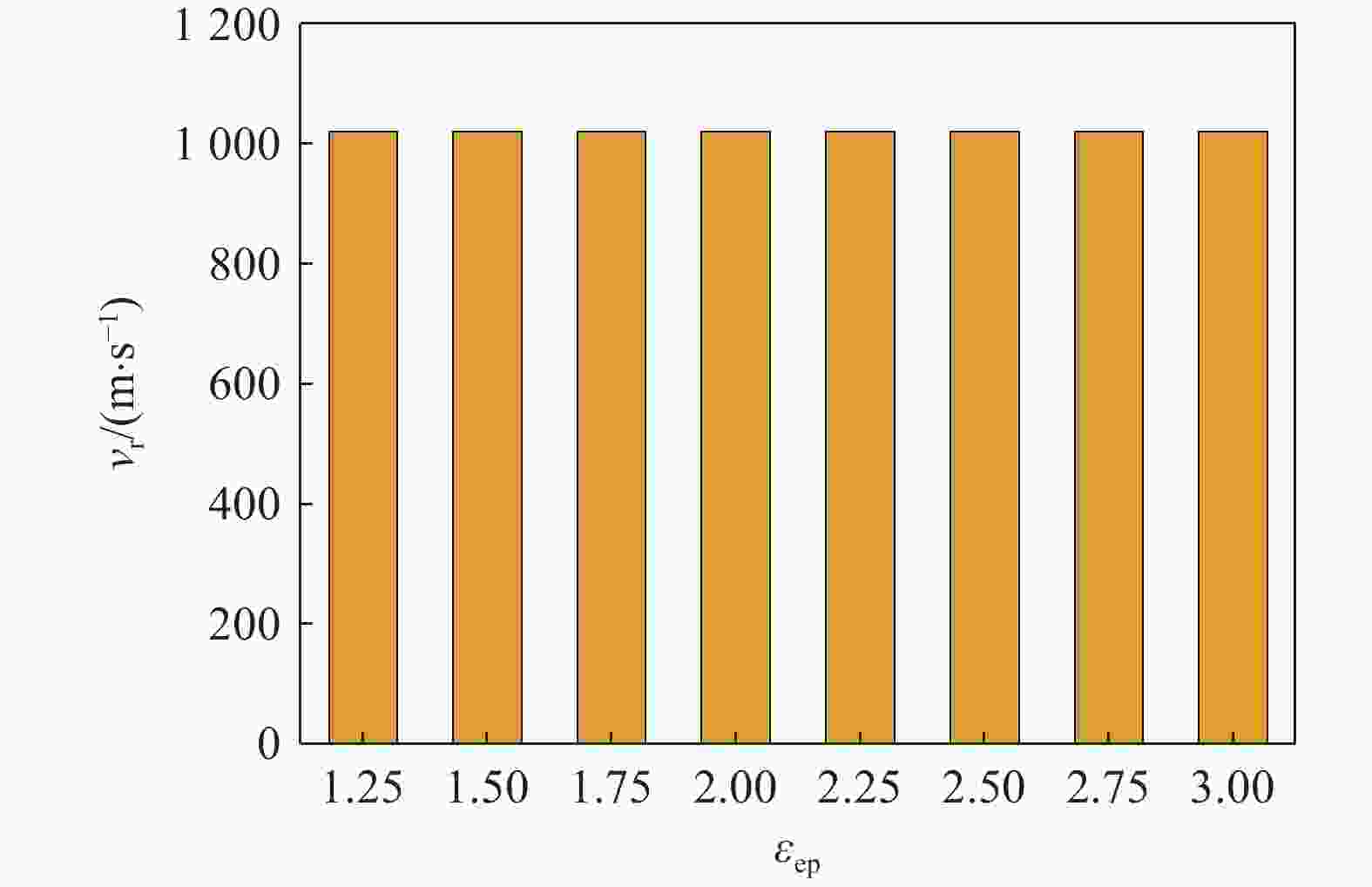
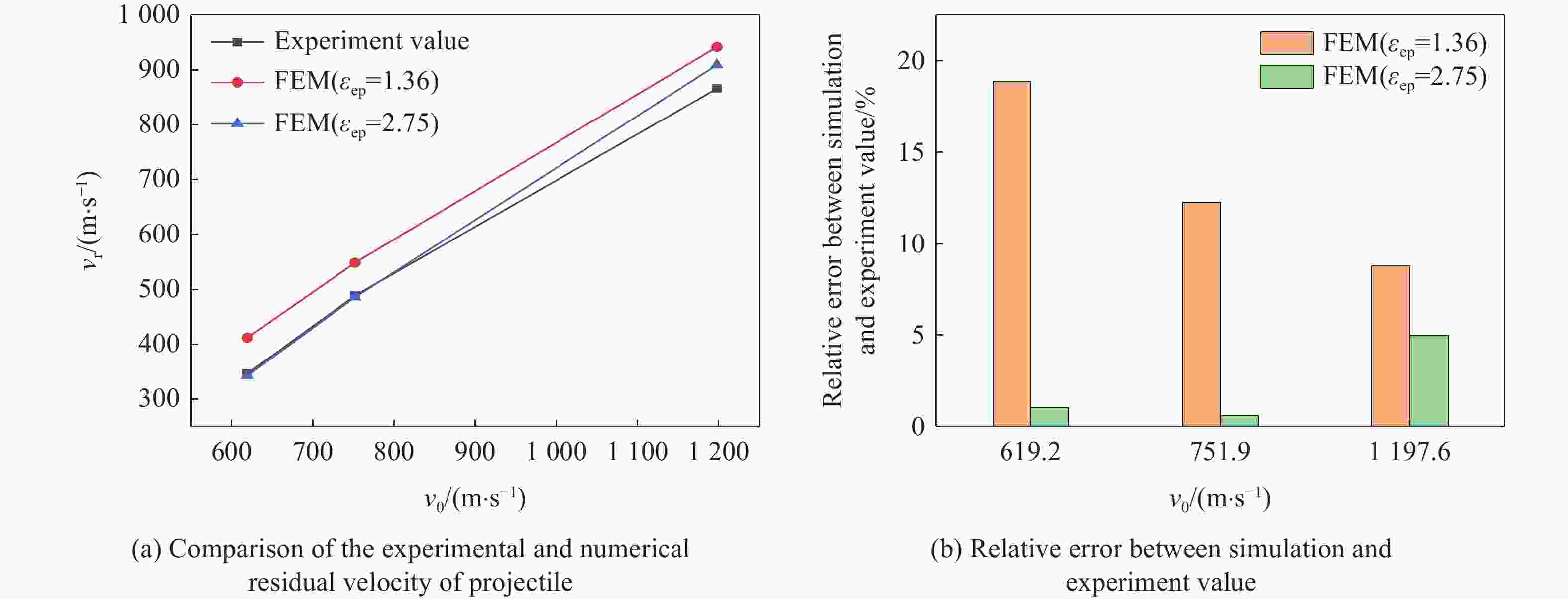
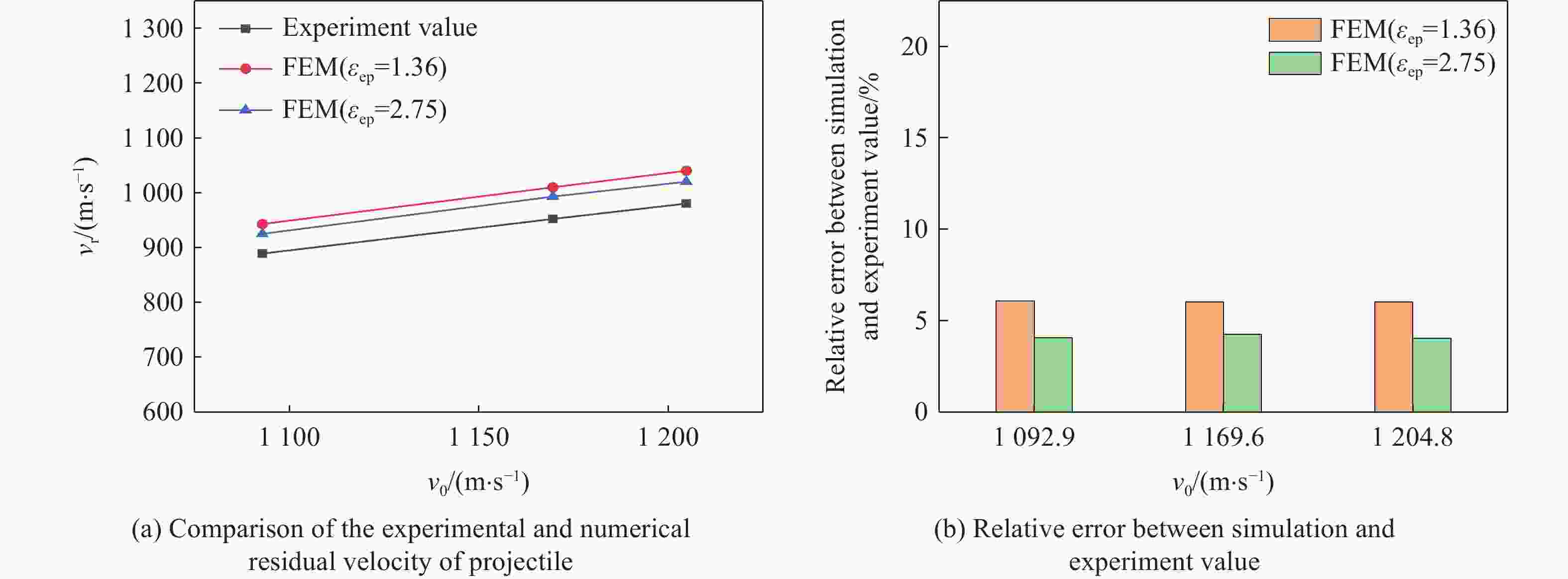
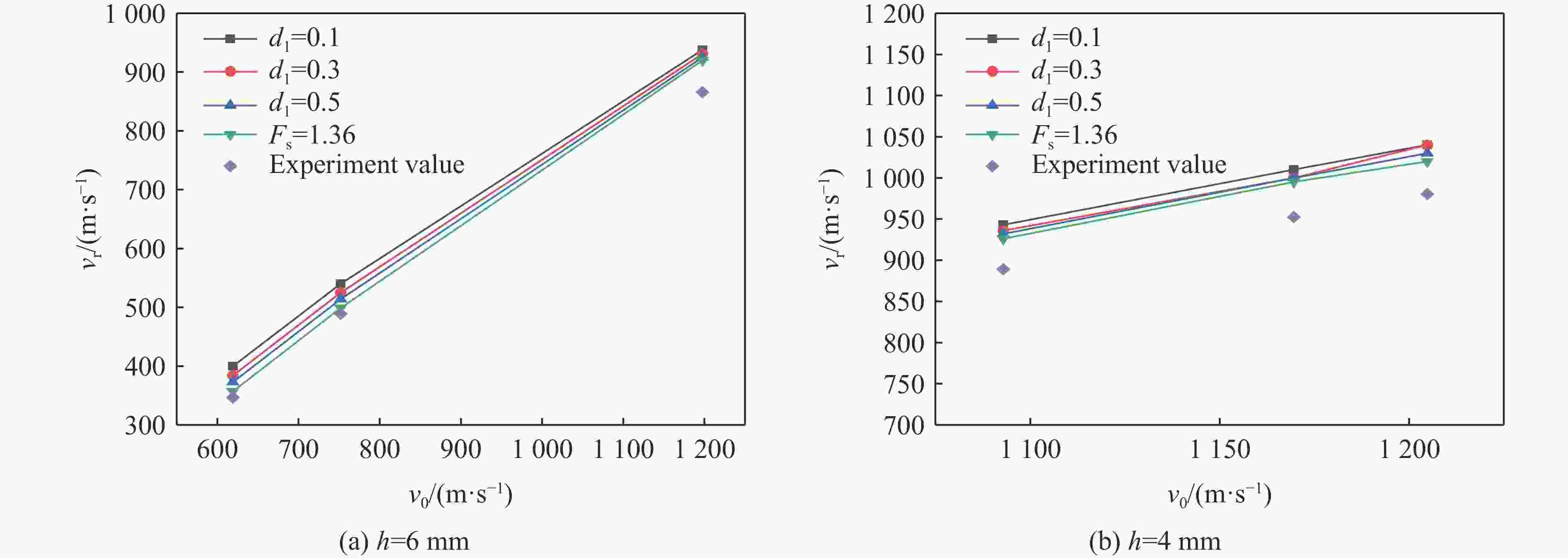
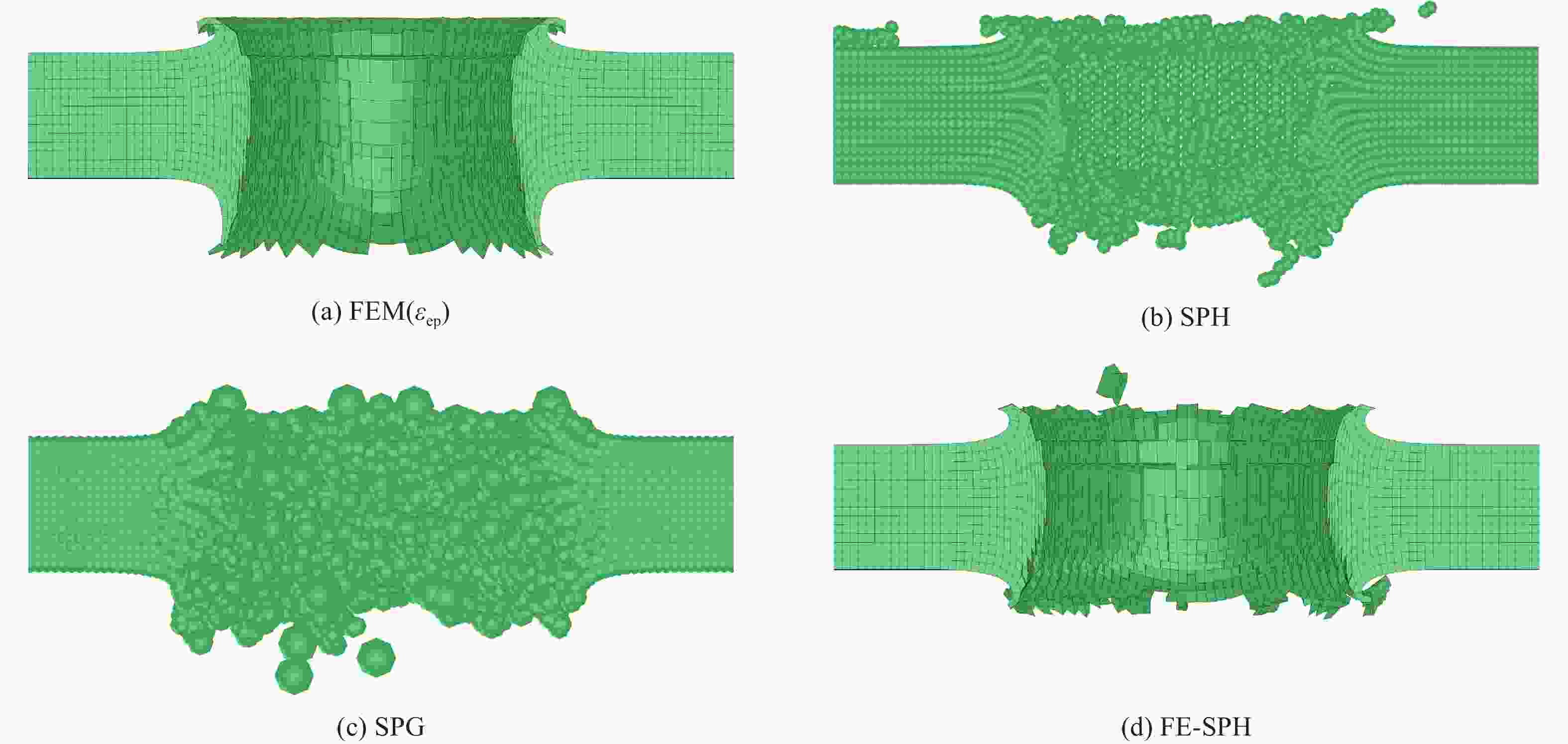
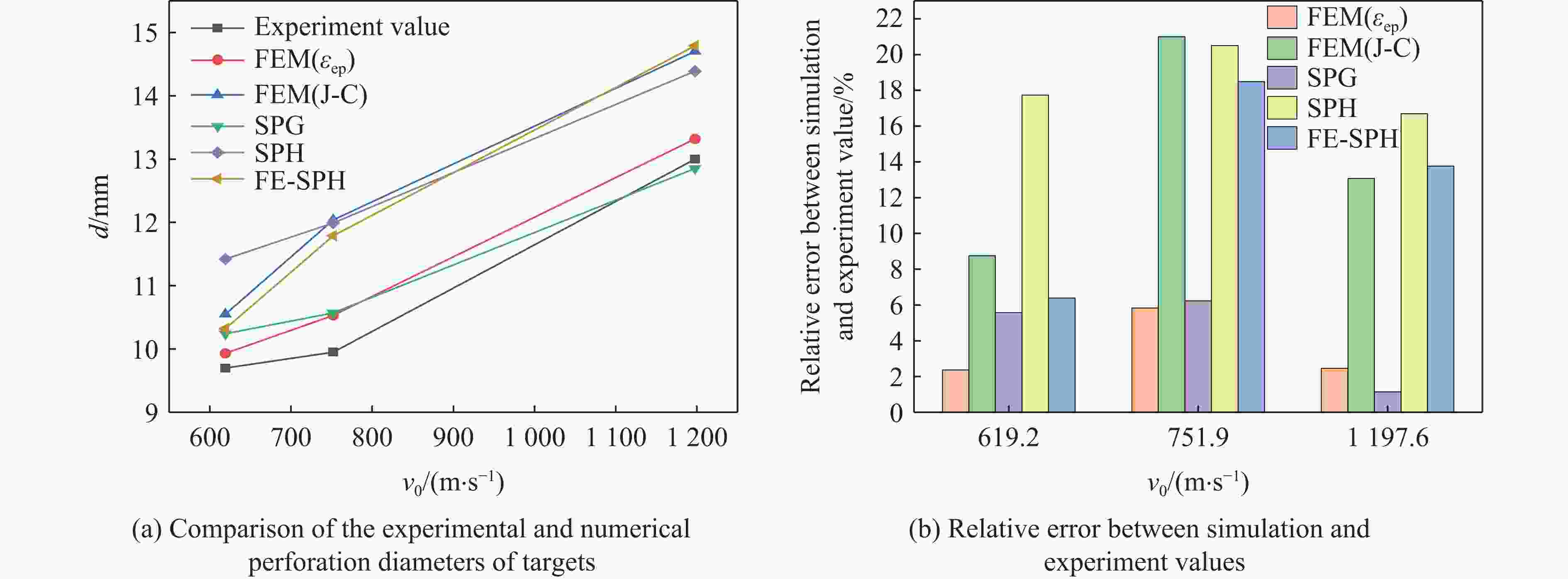
School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China

摘要

摘要: 为了更好地量化表征钨合金弹丸侵彻靶板过程，分别采用FEM（finite element method）、SPG（smoothed particle Galerkin）、SPH（smoothed particle hydrodynamics）、FE-SPH（finite element-smoothed particle hydrodynamics）自适应数值模拟方法，对钨合金弹丸侵彻Q235A钢靶开展了数值模拟计算，对比了4种数值模拟方法在描述弹丸侵彻穿靶后，弹丸剩余速度、靶板穿孔孔径以及弹丸穿靶后二次破片生成及其分布方面的优势和不足。结果表明：在描述弹丸剩余速度方面，由于FEM方法在处理材料失效问题时是基于单元侵蚀算法，因此FEM方法以及FE-SPH自适应方法严格依赖于失效准则以及失效参数的选择，而SPG方法在键失效模式下无需调整失效参数就可以得到相对准确的结果；在描述靶板穿孔孔径上，FEM以及FE-SPH自适应方法具有精确的物质边界，可以精确刻画穿孔形貌特征，但不同失效准则下的靶板穿孔直径相差较大；SPG方法对失效参数不敏感，可以准确预测靶板的穿孔直径；在弹丸穿靶后二次破片的生成及其分布方面，FE-SPH自适应以及SPH方法均能对二次破片进行表征，FE-SPH自适应方法可以直接获取大质量破片信息，但比SPH方法的求解效率低。
- 数值模拟方法 /
- SPG /
- SPH /
- 二次破片 /
- 侵彻
Abstract: In order to improve the quantitative characterization of the penetration process of tungsten alloy projectile into the target, the numerical methods such as FEM (finite element method), SPG (smoothed particle Galerkin), SPH (smoothed particle hydrodynamics), and FE-SPH (finite element-smoothed particle hydrodynamics) adaptive simulation methods were employed to simulate the penetration of tungsten alloy projectiles into Q235A steel targets. Based on numerical simulations, a comparison was made of the advantages and disadvantages of the four numerical simulation methods for calculating the residual velocity of the projectile after penetrating the target, the perforation diameter of the target, and the distribution of secondary fragments by the projectile penetration. The results show that, for calculating the residual velocity of the projectile, FEM and FE-SPH adaptive methods strictly rely on the selection of failure criteria and corresponding parameters, as FEM employs an element erosion algorithm to model material failure, while SPG method, as it does not require adjusting the failure parameters in bond failure mode, can obtain relatively accurate calculations; for predicting perforation diameter, FEM and FE-SPH adaptive methods accurately represent material boundaries and perforation morphology, although the perforation diameter varies significantly under different failure criteria, while the SPG method can accurately predict the perforation diameter of target plates due to its insensitive to failure parameters; for analzing secondary fragments generation and distribution, both FE-SPH adaptive and SPH methods effectively characterize these phenomena, while the FE-SPH adaptive method provides detailed information on large fragments, it is less computationally efficient than the SPH method.
- finite element method (FEM) /
- smoothed particle Galerkin (SPG) /
- smoothed particle hydrodynamics (SPH) /
- secondary fragments /
- penetration

HTML全文

图 1 试验布置示意图

Figure 1. Sketch of the experimental setup

下载: 全尺寸图片幻灯片

图 2 靶板的出入口形貌

Figure 2. Entry and exit features of the targets

下载: 全尺寸图片幻灯片

图 3 FEM方法数值模拟模型

Figure 3. Numerical simulation model of FEM

下载: 全尺寸图片幻灯片

图 4 SPG方法数值模拟模型

Figure 4. Numerical simulation model of SPG method

下载: 全尺寸图片幻灯片

图 5 FEM-SPH固定耦合方法数值模拟模型

Figure 5. Numerical simulation model of FEM-SPH fixed coupling method

下载: 全尺寸图片幻灯片

图 6 弹丸侵彻6 mm厚Q235钢靶板剩余速度试验值与模拟值的对比

Figure 6. Comparison of the experimental and numerical residual velocity of projectile in 6 mm Q235 steel targets penetration tests

下载: 全尺寸图片幻灯片

图 7 弹丸侵彻4 mm厚Q235钢靶板剩余速度试验值与模拟值的对比

Figure 7. Comparison of the experimental and numerical residual velocity of projectile in 4 mm Q235 steel targets penetration tests

下载: 全尺寸图片幻灯片

图 8 失效参数对剩余速度的影响（v₀=619.2 m/s，h=6 mm）

Figure 8. Effect of failure parameters on residual velocity (v₀=619.2 m/s，h=6 mm)

下载: 全尺寸图片幻灯片

图 9 弹丸剩余速度随有效塑性应变的变化情况（v₀=1204.8 m/s，h=4 mm）

Figure 9. Variation of residual velocity of projectile with effective plastic strain (v₀=1204.8 m/s，h=4 mm)

下载: 全尺寸图片幻灯片

图 10 弹丸侵彻6 mm厚Q235钢靶板剩余速度试验值与模拟值对比

Figure 10. Comparison of the experimental and numerical residual velocity of projectile in 6mm Q235 steel targets penetration tests

下载: 全尺寸图片幻灯片

图 11 弹丸侵彻4 mm厚Q235靶板剩余速度试验值与模拟值对比

Figure 11. Comparison of the experimental and numerical residual velocity of projectile in 4 mm Q235 steel targets penetration tests

下载: 全尺寸图片幻灯片

图 12 不同失效准则下弹丸剩余速度随失效参数变化情况

Figure 12. Variation of projectile residual velocity with failure parameters under different failure criteria

下载: 全尺寸图片幻灯片

图 13 靶板穿孔形貌特征

Figure 13. Perforation features of target plate

下载: 全尺寸图片幻灯片

图 14 弹丸侵彻6 mm厚Q235钢靶板穿孔直径试验值与模拟值对比

Figure 14. Comparison of test and simulation values of perforation diameter of 6 mm Q235 steel target plate penetrated by projectile

下载: 全尺寸图片幻灯片

图 15 弹丸侵彻4 mm厚Q235靶板穿孔直径试验值与模拟值对比

Figure 15. Comparison of test and simulation values of perforation diameter of 4 mm Q235 target plate penetrated by projectile

下载: 全尺寸图片幻灯片

图 16 靶板穿孔直径随有效塑性应变的变化情况(v₀=751.9 m/s，h=6 mm)

Figure 16. Change of perforation diameter of target plate with effective plastic strain(v₀=751.9 m/s，h=6 mm)

下载: 全尺寸图片幻灯片

图 17 残余弹丸及破片对后效靶的毁伤作用

Figure 17. Dmage effect of residual projectiles and fragments to witness target

下载: 全尺寸图片幻灯片

图 18 二次破片对验证靶的毁伤情况

Figure 18. Damage effect of secondary fragments on witness target

下载: 全尺寸图片幻灯片

图 19 v₀ = 1197.6 m/s、h = 6 mm时二次破片云的形貌

Figure 19. Morphology of secondary fragments at v₀ = 1197.6 m/s，h = 6 mm

下载: 全尺寸图片幻灯片

图 20 v₀ = 1190.5 m/s、h = 4 mm时二次破片云的形貌

Figure 20. Morphology of secondary fragments at v₀ = 1190.5 m/s，h = 4 mm

下载: 全尺寸图片幻灯片

图 21 二次破片在虚拟验证靶上的分布情况（v₀ = 1197.6 m/s，h = 6 mm）

Figure 21. Distribution of secondary fragments on the witness target (v₀ = 1197.6 m/s，h = 6 mm)

下载: 全尺寸图片幻灯片

图 22 二次破片在虚拟验证靶上的分布情况（v₀ = 1090.5 m/s，h = 4 mm）

Figure 22. Distribution of secondary fragments on the witness target (v₀ = 1090.5 m/s，h = 4 mm)

下载: 全尺寸图片幻灯片

表 1 钨合金弹丸侵彻不同厚度Q235钢板的试验结果

Table 1. Experimental results of tungsten alloy projectile penetration into Q235 steel plate with different thickness

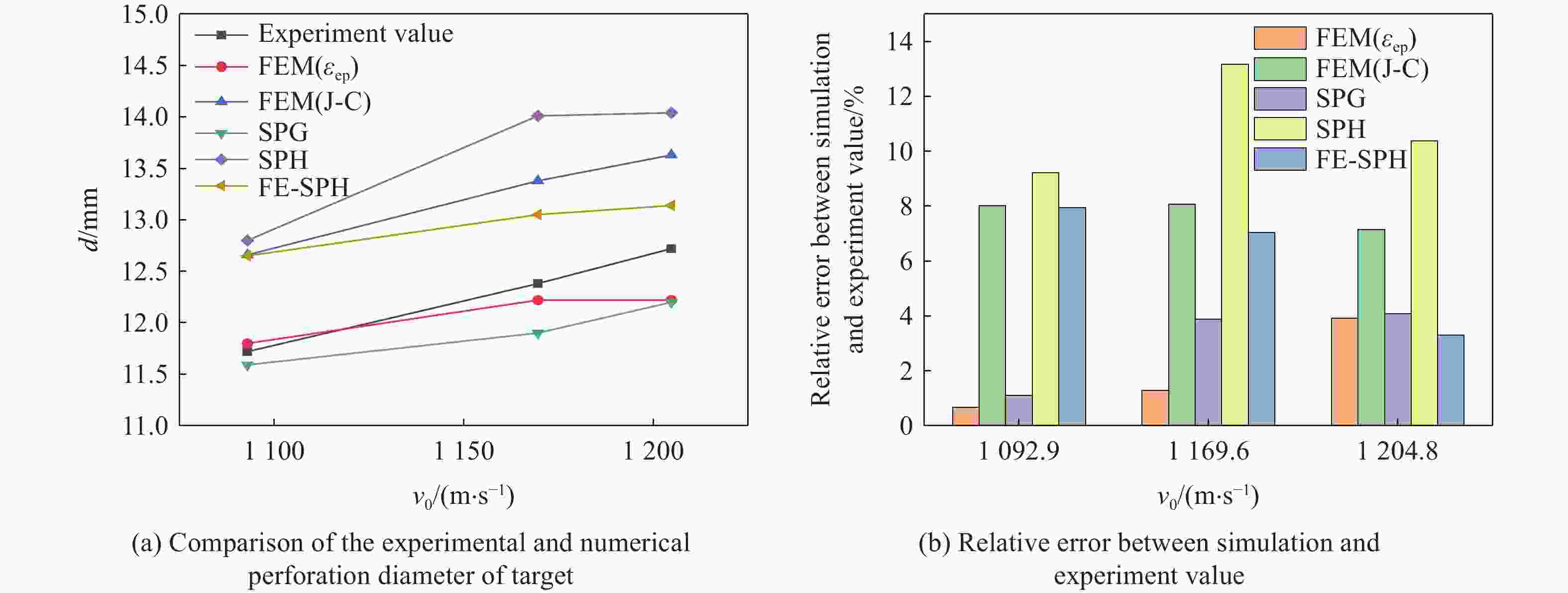
试验序号	靶板厚度/mm	着靶速度/(m·s⁻¹)	剩余速度/(m·s⁻¹)	穿孔孔径/mm
1	4	1092.9	888.9	11.72
2	4	1169.6	952.4	12.38
3	4	1204.8	980.4	12.72
4	4	1190.5	—	12.58
5	6	1197.6	—	12.95
6	6	1197.6	865.8	13.00
7	6	751.9	489.0	9.95
8	6	619.2	346.6	9.70
注: (1)“—”表示增加了验证靶，未对剩余速度进行测量；(2)穿孔孔径为靶板入口直径与出口直径的平均值。

下载: 导出CSV

表 2 数值模拟中材料的失效准则及失效参数

Table 2. Material failure criteria and parameters for numerical simulation

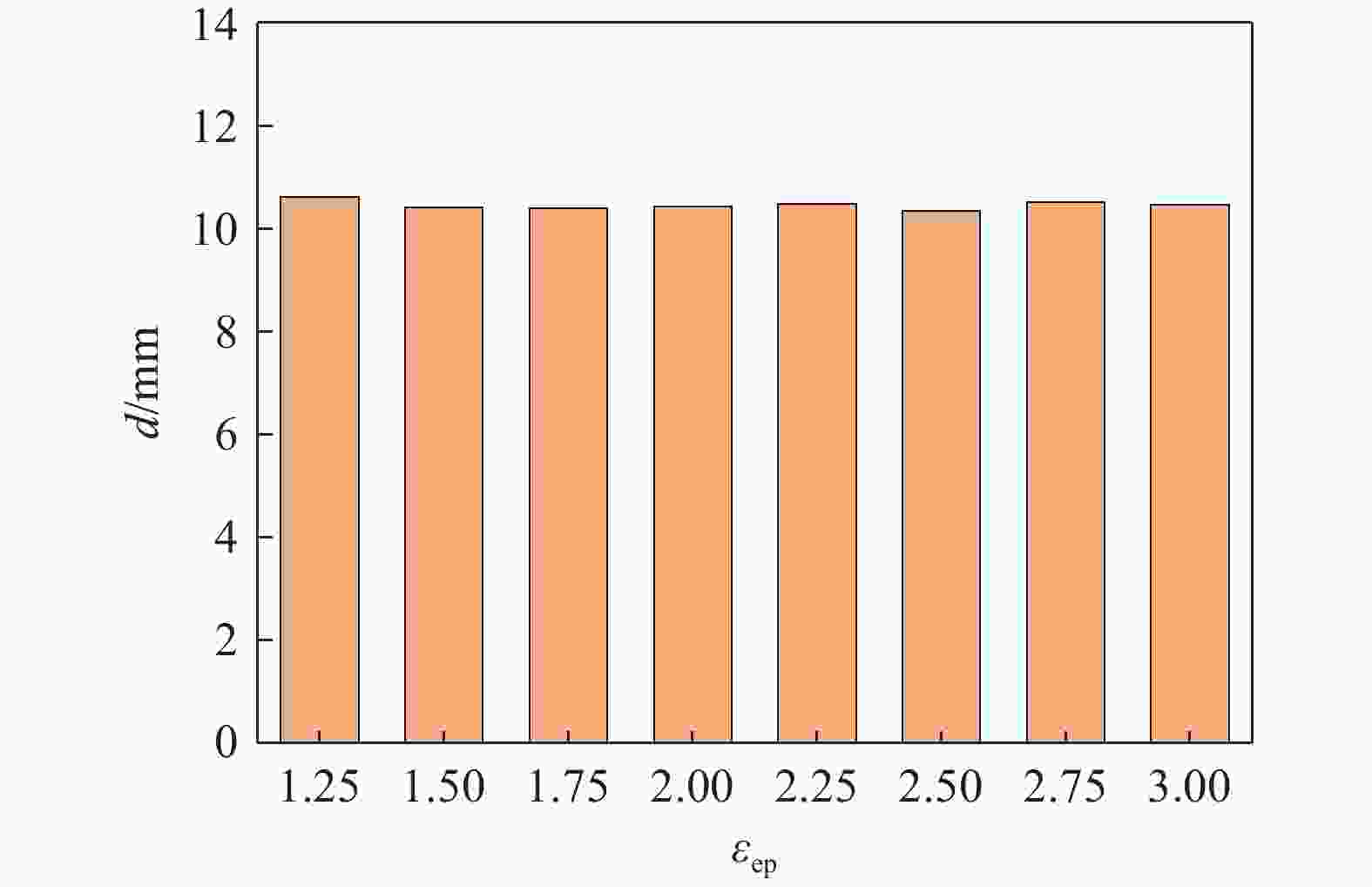
数值模拟方法	失效准则	失效参数
数值模拟方法	失效准则	弹丸材料	靶板材料
FEM	有效塑性应变（ε_ep）	1.6	1.36
FEM	Johnson-Cook失效准则	—	d₁=0.3、d₂=0.9、d₃=2.8
SPG	有效塑性应变	F_s=1.6	F_s=1.36
SPH	最大拉应力	—	P₁= 4 GPa
FE-SPH	J-C失效+最大拉应力	—	d₁=0.3、d₂=0.9、d₃=2.8 P₁ =4 GPa
注：弹丸材料均采用有效塑性应变失效准则，有效塑性应变取值为1.6。

下载: 导出CSV

表 3 二次破片在验证靶上的穿孔数与弹坑数

Table 3. Numbers of penetrations and craters on witness target caused by secondary fragments

靶板厚度/mm
靶板厚度/mm	穿孔数量	弹坑数量
4	9	10
6	10	9

下载: 导出CSV

表 4 不同数值模拟方法得到的二次破片在验证靶上的穿孔数量对比

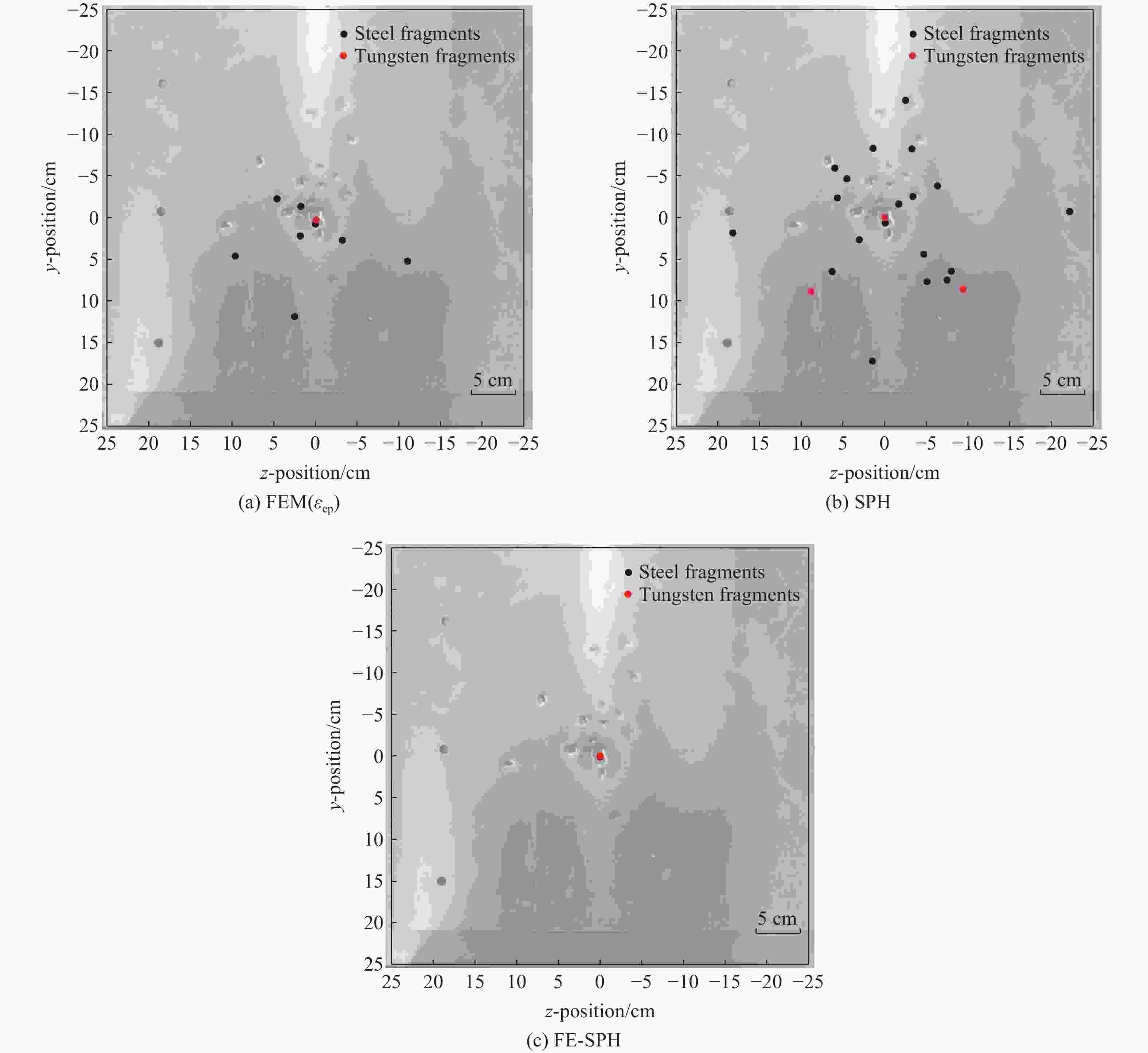
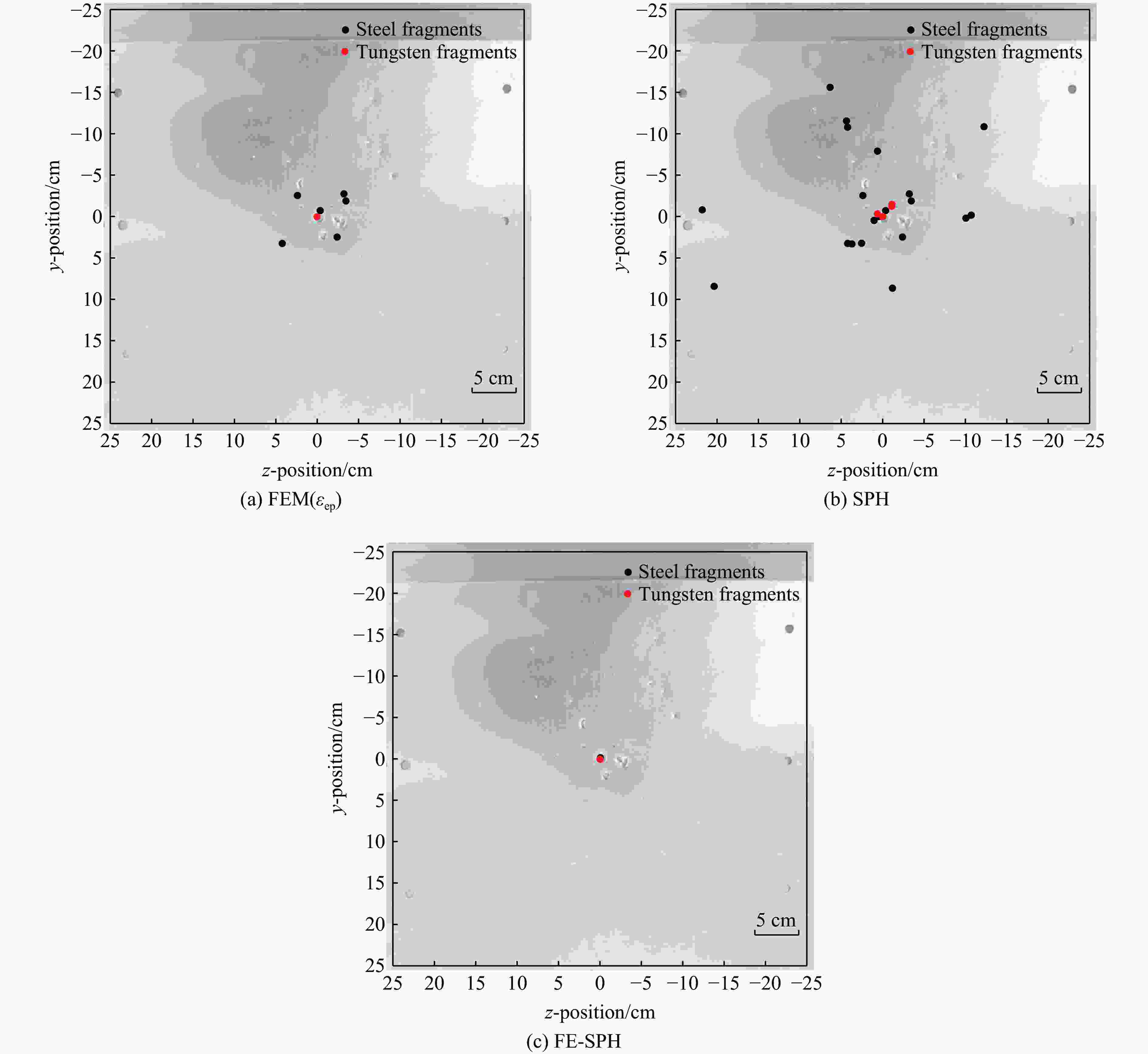
Table 4. Comparison of the number of perforations on witness target by secondary fragments obtained from various numerical simulation methods

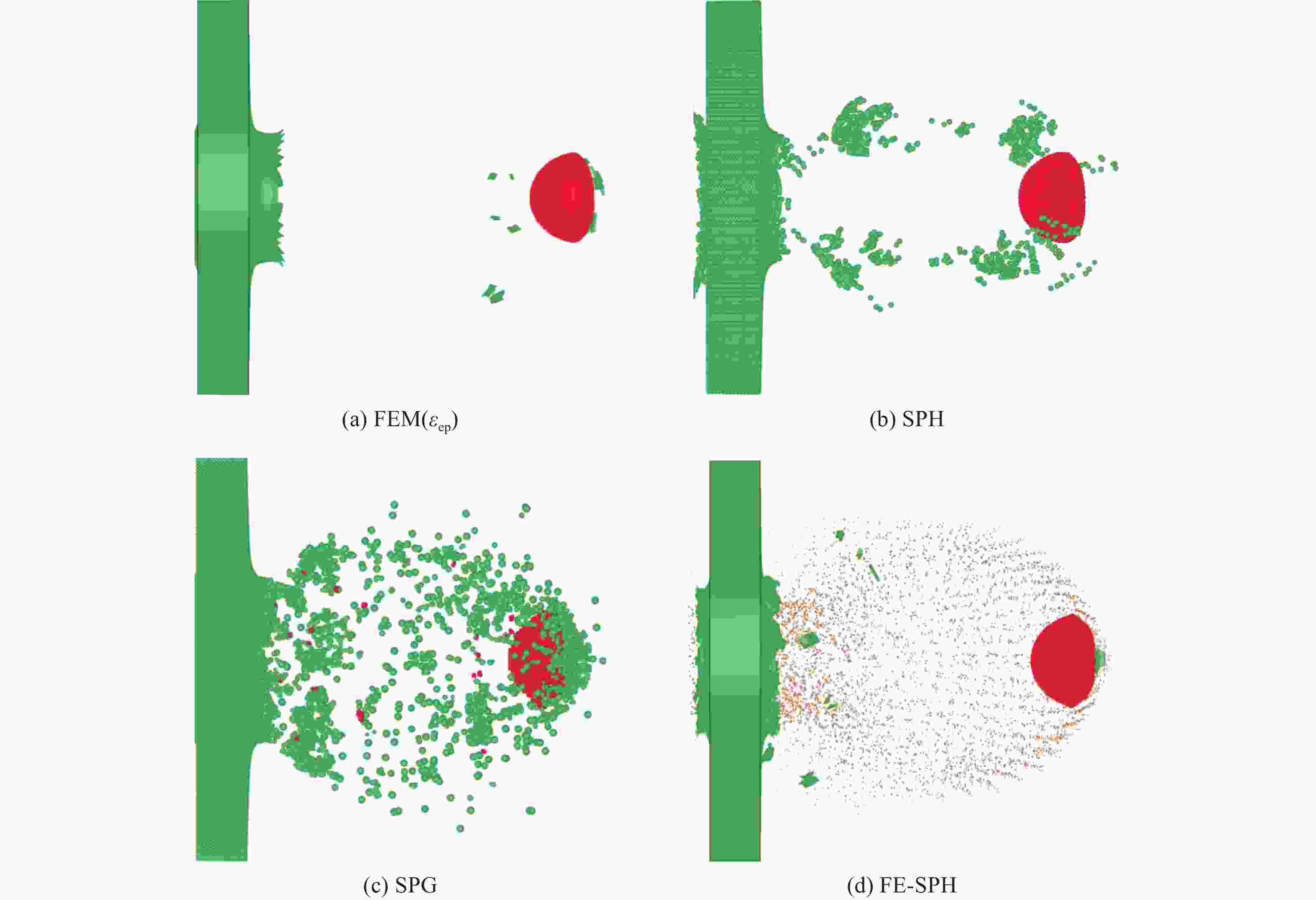
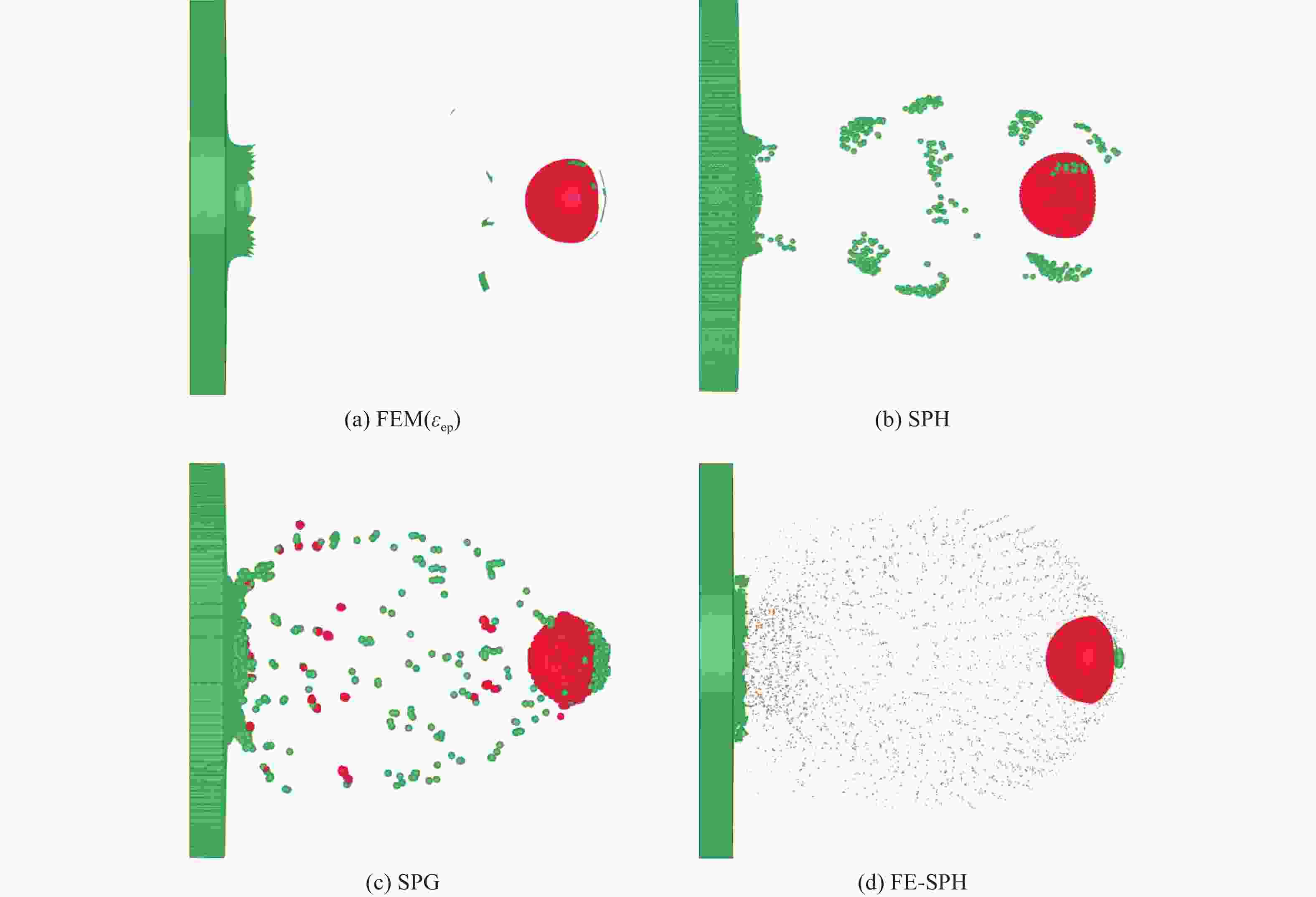
靶板厚度/mm	试验结果		模拟计算结果（穿孔数）
靶板厚度/mm	穿孔数	弹坑数	FEM	SPH	FE-SPH
4	9	10	7	20	2
6	10	9	9	24	3

下载: 导出CSV

表 5 不同数值模拟方法的计算时间

Table 5. Computational time of different numerical simulation methods

数值模拟方法	FEM(ε_ep)	FEM(J-C)	SPG	SPH	FE-SPH
计算时间（100 μs时刻）	8 min 51 s	44 min 17 s	2 h 20 min 17 s	2 h 14 min 20 s	6 h 2 min 46 s

下载: 导出CSV

参考文献(24)

[1]	何杨, 高旭东, 董晓亮. 某陶瓷/钢复合装甲抗大质量破片侵彻能力研究 [J]. 振动与冲击, 2022, 41(13): 96–102. DOI: 10.13465/j.cnki.jvs.2022.13.013. HE Y, GAO X D, DONG X L. Anti-penetration ability of a certain ceramic/steel composite armor against high mass fragments [J]. Journal of Vibration and Shock, 2022, 41(13): 96–102. DOI: 10.13465/j.cnki.jvs.2022.13.013.
[2]	陈艳丹, 陈兴, 卢永刚, 等. 球形弹丸高速冲击IN718合金板的变形与破坏模式 [J]. 爆炸与冲击, 2024, 44(2): 023301. DOI: 10.11883/bzycj-2023-0071. CHEN Y D, CHEN X, LU Y G, et al. Deformation and failure modes of IN718 alloy plateimpacted by spherical projectile at high velocity [J]. Explosion and Shock Waves, 2024, 44(2): 023301. DOI: 10.11883/bzycj-2023-0071.
[3]	刘铁磊, 徐豫新, 王晓锋, 等. 钨合金球形破片侵彻低碳钢的弹道极限速度计算模型 [J]. 兵工学报, 2022, 43(4): 768–779. DOI: 10.12382/bgxb.2021.0448. LIU T L, XU Y X, WANG X F, et al. Ballistic limit calculation model of tungsten alloy spherical fragments penetrating into low carbon steel plate [J]. Acta Armamentarii, 2022, 43(4): 768–779. DOI: 10.12382/bgxb.2021.0448.
[4]	王逸凡, 李永鹏, 徐豫新, 等. 钨球对碳纤维增强复合材料包覆碳化硼陶瓷侵彻效应 [J]. 兵工学报, 2024, 45(8): 2487–2496. DOI: 10.12382/bgxb.2023.1083. WANG Y F, LI Y P, XU Y X, et al. Penetration effect of tungsten alloy spherical projectile on CFRP-coated B₄C ceramics [J]. Acta Armamentarii, 2024, 45(8): 2487–2496. DOI: 10.12382/bgxb.2023.1083.
[5]	张钰龙, 郑宾, 郭华玲, 等. 球形钨破片侵彻钢靶毁伤效应研究 [J]. 兵器装备工程学报, 2020, 41(5): 32–36. DOI: 10.11809/bqzbgexb2020.05.007. ZHANG Y L, ZHENG B, GUO H L, et al. Study on damage effect of spherical tungsten fragments penetrating steel targets [J]. Journal of Ordnance Equipment Engineering, 2020, 41(5): 32–36. DOI: 10.11809/bqzbgexb2020.05.007.
[6]	包阔, 张先锋, 谈梦婷, 等. 子弹撞击碳化硼陶瓷复合靶试验与数值模拟研究 [J]. 爆炸与冲击, 2019, 39(12): 123102. DOI: 10.11883/bzycj-2018-0462. BAO K, ZHANG X F, TAN M T, et al. Ballistic test and numerical simulation on penetration of a boron-carbide-ceramic composite target by a bullet [J]. Explosion and Shock Waves, 2019, 39(12): 123102. DOI: 10.11883/bzycj-2018-0462.
[7]	马铭辉, 武一丁, 王晓东, 等. 多孔钛合金夹芯层陶瓷/UHMWPE复合结构的抗侵彻性能 [J]. 爆炸与冲击, 2024, 44(4): 041001. DOI: 10.11883/bzycj-2023-0375. MA M H, WU Y D, WANG X D, et al. Penetration resistance of ceramic/UHMWPE composite structures with porous titanium alloy sandwich layer [J]. Explosion and Shock Waves, 2024, 44(4): 041001. DOI: 10.11883/bzycj-2023-0375.
[8]	周楠, 王金相, 王小绪, 等. 球形弹丸作用下钢/铝爆炸复合靶的抗侵彻性能 [J]. 爆炸与冲击, 2011, 31(5): 497–503. DOI: 10.11883/1001-1455(2011)05-0497-07. ZHOU N, WANG J X, WANG X X, et al. Anti-penetration performances of explosively welded steel/aluminium plates impacted by spherical projectiles [J]. Explosion and Shock Waves, 2011, 31(5): 497–503. DOI: 10.11883/1001-1455(2011)05-0497-07.
[9]	徐豫新, 任杰, 王树山. 钨球正撞击下低碳钢板的极限贯穿厚度研究 [J]. 北京理工大学学报, 2017, 37(6): 551–556. DOI: 10.15918/j.tbit1001-0645.2017.06.001. XU Y X, REN J, WANG S S. Research on perforation limit thickness of low carbon steel plates impacted normally by tungsten spheres [J]. Transactions of Beijing Institute of Technology, 2017, 37(6): 551–556. DOI: 10.15918/j.tbit1001-0645.2017.06.001.
[10]	邸德宁, 陈小伟. 碎片云SPH方法数值模拟中的材料失效模型 [J]. 爆炸与冲击, 2018, 38(5): 948–956. DOI: 10.11883/bzycj-2017-0328. DI D N, CHEN X W. Material failure models in SPH simulation of debris cloud [J]. Explosion and Shock Waves, 2018, 38(5): 948–956. DOI: 10.11883/bzycj-2017-0328.
[11]	WEN K, CHEN X W, DI D N. Modeling on the shock wave in spheres hypervelocity impact on flat plates [J]. Defence Technology, 2019, 15(4): 457–466. DOI: 10.1016/j.dt.2019.01.006.
[12]	WEN K, CHEN X W. Influence of the impedance gradient on the debris cloud produced by hypervelocity impact [J]. International Journal of Impact Engineering, 2022, 159: 104034. DOI: 10.1016/j.ijimpeng.2021.104034.
[13]	WEN K, CHEN X W. Analysis of the stress wave and rarefaction wave produced by hypervelocity impact of sphere onto thin plate [J]. Defence Technology, 2020, 16(5): 969–979. DOI: 10.1016/j.dt.2019.11.017.
[14]	PIEKUTOWSKI A J. Formation and description of debris cloud produced by hypervelocity impact: NASA CR-4707 [R]. NASA: Marshall Space Flight Center, 1996.
[15]	HE Q G, CHEN X W, CHEN J F. Finite element-smoothed particle hydrodynamics adaptive method in simulating debris cloud [J]. Acta Astronautica, 2020, 175: 99–117. DOI: 10.1016/j.actaastro.2020.05.056.
[16]	HE Q G, CHEN X W. Simulation method of debris cloud from fiber-reinforced composite shield under hypervelocity impact [J]. Acta Astronautica, 2023, 204: 402–417. DOI: 10.1016/j.actaastro.2023.01.008.
[17]	YIN X, LI Q H, CHEN B K, et al. An improved calibration of Karagozian & Case concrete/cementitious model for strain-hardening fibre-reinforced cementitious composites under explosion and penetration loadings [J]. Cement and Concrete Composites, 2023, 137: 104911. DOI: 10.1016/j.cemconcomp.2022.104911.
[18]	WU Y C, WU C T. Simulation of impact penetration and perforation of metal targets using the smoothed particle Galerkin method [J]. Journal of Engineering Mechanics, 2018, 144(8): 04018057. DOI: 10.1061/(ASCE)EM.1943-7889.0001470.
[19]	陈刚, 陈小伟, 陈忠富, 等. A3钢钝头弹撞击45钢板破坏模式的数值分析 [J]. 爆炸与冲击, 2007, 27(5): 390–397. DOI: 10.11883/1001-1455(2007)05-0390-08. CHEN G, CHEN X W, CHEN Z F, et al. Simulations of A3 steel blunt projectiles impacting 45 steel plates [J]. Explosion and Shock Waves, 2007, 27(5): 390–397. DOI: 10.11883/1001-1455(2007)05-0390-08.
[20]	SILLING S A, ASKARI E. A meshfree method based on the peridynamic model of solid mechanics [J]. Computers & Structures, 2005, 83(17/18): 1526–1535. DOI: 10.1016/j.compstruc.2004.11.026.
[21]	WU C T, REN B. A stabilized non-ordinary state-based peridynamics for the nonlocal ductile material failure analysis in metal machining process [J]. Computer Methods in Applied Mechanics and Engineering, 2015, 291: 197–215. DOI: 10.1016/j.cma.2015.03.003.
[22]	WU C T, BUI T Q, WU Y C, et al. Numerical and experimental validation of a particle Galerkin method for metal grinding simulation [J]. Computational Mechanics, 2018, 61(3): 365–383. DOI: 10.1007/s00466-017-1456-6.
[23]	黄长强, 朱鹤松. 球形破片对靶板极限穿透速度公式的建立 [J]. 弹箭与制导学报, 1993, 13(2): 58–61.
[24]	郭锐, 陈佑明, 杨贵涛, 等. 一种基于LS-DYNA的SPH算法破片识别方法: CN115099120A [P]. 2022-09-23. GUO R, CHEN Y M, YANG G T, et al. SPH algorithm fragment identification method based on LS-DYNA: CN115099120A [P]. 2022-09-23.