弹体侵彻钢筋混凝土遮弹层的阻力方程

王武; 杨军; 王安宝; 李胜杰

doi:10.11883/bzycj-2024-0217

弹体侵彻钢筋混凝土遮弹层的阻力方程

doi: 10.11883/bzycj-2024-0217

王武^{1, 2,},
杨军^1, ,,
王安宝²,
李胜杰¹

1.
清华大学土木工程系, 北京 100084
2.
军事科学院国防工程研究院, 北京 100036

详细信息

作者简介:
王　武（1985－　），男，博士研究生，工程师，w-wang21@mails.tsinghua.edu.cn

通讯作者:
杨　军（1974－　），男，博士，研究员，junyang@tsinghua.edu.cn

中图分类号: O385
计量
- 文章访问数: 110
- HTML全文浏览量: 11
- PDF下载量: 51
- 被引次数: 0
出版历程
- 收稿日期: 2024-07-02
- 修回日期: 2024-09-15
- 网络出版日期: 2024-09-19

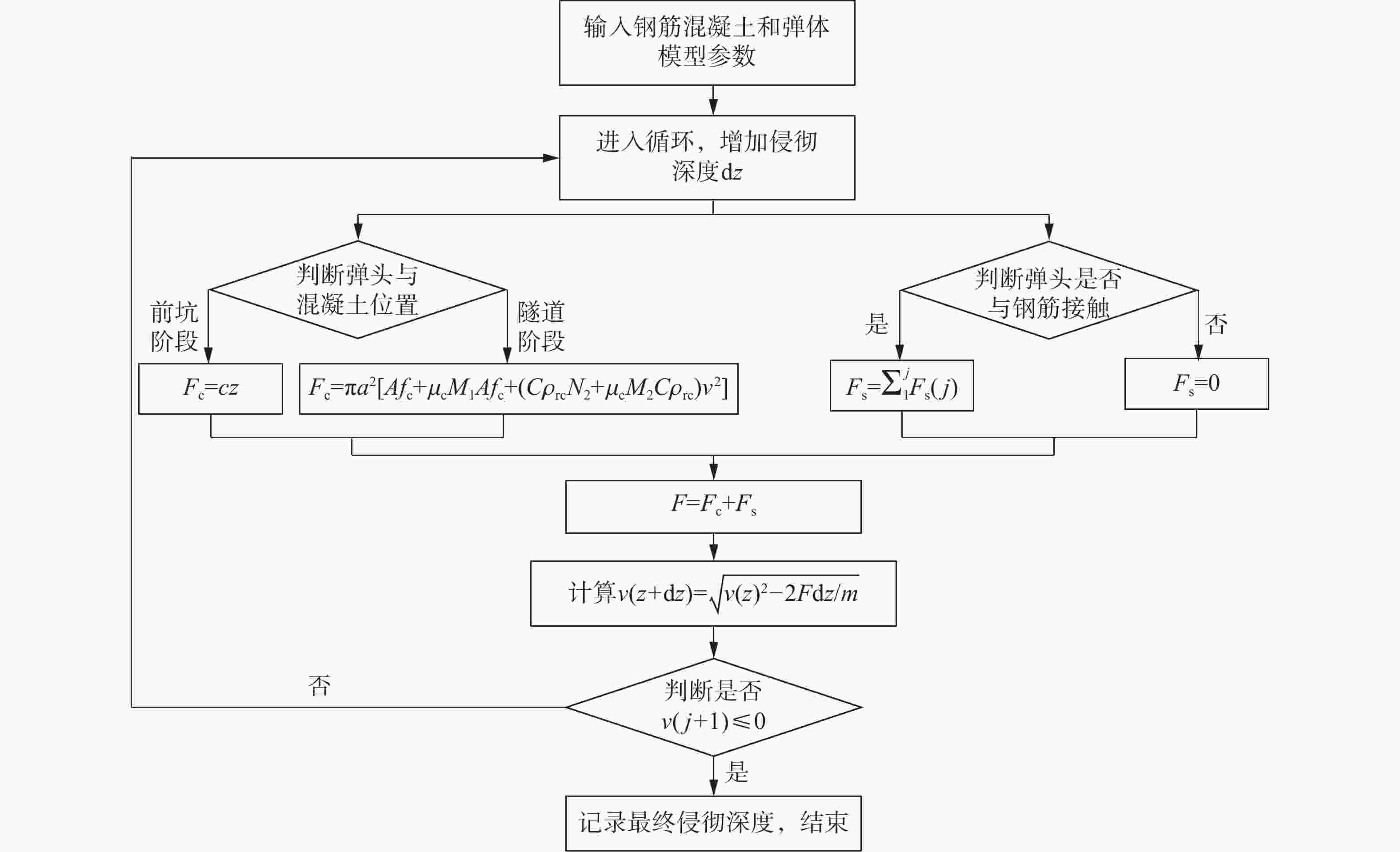
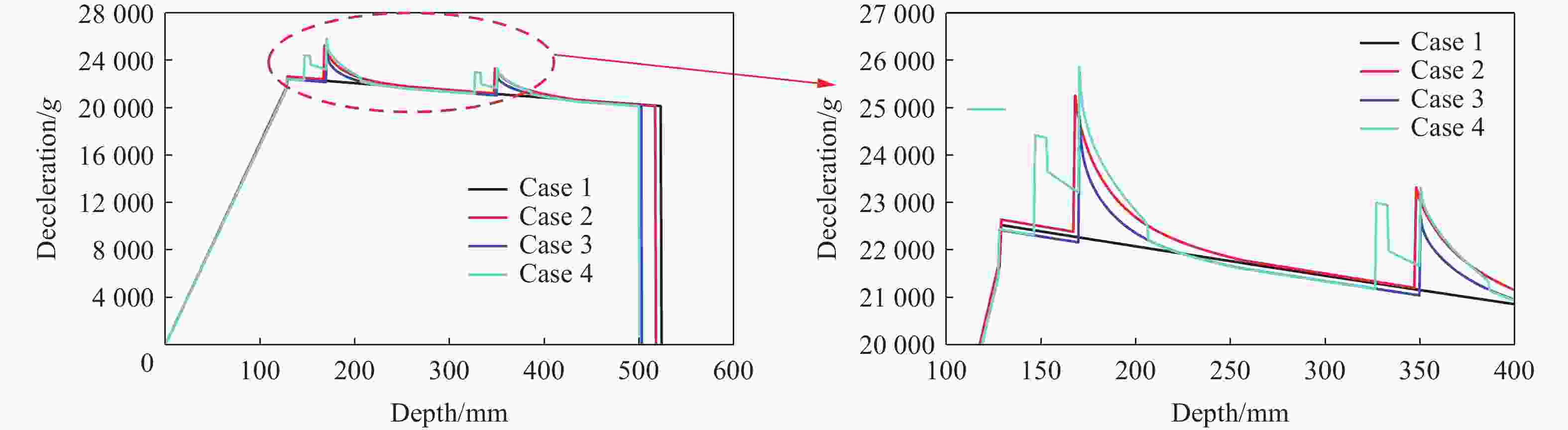
Resistance equation of projectile penetrating into reinforced concrete shield

WANG Wu^{1, 2
,},
YANG Jun^{1
, ,},
WANG Anbao²,
LI Shengjie¹

1.
Department of Civil Engineering, Tsinghua University, Beijing 100084, China
2.
Institute of Defense Engineering, AMS, PLA, Beijing 100036, China

摘要

摘要: 为研究弹体在侵彻钢筋混凝土受到阻力的问题，分析了现有钢筋有限长度固支梁理论模型局限，根据钢筋屈服准则研究和耗能分析，提出了弹体直接命中钢筋剪切-塑性铰链模型，以及弹体与钢筋侧面接触时的塑性弦模型，通过耗能分析得到了弹体直接阻力函数；以空腔膨胀理论模型为基础，根据弹体侵彻深度经验公式计算结果，得到了钢筋间接影响下混凝土阻力方程。通过与已有试验数据对比，验证了理论模型的合理性。通过分析钢筋屈服强度、直径、网眼尺寸等配筋方式，以及弹体命中部位对遮弹层抗侵彻性能的影响，给出了遮弹层配筋设计建议：相邻两层钢筋网错孔设置；钢筋网眼与弹体直径比值宜设为0.5～0.8；应结合钢筋极限塑性应变进行高强钢筋选择。
- 钢筋混凝土 /
- 侵彻阻力 /
- 理论模型 /
- 配筋设计
Abstract: To study the penetration resistance to the projectile by the reinforced concrete, the mechanical response of reinforcing bars under the dynamic constraint of both the projectile and concrete was analysed and the limitation of existing finite-length rigid beam models have been obtained. Based on this foundation, a shear-plastic hinge model was used to analyze the case of a projectile directly hitting the reinforcing bars, and a plastic string model was used to analyze the case of a projectile colliding with the side of the reinforcing bars, resulting in a more accurate equation for penetration resistance. In the shear plastic hinge model, stress analysis was performed based on the shear sliding of the reinforcing bar before fracture, and energy dissipation was calculated based on the deformation of the plastic hinge after the reinforcing bar fractures. In the plastic string model, the yield criterion of reinforcing bars under the combined action of bending moment and axial force was analyzed, and the plastic energy dissipation equations for reinforcing bar tension and bending were established. At the same time, the influence of changes in reinforcing bar kinetic energy was considered. Based on the theoretical model of cavity expansion and the empirical formula for the depth of projectile penetration, the concrete resistance equation under the indirect influence of steel reinforcement was obtained. By comparing with existing experimental data, the rationality of the theoretical models was verified. By analyzing the yield strength, diameter, mesh size of reinforcing bars, as well as the impact location of projectile, suggestions for the reinforcement design of the bulletproof layer were given. The adjacent two layers of reinforcing bars mesh should be staggered. The ratio of steel mesh to projectile diameter should be set between 0.5 and 0.8. It is not advisable to simply pursue high-strength reinforcing bars, and the ultimate plastic strain of reinforcing bars should also be considered as an important factor.
- reinforced concrete /
- penetration resistance /
- theoretical model /
- reinforcement design

HTML全文

图 1 弹体与钢筋接触方式^[15]

Figure 1. Contact method between projectile and reinforcing bar^[15]

下载: 全尺寸图片幻灯片

图 2 钢筋受力示意图

Figure 2. Schematic diagram of reinforcing bar under dynamic load

下载: 全尺寸图片幻灯片

图 3 尖卵头刚性弹剖面示意图

Figure 3. Schematic diagram of oval shaped projectile

下载: 全尺寸图片幻灯片

图 4 塑性铰等效长度

Figure 4. Equivalent length of plastic hinge

下载: 全尺寸图片幻灯片

图 5 塑性铰链变形示意图

Figure 5. Schematic diagram of plastic hinge deformation

下载: 全尺寸图片幻灯片

图 6 钢筋受弯矩作用屈服时横截面应力分布

Figure 6. Cross section stress distribution of reinforcing bar under bending moment action

下载: 全尺寸图片幻灯片

图 7 钢筋受弯矩和轴力共同作用屈服时横截面应力分布

Figure 7. Cross section stress distribution of reinforcing bar under combined bending moment and axial force

下载: 全尺寸图片幻灯片

图 8 弯矩-轴力共同作用下钢筋屈服面

Figure 8. Yield surface of reinforcing bar under the combined action of bending moment and axial force

下载: 全尺寸图片幻灯片

图 9 钢筋塑性变形区示意图

Figure 9. Schematic of plastic deformation zone of reinforcing bar

下载: 全尺寸图片幻灯片

图 10 弹体侵彻计算流程图

Figure 10. Flow chart of projectile penetration calculation

下载: 全尺寸图片幻灯片

图 11 侵彻试验后部分靶板及钢筋破坏形态^[30]

Figure 11. Partial target plate and reinforcing bars failure morphology after penetration test^[30]

下载: 全尺寸图片幻灯片

图 12 弹体减加速度计算结果

Figure 12. Calculation results of projectile deceleration

下载: 全尺寸图片幻灯片

图 13 单层钢筋网耗能计算结果

Figure 13. Calculation results of energy consumption for single-layer reinforcing bar mesh

下载: 全尺寸图片幻灯片

表 1 钢筋混凝土靶侵彻试验工况及结果

Table 1. Test conditions and results of reinforced concrete target penetration test

靶板编号	计划撞击点位置	配筋方式/mm	弹体质量/g	弹体初速度/(m·s⁻¹)	侵彻深度/mm
靶板编号	计划撞击点位置	配筋方式/mm	弹体质量/g	弹体初速度/(m·s⁻¹)	试验结果^[30]	理论计算结果	相对误差/%
#1	网眼中心	$ \varnothing $10@75	4914	439	568	523	7.92
#2	钢筋交叉点	$ \varnothing $10@75	4920	439	546	503	7.88
#3	网眼中心	$ \varnothing $6.5@30	4968	430	552	517	6.34
#4	钢筋交叉点	$ \varnothing $6.5@30	4962	431	—	501	—

下载: 导出CSV

表 2 弹体侵彻钢筋混凝土靶部分影响参数

Table 2. Impact parameters of projectile penetration into reinforced concrete targets

γ_vol/%	2b/mm	s_h/mm	s_h/2a	γ_vol/%	2b/mm	s_h/mm	s_h/mm	γ_vol/%	2b/mm	s_h/mm	s_h/mm
4	10	26.18	0.17	5	12	30.16	0.2	6	14	34.21	0.23
	12	37.7	0.25		14	41.05	0.27		16	44.68	0.3
	14	51.31	0.34		16	53.62	0.36		18	56.55	0.38
	16	67.02	0.45		18	67.86	0.45		20	69.81	0.47
	18	84.82	0.57		20	83.78	0.56		22	84.47	0.56
	20	104.72	0.7		22	101.37	0.68		24	100.53	0.67
	22	126.71	0.84		24	120.64	0.8		26	117.98	0.79
	24	150.8	1.01		26	141.58	0.94		28	136.83	0.91
注：$ {\gamma }_{\text{vol}} $为体积配筋率，2b为钢筋直径，s_h为钢筋网眼大小。

下载: 导出CSV

参考文献(30)

[1]	KENNEDY R P. A review of procedures for the analysis and design of concrete structures to resist missile impact effects [J]. Nuclear Engineering and Design, 1976, 37(2): 183–203. DOI: 10.1016/0029-5493(76)90015-7.
[2]	LI Q M, REID S R, WEN H M, et al. Local impact effects of hard missiles on concrete targets [J]. International Journal of Impact Engineering, 2005, 32(1/2/3/4): 224–284. DOI: 10.1016/j.ijimpeng.2005.04.005.
[3]	RIERA J D. Penetration, scabbing and perforation of concrete structures hit by solid missiles [J]. Nuclear Engineering and Design, 1989, 115(1): 121–131. DOI: 10.1016/0029-5493(89)90265-3.
[4]	邓勇军, 陈小伟, 钟卫洲, 等. 弹体正侵彻钢筋混凝土靶的试验及数值模拟研究 [J]. 爆炸与冲击, 2020, 40(2): 023101. DOI: 10.11883/bzycj-2019-0001. DENG Y J, CHEN X W, ZHONG W Z, et al. Experimental and numerical study on normal penetration of a projectile into a reinforced concrete target [J]. Explosion and Shock Waves, 2020, 40(2): 023101. DOI: 10.11883/bzycj-2019-0001.
[5]	LUK V K, FORRESTAL M J. Penetration into semi-infinite reinforced-concrete targets with spherical and ogival nose projectiles [J]. International Journal of Impact Engineering, 1987, 6(4): 291–301. DOI: 10.1016/0734-743X(87)90096-0.
[6]	BARR P. Guidelines for the design and assessment of concrete structures subjected to impact: SRD-R-439-Issue-2 [R]. London: HMSO, 1988.
[7]	NDRC. Effects of impact and explosion: Summary Technical Report of Division 2, Vol. 1 [R]. Washington DC: National Defense Research Committee, 1946.
[8]	BERRIAUD C, SOKOLOVSKY A, GUERAUD R, et al. Local behaviour of reinforced concrete walls under missile impact [J]. Nuclear Engineering & Design, 1978, 45(2): 457–469. DOI: 10.1016/0029-5493(78)90235-2.
[9]	DANCYGIER A N. Effect of reinforcement ratio on the resistance of reinforced concrete to hard projectile impact [J]. Nuclear Engineering & Design, 1997, 172(1/2): 233–245. DOI: 10.1016/S0029-5493(97)00055-1.
[10]	CHEN X W, LI X L, HUANG F L, et al. Normal Perforation of reinforced concrete target by rigid projectile [J]. International Journal of Impact Engineering, 2008, 35(10): 1119–1129. DOI: 10.1016/j.ijimpeng.2008.01.002.
[11]	GRISARO H, DANCYGIER A N. A modified energy method to assess the residual velocity of non-deforming projectiles that perforate concrete barriers [J]. International Journal of Protective Structures, 2014, 5(3): 307–321. DOI: 10.1260/2041-4196.5.3.307.
[12]	XU X Z, MA T B, NING J G. Failure mechanism of reinforced concrete subjected to projectile impact loading [J]. Engineering Failure Analysis, 2019, 96: 468–483. DOI: 10.1016/j.engfailanal.2018.11.006.
[13]	DENG Y J, CHEN X W, SONG W J. Dynamic cavity-expansion penetration model of elastic-cracked-crushed response for reinforced-concrete targets [J]. International Journal of Impact Engineering, 2021, 157: 103981. DOI: 10.1016/j.ijimpeng.2021.103981.
[14]	LEE S, KIM C, YU Y, et al. Effect of reinforcing steel on the impact resistance of reinforced concrete panel subjected to hard-projectile impact [J]. International Journal of Impact Engineering, 2021, 148: 103762. DOI: 10.1016/j.ijimpeng.2020.103762.
[15]	朱擎, 李述涛, 陈叶青. 配筋对超高性能混凝土抗侵彻性能的影响 [J]. 工程力学, 2023, 40(S1): 62–73,91. DOI: 10.6052/j.issn.1000-4750.2022.05.S046. ZHU Q, LI S T, CHEN Y Q. Influence of reinforcement on anti-penetration resistance of ultra-high-performance concrete [J]. Engineering Mechanics, 2023, 40(S1): 62–73,91. DOI: 10.6052/j.issn.1000-4750.2022.05.S046.
[16]	张爽, 武海军, 黄风雷. 刚性弹正侵彻钢筋混凝土靶阻力模型 [J]. 兵工学报, 2017, 38(11): 2081–2092. DOI: 10.3969/j.issn.1000-1093.2017.11.001. ZHANG S, WU H J, HUANG F L. Resistance model of rigid projectile penetrating into reinforced concrete target [J]. Acta Armamentarii, 2017, 38(11): 2081–2092. DOI: 10.3969/j.issn.1000-1093.2017.11.001.
[17]	黄民荣, 顾晓辉, 高永宏. 刚性弹丸侵彻钢筋混凝土的实验和简化分析模型 [J]. 实验力学, 2009, 24(4): 283–290. HUANG M R, GU X H, GAO Y H. Experiment and simplified analytical model for penetration of rigid projectile in a reinforced concrete target [J]. Journal of Experimental Mechanics, 2009, 24(4): 283–290.
[18]	黄民荣. 刚性弹体对混凝土靶的侵彻与贯穿机理研究 [D]. 南京: 南京理工大学, 2011. HUANG M R. Penetration and perforation mechanism of rigid projectile into the concrete target [D]. Nanjing: Nanjing University of Science & Technology, 2011.
[19]	HUANG C L, WANG Z Q, LI S T, et al. Analytical model of penetration depth and energy dissipation considering impact position [J]. International Journal of Impact Engineering, 2024, 191: 104997. DOI: 10.1016/j.ijimpeng.2024.104997.
[20]	刘志林, 孙巍巍, 王晓鸣, 等. 卵形弹丸垂直侵彻钢筋混凝土靶的工程解析模型 [J]. 弹道学报, 2015, 27(3): 84–90. DOI: 10.3969/j.issn.1004-499X.2015.03.016. LIU Z L, SUN W W, WANG X M, et al. Engineering analytical model of ogive-nose steel projectiles vertically penetrating reinforced concrete target [J]. Journal of Ballistics, 2015, 27(3): 84–90. DOI: 10.3969/j.issn.1004-499X.2015.03.016.
[21]	CHEN X W, LI Q M. Deep penetration of a non-deformable projectile with different geometrical characteristics [J]. International Journal of Impact Engineering, 2002, 27(6): 619–637. DOI: 10.1016/S0734-743X(02)00005-2.
[22]	PENG Y, WU H, FANG Q, et al. A note on the deep penetration and perforation of hard projectiles into thick targets [J]. International Journal of Impact Engineering, 2015, 85: 37–44. DOI: 10.1016/j.ijimpeng.2015.06.013.
[23]	中华人民共和国住房和城乡建设部, 国家市场监督管理总局. GB/T 50081-2019 混凝土物理力学性能试验方法标准 [S]. 北京: 中国建筑工业出版社, 2019: 145–146. Ministry of Housing and Urban-Rural Development of the People’s Republic of China, State Administration for Market Regulation. GB/T 50081-2019 Standard for test methods of concrete physical and mechanical properties [S]. Beijing: China Architecture and Building Press, 2019: 145–146.
[24]	黄晓莹, 陶俊林. 三种建筑钢筋材料高应变率下拉伸力学性能研究 [J]. 工程力学, 2016, 33(7): 184–189. DOI: 10.6052/j.issn.1000-4750.2014.12.1064. HUANG X Y, TAO J L. Tensile mechanical properties research of three construction steel bars in high strain rate [J]. Engineering Mechanics, 2016, 33(7): 184–189. DOI: 10.6052/j.issn.1000-4750.2014.12.1064.
[25]	NONAKA T. Some interaction effects in a problem of plastic beam dynamics-Part 2: analysis of a structure as a system of one degree of freedom [J]. Journal of Applied Mechanics, 1967, 34(3): 631–637. DOI: 10.1115/1.3607754.
[26]	FREW D J, HANCHAK S J, GREEN M L, et al. Penetration of concrete targets with ogive-nose steel rods [J]. International Journal of Impact Engineering, 1998, 21(6): 489–497. DOI: 10.1016/S0734-743X(98)00008-6.
[27]	FORRESTAL M J, ALTMAN B S, CARGILE J D, et al. An empirical equation for penetration depth of ogive-nose projectiles into concrete targets [J]. International Journal of Impact Engineering, 1994, 15(4): 395–405. DOI: 10.1016/0734-743X(94)80024-4.
[28]	CHEN X W, LI Q M. Deep penetration of a non-deformable projectile with different geometrical characteristics [J]. International Journal of Impact Engineering, 2002, 27(6): 619–637. DOI: 10.1016/S0734-743X(02)00005-2.
[29]	王安宝, 邓国强, 杨秀敏, 等. 一个新的通用型侵彻深度计算公式 [J]. 土木工程学报, 2021, 54(10): 36–46. DOI: 10.15951/j.tmgcxb.2021.10.004. WANG A B, DENG G Q, YANG X M, et al. A new general formula for calculating penetration depth [J]. China Civil Engineering Journal, 2021, 54(10): 36–46. DOI: 10.15951/j.tmgcxb.2021.10.004.
[30]	ZHANG X Y, WU H J, ZHANG S, et al. Projectile penetration of reinforced concrete considering the effect of steel reinforcement: Experimental study and theoretical analysis [J]. International Journal of Impact Engineering, 2020, 144: 103653. DOI: 10.1016/j.ijimpeng.2020.103653.